A brief course of computer graphics: setting normal maps in a tangent space
We got the hands to write another addition to my brief course on computer graphics. So, the topic for the next conversation is the use of normal maps . What is the main difference between using normal maps and Phong shading? The main difference in the density of the job information. To shade Phong, we used normal vectors defined at each vertex of our polygonal mesh, interpolating the normals inside the triangles. Using the same normal maps allows you to specify normals for each point on our surface, and not only occasionally, which simply dramatically affects the image detail.
In principle, in the lecture about shaders, we have already used the normal map, but only the one specified in the global coordinate system. Now the conversation will go about the tangent space . So, here are two textures, the left one is set in the global space (RGB directly turns into the XYZ vector), and the right one - in the tangent.

To use the normal specified in the tangent space, for the pixel to be drawn, we calculate the tangent reper (Darperbou). In this frame, one vector (z) is orthogonal to the surface, and the other two define a tangent plane to the surface. Then we read the normal vector from the texture, and convert its coordinates from the newly calculated reference frame to the global one. Since the normal map most often specifies only a small perturbation of the normal, the dominant color of the texture is blue.
It would seem, why such difficulties? Why not use a simple global rapper as before? Imagine that we want to animate our model. For example, I took our old friend Negro and opened his mouth to him. Obviously, the modified surface must have other normals!
')
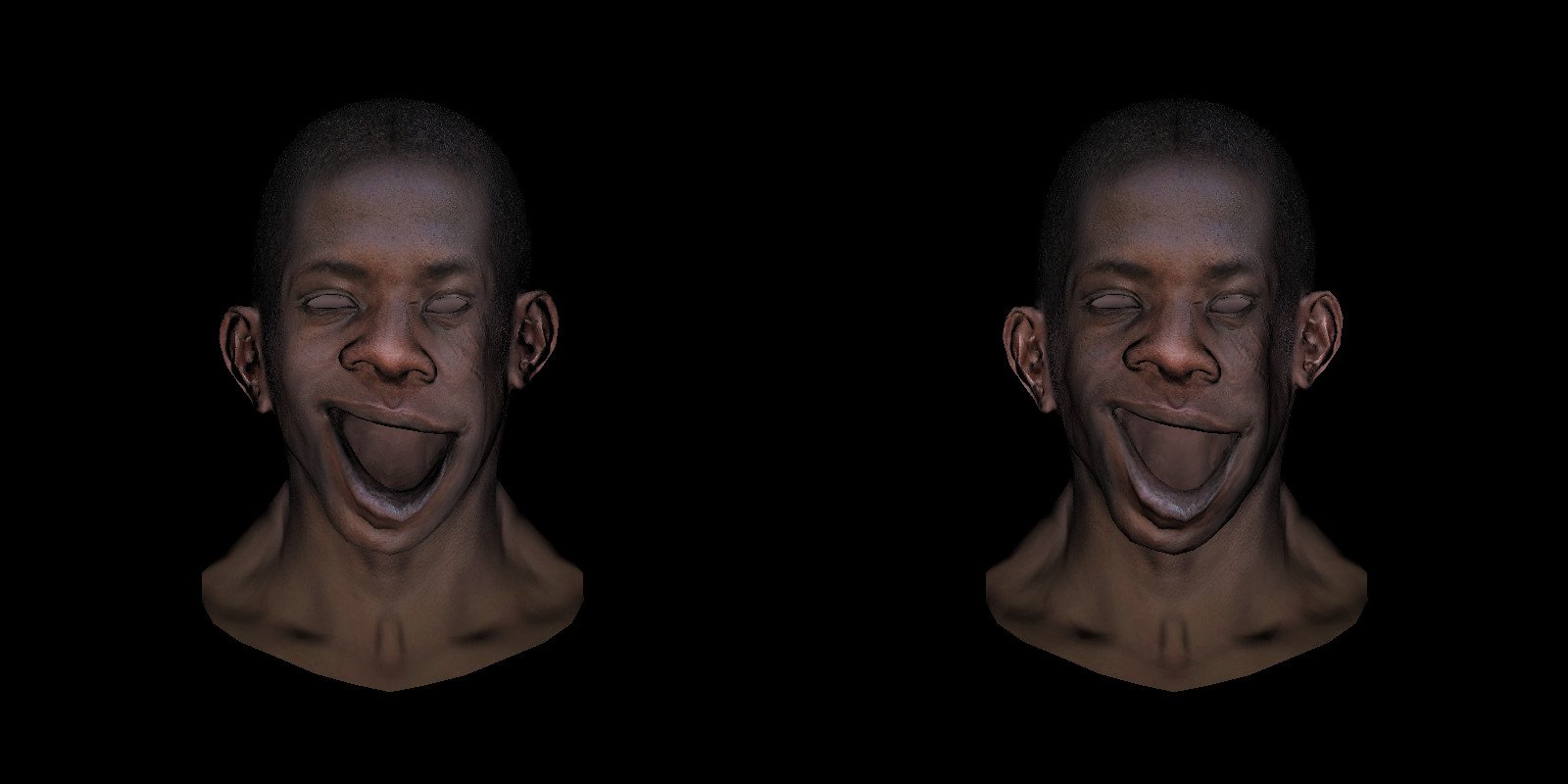
Here on the left is a model in which the mouth is open and the normal (global) map has not been changed. Look at the mucous membrane of the lower lip. The light beats right in the face, the model with the mouth closed mucous, of course, was not covered in any way. The mouth opened, but it is still not illuminated ... The right-hand picture is calculated using the normal map given in the tangent space.
So, if we have an animated model, then to set the normal map in the global space, we need one texture for each frame of the animation. And since the tangent space naturally follows the surface, such a texture is enough for us alone!
Here is a second example:

This is the texture for the Diablo model. Note that only one hand is visible on the texture. And only one half tail. The artist used the same texture for the left and right hands, and the same texture for the left and right side of the tail. (By the way, this is what prevented us from counting ambient occlusion .) And this means that in the global coordinate system I can specify normal vectors for either the left hand or the right hand. But not for two at once!
So, we end up with motivation and go directly to the calculations.
So let's look at the starting point . The shader is very simple, this is Phong shading.
Here is the result of the shader:

For ease of learning and debugging, I will remove the skin texture and apply the simplest regular mesh with horizontal red and vertical blue lines:

Let's take a look at how our Phong shader works using this image as an example:
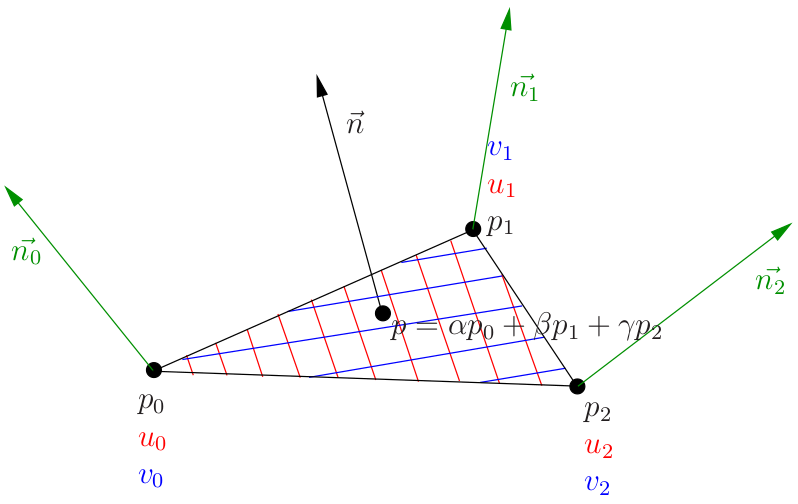
So, for each vertex of the triangle we have given its coordinates p, its textural coordinates uv and normal vectors to the vertices n. To draw each pixel, the rasterizer gives us the barycentric pixel coordinates (alpha, beta, gamma). This means that the current pixel has spatial coordinates p = alpha p0 + beta p1 + gamma p2. We interpolate the texture coordinates in exactly the same way, then interpolate the normal vector:
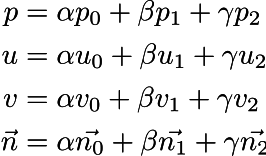
Notice that the red and blue lines are the isolines of u and v, respectively. So, for each point of our surface, we have a Darboux bench mark, whose x axis is parallel to the red lines, the y axis is parallel to the blue, and z is orthogonal to the surface. It is in this frame that the normal vectors are defined.
So, our task is for each pixel to be drawn to count the top three vectors that define the Darboux frame. Let us first distract and imagine that in our space a linear function f is defined, which assigns a real number f (x, y, z) = Ax + By + Cz + D to each point (x, y, z). The only thing we We do not know the numbers (A, B, C, D), but we know the value of the function at the vertices of a certain triangle (p0, p1, p2):
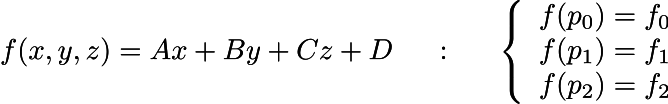
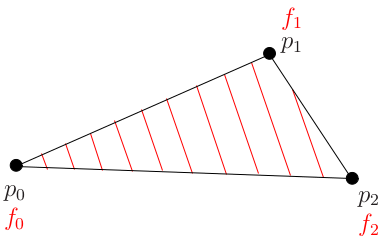
One can imagine that f is simply the height of a certain inclined plane. We fix three different points on the plane and know the values of the heights at these points. The red lines on the triangle show the isolines of height: the isoline for height f0, for height f0 + 1 meter, f0 + 2 meters, etc. For a linear function, all these isolines are obviously parallel lines.
What we are interested in is not so much the direction of the isolines as the direction, orthogonal to them. If we move along some contour line, then the height does not change (thanks, captain), if we deviate a little bit from the contour line, then the height begins to change, and the biggest change per unit height will be when we move in the direction orthogonal isolines.
We recall that the direction of the fastest lifting for some function is nothing but its gradient. For a linear function f (x, y, z) = Ax + By + Cz + D, its gradient is a constant vector (A, B, C). It is logical that it is constant, since any point of the plane is tilted equally. I remind you that we do not know the numbers (A, B, C). We only know the value of our function at three different points. Can we recover A, B and C? Of course.
So, we have three points p0, p1, p2 and three values of the function f0, f1, f2. We are interested in finding a vector (A, B, C) that gives the direction of the fastest growth of the function f. Let's consider, for convenience, the function g (p), which is given by g (p) = f (p) - f (p0):
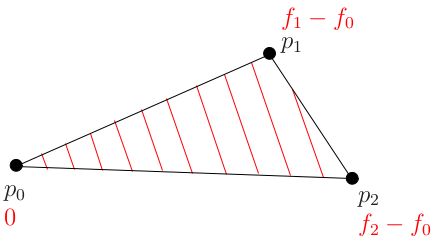
Obviously, we simply moved our inclined plane, without changing its inclination, so the direction of the fastest growth for g will coincide with the direction of the fastest growth of f.
Let's rewrite the definition of g:
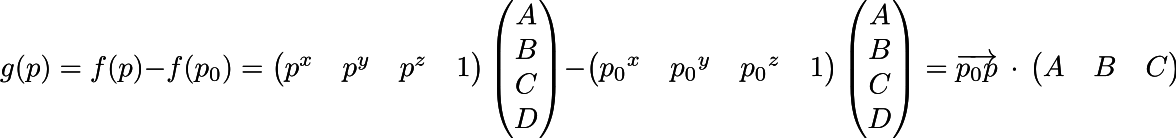
Notice that the superscript p ^ x is the x coordinate of the point p, not a power. That is, the function g is only the scalar product of the vector connecting the current point p with the point p0 and the vector (A, B, C). But we still do not know (A, B, C)! Not scary, now we find them.
So what do we know? We know that if from the point p0 we go to p2, then the function g will be equal to f2-f0. In other words, the scalar product between the vectors p2-p0 and ABC is f2-f0. The same for dot (p1-p0, ABC) = f1-f0. That is, we are looking for a vector (ABC), which is simultaneously orthogonal to the normal to the triangle and has these two restrictions on scalar products:
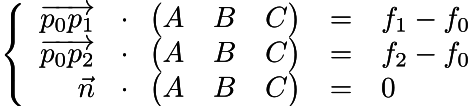
We write the same in matrix form:
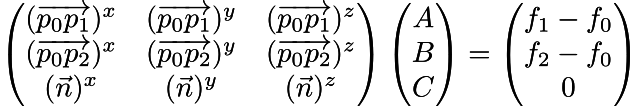
That is, we have obtained the matrix equation Ax = b, which is easily solved:
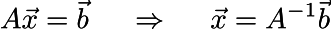
Notice that I used letter A in two ways, the meaning should be clear from the context. That is, our 3x3 matrix A multiplied by the unknown vector x = (A, B, C) gives the vector b = (f1-f0, f2-f0, 0). The unknown vector is found by multiplying the inverse of A by the vector b.
Note that there is nothing in the matrix A that depends on the function f! It contains only information about the geometry of the triangle.
Total, Darboux frame is a triplet of vectors (i, j, n), where n is the normal vector, and i and j can be calculated as follows:
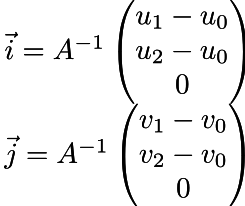
Here is the final code that uses normal maps defined in the tangent space, and here you can find changes in the code compared to Phong tinting.
Everything is pretty straightforward, I calculate the matrix A:
Then I compute Darboux vector:
Well, once I have calculated them, I read the normal from the texture, and do the simplest transformation of coordinates from the Darboux reference point into the global reference.
If that, then I already described transformations of coordinates.
Here is the final render, compare the details with Phong's tint :
It's time to remember how the lines are drawn . Overlay the model with a regular red-blue grid and for all vertices draw the resulting vectors (i, j), they should match well with the direction of the red-blue texture lines.
Happy coding!
In principle, in the lecture about shaders, we have already used the normal map, but only the one specified in the global coordinate system. Now the conversation will go about the tangent space . So, here are two textures, the left one is set in the global space (RGB directly turns into the XYZ vector), and the right one - in the tangent.

To use the normal specified in the tangent space, for the pixel to be drawn, we calculate the tangent reper (Darperbou). In this frame, one vector (z) is orthogonal to the surface, and the other two define a tangent plane to the surface. Then we read the normal vector from the texture, and convert its coordinates from the newly calculated reference frame to the global one. Since the normal map most often specifies only a small perturbation of the normal, the dominant color of the texture is blue.
It would seem, why such difficulties? Why not use a simple global rapper as before? Imagine that we want to animate our model. For example, I took our old friend Negro and opened his mouth to him. Obviously, the modified surface must have other normals!
')

Here on the left is a model in which the mouth is open and the normal (global) map has not been changed. Look at the mucous membrane of the lower lip. The light beats right in the face, the model with the mouth closed mucous, of course, was not covered in any way. The mouth opened, but it is still not illuminated ... The right-hand picture is calculated using the normal map given in the tangent space.
So, if we have an animated model, then to set the normal map in the global space, we need one texture for each frame of the animation. And since the tangent space naturally follows the surface, such a texture is enough for us alone!
Here is a second example:

This is the texture for the Diablo model. Note that only one hand is visible on the texture. And only one half tail. The artist used the same texture for the left and right hands, and the same texture for the left and right side of the tail. (By the way, this is what prevented us from counting ambient occlusion .) And this means that in the global coordinate system I can specify normal vectors for either the left hand or the right hand. But not for two at once!
So, we end up with motivation and go directly to the calculations.
Phong shading starting point
So let's look at the starting point . The shader is very simple, this is Phong shading.
struct Shader : public IShader { mat<2,3,float> varying_uv; // triangle uv coordinates, written by the vertex shader, read by the fragment shader mat<3,3,float> varying_nrm; // normal per vertex to be interpolated by FS virtual Vec4f vertex(int iface, int nthvert) { varying_uv.set_col(nthvert, model->uv(iface, nthvert)); varying_nrm.set_col(nthvert, proj<3>((Projection*ModelView).invert_transpose()*embed<4>(model->normal(iface, nthvert), 0.f))); Vec4f gl_Vertex = Projection*ModelView*embed<4>(model->vert(iface, nthvert)); varying_tri.set_col(nthvert, gl_Vertex); return gl_Vertex; } virtual bool fragment(Vec3f bar, TGAColor &color) { Vec3f bn = (varying_nrm*bar).normalize(); Vec2f uv = varying_uv*bar; float diff = std::max(0.f, bn*light_dir); color = model->diffuse(uv)*diff; return false; } }; Here is the result of the shader:

For ease of learning and debugging, I will remove the skin texture and apply the simplest regular mesh with horizontal red and vertical blue lines:

Let's take a look at how our Phong shader works using this image as an example:

So, for each vertex of the triangle we have given its coordinates p, its textural coordinates uv and normal vectors to the vertices n. To draw each pixel, the rasterizer gives us the barycentric pixel coordinates (alpha, beta, gamma). This means that the current pixel has spatial coordinates p = alpha p0 + beta p1 + gamma p2. We interpolate the texture coordinates in exactly the same way, then interpolate the normal vector:
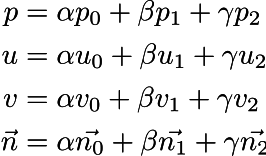
Notice that the red and blue lines are the isolines of u and v, respectively. So, for each point of our surface, we have a Darboux bench mark, whose x axis is parallel to the red lines, the y axis is parallel to the blue, and z is orthogonal to the surface. It is in this frame that the normal vectors are defined.
Calculate the linear function of its three points
So, our task is for each pixel to be drawn to count the top three vectors that define the Darboux frame. Let us first distract and imagine that in our space a linear function f is defined, which assigns a real number f (x, y, z) = Ax + By + Cz + D to each point (x, y, z). The only thing we We do not know the numbers (A, B, C, D), but we know the value of the function at the vertices of a certain triangle (p0, p1, p2):
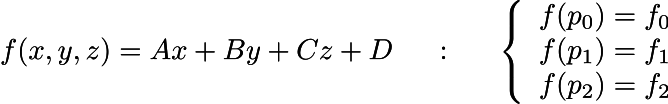

One can imagine that f is simply the height of a certain inclined plane. We fix three different points on the plane and know the values of the heights at these points. The red lines on the triangle show the isolines of height: the isoline for height f0, for height f0 + 1 meter, f0 + 2 meters, etc. For a linear function, all these isolines are obviously parallel lines.
What we are interested in is not so much the direction of the isolines as the direction, orthogonal to them. If we move along some contour line, then the height does not change (thanks, captain), if we deviate a little bit from the contour line, then the height begins to change, and the biggest change per unit height will be when we move in the direction orthogonal isolines.
We recall that the direction of the fastest lifting for some function is nothing but its gradient. For a linear function f (x, y, z) = Ax + By + Cz + D, its gradient is a constant vector (A, B, C). It is logical that it is constant, since any point of the plane is tilted equally. I remind you that we do not know the numbers (A, B, C). We only know the value of our function at three different points. Can we recover A, B and C? Of course.
So, we have three points p0, p1, p2 and three values of the function f0, f1, f2. We are interested in finding a vector (A, B, C) that gives the direction of the fastest growth of the function f. Let's consider, for convenience, the function g (p), which is given by g (p) = f (p) - f (p0):

Obviously, we simply moved our inclined plane, without changing its inclination, so the direction of the fastest growth for g will coincide with the direction of the fastest growth of f.
Let's rewrite the definition of g:
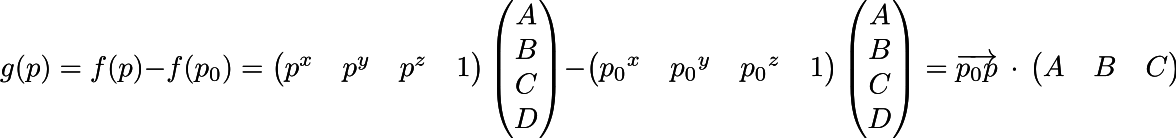
Notice that the superscript p ^ x is the x coordinate of the point p, not a power. That is, the function g is only the scalar product of the vector connecting the current point p with the point p0 and the vector (A, B, C). But we still do not know (A, B, C)! Not scary, now we find them.
So what do we know? We know that if from the point p0 we go to p2, then the function g will be equal to f2-f0. In other words, the scalar product between the vectors p2-p0 and ABC is f2-f0. The same for dot (p1-p0, ABC) = f1-f0. That is, we are looking for a vector (ABC), which is simultaneously orthogonal to the normal to the triangle and has these two restrictions on scalar products:
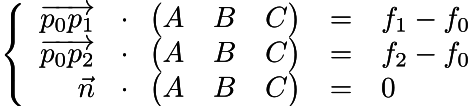
We write the same in matrix form:
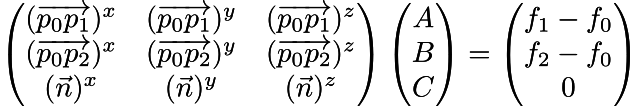
That is, we have obtained the matrix equation Ax = b, which is easily solved:
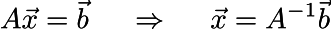
Notice that I used letter A in two ways, the meaning should be clear from the context. That is, our 3x3 matrix A multiplied by the unknown vector x = (A, B, C) gives the vector b = (f1-f0, f2-f0, 0). The unknown vector is found by multiplying the inverse of A by the vector b.
Note that there is nothing in the matrix A that depends on the function f! It contains only information about the geometry of the triangle.
We calculate the Darboux frame and apply the normal map (perturbations)
Total, Darboux frame is a triplet of vectors (i, j, n), where n is the normal vector, and i and j can be calculated as follows:
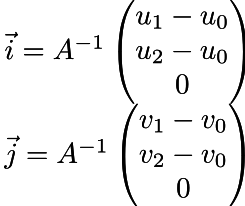
Here is the final code that uses normal maps defined in the tangent space, and here you can find changes in the code compared to Phong tinting.
Everything is pretty straightforward, I calculate the matrix A:
mat<3,3,float> A; A[0] = ndc_tri.col(1) - ndc_tri.col(0); A[1] = ndc_tri.col(2) - ndc_tri.col(0); A[2] = bn; Then I compute Darboux vector:
mat<3,3,float> AI = A.invert(); Vec3f i = AI * Vec3f(varying_uv[0][1] - varying_uv[0][0], varying_uv[0][2] - varying_uv[0][0], 0); Vec3f j = AI * Vec3f(varying_uv[1][1] - varying_uv[1][0], varying_uv[1][2] - varying_uv[1][0], 0); Well, once I have calculated them, I read the normal from the texture, and do the simplest transformation of coordinates from the Darboux reference point into the global reference.
If that, then I already described transformations of coordinates.
Here is the final render, compare the details with Phong's tint :

Debugging advice
It's time to remember how the lines are drawn . Overlay the model with a regular red-blue grid and for all vertices draw the resulting vectors (i, j), they should match well with the direction of the red-blue texture lines.
Happy coding!
How attentive were you?
Did you notice that in general the (flat) triangle has a normal vector constant, and I used the interpolated normal in the last row of the matrix A? Why did I do that?
Source: https://habr.com/ru/post/279143/
All Articles