Grid implementation for working with large tables. Part 2
In the previous part of the article , the general principle of the system was disassembled: we saw that its two main blocks are an interpolator and a numerator. We built the interaction scheme, and also fully discussed the implementation of the interpolator. In this part, we will analyze the implementation of a numerator: a reversible function that translates a set of values of key fields into a natural number (BigInteger) in such a way that the set 
less set 
from the point of view of a DBMS if and only if 
. Simply put, let's learn how to interpolate sets of values and, most interestingly, the lines:
Let us call the power of the data type the number of different values that can be represented using this type. The BIT type, for example, has a power of 2, and the type INT - 2 32 . Let the composite key data types have capacities
. Then the total number of possible combinations of the key field values of the composite key is 
. Suppose we can already calculate the functions of the numerators for the value of each of the fields, 
- ordinal value 
th field. Then the function of the numerator of the composite key can be represented through the functions of the enumerators of each of the fields as
')
It is easy to verify that 1) the value
has the greatest weight 
- the smallest, and the basic requirement for the function-numbering fulfilled, 2) 
.
Immediately note that the calculation
directly by the above formula requires 
multiplication operations, and it is better to use the analog of the Horner scheme to reduce the number of multiplications to 
with the same number of additions:
Now we need an algorithm for calculating the inverse function
. Note that the value similar to the interpretation of the number 
in the positional number system, only with a constantly changing from “digit” to “digit” basis. Correspondingly, transform the value back to the set of "numbers" is possible by the algorithm, which is a variation of the algorithm for representing a number in the number system with a given base (here value = 
, keys [i] .cardinality () = 
):
With the composite key sorted out, it remains to build numbering for the types encountered in practice.
If the length of the string is not limited, then the task of creating a numerator is impossible: between the lines 'a' and 'b' there are infinitely many lines 'aa', 'aaa', 'aaaa' ... in lexicographical order, and between any two natural numbers always a finite number of natural numbers. The mathematician will say that the orders of a set of lexicographically ordered strings and sets of natural numbers are non-isomorphic . Fortunately, in the known DBMS, an index can be built only on a string of limited length, and this fundamentally changes the situation.
If the alphabet contains
characters, the total number of lines of length not more than 
in this alphabet equals
Here, the unit corresponds to an empty string, - the number of lines of one character, 
- the number of lines of two characters, etc., and in the end it turns out the good old amount of a geometric progression.
Imagine now an arbitrary string.
lengths 
as an array 
where 
- number th symbol of a line in the alphabet (counting from zero), positions of characters in a string are also considered from zero. Then the string in simple lexicographical order will have a number
To optimize the calculation and the inverse function, you need to prepare in advance an array of coefficients
Of course, use this formula directly when storing values
no need: you can save on arithmetic operations by noticing that all are partial sums of a geometric progression that can be calculated “on the fly” when filling an array .
Algorithm to calculate the inverse function , as in the case of a composite key numerator, is a variation of the algorithm for converting a number into a number system with an arbitrary base. It is only necessary at each step to subtract the unit before receiving the next character, keeping in mind the first term in the formula for 
:
The order in which the database sorts string values is actually different from simple lexicographical and uses so-called Unicode collation rules .
When comparing strings based on these rules, the database is considered in three aspects: the character itself, its case (case), and its variant (accent). For example, the Russian letter "e" in most cases is considered as having two spellings, each of which has two registers: e, E; , . This allows for sorting, insensitive to the variant of writing (accent insensitive), not to distinguish between "e" and "", and when sorting to be case-insensitive, not to distinguish between uppercase and lowercase letters. At the same time, what is considered a separate letter, and what is a variant of writing another letter, depends on cultural traditions and may differ even in languages that use the same alphabet.
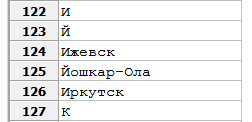
For example, if in the Russian cultural tradition there are still disagreements about the status of the letter "", then no one doubts that "and" and "d" are different letters. In the alphabetical list of cities "Yoshkar-Ola" should follow after "Irkutsk", whatever the mode of sorting. If, however, in the PostgreSQL database, you specify accent insensitive collation English-US and enter a list of cities in the table, then by sorting them by name, you may find that Yoshkar-Ola will follow “Irkutsk”, although after “Izhevsk ". The reason, of course, is that the chosen set of matching rules considers the “d” not an independent symbol, but a variant of writing the letter “and”:
The general algorithm for string comparison, taking into account matching rules, is as follows:
All these subtleties are essential for the implementation of our task, since adequate work of the grid is possible only if the values returned by the numerator increase on an increasing set (from the point of view of the database!) Set of arguments.
Thus, we, first, need to modify the algorithm of the numerator for strings so that it takes into account matching rules, and second, we need to be able to set different matching rules, “teaching” the grid to work with this or that database.
The first of these tasks is relatively simple considering the results already obtained. Any string value must not be treated as a one-dimensional array of characters. , and as an array of three-component values (vectors, if you like) 
, 
. Here 
- number th symbol in the alphabet 
- his spelling variant, 
- his own register. Then work with a string field can be done similarly to working with a composite key consisting of three fields.
If known
- the number of characters in the alphabet, 
- the maximum number of spellings and 
- the maximum number of registers (in languages known to us 
: "Uppercase" and "lowercase"), then
Where
- the formula value calculated by the first components of the line ( 
),
The inverse function is easy to build, using the principles already outlined above: first you need to divide into three components 
, 
and 
, then get an array of three-component values, on the basis of which the original string is restored.
The standard Java library has an abstract class java.text.Collator and its implementation java.text.RuleBasedCollator . The purpose of these classes is to compare strings, taking into account various matching rules. An extensive library of ready-made rules is available. Unfortunately, these classes are not suitable for use with any purpose other than string comparison: all information about matching rules is encapsulated and cannot be obtained using the system library in a regular manner.
Therefore, in order to solve our problem, it was necessary to create an interpreter of matching rules independently.
This task was facilitated by the study of the class RuleBasedCollator. The main borrowed idea was the language for defining sorting rules, a formal description of which is given in the documentation . It is easiest to understand how this language works by examining an example of a rule:
The following characters are service marks in the language of matching rules:
Using expressions like the above, you can define rules that correspond to different comparisons of different databases. Since the matching rules language is rather primitive, there was enough algorithm for parsing expressions on it that works as a deterministic finite state machine . As a result, for a given rule expression, we get an instance of a class capable of
The numerator for string values is built, you can assemble the system according to the scheme described in the first part of the article .
Already after the system was assembled and testing began, features were discovered that entailed some improvements.
First, an important nuance in the practical implementation was the need for a separate processing of the scrolling slider movement for a small step .
Scrolling one line up or down happens when you click the up and down arrows on the vertical scroll bar. When you click on the free field of the scroll bar at the top or bottom of the slider, it scrolls to a fixed (small) number of lines. In these cases, the user expects to shift all visible lines on the screen by a fixed number of positions. An interpolator that has not collected enough interpolation points may behave unpredictably, throwing the picture displayed to the user too far back or forward, and after specifying the position of the scrollbar will not correspond to what the user wanted.
In this case, however, the use of an interpolator is not justified. If you know the previous set of key field values, then you can get one previous (or one next) record by a quick query to the database. Having done this several times, it is possible to obtain several previous or subsequent recordings, still in an inconspicuous time.
After extracting this data, in addition to displaying it to the user, you can replenish the interpolation table with one more point, without resorting to a request for counting records , since the resulting record has a number that differs from the previous one by a known value.
Another important nuance in the practical implementation was the need to fill the interpolation table with data before the user starts scrolling the grid.
It is not surprising that the numbers of combinations based on the data in a real table, the distribution on the number line is very uneven. Therefore, if there are not enough points in the interpolation table, the user, having shifted the scroll bar to a certain distance, can get a strong “bounce” forward or backward after specifying the position. As a result, the real position of the data being viewed will move either much further, or, conversely, much closer than the user wanted.
Tests show that an error of 20-25% of the length of the scroll bar when positioning is psychologically permissible, but no more. Therefore, after displaying the grid, it is desirable for the user to ensure that the maximum length of the “bounce” is no more than 20–25% of the length of the scroll bar even at the very beginning of work, when statistics in the interpolation table have not yet been accumulated.
This can be done efficiently in a parallel execution thread launched after displaying the grid. This stream runs a series of refinement queries, the results of which fill up the interpolation table. The key combination value for the refinement query is selected each time as lying in the middle of the largest gap in the values of the sequence numbers of the interpolation table entries. The process is performed until the width of the maximum gap is reduced to the desired size, or until the limit on the number of iterations is reached.
The grid based on the principles presented here was implemented in Java using PostgreSQL as a DBMS. As one of the load test data sets, the KLADR database containing 1075429 street names of settlements in Russia is used, sorting is carried out according to various fields and their combinations. All the principles outlined here work. When the vertical scroll bar slider is constantly moved, a full illusion of real-time scrolling of all records is created for the user, a short time after the scrolling finishes (when the refinement is triggered and another point is added to the interpolation table), the scroll bar's slider position is refined by jumping a small distance. Positioning allows you to instantly display the necessary records and immediately set the scroll bar slider approximately, after a short time its position is also specified. As you work with the grid and accumulate interpolation points, the “bounces” become less and less noticeable:
For the work done, I am preparing a scientific publication, and you can also read the preprint of the scientific version of this article at arxiv.org .
Numerator for composite key
Let us call the power of the data type the number of different values that can be represented using this type. The BIT type, for example, has a power of 2, and the type INT - 2 32 . Let the composite key data types have capacities
')
It is easy to verify that 1) the value
Immediately note that the calculation
Now we need an algorithm for calculating the inverse function
BigInteger v = value; BigInteger[] vr; for (int i = keys.length - 1; i >= 0; i--) { vr = v.divideAndRemainder(keys[i].cardinality()); keys[i].setOrderValue(vr[1]); v = vr[0]; } Numbering for primitive data types
With the composite key sorted out, it remains to build numbering for the types encountered in practice.
- The numbering of BIT values is trivial: false - 0, true - 1.
- The numbering of INT values is slightly more complicated: an INT value (a 32-bit integer with a sign) is a number between -2147483648 and 2147483647. Thus, the numerator for the INT type is simply
. Of course, one should perform addition, having already given
to type BigInteger. Inverse function
.
- Similarly, you can build a numerator for 64-bit signed integers (you need to add 9223372036854775808).
- DOUBLE (double precision floating point) numbers, presented in IEEE 754 format, have the property that they can (with minor exceptions like NaN and ± 0) be compared as signed 64-bit integers. For example, in Java, you can get for a value of type double its 64-bit image in IEEE 754 format using the Double.doubleToLongBits method.
- Finally, DATETIME values that determine the time point with an accuracy of a millisecond can also be reduced to a 64-bit integer with a sign specifying the so-called “UNIX time”, i.e. the number of milliseconds from midnight on January 1, 1970. For example, in Java this is done using the Date.getTime () method.
- Strings ( VARCHAR ) require a separate large conversation.
Line numerator (first approximation)
If the length of the string is not limited, then the task of creating a numerator is impossible: between the lines 'a' and 'b' there are infinitely many lines 'aa', 'aaa', 'aaaa' ... in lexicographical order, and between any two natural numbers always a finite number of natural numbers. The mathematician will say that the orders of a set of lexicographically ordered strings and sets of natural numbers are non-isomorphic . Fortunately, in the known DBMS, an index can be built only on a string of limited length, and this fundamentally changes the situation.
If the alphabet contains
Here, the unit corresponds to an empty string,
Imagine now an arbitrary string.
Proof of this formula
produced naturally by induction. Indeed: if 
, the only option is an empty string with the number 0.
If a
, the empty line will have the number 0, and each single-character will have the number 
. The unit is added because when comparing strings, an empty string will be less than any single-character string: 0 - '', 1 - 'a', 2 - 'b' ...
If a
, 
, then still 0 - '', 1 - 'a'. But now between the strings' a 'and' b 'in the space of lexicographically sorted strings are all possible strings of the form' 'a' plus any string no longer than 
": 'A', 'aa', 'aaa' ..., 'aab' ...:
The number of such lines is equal to
, and finally for single-character strings
Let one more character be added to the string, while still
. The number of this symbol with the corresponding weight (equal to the number of lines of length 
). A unit is added to the first term for each additional symbol, due to the fact that the string obtained by dropping the last symbol will be less than any of the strings of a length in the lexicographical order 
.
If a
If a
The number of such lines is equal to
Let one more character be added to the string, while still
To optimize the calculation
Of course, use this formula directly when storing values
Algorithm to calculate the inverse function
for (int i = 0; i < m; i++) { r = r.subtract(BigInteger.ONE); cr = r.divideAndRemainder(q[i]); r = cr[1]; int c = cr[0].intValue(); arr[i] = c; if (r.equals(BigInteger.ZERO)) { if (i + 1 < m) arr[i + 1] = END_OF_STRING; break; } } The line numerator for matching rules
The order in which the database sorts string values is actually different from simple lexicographical and uses so-called Unicode collation rules .
When comparing strings based on these rules, the database is considered in three aspects: the character itself, its case (case), and its variant (accent). For example, the Russian letter "e" in most cases is considered as having two spellings, each of which has two registers: e, E; , . This allows for sorting, insensitive to the variant of writing (accent insensitive), not to distinguish between "e" and "", and when sorting to be case-insensitive, not to distinguish between uppercase and lowercase letters. At the same time, what is considered a separate letter, and what is a variant of writing another letter, depends on cultural traditions and may differ even in languages that use the same alphabet.
For example, if in the Russian cultural tradition there are still disagreements about the status of the letter "", then no one doubts that "and" and "d" are different letters. In the alphabetical list of cities "Yoshkar-Ola" should follow after "Irkutsk", whatever the mode of sorting. If, however, in the PostgreSQL database, you specify accent insensitive collation English-US and enter a list of cities in the table, then by sorting them by name, you may find that Yoshkar-Ola will follow “Irkutsk”, although after “Izhevsk ". The reason, of course, is that the chosen set of matching rules considers the “d” not an independent symbol, but a variant of writing the letter “and”:
The general algorithm for string comparison, taking into account matching rules, is as follows:
- Strings are compared character by character without taking into account registers and variants. If a difference is found, the result is returned (“more” or “less”).
- If the sorting is accent sensitive, the numbers of variants of each of the characters are compared. If a difference is found, the result is returned.
- If sorting is case sensitive, the registers of each of the characters are compared. If a difference is found, the result is returned.
- If the exit from the algorithm has not happened so far - the lines are equal.
All these subtleties are essential for the implementation of our task, since adequate work of the grid is possible only if the values returned by the numerator increase on an increasing set (from the point of view of the database!) Set of arguments.
Thus, we, first, need to modify the algorithm of the numerator for strings so that it takes into account matching rules, and second, we need to be able to set different matching rules, “teaching” the grid to work with this or that database.
The first of these tasks is relatively simple considering the results already obtained. Any string value must not be treated as a one-dimensional array of characters.
If known
Where
The inverse function is easy to build, using the principles already outlined above: first you need to divide
The standard Java library has an abstract class java.text.Collator and its implementation java.text.RuleBasedCollator . The purpose of these classes is to compare strings, taking into account various matching rules. An extensive library of ready-made rules is available. Unfortunately, these classes are not suitable for use with any purpose other than string comparison: all information about matching rules is encapsulated and cannot be obtained using the system library in a regular manner.
Therefore, in order to solve our problem, it was necessary to create an interpreter of matching rules independently.
This task was facilitated by the study of the class RuleBasedCollator. The main borrowed idea was the language for defining sorting rules, a formal description of which is given in the documentation . It is easiest to understand how this language works by examining an example of a rule:
<,<,<,;,<,<,<,;,<,<, The following characters are service marks in the language of matching rules:
- <- separation of characters
- ; - separation of spelling options,
- - division of registers.
Using expressions like the above, you can define rules that correspond to different comparisons of different databases. Since the matching rules language is rather primitive, there was enough algorithm for parsing expressions on it that works as a deterministic finite state machine . As a result, for a given rule expression, we get an instance of a class capable of
- by the given rules get values
- define three components by a given symbol (symbol number in the alphabet, variant number, register number),
- for a given three components to determine the symbol.
The numerator for string values is built, you can assemble the system according to the scheme described in the first part of the article .
Finishing touches
Already after the system was assembled and testing began, features were discovered that entailed some improvements.
First, an important nuance in the practical implementation was the need for a separate processing of the scrolling slider movement for a small step .
Scrolling one line up or down happens when you click the up and down arrows on the vertical scroll bar. When you click on the free field of the scroll bar at the top or bottom of the slider, it scrolls to a fixed (small) number of lines. In these cases, the user expects to shift all visible lines on the screen by a fixed number of positions. An interpolator that has not collected enough interpolation points may behave unpredictably, throwing the picture displayed to the user too far back or forward, and after specifying the position of the scrollbar will not correspond to what the user wanted.
In this case, however, the use of an interpolator is not justified. If you know the previous set of key field values, then you can get one previous (or one next) record by a quick query to the database. Having done this several times, it is possible to obtain several previous or subsequent recordings, still in an inconspicuous time.
After extracting this data, in addition to displaying it to the user, you can replenish the interpolation table with one more point, without resorting to a request for counting records , since the resulting record has a number that differs from the previous one by a known value.
Another important nuance in the practical implementation was the need to fill the interpolation table with data before the user starts scrolling the grid.
It is not surprising that the numbers of combinations
Tests show that an error of 20-25% of the length of the scroll bar when positioning is psychologically permissible, but no more. Therefore, after displaying the grid, it is desirable for the user to ensure that the maximum length of the “bounce” is no more than 20–25% of the length of the scroll bar even at the very beginning of work, when statistics in the interpolation table have not yet been accumulated.
This can be done efficiently in a parallel execution thread launched after displaying the grid. This stream runs a series of refinement queries, the results of which fill up the interpolation table. The key combination value for the refinement query is selected each time as lying in the middle of the largest gap in the values of the sequence numbers of the interpolation table entries. The process is performed until the width of the maximum gap is reduced to the desired size, or until the limit on the number of iterations is reached.
Practical implementation
The grid based on the principles presented here was implemented in Java using PostgreSQL as a DBMS. As one of the load test data sets, the KLADR database containing 1075429 street names of settlements in Russia is used, sorting is carried out according to various fields and their combinations. All the principles outlined here work. When the vertical scroll bar slider is constantly moved, a full illusion of real-time scrolling of all records is created for the user, a short time after the scrolling finishes (when the refinement is triggered and another point is added to the interpolation table), the scroll bar's slider position is refined by jumping a small distance. Positioning allows you to instantly display the necessary records and immediately set the scroll bar slider approximately, after a short time its position is also specified. As you work with the grid and accumulate interpolation points, the “bounces” become less and less noticeable:
***
For the work done, I am preparing a scientific publication, and you can also read the preprint of the scientific version of this article at arxiv.org .
Source: https://habr.com/ru/post/279083/
All Articles