Superscalar Stacking Processor: We Cross Horror And Hedgehog

In this article, we will develop a (software) model of a superscalar processor with OOO and a stack machine front end .

In fact, continuation 1 & 2 .

Introduction

Why stack machine ?
Philip Kupman writes : “From a theoretical point of view, the stack is important in itself, since it is the main and most natural mechanism for executing well-structured code ... stack machines are much more efficient than register processors when working with code that has high modularity. In addition, they are very simple and demonstrate excellent performance with rather modest iron requirements. ”

The advantages of stack machines include compact code, easy compilation and interpretation of code, as well as compact state of the processor.

Successful samples of computers with stack architecture can be called Burroughs B5000 (1961 ... 1986) and HP3000 (1974 ... 2006). Do not forget about the Soviet Elbrus .
')
So why are stack machines currently pushed out by register processors to the verge of progress? The reasons, it seems, are as follows:

There are two "extreme" implementations of stack processors: with a fixed hardware stack and a stack located in memory. Both of these extremes have significant flaws: in the case of a fixed-size stack, we have problems with the compiler and / or the operating system, which must think about what will happen if the stack overflows or becomes empty and how to work out the corresponding interrupt. If there is no interrupt handling, we are dealing with a microcontroller that is doomed to be manually programmable. With such an interrupt handler, the hardware stack plays the role of a “window” to fast-access memory, while shifting this “window” is a rather expensive procedure. As a result, we have unpredictable program behavior that does not allow the use of such a processor, for example, in real-time systems, although, from the point of view of Koopman, this is just an ecological niche of such processors.
In the case of a stack that is located entirely in memory, we pay memory access for almost every instruction executed. Thus, the overall system performance is limited on top by the memory bandwidth.
The complexity of the processor has long ceased to be a deterrent to development.
The hardware implemented stack implies a strict sequence of events, and, consequently, the impossibility of using implicit program parallelism. If superscalar processors themselves distribute instructions to pipelines according to available resources, and VLIW processors expect that this work has already been done for them by the compiler, then for stack machines, an attempt to find hidden parallelism in the code faces almost insurmountable difficulties. In other words, we are again confronted with a situation where technology can provide more than the architecture can afford. What is strange.
Programming for register machines is more “technologically”. With only a few general-purpose registers, "manually" you can easily create code that will access memory only when this cannot really be avoided. Note that in the case of a stack machine, this is much more difficult to achieve. And, although the optimal distribution of temporary variables in registers is an NP-complete problem, there are several inexpensive, but effective heuristics that allow you to create quite a decent code in a reasonable time.

There were, of course, attempts to hide the register machine inside the stack wrapper, for example, Ignite or ICL2900 , but they did not have commercial success, because in fact, only for the sake of compilation convenience, users had to incur fixed costs at runtime.

So why does the author again raise this topic, which makes him think that there are prospects in this area, what problems he is trying to solve by what means?

Motives

Nobody argues with the fact that the code for stack machines is much more compact in comparison with register architectures. You can dispute the significance of this compactness, but the fact remains. How is code compression achieved? After all, it is functionally doing the same thing, what is the focus?

Consider a simple example, the calculation of the expression x + y * z + u.
When building a parse tree with a compiler, it looks like this:

The assembly code (x86) for this expression looks like this:

mov eax,dword ptr [y] imul eax,dword ptr [z] mov ecx,dword ptr [x] add ecx,eax mov eax,ecx add eax,dword ptr [u]

For a hypothetical stack engine, pseudocode is:

  push x push y push z multiply add push u add

The difference is clear and obvious, in addition to the 4 memory accesses, addition and multiplication, there are register identifiers in each instruction of the register processor.

But after all, these registers in reality do not even exist, it is a fiction that the super-scalar processor uses to denote the connection between instructions.
A set of registers and operations with them form the architecture of the processor and (at least for x86) historically formed at a time when super-scalar processors did not exist, and the names of registers meant quite physical registers.

As you know, during the time the dog could grow up and register identifiers are currently used for other purposes. The architecture now is rather an interface between the compiler and the processor. The compiler does not know how the processor actually works, and can produce code for a whole heap of compatible devices. And processors can focus on useful and important things, creating externally compatible products.

What is the fee for such a unification?

From the point of view of a super-scalar processor. Here, for example, an article from Intel, literally:
The superscalar parallelizes the sequential code. But this parallelization process is too laborious even for the current processing power, and it is this that limits the performance of the machine. It is impossible to make this conversion faster than a certain number of teams per clock. More can be done, but at the same time clocks will drop - this approach is obviously meaningless.
Here is another favorite:
The trouble is not in the superscalar itself, but in the presentation of the programs. Programs are presented sequentially, and they need to be converted into parallel execution at runtime. The main problem of the superscalar is in the unsuitability of the input code to its needs. There is a parallel algorithm of the kernel and parallel organized hardware. However, between them, in the middle, there is a certain bureaucratic organization - a consistent system of commands
From the point of view of the compiler. From the same place:
The compiler converts a program to a sequential instruction set; the overall speed of the process will depend on the sequence in which it does it. But the compiler does not know exactly how the machine works. Therefore, generally speaking, the work of the compiler today is shamanism.
The compiler makes titanic efforts to cram a program into a specified number of registers, and this number is fictitious. The compiler tries to push all the parallelism detected in the program (like a rope in the eye of a needle ) through the limitations of the architecture. To a large extent unsuccessfully.

What to do?

The problem is indicated - inconsistency of the interface / architecture with modern requirements.
What are these (new) requirements?

All concurrency known to the compiler must be transferred without loss.
The cost of unpacking dependencies between instructions should be minimal.

Again, consider the example of compiling the expression x + y * z + u.

x86	stack machine
mov eax, dword ptr [y] imul eax, dword ptr [z] mov ecx, dword ptr [x] add ecx, eax mov eax, ecx add eax, dword ptr [u]	push x push y push z multiply add push u add

The x86 registers are intended to indicate the relationship between the various instructions. And what about the stack machine, how are these dependencies implemented there? Implicitly, through the position in the stack. Each instruction knows the number of its arguments and expects to find them at the top of the stack before execution.

But what if, when we talk about the top of the stack, this is not necessarily a stack of data , but rather a stack of operations ( micro-operations , mops).

The stack instructions come from outside, but the processor is actually a register one, it can only execute quite traditional 'add r1 r2 r3'. These are the 'add ...' we call mopami. If anything, mop is a universal preform for the internal instructions of a register processor.
The processor has a pool of mops, initially they are all free, access is by index.
The mop has related information, the links are the numbers of the parent mop, the number of ancestors, ...
So, the first instruction is 'push x' (x in this case is the address), the decoder translates it into 'lload R ?, 0x .....', this mop has no input arguments, only output.
The mop is taken from the pool of free, when the free mop ends, the decoder suspends the operation.
At first this is 'lload R ?, 0x .....' register not defined.
This is our “lload R ?, 0x .....” we put on top of the stack of mop indexes.
Next come 'push y; push z' with them we do the same. Now there are three downloads in the mop stack.
Next is' multiply ', for her decoder does mop' lmul R? R? R?
Since the decoder knows that 2 instructions are needed for this instruction, it takes (and deletes) the top two mops from the top of the stack and links it to the given one. After that the index of the mop 'multiply' is entered on the top of the stack.
Next comes the 'add' with it all the same, just one argument - loading from memory, the second - multiplication.
When the mop index is out of the stack, you can try to execute it. The first one is 'push x', which is now 'lload R ?, 0x .....'
For the output argument, take the first register (R1, for example) and mark it as busy. Since this mop is not waiting for anyone, it can be put in the pipeline for execution.
After this mop is completed, we notify the heir (only one, the same tree), if any, while it determines the number of the argument register and decreases the counter of the parent mops.
If the input arguments hold the register (s), they (the register (s)) can be freed
If the counter of expected mops (at the child mop) has become equal to 0, then this mop can also be shifted to the appropriate conveyor.
...

What are the types of mops?

Operations with registers, for example, addition: the values of two registers are summed and placed in the third. These mops are binary - before being placed on the stack, the links to the two top mops are removed from the stack and the link to the given one is entered. And also unary - change of a sign, for example. When creating such an operation, its reference replaces the reference at the top of the stack.
Memory operations - loading a value from memory into a register and vice versa. A load from memory has no predecessors and is simply pushed onto the stack of the mops. Unloading into memory removes one item from the stack. Loading from memory adds a link to the stack.
The special operation is pop, it is just an instruction to the decoder to remove an element from the top of the stack.
Other - branching, function calls, service, until we consider

For operations with memory, there is a special type of communication between the mops - through the address, for example, we load the value into memory and immediately read it from memory into the register. Formally, between these operations there is no connection through the register, in fact it is. In other words, it would be nice to wait until the end of the recording before reading. Therefore, for mops in the decoder cache, it is necessary to track such dependencies. Outside the cache, this problem is solved by serialization through the memory access bus.

Software model

Speculative constructions work fine up to the point of attempting to implement them. So in the future we will be theorizing in parallel with checking on the model.

The author has implemented a simple C subset compiler sufficient for the execution of the Ackermann function. The compiler produces code for the stack machine and immediately tries to execute it on the fly.

Let's not hurry and practice on something simple, for example

  long d1, d2, d3, d4, d5, d6, d7, d8; d1 = 1; d2 = 2; d3 = 3; d4 = 4; d5 = 5; d6 = 6; d7 = 7; d8 = 8; print_long (((d1 + d2)+(d3 + d4))+((d5 + d6)+(d7 + d8))); //

But first it is necessary to determine the parameters of the processor model.

32 integer registers
4 instructions per clock are decoded
one pipeline for working with memory, loading and unloading the word to / from the register takes 3 cycles
2 pipelines with ALU , the operation of summation / subtraction takes 3 cycles, comparison - 1 cycle

Here and below, instructions are shown at the time of the end of their execution (when the registers are already defined) in the pipeline where they were executed:

tact	conv. of memory	conv. N1	conv. N2
3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 32 35	LLOAD r3 LLOAD r2 LLOAD r1 Lload r0 LLOAD r7 LLOAD r6 LLOAD r5 LLOAD r4 LSTORE r3 LSTORE r2 LSTORE r1 LSTORE r0 LSTORE r7 LSTORE r6 LSTORE r5 LSTORE r4 LLOAD r11 LLOAD r10 LLOAD r8 LLOAD r15 Lload r12 LLOAD r19 LLOAD r17 LLOAD r16	LADD r11 r10 -> r9 LADD r8 r15 -> r14 LADD r12 r19 -> r18 LADD r9 r14 -> r13 LADD r17 r16 -> r23 LADD r18 r23 -> r22 LADD r13 r22 -> r21

And in register 21, at 35, we get the cherished value of 36.

The data from the same table, but in the form of a mop dependency diagram, in brackets [] is the number of the mop completion cycle (x & y does not make sense here, only the direction of the arrows is important).

What do we see?

first 8 LLOAD instructions - loading constants
further 8 LSTORE - variable initialization by constants. It may seem strange that they were serialized in this way, because initially (LOAD & STORE) were mixed. But it is worth remembering that loading a constant from memory goes 3 cycles, 4 instructions per cycle. While the first constant is waiting for the load, the LSTORE operations, by virtue of their dependence, were in the pipeline behind LLOAD. Ltd. in action , by the way.
It seems strange that having 2 pipelines and obvious parallelism we could not load both pipelines. On the other hand, the last memory load ended after 26 cycles (8 * 3 + 2). The expression tree has a depth of three strokes per step. In total, 26 + 9 = 35 cycles, it is impossible to calculate this in principle faster. Those. To calculate this code in the fastest way, one integer pipeline is sufficient.

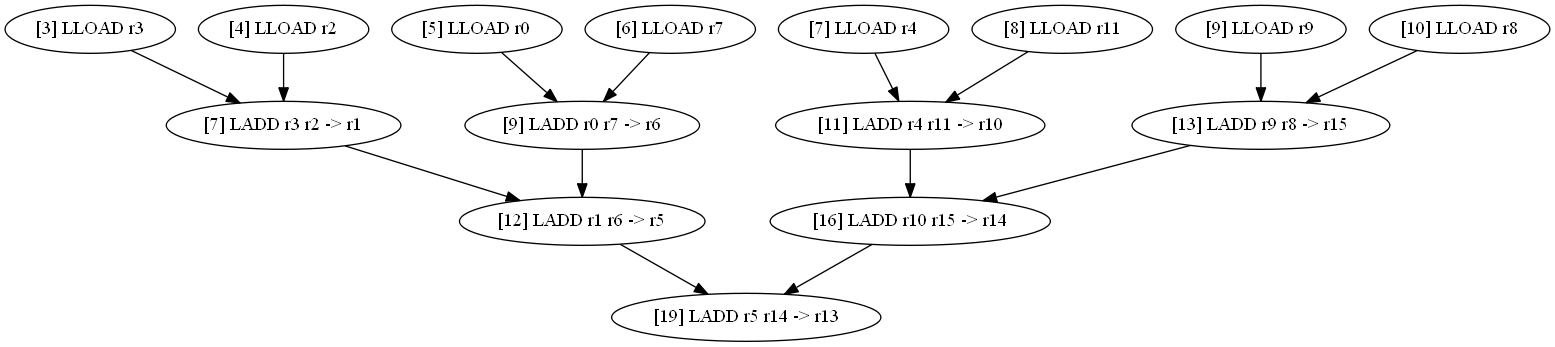
Let's try the same, but without explicit initialization of variables.

  long d1, d2, d3, d4, d5, d6, d7, d8; print_long (((d1 + d2)+(d3 + d4))+((d5 + d6)+(d7 + d8))); //

tact	conv. of memory	conv. N1	conv. N2
3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen	LLOAD r3 LLOAD r2 Lload r0 LLOAD r7 LLOAD r4 LLOAD r11 LLOAD r9 LLOAD r8	LADD r3 r2 -> r1 LADD r0 r7 -> r6 LADD r4 r11 -> r10 LADD r1 r6 -> r5 LADD r9 r8 -> r15 LADD r10 r15 -> r14 LADD r5 r14 -> r13

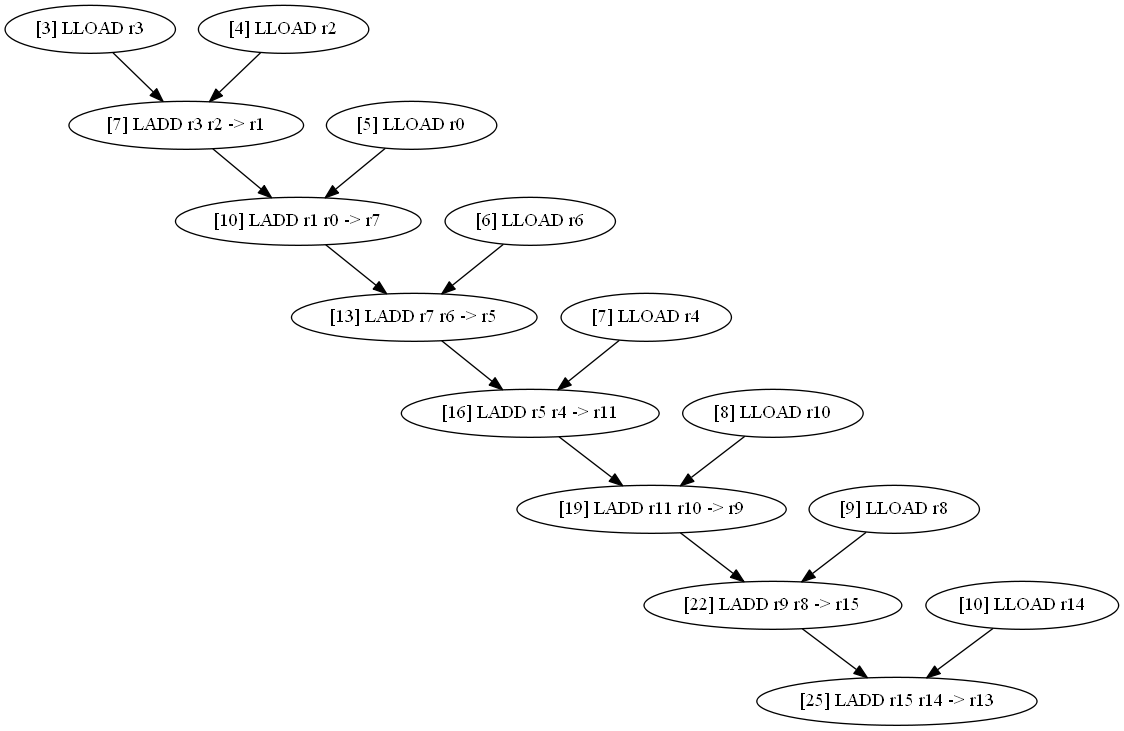
The calculation took 8 + 2 + 3 * 3 = 19 cycles, the minimum of the possible, again one pipeline was enough.

Now we will try to remove all the brackets and just sum up the variables.

  long d1, d2, d3, d4, d5, d6, d7, d8; print_long (d1+d2+d3+d4+d5+d6+d7+d8); //

tact	conv. of memory	conv. N1	conv. N2
3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 22 23 24 25	LLOAD r3 LLOAD r2 Lload r0 LLOAD r6 LLOAD r4 LLOAD r10 LLOAD r8 LLOAD r14	LADD r3 r2 -> r1 LADD r1 r0 -> r7 LADD r7 r6 -> r5 LADD r5 r4 -> r11 LADD r11 r10 -> r9 LADD r9 r8 -> r15 LADD r15 r14 -> r13

In this case, there is a data dependency and the inability to fully load the conveyor led to an extra 6 bars.

How about turning the expression inside out?

  long d1, d2, d3, d4, d5, d6, d7, d8; print_long (d1+(d2+(d3+(d4+(d5+(d6+(d7+d8))))))); //

It was worth the extra clock since data loading is not in the optimal order.

It is strange that in the presence of explicit concurrency and two integer pipelines, the second one is idle. Let's try to move the system. Let's go back to

  long d1, d2, d3, d4, d5, d6, d7, d8; print_long (((d1 + d2)+(d3 + d4))+((d5 + d6)+(d7 + d8))); //

Let's try to increase the speed of access to memory, let the reading into the register occur in 1 clock cycle. Funny, but little has changed. The total time decreased by 2 clocks, more precisely, the whole picture moved up by 2 clocks. It is understandable, the memory bandwidth has not changed, we just removed the delay to obtain the first result.

Perhaps the summation is going too fast. Let it be done 7 cycles instead of 3.
The total time increased to 29 (8 + 3 * 7) cycles, but in principle nothing has changed, the second pipeline is idle.

Let's try to sum up the pyramid of 16 numbers and enter 2 memory pipelines. The total time is 36 cycles (16/2 + 4 * 7). The second numeric pipeline was not involved. Numbers now come in pairs, all 8 summations of the first level start with a delay in tact and this is enough for everything to fit into one conveyor.

And only if you enter 4 memory pipelines and allow 6 decoding per clock, it comes to the second numeric pipeline (it has already executed 3 (sic!) Instructions), however, the total time is 33 clock cycles. Those. the effectiveness of the summation itself has even deteriorated.

Indeed, the conveyor is a very effective mechanism and we need quite weighty arguments to have more than one.

Register allocation

In the examples described above, the assignment of registers took place at the time of creation of the mops. As a result, the register usage map when summing variables with a pyramid looks like this (initial parameters - 4 instructions are decoded per cycle, one memory pipeline, three clocks for reading and summing):

8 variables	16 variables

If, on the other hand, you assign registers at the time the instructions are placed in the pipeline, the picture looks much better:

8 variables	16 variables

For the control, it is worthwhile to give the instruction dependency diagram (8 numbers):

Function call

From general considerations, the architecture being described has problems calling functions. In fact, after returning from a function, we expect a return of the state of the registers in the context of the current function. In modern register architectures for this, registers are divided into two categories — the caller is responsible for the safety of some, the callee for others.

But in our front-end stack architecture, therefore, the compiler may not be aware of the existence of any kind of registers. And the processor itself should take care of saving / restoring the context, which seems to be a non-trivial task.

However, we will solve this problem in the next article .

Source: https://habr.com/ru/post/278575/

All Articles