Image binarization: Bradley algorithm
I want to dedicate this post to a pleasant trophy, obtained in the English-speaking Internet. It will be a question of one of the methods of adaptive binarization of images, the Bradley method (or Bradley-Roth, since there are two authors).
The process of binarization is the translation of a color (or in grayscale) image into a two-color black and white. The main parameter of this transformation is the threshold t - the value with which the brightness of each pixel is compared. According to the results of the comparison, the pixel is assigned the value 0 or 1. There are various binarization methods that can be divided into two groups - global and local. In the first case, the threshold value remains unchanged during the entire binarization process. In the second, the image is divided into regions, in each of which a local threshold is calculated.
The main goal of binarization is a radical reduction in the amount of information with which to work. Simply put, successful binarization greatly simplifies the subsequent work with the image. On the other hand, failures in the binarization process can cause distortions, such as line breaks, loss of significant details, loss of integrity of objects, noise, and unpredictable distortion of characters due to background heterogeneity. Different binarization methods have their weak points: for example, the Otsu method can lead to the loss of small details and the "sticking together" of nearby symbols, and the Niblack method sins with the appearance of false objects in the case of background heterogeneities with low contrast. It follows that each method must be applied in its own field.
At the moment I am engaged in the recognition of the indications of household appliances in the framework of the popular idea of "smart home". Here is an example of the image that our group works with:
')

The photo was taken on a dark, dark night in a dark, dark room; LED illumination on the side creates a highly heterogeneous background, and between the camera and the display of the device there is silicate glass, which creates additional noise and false formations in the background. Our task is to prepare the image for text recognition.
Here it is logical to use local methods, they are also adaptive. The Niblack method is considered to be the fastest of the classical local algorithms, but it does not work well with low-contrast background asperities, which in our case fill the image slightly less than completely. To correct this deficiency, smart people have developed several modifications of the Niblack method, called “Niblack”. In my case, one of them, the Christian method, showed good results on most samples, and was almost adopted as a working option. However, distortions appeared on other samples after applying this algorithm.

a) Niblack method b) Christian method
In itself, the comparison of two values - the threshold and brightness of a pixel - is an elementary task. Not in this salt. The difficulty lies in finding the threshold value, which should reliably separate the characters not only from the background, but also from noise, shadows, highlights and other information garbage. Often for this resort to methods of mathematical statistics. In the Bradley method, we go from the other side - from the side of integral images.
Integral images are not only effective and fast (in just one pass through the image) a way to find the sum of pixel values, but also an easy way to find the average brightness value within a given image area.
How it works? Yes, elementary. Suppose we have an 8-bit image in shades of gray (a color image can be converted to shades of gray using the formula I = 0.2125R + 0.7154G + 0.0721B). In this case, the value of the element of the integral image is calculated by the formula:
S (x, y) = I (x, y) + S (x-1, y) + S (x, y-1) - S (x-1, y-1);
where S is the result of previous iterations for a given pixel position, I is the brightness of the pixel of the original image. If the coordinates are outside the image, they are considered to be zero. The essence of this method "on the fingers" is presented in the diagram below:
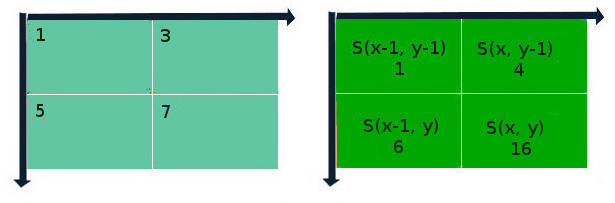
Life hacking consists in the fact that once having made an integral matrix of an image, you can quickly calculate the sum of the pixel values of any rectangular area within that image. Let ABCD be a rectangular area of interest.
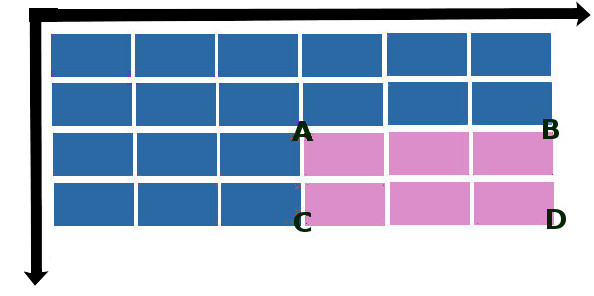
Then the total brightness S in this area is calculated by the formula:
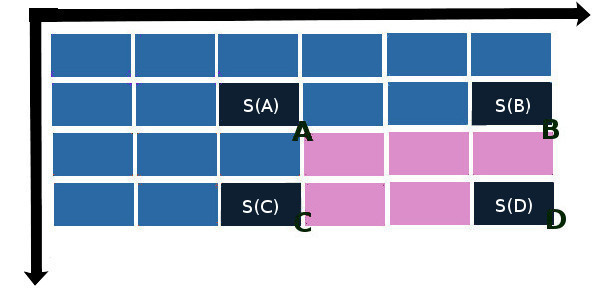
S (x, y) = S (A) + S (D) - S (B) - S ©
where S (A), S (B), S and S (D) are the values of the elements of the integral matrix in the direction “north-west” from the intersections of the sides of the rectangle:
If you have read this far, you have almost understood the Bradley algorithm. Then everything is simple. We divide the image into several areas with side d, take the average of the sum of the pixels Im in this area, add some value t, compare the value of each pixel with the result. Im + t - is our desired threshold value. Bradley and Roth take d and t values, respectively, 1/8 of the image width and 15% of the average pixel brightness value over the region. Well, generally speaking, both of these parameters can and should be changed in accordance with the specific situation. So, if the object's dimensions are larger than the square of a square with a side equal to d, then the center of this object can be taken by the algorithm as a background, and the problem is solved by reducing the value of d, however, fine details of the image can be lost.
And this is how it looks in our example:

After median filtering:

The implementation of the Bradley-Roth algorithm in C ++ is presented below:
The advantages of the Bradley-Roth method are the ease of implementation and high speed of execution; for most cases, there is no need to select parameters. The method works well with a non-uniform background.
From the latter virtue, there is a logical lack of the Bradley method, namely, the poor sensitivity to low-contrast details of the image:
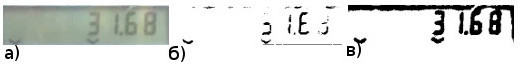
a) the original image b) the Bradley method c) the method of Christian
References:
http://citeseerx.ist.psu.edu - original article by Bradley and Roth (in English)
https://computersciencesource.wordpress.com - the author very clearly describes the essence of integral images (in English)
http://web.mit.edu/mfeng/www/papers/mengling_ieice.pdf - a review of the Niblack methods (and them too) with formulas and links to the articles of the authors (in English)
http://liris.cnrs.fr/christian.wolf/software/binarize/ - Christian Wulff implements the Christian Wolfe, Niblack and Savola algorithms (in C ++)
Some theory
The process of binarization is the translation of a color (or in grayscale) image into a two-color black and white. The main parameter of this transformation is the threshold t - the value with which the brightness of each pixel is compared. According to the results of the comparison, the pixel is assigned the value 0 or 1. There are various binarization methods that can be divided into two groups - global and local. In the first case, the threshold value remains unchanged during the entire binarization process. In the second, the image is divided into regions, in each of which a local threshold is calculated.
The main goal of binarization is a radical reduction in the amount of information with which to work. Simply put, successful binarization greatly simplifies the subsequent work with the image. On the other hand, failures in the binarization process can cause distortions, such as line breaks, loss of significant details, loss of integrity of objects, noise, and unpredictable distortion of characters due to background heterogeneity. Different binarization methods have their weak points: for example, the Otsu method can lead to the loss of small details and the "sticking together" of nearby symbols, and the Niblack method sins with the appearance of false objects in the case of background heterogeneities with low contrast. It follows that each method must be applied in its own field.
Test object
At the moment I am engaged in the recognition of the indications of household appliances in the framework of the popular idea of "smart home". Here is an example of the image that our group works with:
')

The photo was taken on a dark, dark night in a dark, dark room; LED illumination on the side creates a highly heterogeneous background, and between the camera and the display of the device there is silicate glass, which creates additional noise and false formations in the background. Our task is to prepare the image for text recognition.
Here it is logical to use local methods, they are also adaptive. The Niblack method is considered to be the fastest of the classical local algorithms, but it does not work well with low-contrast background asperities, which in our case fill the image slightly less than completely. To correct this deficiency, smart people have developed several modifications of the Niblack method, called “Niblack”. In my case, one of them, the Christian method, showed good results on most samples, and was almost adopted as a working option. However, distortions appeared on other samples after applying this algorithm.

a) Niblack method b) Christian method
The essence of the Bradley method
In itself, the comparison of two values - the threshold and brightness of a pixel - is an elementary task. Not in this salt. The difficulty lies in finding the threshold value, which should reliably separate the characters not only from the background, but also from noise, shadows, highlights and other information garbage. Often for this resort to methods of mathematical statistics. In the Bradley method, we go from the other side - from the side of integral images.
Integral images
Integral images are not only effective and fast (in just one pass through the image) a way to find the sum of pixel values, but also an easy way to find the average brightness value within a given image area.
How it works? Yes, elementary. Suppose we have an 8-bit image in shades of gray (a color image can be converted to shades of gray using the formula I = 0.2125R + 0.7154G + 0.0721B). In this case, the value of the element of the integral image is calculated by the formula:
S (x, y) = I (x, y) + S (x-1, y) + S (x, y-1) - S (x-1, y-1);
where S is the result of previous iterations for a given pixel position, I is the brightness of the pixel of the original image. If the coordinates are outside the image, they are considered to be zero. The essence of this method "on the fingers" is presented in the diagram below:

Life hacking consists in the fact that once having made an integral matrix of an image, you can quickly calculate the sum of the pixel values of any rectangular area within that image. Let ABCD be a rectangular area of interest.

Then the total brightness S in this area is calculated by the formula:
S (x, y) = S (A) + S (D) - S (B) - S ©
where S (A), S (B), S and S (D) are the values of the elements of the integral matrix in the direction “north-west” from the intersections of the sides of the rectangle:

Implementation
If you have read this far, you have almost understood the Bradley algorithm. Then everything is simple. We divide the image into several areas with side d, take the average of the sum of the pixels Im in this area, add some value t, compare the value of each pixel with the result. Im + t - is our desired threshold value. Bradley and Roth take d and t values, respectively, 1/8 of the image width and 15% of the average pixel brightness value over the region. Well, generally speaking, both of these parameters can and should be changed in accordance with the specific situation. So, if the object's dimensions are larger than the square of a square with a side equal to d, then the center of this object can be taken by the algorithm as a background, and the problem is solved by reducing the value of d, however, fine details of the image can be lost.
And this is how it looks in our example:

After median filtering:

The implementation of the Bradley-Roth algorithm in C ++ is presented below:
void Bradley_threshold(unsigned char* src, unsigned char* res, int width, int height) { const int S = width/8; int s2 = S/2; const float t = 0.15; unsigned long* integral_image = 0; long sum=0; int count=0; int index; int x1, y1, x2, y2; // integral_image = new unsigned long [width*height*sizeof(unsigned long*)]; for (int i = 0; i < width; i++) { sum = 0; for (int j = 0; j < height; j++) { index = j * width + i; sum += src[index]; if (i==0) integral_image[index] = sum; else integral_image[index] = integral_image[index-1] + sum; } } // for (int i = 0; i < width; i++) { for (int j = 0; j < height; j++) { index = j * width + i; x1=i-s2; x2=i+s2; y1=j-s2; y2=j+s2; if (x1 < 0) x1 = 0; if (x2 >= width) x2 = width-1; if (y1 < 0) y1 = 0; if (y2 >= height) y2 = height-1; count = (x2-x1)*(y2-y1); sum = integral_image[y2*width+x2] - integral_image[y1*width+x2] - integral_image[y2*width+x1] + integral_image[y1*width+x1]; if ((long)(src[index]*count) < (long)(sum*(1.0-t))) res[index] = 0; else res[index] = 255; } } delete[] integral_image; } Advantages and disadvantages
The advantages of the Bradley-Roth method are the ease of implementation and high speed of execution; for most cases, there is no need to select parameters. The method works well with a non-uniform background.
From the latter virtue, there is a logical lack of the Bradley method, namely, the poor sensitivity to low-contrast details of the image:
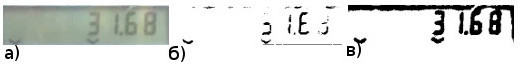
a) the original image b) the Bradley method c) the method of Christian
References:
http://citeseerx.ist.psu.edu - original article by Bradley and Roth (in English)
https://computersciencesource.wordpress.com - the author very clearly describes the essence of integral images (in English)
http://web.mit.edu/mfeng/www/papers/mengling_ieice.pdf - a review of the Niblack methods (and them too) with formulas and links to the articles of the authors (in English)
http://liris.cnrs.fr/christian.wolf/software/binarize/ - Christian Wulff implements the Christian Wolfe, Niblack and Savola algorithms (in C ++)
Source: https://habr.com/ru/post/278435/
All Articles