Euclidean algorithm for generating traditional musical rhythms
Translation of the article Godfried Toussaint The Euclidean Algorithm Generates Traditional Musical Rhythms .
In Sonic Pi, there is a spread function that takes two numeric parameters and returns a set of values for generating a rhythm. In the description of this function there is a link to the work "The Euclidean Algorithm Generates Traditional Musical Rhythms". This brilliant article, published already in 2005, seems to have not been translated into Russian. Not being a translation specialist, I tried, nevertheless, to fill this gap.
A little explanation about the word “necklace”: in the text of the article “necklace”, there is no such term in musical theory, as far as I know. I suppose that this is just some kind of visual intuition of the author, indeed, the rhythmic ring, in the form in which it is presented in the drawings, resembles a necklace - that's why I translate it.
The Euclidean algorithm (which reached us from the Euclidean Principles) calculates the greatest common divisor of two integers. This paper demonstrates that the structure of the Euclidean algorithm can be used to very effectively generate a large family of rhythms used as pulsations ( ostinato ), particularly in tropical Africa, and in traditional music in general. These rhythms, called here Euclidean rhythms, have the property that their percussion patterns are distributed as evenly as possible. Euclidean rhythms also find application in accelerators in atomic physics and computer science, and are closely related to several families of words and sequences studied by combinatorics of words, such as Euclidean strings, with which Euclidean rhythms are compared.
What is common to African rhythms, splitting neutron accelerators (S N S - spallation neutron source) in atomic physics, string theory in computer science and the ancient algorithm described by Euclidean? The short answer is: the patterns are distributed as evenly as possible. To get a longer answer, read on.
')
Mathematics and music are closely related to the times of Pythagoras. However, for the most part their interaction was in the realm of tones and scales. For historical examples of such an interaction, we will refer the reader to the excellent report by Coxeter [9]. On the other hand, the rhythm throughout the story was largely ignored. In this work, we establish certain mathematical connections between the musical rhythm and other areas of knowledge, such as atomic physics and computer science, as well as the work of another famous ancient Greek mathematician, Euclid of Alexandria.
Bjorklund examines the following problem [5], [4] in connection with the operation of some components (such as high-voltage power sources) of fissioning neutron accelerators (SNS) used in atomic physics. The time is divided into intervals (in the case of the SNS accelerator 10 seconds). At some of these intervals, the time system turns on the shutter, generating pulses for this task. For a given number of n time intervals and another number k < n is the number of pulses, the task is to distribute the pulses as uniformly as possible over these intervals. Bjorklund [5] represents this problem in the form of a binary sequence of k ones and n - k zeros, where each number denotes a time interval, and the ones denote pulses. The task then comes down to the following: build a binary sequence of n bits with k ones, so that the units are evenly distributed among the zeros. If k is divisible completely (without remainder) by n , then the solution is obvious. For example, if n = 16 and k = 4, then the solution is [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0]. The task is of interest when k and n are mutually prime numbers [23], that is, when k and n do not have common divisors other than one.
We will describe the Björklund algorithm using one of its examples. Consider a sequence with n = 13 and k = 5. Since 13 is 5 = 8, we begin by considering a sequence of 5 ones followed by 8 zeros, which can also be represented as 13 sequences of one bit:
[1 1 1 1 1 0 0 0 0 0 0 0 0]
We begin to move the zeros, placing zero after each unit, and we get five sequences of two bits, and three more zeros:
[10] [10] [10] [10] [10] [0] [0] [0]
Then we distribute the three remaining zeros in the same way, placing [0] after each sequence [10], and we get:
[100] [100] [100] [10] [10]
Now we have three sequences of three bits, and two sequences of two bits remain. Therefore, we continue in the same way, placing the sequence [10] after each sequence [100], and we get:
[10010] [10010] [100]
The process ends when the remainder contains only one sequence (in our case, the sequence [100]), or we end with zeros. The final sequence is thus the concatenation of [10010], [10010] and [100]:
[1 0 0 1 0 1 0 0 1 0 1 0 0]
Note that you can take another step and insert [100] between [10010] and [10010]. However, Björklund argues that since the sequence is cyclic, it does not matter (hence its stop rule). Bjorklund [5] proved that the final sequence can be built from the original sequence using O (n) arithmetic operations in the worst case.
One of the oldest known algorithms, described in the Euclidean Principles (ca. 300 BC) in Proposition 2 of Book VII , which today is called the Euclidean algorithm, finds the greatest common divisor of two given integers [12], [14]. The idea is very simple. The smaller of the numbers is successively subtracted from the larger until we reach zero, or we get a number that is smaller than the smaller of the two given numbers, in this case it is called the remainder. This residue is then again subtracted sequentially from a smaller number in order to obtain a new residue. This process continues until the residue is zero. For more specificity, consider the example of the numbers 5 and 8, which we used above. First, 8 is divided by 5 with a remainder of 3. Then 5 is divided by 3 with a remainder of 2. Then 3 is divided by 2 with a remainder of 1. Finally, 2 is divided by 2 with a remainder of 0. The greatest common divisor is thus 1. Although the original Euclidean algorithm used this way sequential subtraction, ordinary division will also work, and even faster. The steps of this process can be summarized by the following sequence of equations:
8 = (1) (5) + 3
5 = (1) (3) + 2
3 = (1) (2) + 1
2 = (1) (2) + 0
This algorithm can be briefly described in a recursive manner, as was done in [8]. Let m and k be initial numbers, where m> k .
EUCLID ( m, k )
1. if k = 0
2. then return m
3. else return EUCLID ( k , m mod k )
Running this algorithm with m = 8 and k = 5, we get:
EUCLID (8,5) = EUCLID (5,3) = EUCLID (3,2) = EUCLID (2,1) = EUCLID (1,0) = 1
From the description of the Euclidean algorithm it is clear that if m and k are equal to the number of zeros and ones in the binary sequence respectively (where n = m + k ), then the structure of the Euclidean algorithm is the same as the structure of the Björklund algorithm described above. Indeed, Björklund's algorithm uses division in the form of sequential subtraction, just as Euclid did in the Beginnings [12]. It is also well known that the EUCLID ( m, k ) algorithm being applied to two O (n) -bit numbers (binary sequences of length n ) will require O (n) arithmetic operations in the worst case [8].
The method of presenting musical rhythms in the form of binary sequences is widespread, where each bit is treated as a unit of time (for example, sixteenth note), and the zero bit represents silence (or nonaccented note), while the single bit represents attack (or beginning) of note [31 ]. Therefore, binary sequences generated by the Björklund algorithm as described above can be considered as one family of rhythms. Moreover, since the Björklund algorithm has the same structure as the Euclidean algorithm, we will call these rhythms Euclidean rhythms and denoted E (k, n) , where k means the number of ones, and n is the total length of the sequence (zeroes and ones). For example, E (5, 13) = [1001010010100]. The notation of zeros and ones is not ideal for representing binary rhythms, since it is difficult to visualize the positions of the beats and the length of the interimpact intervals. In music literature, the symbol 'x' is usually used for a single bit and the symbol '.' for zero bit. In this more traditional notation, the previous rhythm is written as E (5, 13) = [x .. xx. xx.].
The rhythm E (5, 13) is a cyclical rhythm with a length (size) of 13 beats. This is not the most common size in world music. Consider for contrast two common values of k and n ; namely, what is E (3, 8)? By applying the Euclidean algorithm to the corresponding sequence [1 1 1 0 0 0 0 0], the reader can easily verify that the result is the Euclidean rhythm E (3, 8) = [x .. x .. x.]. This rhythm illustrates a polygon (triangle) in Figure 1 (a), another convenient and common way of representing cyclical rhythms [31], where it is assumed that the rhythm starts at a point labeled “zero”, time moves clockwise, and the numbers by The sides of the triangle are inter-impact intervals. In fact, this is an even more compact representation of the rhythm in the form of an inter-impact duration of the interval vector [32].
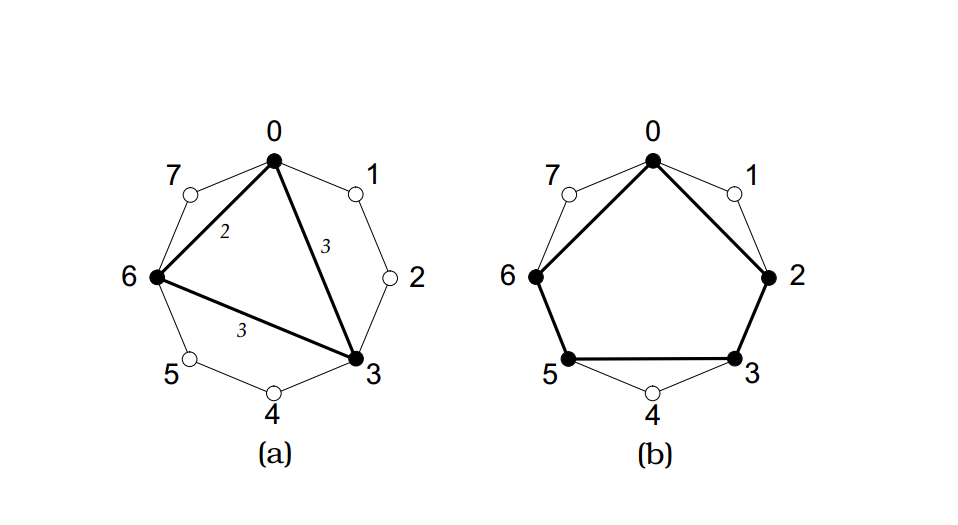
Figure 1: (a) Euclidean rhythm E (3, 8) is a Cuban tresillo , (b) Euclidean rhythm E (5, 8) is a Cuban cinquillo .
The Euclidean rhythm E (3, 8), shown in Figure 1 (a) is one of the most famous on the planet. In Cuba, it is called tresillo , and in the USA it is known as the habanera rhythm, used in hundreds of rockabilly songs throughout the 1950s. He can often be heard in early rock and roll hits in the figures in his left hand on keyboards or performed in a double bass or saxophone part [7], [15], [22]. A good example is the Elvis Presley bass rhythm. The tresillo figure is also widespread in West African folk music. For example, it is played on the atok e bell in Sohu and Ew e dances from Ghana [16]. It is also possible to recognize tresillo in the first cycle of the omnipresent clav e Son , given in the form [x .. x .. x ... xx. .].
In the two previous examples ( E (5, 13) and E (3, 8)) the number of ones is less than the number of zeros. If instead the number of ones is greater than the number of zeros, Bjorklund's algorithm gives the following steps, for example, for k = 5 and n = 8.
[1 1 1 1 1 0 0 0]
[10] [10] [10] [1] [1]
[101] [101] [10]
[1 0 1 1 0 1 1 0]
The resulting Euclidean rhythm E (5, 8) = [x. x x. xx.]. This rhythm illustrates a polygon (pentagon) in Figure 1 (b). This is another famous rhythm on the world stage. In Cuba, it is known as cinquillo and is internally related to tresillo [15]. It was used in jazz throughout the 20th century [27], as was the rockabilly music of the 1950s. For example, this is a picture of the clapping of the palm in Hound Dog by Elvis Presley [7]. The cinquillo figure is also widespread in the traditional music of West Africa [26], [31].
In the remainder of this section, we describe some of the most common Euclidean rhythms in the music of the world. In some cases, Euclidean rhythm is a reversed (rotated, formed by turning - translation ) version of the widely used rhythm. If the rhythm is a reversed version of the other, we say that both belong to the same necklace. Thus, a rhythm necklace is a model of inter-stroke durations that does not take into account the starting point of a cycle. An example of two rhythms that are instances of the same necklace is shown in Figure 2.
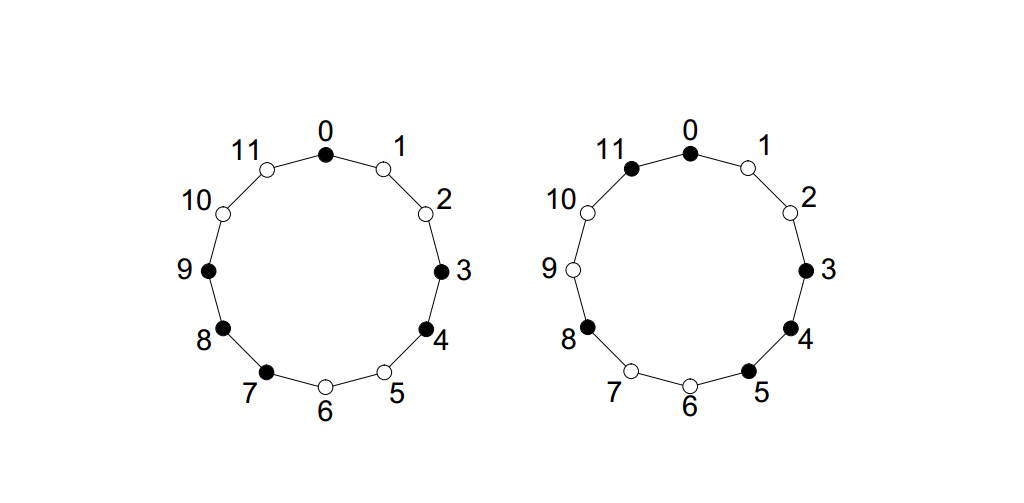
Figure 2. These two rhythms are variations of the same rhythmic necklace.
The simplest rhythms have the value k = 1. This subfamily of Euclidean rhythms gives:
E (1, 2) = [x.]
E (1, 3) = [x. .]
E (1, 4) = [x ....], Etc.
Note that since we are interested in cyclical non-periodic rhythms, there is no need to list rhythms that use the factors k and n . For example, multiplying (1, 3) by 4, we get (4, 12), which gives the rhythm:
E (4, 12) = [x .. x .. x .. x ..],
which in turn is periodic with four repetitions E (1, 3) = [x. .]. By the way, E (4, 12) = [x .. x .. x .. x. .] Is the Fandango pattern of 12/8 in flamenco music in northern Spain, where 'x' denotes a loud bang, and '.' quiet cotton [10].
E (2, 3) = [x. x] is a common Afro-Cuban percussion figure. For example, it is found in the conga rhythm in Swing Tumbao (6/8) [18]. It is also common in Latin American music, such as in Cueca [33].
E (2, 5) = [xx.] Is the thirteenth century Persian rhythm, which is called Khafif-e-ramal [34]. This is also a metric drawing of the second part of Tchaikovsky's Symphony No. 6 [17]. When it starts with a second accent ([x .. x.]), It’s the metric figure from Dave Brubeck’s Take Five , as well as from Mars in Gustav Holst’s Planets [17].
E (3, 4) = [x. xx] is the archetypical pulsation of Cumbia from Colombia [20], as well as the rhythm of Calypso from Trinidad [13]. This is also the thirteenth century Persian rhythm called Khalif-e-saghil [34], and the trochoid choreic rhythmic pattern from ancient Greece [21].
E (3, 5) = [xx x], when it starts on the second accentuated beat, is another Persian rhythm of the thirteenth century, called Khafif-e-ramal [34], as well as the rhythm of the Romanian folk dance [25].
E (3, 7) = [xxx.] Is the Ruchenitza rhythm used in the Bulgarian folk dance [24]. This is also a metric drawing in Money Pink Floyd.
E (3, 8) = [x .. x .. x.] Is the Cuban tresillo pattern, which we discussed above [15].
E (4, 7) = [xxx x] is another version of the rhythm of the Bulgarian folk dance Ruchenitza [24].
E (4, 9) = [xxxx.] Is the Turkish rhythm Aksak [6]. This is also the metric drawing used by Dave Brubeck in the play Rondo a la Turk [17].
E (4, 11) = [x .. x .. x .. x.] Is the metric figure used by Frank Zappa in his play entitled Outsid e Now [17].
E (5, 6) = [x. xxxx] gives the York-Samai pattern , a popular Arabic rhythm, when it starts on the second accentuated beat [30].
E (5, 7) = [x. x x. xx] is a Nawakhat drawing, another popular Arabic rhythm [30].
E (5, 8) = [x. x x. xx.] is the Cuban rhythm cinquillo discussed above [15]. When it begins with a second accent, it is also Spanish tango [13] and the thirteenth century Persian rhythm Al-saghilal-sani [34].
E (5.9) = [xxxx x] is the popular Arabic rhythm Agsag-Samai [30]. When it starts at the second accent, it is the drum pattern used by Venda in South Africa [26], as well as the Romanian folk dance rhythm [25].
E (5.11) = [xxxxx.] Is a metric drawing used by Mussorgsky in Pictures at an Exhibition [17].
E (5.12) = [x .. xx. x. x.] is a Venda clap from a South African children's song [24].
E (5.16) = [x .. x .. x .. x .. x ....] Is the rhythmic necklace of the Brazilian boss nova . Usually the boss-new rhythm begins on the third accentuated beat as follows: [x .. x .. x ... x .. x. .] [31]. However, there are other starting points, such as [x .. x .. x .. x ... x. .] [3].
E (7.8) = [x. xxxxxx] is a typical rhythm played on the Bendir (frame drum) and used as an accompaniment to Tuareg songs in Libya [30].
E (7.12) = [x. x xx x x. x.] is a common West African bell pattern. For example, it is used in the Mpr e rhythm at Ashanti in Ghana [32].
E (7.16) = [x .. xxx. xx x.] is a rhythmic samba necklace from Brazil. Samba rhythm [xx. xxx. x. x.] is obtained by starting E (7.16) on the last beat. When E (7.16) begins on the fifth accented lobe, this is the pattern of the claps from Ghana [24].
E (9.16) = [x. x xxx x xx x.] is a necklace of rhythms from the Central African Republic [2]. When it starts on the fourth beat, it is the rhythm played in West and Central Africa [15], as well as the Kau-bell drawing in a Brazilian samba [29]. When it starts on the penultimate beat, this is a bell drawing from the rhythms of Ngbaka-Maibo in the Central African Republic [2].
E (11.24) = [x .. xxxxx. xxxx x.] is a necklace of aka pygmy rhythms from Central Africa [2]. It usually begins on the seventh lobe.
E (13.24) = [x. x xxxxx x xxxx x.] This is another necklace of aka Pygmy rhythms from Upper Sang [2]. It usually starts on the fourth beat.
In the study of combinatorics of words and sequences, there is a family of strings called Euclidean strings [11]. In this section, we explore the relationship that exists between Euclidean strings and Euclidean rhythms. We will use the terminology and notation introduced in [11].

Figure 3: Two right turns of the Bembé line: a) Bembé b) rotation by one division c) rotation by seven divisions
Let P = (p 0 , p 1 , ..., p n − 1 ) denote a string of positive integers. Let ρ (P) denote the rotation of P one position to the right, that is, ρ (P) = (p n − 1 , p 0 , p 1 , ..., p n − 2 ) , and let ρ d ( P) denotes the rotation of P to the right by d positions. Figure 3 illustrates the operator ρ (P) with P equivalent to the rhythm of the Bembé bell in West Africa [32]. Figure 3 (a) shows the Bembé bell rhythm , Figure 3 (b) shows ρ (P) , this is the rhythm of pops from West Africa [24], and Figure 3 © shows ρ 7 (P) , which is the Tambú rhythm from Curaçao [28 ].
Ellis et al. [11], define the string P = (p 0 , p 1 , ..., p n − 1 ) as a Euclidean string , if increasing p 0 by one and decreasing p n − 1 by one gives a new string, denoted as τ (P) , which is the rotation of P , i.e., P and τ (P) are instances of the same necklace. Thus, if we represent rhythms as binary sequences, Euclidean rhythms cannot be Euclidean strings, because due to the properties of the algorithm used, all Euclidean rhythms begin with one. Increasing p 0 by one will make a two of it, and the string will cease to be a binary sequence. Therefore, in order to investigate the connection between Euclidean strings and Euclidean rhythms, here we will represent rhythms through connecting inter-impact durations of interval vectors (interval vectors for short), which also form strings of non-negative integers. As an example, consider the Turkish rhythm Aksak [6] defined as E (4.9) = [xxxx.]. In the interval-vector notation, we obtain that E (4.9) = (2223). Now τ (2223) = (3222), which is the rotation of E (4,9), and is thus a Euclidean string. In fact, for P = E (4.9), τ (P) = ρ 3 (P) . As a second example, consider the West African rhythm of pops, shown in Figure 3 (b), and set by P = (1221222). We see that τ (P) = (2221221) = ρ 6 (P) , the figure shown in Figure 3 ©, which is also a mirror image of P along the axis (0.6). Thus, P is a Euclidean string. However, note that P is not a Euclidean rhythm. However, P is the rotation of the Euclidean rhythm E (7,12) = (2122122).
Ellis et al. [11] get many excellent results on Euclidean lines. They show that Euclidean lines exist if and only if n and (p 0 , p 1 , ..., p n − 1 ) are mutually prime numbers, and that, when they exist, they are unique. They also show how to create Euclidean lines using an algorithm that has the same structure as the Euclidean algorithm. In addition, they relate Euclidean strings to many other families of sequences studied in the combinatorics of words [1], [19].
Let R (P) denote the string, inverse P (mirror reflection), that is, R (P) = (p n − 1 , p n − 2 , ..., p 1 , p 0 ) . For example, for the Aksak rhythm, where P = (2223), we get R (P) = (3222), i.e., R (P) implies the performance of the P rhythm backwards starting from the same beat. Now we can determine which of the Euclidean rhythms used in the music of the world listed above are Euclidean strings or reverse Euclidean strings. The length of a Euclidean string is determined by the number of numbers included in it. In the rhythm sphere, the number of accented beats that the rhythm contains. In addition, it is obvious that one-character strings are Euclidean strings. Thus, all trivial Euclidean rhythms with one accented beat, such as E (1,2) = [x. ] = (2), E (1,3) = [x. .] = (3), and E (1,4) = [x ....] = (4), and so on, are both Euclidean strings and reverse Euclidean strings. In the following list, Euclidean rhythms are shown in both traditional notation and interval-vector representation. Also lists the styles of music that use these rhythms. Finally, if only the reverse version of the Euclidean rhythm is performed, it is included in the list, but is described as a necklace.
The following Euclidean rhythms are Euclidean strings:
E (2,5) = [xx.] = (23) (classical music, jazz, and Persian music).
E (3.7) = [xxx.] = (223) (Bulgarian folk music).
E (4.9) = [xxxx.] = (2223) (Turkish).
E (5.11) = [xxxxx.] = (22223) (classical music).
E (5.16) = [x .. x .. x .. x .. x ....] = (33334) (brazilian necklace).
The following Euclidean rhythms are inverse Euclidean strings:
E (2,3) = [x. x] = (21) (West Africa, Latin America).
E (3.4) = [x. xx] = (211) (Trinidad, Persia).
E (3,5) = [xx x] = (221) (Romanian and Persian necklaces).
E (3.8) = [x .. x .. x.] = (332) (West Africa).
E (4.7) = [xxx x] = (2221) (Bulgaria).
E (4.11) = [x .. x .. x .. x.] = (3332) (Frank Zappa).
E (5.6) = [x. xxxx] = (21111) (Arabic music).
E (5.7) = [x. x x. xx] = (21211) (Arabic music).
E (5.9) = [xxxx x] = (22221) (Arabic rhythms, South African and Romanian necklaces).
E (5.12) = [x .. xx. x. x.] = (32322) (South Africa).
E (7.8) = [x. xxxxxx] = (2111111) (rhythm of the Tuareg in Libya).
E (7.16) = [x .. xxx. xx x.] = (3223222) (Brazilian necklace).
E (11.24) = [x .. xxxxx. xxxx x.] = (32222322222) (Central Africa).
The following Euclidean rhythms are neither Euclidean nor inverse Euclidean strings:
E (5.8) = [x. x x. xx.] = (21212) (West Africa).
E (7.12) = [x. x xx x x. x.] = (2122122) (West Africa).
E (9.16) = [x. x xxx x xx x.] = (212221222) (West and Central Africa, and Brazilian necklaces).
E (13.24) = [x. x xxxxx x xxxx x.] = (2122222122222) (Central African Necklace).
We have described a new family of musical rhythms, called Euclidean rhythms, which can be obtained using Bjorklund's algorithm for generating sequences, which has the same structure as the Euclidean algorithm. It has been shown that many of the rhythms used in the music of the world are Euclidean rhythms. Some of these Euclidean rhythms are also Euclidean strings [11].
The three groups of Euclidean rhythms presented in the previous section reveal an attractive pattern. Those Euclidean rhythms that are also Euclidean strings (the first four of the first group) are used in classical music, jazz, Bulgarian, Turkish and Persian music, but not popular in African music. Euclidean rhythms that are neither Euclidean strings nor inverted Euclidean strings (the first two of the third group) are used only in the music of Black Africa. Finally, Euclidean rhythms, which are inverse Euclidean strings (the second group), seem to have a much greater appeal. The search for musicological explanations for the obvious preferences of these mathematical properties gives rise to an interesting ethno-musicological problem.
The Euclidean strings described in [11] define another family of rhythms, many of which are also used in the music of the world, but not necessarily Euclidean rhythms, such as (1221222), Afro-Cuban bell rhythm. Thus, it would be interesting to investigate empirically the relationship between Euclidean strings and rhythms in world music, and formally determine the exact mathematical relationship between Euclidean rhythms and Euclidean strings.
From translator
In Sonic Pi, there is a spread function that takes two numeric parameters and returns a set of values for generating a rhythm. In the description of this function there is a link to the work "The Euclidean Algorithm Generates Traditional Musical Rhythms". This brilliant article, published already in 2005, seems to have not been translated into Russian. Not being a translation specialist, I tried, nevertheless, to fill this gap.
A little explanation about the word “necklace”: in the text of the article “necklace”, there is no such term in musical theory, as far as I know. I suppose that this is just some kind of visual intuition of the author, indeed, the rhythmic ring, in the form in which it is presented in the drawings, resembles a necklace - that's why I translate it.
Abstract
The Euclidean algorithm (which reached us from the Euclidean Principles) calculates the greatest common divisor of two integers. This paper demonstrates that the structure of the Euclidean algorithm can be used to very effectively generate a large family of rhythms used as pulsations ( ostinato ), particularly in tropical Africa, and in traditional music in general. These rhythms, called here Euclidean rhythms, have the property that their percussion patterns are distributed as evenly as possible. Euclidean rhythms also find application in accelerators in atomic physics and computer science, and are closely related to several families of words and sequences studied by combinatorics of words, such as Euclidean strings, with which Euclidean rhythms are compared.
1. Introduction
What is common to African rhythms, splitting neutron accelerators (S N S - spallation neutron source) in atomic physics, string theory in computer science and the ancient algorithm described by Euclidean? The short answer is: the patterns are distributed as evenly as possible. To get a longer answer, read on.
')
Mathematics and music are closely related to the times of Pythagoras. However, for the most part their interaction was in the realm of tones and scales. For historical examples of such an interaction, we will refer the reader to the excellent report by Coxeter [9]. On the other hand, the rhythm throughout the story was largely ignored. In this work, we establish certain mathematical connections between the musical rhythm and other areas of knowledge, such as atomic physics and computer science, as well as the work of another famous ancient Greek mathematician, Euclid of Alexandria.
2. Time systems in neutron accelerators
Bjorklund examines the following problem [5], [4] in connection with the operation of some components (such as high-voltage power sources) of fissioning neutron accelerators (SNS) used in atomic physics. The time is divided into intervals (in the case of the SNS accelerator 10 seconds). At some of these intervals, the time system turns on the shutter, generating pulses for this task. For a given number of n time intervals and another number k < n is the number of pulses, the task is to distribute the pulses as uniformly as possible over these intervals. Bjorklund [5] represents this problem in the form of a binary sequence of k ones and n - k zeros, where each number denotes a time interval, and the ones denote pulses. The task then comes down to the following: build a binary sequence of n bits with k ones, so that the units are evenly distributed among the zeros. If k is divisible completely (without remainder) by n , then the solution is obvious. For example, if n = 16 and k = 4, then the solution is [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0]. The task is of interest when k and n are mutually prime numbers [23], that is, when k and n do not have common divisors other than one.
We will describe the Björklund algorithm using one of its examples. Consider a sequence with n = 13 and k = 5. Since 13 is 5 = 8, we begin by considering a sequence of 5 ones followed by 8 zeros, which can also be represented as 13 sequences of one bit:
[1 1 1 1 1 0 0 0 0 0 0 0 0]
We begin to move the zeros, placing zero after each unit, and we get five sequences of two bits, and three more zeros:
[10] [10] [10] [10] [10] [0] [0] [0]
Then we distribute the three remaining zeros in the same way, placing [0] after each sequence [10], and we get:
[100] [100] [100] [10] [10]
Now we have three sequences of three bits, and two sequences of two bits remain. Therefore, we continue in the same way, placing the sequence [10] after each sequence [100], and we get:
[10010] [10010] [100]
The process ends when the remainder contains only one sequence (in our case, the sequence [100]), or we end with zeros. The final sequence is thus the concatenation of [10010], [10010] and [100]:
[1 0 0 1 0 1 0 0 1 0 1 0 0]
Note that you can take another step and insert [100] between [10010] and [10010]. However, Björklund argues that since the sequence is cyclic, it does not matter (hence its stop rule). Bjorklund [5] proved that the final sequence can be built from the original sequence using O (n) arithmetic operations in the worst case.
3. Euclidean algorithm
One of the oldest known algorithms, described in the Euclidean Principles (ca. 300 BC) in Proposition 2 of Book VII , which today is called the Euclidean algorithm, finds the greatest common divisor of two given integers [12], [14]. The idea is very simple. The smaller of the numbers is successively subtracted from the larger until we reach zero, or we get a number that is smaller than the smaller of the two given numbers, in this case it is called the remainder. This residue is then again subtracted sequentially from a smaller number in order to obtain a new residue. This process continues until the residue is zero. For more specificity, consider the example of the numbers 5 and 8, which we used above. First, 8 is divided by 5 with a remainder of 3. Then 5 is divided by 3 with a remainder of 2. Then 3 is divided by 2 with a remainder of 1. Finally, 2 is divided by 2 with a remainder of 0. The greatest common divisor is thus 1. Although the original Euclidean algorithm used this way sequential subtraction, ordinary division will also work, and even faster. The steps of this process can be summarized by the following sequence of equations:
8 = (1) (5) + 3
5 = (1) (3) + 2
3 = (1) (2) + 1
2 = (1) (2) + 0
This algorithm can be briefly described in a recursive manner, as was done in [8]. Let m and k be initial numbers, where m> k .
EUCLID ( m, k )
1. if k = 0
2. then return m
3. else return EUCLID ( k , m mod k )
Running this algorithm with m = 8 and k = 5, we get:
EUCLID (8,5) = EUCLID (5,3) = EUCLID (3,2) = EUCLID (2,1) = EUCLID (1,0) = 1
From the description of the Euclidean algorithm it is clear that if m and k are equal to the number of zeros and ones in the binary sequence respectively (where n = m + k ), then the structure of the Euclidean algorithm is the same as the structure of the Björklund algorithm described above. Indeed, Björklund's algorithm uses division in the form of sequential subtraction, just as Euclid did in the Beginnings [12]. It is also well known that the EUCLID ( m, k ) algorithm being applied to two O (n) -bit numbers (binary sequences of length n ) will require O (n) arithmetic operations in the worst case [8].
4. Euclidean rhythms in traditional ethnic music
The method of presenting musical rhythms in the form of binary sequences is widespread, where each bit is treated as a unit of time (for example, sixteenth note), and the zero bit represents silence (or nonaccented note), while the single bit represents attack (or beginning) of note [31 ]. Therefore, binary sequences generated by the Björklund algorithm as described above can be considered as one family of rhythms. Moreover, since the Björklund algorithm has the same structure as the Euclidean algorithm, we will call these rhythms Euclidean rhythms and denoted E (k, n) , where k means the number of ones, and n is the total length of the sequence (zeroes and ones). For example, E (5, 13) = [1001010010100]. The notation of zeros and ones is not ideal for representing binary rhythms, since it is difficult to visualize the positions of the beats and the length of the interimpact intervals. In music literature, the symbol 'x' is usually used for a single bit and the symbol '.' for zero bit. In this more traditional notation, the previous rhythm is written as E (5, 13) = [x .. xx. xx.].
The rhythm E (5, 13) is a cyclical rhythm with a length (size) of 13 beats. This is not the most common size in world music. Consider for contrast two common values of k and n ; namely, what is E (3, 8)? By applying the Euclidean algorithm to the corresponding sequence [1 1 1 0 0 0 0 0], the reader can easily verify that the result is the Euclidean rhythm E (3, 8) = [x .. x .. x.]. This rhythm illustrates a polygon (triangle) in Figure 1 (a), another convenient and common way of representing cyclical rhythms [31], where it is assumed that the rhythm starts at a point labeled “zero”, time moves clockwise, and the numbers by The sides of the triangle are inter-impact intervals. In fact, this is an even more compact representation of the rhythm in the form of an inter-impact duration of the interval vector [32].
Figure 1: (a) Euclidean rhythm E (3, 8) is a Cuban tresillo , (b) Euclidean rhythm E (5, 8) is a Cuban cinquillo .
The Euclidean rhythm E (3, 8), shown in Figure 1 (a) is one of the most famous on the planet. In Cuba, it is called tresillo , and in the USA it is known as the habanera rhythm, used in hundreds of rockabilly songs throughout the 1950s. He can often be heard in early rock and roll hits in the figures in his left hand on keyboards or performed in a double bass or saxophone part [7], [15], [22]. A good example is the Elvis Presley bass rhythm. The tresillo figure is also widespread in West African folk music. For example, it is played on the atok e bell in Sohu and Ew e dances from Ghana [16]. It is also possible to recognize tresillo in the first cycle of the omnipresent clav e Son , given in the form [x .. x .. x ... xx. .].
In the two previous examples ( E (5, 13) and E (3, 8)) the number of ones is less than the number of zeros. If instead the number of ones is greater than the number of zeros, Bjorklund's algorithm gives the following steps, for example, for k = 5 and n = 8.
[1 1 1 1 1 0 0 0]
[10] [10] [10] [1] [1]
[101] [101] [10]
[1 0 1 1 0 1 1 0]
The resulting Euclidean rhythm E (5, 8) = [x. x x. xx.]. This rhythm illustrates a polygon (pentagon) in Figure 1 (b). This is another famous rhythm on the world stage. In Cuba, it is known as cinquillo and is internally related to tresillo [15]. It was used in jazz throughout the 20th century [27], as was the rockabilly music of the 1950s. For example, this is a picture of the clapping of the palm in Hound Dog by Elvis Presley [7]. The cinquillo figure is also widespread in the traditional music of West Africa [26], [31].
In the remainder of this section, we describe some of the most common Euclidean rhythms in the music of the world. In some cases, Euclidean rhythm is a reversed (rotated, formed by turning - translation ) version of the widely used rhythm. If the rhythm is a reversed version of the other, we say that both belong to the same necklace. Thus, a rhythm necklace is a model of inter-stroke durations that does not take into account the starting point of a cycle. An example of two rhythms that are instances of the same necklace is shown in Figure 2.
Figure 2. These two rhythms are variations of the same rhythmic necklace.
The simplest rhythms have the value k = 1. This subfamily of Euclidean rhythms gives:
E (1, 2) = [x.]
E (1, 3) = [x. .]
E (1, 4) = [x ....], Etc.
Note that since we are interested in cyclical non-periodic rhythms, there is no need to list rhythms that use the factors k and n . For example, multiplying (1, 3) by 4, we get (4, 12), which gives the rhythm:
E (4, 12) = [x .. x .. x .. x ..],
which in turn is periodic with four repetitions E (1, 3) = [x. .]. By the way, E (4, 12) = [x .. x .. x .. x. .] Is the Fandango pattern of 12/8 in flamenco music in northern Spain, where 'x' denotes a loud bang, and '.' quiet cotton [10].
E (2, 3) = [x. x] is a common Afro-Cuban percussion figure. For example, it is found in the conga rhythm in Swing Tumbao (6/8) [18]. It is also common in Latin American music, such as in Cueca [33].
E (2, 5) = [xx.] Is the thirteenth century Persian rhythm, which is called Khafif-e-ramal [34]. This is also a metric drawing of the second part of Tchaikovsky's Symphony No. 6 [17]. When it starts with a second accent ([x .. x.]), It’s the metric figure from Dave Brubeck’s Take Five , as well as from Mars in Gustav Holst’s Planets [17].
E (3, 4) = [x. xx] is the archetypical pulsation of Cumbia from Colombia [20], as well as the rhythm of Calypso from Trinidad [13]. This is also the thirteenth century Persian rhythm called Khalif-e-saghil [34], and the trochoid choreic rhythmic pattern from ancient Greece [21].
E (3, 5) = [xx x], when it starts on the second accentuated beat, is another Persian rhythm of the thirteenth century, called Khafif-e-ramal [34], as well as the rhythm of the Romanian folk dance [25].
E (3, 7) = [xxx.] Is the Ruchenitza rhythm used in the Bulgarian folk dance [24]. This is also a metric drawing in Money Pink Floyd.
E (3, 8) = [x .. x .. x.] Is the Cuban tresillo pattern, which we discussed above [15].
E (4, 7) = [xxx x] is another version of the rhythm of the Bulgarian folk dance Ruchenitza [24].
E (4, 9) = [xxxx.] Is the Turkish rhythm Aksak [6]. This is also the metric drawing used by Dave Brubeck in the play Rondo a la Turk [17].
E (4, 11) = [x .. x .. x .. x.] Is the metric figure used by Frank Zappa in his play entitled Outsid e Now [17].
E (5, 6) = [x. xxxx] gives the York-Samai pattern , a popular Arabic rhythm, when it starts on the second accentuated beat [30].
E (5, 7) = [x. x x. xx] is a Nawakhat drawing, another popular Arabic rhythm [30].
E (5, 8) = [x. x x. xx.] is the Cuban rhythm cinquillo discussed above [15]. When it begins with a second accent, it is also Spanish tango [13] and the thirteenth century Persian rhythm Al-saghilal-sani [34].
E (5.9) = [xxxx x] is the popular Arabic rhythm Agsag-Samai [30]. When it starts at the second accent, it is the drum pattern used by Venda in South Africa [26], as well as the Romanian folk dance rhythm [25].
E (5.11) = [xxxxx.] Is a metric drawing used by Mussorgsky in Pictures at an Exhibition [17].
E (5.12) = [x .. xx. x. x.] is a Venda clap from a South African children's song [24].
E (5.16) = [x .. x .. x .. x .. x ....] Is the rhythmic necklace of the Brazilian boss nova . Usually the boss-new rhythm begins on the third accentuated beat as follows: [x .. x .. x ... x .. x. .] [31]. However, there are other starting points, such as [x .. x .. x .. x ... x. .] [3].
E (7.8) = [x. xxxxxx] is a typical rhythm played on the Bendir (frame drum) and used as an accompaniment to Tuareg songs in Libya [30].
E (7.12) = [x. x xx x x. x.] is a common West African bell pattern. For example, it is used in the Mpr e rhythm at Ashanti in Ghana [32].
E (7.16) = [x .. xxx. xx x.] is a rhythmic samba necklace from Brazil. Samba rhythm [xx. xxx. x. x.] is obtained by starting E (7.16) on the last beat. When E (7.16) begins on the fifth accented lobe, this is the pattern of the claps from Ghana [24].
E (9.16) = [x. x xxx x xx x.] is a necklace of rhythms from the Central African Republic [2]. When it starts on the fourth beat, it is the rhythm played in West and Central Africa [15], as well as the Kau-bell drawing in a Brazilian samba [29]. When it starts on the penultimate beat, this is a bell drawing from the rhythms of Ngbaka-Maibo in the Central African Republic [2].
E (11.24) = [x .. xxxxx. xxxx x.] is a necklace of aka pygmy rhythms from Central Africa [2]. It usually begins on the seventh lobe.
E (13.24) = [x. x xxxxx x xxxx x.] This is another necklace of aka Pygmy rhythms from Upper Sang [2]. It usually starts on the fourth beat.
5. Euclidean lines
In the study of combinatorics of words and sequences, there is a family of strings called Euclidean strings [11]. In this section, we explore the relationship that exists between Euclidean strings and Euclidean rhythms. We will use the terminology and notation introduced in [11].
Figure 3: Two right turns of the Bembé line: a) Bembé b) rotation by one division c) rotation by seven divisions
Let P = (p 0 , p 1 , ..., p n − 1 ) denote a string of positive integers. Let ρ (P) denote the rotation of P one position to the right, that is, ρ (P) = (p n − 1 , p 0 , p 1 , ..., p n − 2 ) , and let ρ d ( P) denotes the rotation of P to the right by d positions. Figure 3 illustrates the operator ρ (P) with P equivalent to the rhythm of the Bembé bell in West Africa [32]. Figure 3 (a) shows the Bembé bell rhythm , Figure 3 (b) shows ρ (P) , this is the rhythm of pops from West Africa [24], and Figure 3 © shows ρ 7 (P) , which is the Tambú rhythm from Curaçao [28 ].
Ellis et al. [11], define the string P = (p 0 , p 1 , ..., p n − 1 ) as a Euclidean string , if increasing p 0 by one and decreasing p n − 1 by one gives a new string, denoted as τ (P) , which is the rotation of P , i.e., P and τ (P) are instances of the same necklace. Thus, if we represent rhythms as binary sequences, Euclidean rhythms cannot be Euclidean strings, because due to the properties of the algorithm used, all Euclidean rhythms begin with one. Increasing p 0 by one will make a two of it, and the string will cease to be a binary sequence. Therefore, in order to investigate the connection between Euclidean strings and Euclidean rhythms, here we will represent rhythms through connecting inter-impact durations of interval vectors (interval vectors for short), which also form strings of non-negative integers. As an example, consider the Turkish rhythm Aksak [6] defined as E (4.9) = [xxxx.]. In the interval-vector notation, we obtain that E (4.9) = (2223). Now τ (2223) = (3222), which is the rotation of E (4,9), and is thus a Euclidean string. In fact, for P = E (4.9), τ (P) = ρ 3 (P) . As a second example, consider the West African rhythm of pops, shown in Figure 3 (b), and set by P = (1221222). We see that τ (P) = (2221221) = ρ 6 (P) , the figure shown in Figure 3 ©, which is also a mirror image of P along the axis (0.6). Thus, P is a Euclidean string. However, note that P is not a Euclidean rhythm. However, P is the rotation of the Euclidean rhythm E (7,12) = (2122122).
Ellis et al. [11] get many excellent results on Euclidean lines. They show that Euclidean lines exist if and only if n and (p 0 , p 1 , ..., p n − 1 ) are mutually prime numbers, and that, when they exist, they are unique. They also show how to create Euclidean lines using an algorithm that has the same structure as the Euclidean algorithm. In addition, they relate Euclidean strings to many other families of sequences studied in the combinatorics of words [1], [19].
Let R (P) denote the string, inverse P (mirror reflection), that is, R (P) = (p n − 1 , p n − 2 , ..., p 1 , p 0 ) . For example, for the Aksak rhythm, where P = (2223), we get R (P) = (3222), i.e., R (P) implies the performance of the P rhythm backwards starting from the same beat. Now we can determine which of the Euclidean rhythms used in the music of the world listed above are Euclidean strings or reverse Euclidean strings. The length of a Euclidean string is determined by the number of numbers included in it. In the rhythm sphere, the number of accented beats that the rhythm contains. In addition, it is obvious that one-character strings are Euclidean strings. Thus, all trivial Euclidean rhythms with one accented beat, such as E (1,2) = [x. ] = (2), E (1,3) = [x. .] = (3), and E (1,4) = [x ....] = (4), and so on, are both Euclidean strings and reverse Euclidean strings. In the following list, Euclidean rhythms are shown in both traditional notation and interval-vector representation. Also lists the styles of music that use these rhythms. Finally, if only the reverse version of the Euclidean rhythm is performed, it is included in the list, but is described as a necklace.
The following Euclidean rhythms are Euclidean strings:
E (2,5) = [xx.] = (23) (classical music, jazz, and Persian music).
E (3.7) = [xxx.] = (223) (Bulgarian folk music).
E (4.9) = [xxxx.] = (2223) (Turkish).
E (5.11) = [xxxxx.] = (22223) (classical music).
E (5.16) = [x .. x .. x .. x .. x ....] = (33334) (brazilian necklace).
The following Euclidean rhythms are inverse Euclidean strings:
E (2,3) = [x. x] = (21) (West Africa, Latin America).
E (3.4) = [x. xx] = (211) (Trinidad, Persia).
E (3,5) = [xx x] = (221) (Romanian and Persian necklaces).
E (3.8) = [x .. x .. x.] = (332) (West Africa).
E (4.7) = [xxx x] = (2221) (Bulgaria).
E (4.11) = [x .. x .. x .. x.] = (3332) (Frank Zappa).
E (5.6) = [x. xxxx] = (21111) (Arabic music).
E (5.7) = [x. x x. xx] = (21211) (Arabic music).
E (5.9) = [xxxx x] = (22221) (Arabic rhythms, South African and Romanian necklaces).
E (5.12) = [x .. xx. x. x.] = (32322) (South Africa).
E (7.8) = [x. xxxxxx] = (2111111) (rhythm of the Tuareg in Libya).
E (7.16) = [x .. xxx. xx x.] = (3223222) (Brazilian necklace).
E (11.24) = [x .. xxxxx. xxxx x.] = (32222322222) (Central Africa).
The following Euclidean rhythms are neither Euclidean nor inverse Euclidean strings:
E (5.8) = [x. x x. xx.] = (21212) (West Africa).
E (7.12) = [x. x xx x x. x.] = (2122122) (West Africa).
E (9.16) = [x. x xxx x xx x.] = (212221222) (West and Central Africa, and Brazilian necklaces).
E (13.24) = [x. x xxxxx x xxxx x.] = (2122222122222) (Central African Necklace).
6. Concluding remarks
We have described a new family of musical rhythms, called Euclidean rhythms, which can be obtained using Bjorklund's algorithm for generating sequences, which has the same structure as the Euclidean algorithm. It has been shown that many of the rhythms used in the music of the world are Euclidean rhythms. Some of these Euclidean rhythms are also Euclidean strings [11].
The three groups of Euclidean rhythms presented in the previous section reveal an attractive pattern. Those Euclidean rhythms that are also Euclidean strings (the first four of the first group) are used in classical music, jazz, Bulgarian, Turkish and Persian music, but not popular in African music. Euclidean rhythms that are neither Euclidean strings nor inverted Euclidean strings (the first two of the third group) are used only in the music of Black Africa. Finally, Euclidean rhythms, which are inverse Euclidean strings (the second group), seem to have a much greater appeal. The search for musicological explanations for the obvious preferences of these mathematical properties gives rise to an interesting ethno-musicological problem.
The Euclidean strings described in [11] define another family of rhythms, many of which are also used in the music of the world, but not necessarily Euclidean rhythms, such as (1221222), Afro-Cuban bell rhythm. Thus, it would be interesting to investigate empirically the relationship between Euclidean strings and rhythms in world music, and formally determine the exact mathematical relationship between Euclidean rhythms and Euclidean strings.
Bibliography
[1] J.-P. Allouche and JO Shallit. Automatic Sequences. Cambridge University Press, Cambridge, England, 2002.
[2] Simha Arom. African Polyphony and Polyrhythm. Cambridge University Press, Cambridge, England, 1991.
[3] Gerard Behague. Bossa and bossas: recent changes in Brazilian urban popular music. Ethnomusicology, 17 (2): 209–233, 1973.
[4] E. Bjorklund. A metric for measuring the evenness of the timing system rep-rate patterns. SNS ASD Technical Note SNS-NOTE-CNTRL-100, Los Alamos National Laboratory, Los Alamos, USA, 2003.
[5] E. Bjorklund. The theory of rep-rate pattern generation in the SNS timing system. SNS ASD Technical Note SNS-NOTE-CNTRL-99, Los Alamos National Laboratory, Los Alamos, USA, 2003.
[6] C. Brauloiu. Le rythme aksak. Revue de Musicologie, 23: 71–108, 1952.
[7] Roy Brewer. The use of Habanera rhythm in rockabilly music. American Music, 17: 300–317, Autumn 1999.
[8] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms. The MIT Press, Cambridge, Massachussetts, 2001.
[9] HSM Coxeter. Music and mathematics. The Canadian Music Journal, VI: 13–24, 1962.
[10] Miguel Díaz-Bañez, Giovanna Farigu, Francisco Gómez, David Rappaport, and Godfried T. Toussaint. El compás flamenco: a phylogenetic analysis. Instruction from BRIDGES: Mathematical Connections in Art, Music and Science, Southwestern College, Winfield, Kansas, July 30 - August 1 2004.
[11] John Ellis, Frank Ruskey, Joe Sawada, and Jamie Simpson. Euclidean strings. Theoretical Computer Science, 301: 321–340, 2003.
[12] Euclid. Elements. Dover, 1956. Translated by Sir Thomas L. Heath.
[13] Bob Evans. Authentic Conga Rhythms. Belwin Mills Publishing Corporation, Miami, 1966.
[14] Philip Franklin. The Euclidean algorithm. The American Mathematical Monthly, 63 (9): 663–664, November 1956.
[15] SA Floyd Jr. Black music in the circum-Caribbean. American Music, 17 (1): 1–38, 1999.
[16] R. Kauffman. African rhythm: A reassessment. Ethnomusicology, 24 (3): 393–415, Sept. 1980
[17] Michael Keith. From Polychords to Pólya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991.
[18] Töm Klöwer. The Joy of Drumming: Drums and Percussion Instruments from Around the World. Binkey Kok Publications, Diever, Holland, 1997.
[19] M. Lothaire. Algebraic Combinatorics on Words. Cambridge University Press, Cambridge, England, 2002.
[20] Peter Manuel. The anticipated bass in Cuban popular music. Latin American Music Review, 6 (2): 249–261, Autumn-Winter 1985.
[21] Thomas J. Mathiesen. Rhythm and meter in ancient Greek music. Music Theory Spectrum, 7: 159–180, Spring 1985.
[22] Craig Morrison. Go Cat Go: Rockabilly Music and Its Makers. University of Illinois Press, Urbana, 1996.
[23] C. Stanley Ogilvy and John T. Anderson. Excursions in Number Theory. Oxford University Press, New York, 1966.
[24] Jeff Pressing. Cognitive isomorphisms between West Africa, the Balkans and Western tonality. Studies in Music, 17: 38–61, 1983.
[25] Vera Proca-Ciortea. On rhythm in Rumanian folk dance. Yearbook of the International Folk Music Council, 1: 176–199, 1969.
[26] Jay Rahn. Asymmetrical ostinatos in sub-saharan music: time, pitch, and cycles reconsidered. In Theory Only, 9 (7): 23–37, 1987.
[27] Jay Rahn. Turning the analysis around: African-derived rhythms and European-derived music theory. Black Music Research Journal, 16(1):71–89, 1996.
[28] Rene V. Rosalia. Migrated Rhythm: The Tambú of Curaçao. CaribSeek, 2002.
[29] Doug Sole. The Soul of Hand Drumming. Mel Bay Productions Inc., Toronto, 1996.
[30] James A. Standifer. The Tuareg: their music and dances. The Black Perspective in Music, 16(1):45–62, Spring 1988.
[31] Godfried T. Toussaint. A mathematical analysis of African, Brazilian, and Cuban clave rhythms. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 157–168, Towson University, Towson, MD, July 27-29 2002.
[32] Godfried T. Toussaint. Classification and phylogenetic analysis of African ternary rhythm timelines. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 25–36, Granada, Spain, July 23-27 2003.
[33] Pedro van der Lee. Zarabanda: esquemas rítmicos de acompañamiento en 6/8. Latin American Music Review, 16(2):199–220, Autumn-Winter 1995.
[34] O. Wright. The Modal System of Arab and Persian Music AD 1250-1300. Oxford University Press, Oxford, England, 1978.
Literature
[1] J.-P. Allouche and JO Shallit. Automatic Sequences. Cambridge University Press, Cambridge, England, 2002.
[2] Simha Arom. African Polyphony and Polyrhythm. Cambridge University Press, Cambridge, England, 1991.
[3] Gerard Behague. Bossa and bossas: recent changes in Brazilian urban popular music. Ethnomusicology, 17 (2): 209–233, 1973.
[4] E. Bjorklund. A metric for measuring the evenness of the timing system rep-rate patterns. SNS ASD Technical Note SNS-NOTE-CNTRL-100, Los Alamos National Laboratory, Los Alamos, USA, 2003.
[5] E. Bjorklund. The theory of rep-rate pattern generation in the SNS timing system. SNS ASD Technical Note SNS-NOTE-CNTRL-99, Los Alamos National Laboratory, Los Alamos, USA, 2003.
[6] C. Brauloiu. Le rythme aksak. Revue de Musicologie, 23: 71–108, 1952.
[7] Roy Brewer. The use of Habanera rhythm in rockabilly music. American Music, 17: 300–317, Autumn 1999.
[8] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms. The MIT Press, Cambridge, Massachussetts, 2001.
[9] HSM Coxeter. Music and mathematics. The Canadian Music Journal, VI: 13–24, 1962.
[10] Miguel Díaz-Bañez, Giovanna Farigu, Francisco Gómez, David Rappaport, and Godfried T. Toussaint. El compás flamenco: a phylogenetic analysis. Instruction from BRIDGES: Mathematical Connections in Art, Music and Science, Southwestern College, Winfield, Kansas, July 30 - August 1 2004.
[11] John Ellis, Frank Ruskey, Joe Sawada, and Jamie Simpson. Euclidean strings. Theoretical Computer Science, 301: 321–340, 2003.
[12] Euclid. Elements. Dover, 1956. Translated by Sir Thomas L. Heath.
[13] Bob Evans. Authentic Conga Rhythms. Belwin Mills Publishing Corporation, Miami, 1966.
[14] Philip Franklin. The Euclidean algorithm. The American Mathematical Monthly, 63 (9): 663–664, November 1956.
[15] SA Floyd Jr. Black music in the circum-Caribbean. American Music, 17 (1): 1–38, 1999.
[16] R. Kauffman. African rhythm: A reassessment. Ethnomusicology, 24 (3): 393–415, Sept. 1980
[17] Michael Keith. From Polychords to Pólya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991.
[18] Töm Klöwer. The Joy of Drumming: Drums and Percussion Instruments from Around the World. Binkey Kok Publications, Diever, Holland, 1997.
[19] M. Lothaire. Algebraic Combinatorics on Words. Cambridge University Press, Cambridge, England, 2002.
[20] Peter Manuel. The anticipated bass in Cuban popular music. Latin American Music Review, 6 (2): 249–261, Autumn-Winter 1985.
[21] Thomas J. Mathiesen. Rhythm and meter in ancient Greek music. Music Theory Spectrum, 7: 159–180, Spring 1985.
[22] Craig Morrison. Go Cat Go: Rockabilly Music and Its Makers. University of Illinois Press, Urbana, 1996.
[23] C. Stanley Ogilvy and John T. Anderson. Excursions in Number Theory. Oxford University Press, New York, 1966.
[24] Jeff Pressing. Cognitive isomorphisms between West Africa, the Balkans and Western tonality. Studies in Music, 17: 38–61, 1983.
[25] Vera Proca-Ciortea. On rhythm in Rumanian folk dance. Yearbook of the International Folk Music Council, 1: 176–199, 1969.
[26] Jay Rahn. Asymmetrical ostinatos in sub-saharan music: time, pitch, and cycles reconsidered. In Theory Only, 9 (7): 23–37, 1987.
[27] Jay Rahn. Turning the analysis around: African-derived rhythms and European-derived music theory. Black Music Research Journal, 16(1):71–89, 1996.
[28] Rene V. Rosalia. Migrated Rhythm: The Tambú of Curaçao. CaribSeek, 2002.
[29] Doug Sole. The Soul of Hand Drumming. Mel Bay Productions Inc., Toronto, 1996.
[30] James A. Standifer. The Tuareg: their music and dances. The Black Perspective in Music, 16(1):45–62, Spring 1988.
[31] Godfried T. Toussaint. A mathematical analysis of African, Brazilian, and Cuban clave rhythms. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 157–168, Towson University, Towson, MD, July 27-29 2002.
[32] Godfried T. Toussaint. Classification and phylogenetic analysis of African ternary rhythm timelines. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 25–36, Granada, Spain, July 23-27 2003.
[33] Pedro van der Lee. Zarabanda: esquemas rítmicos de acompañamiento en 6/8. Latin American Music Review, 16(2):199–220, Autumn-Winter 1995.
[34] O. Wright. The Modal System of Arab and Persian Music AD 1250-1300. Oxford University Press, Oxford, England, 1978.
Godfrey Toussaint
School of Computer Science, McGill University, Montréal, Québec, Canada
godfried@cs.mcgill.ca The
study was supported by NSERC and FCAR
Source: https://habr.com/ru/post/278265/
All Articles