Simple checksum calculation
When data is transmitted over communication lines, a checksum is used , calculated according to some algorithm. The algorithm is often complex, of course, it is mathematically justified, but it is very inconvenient when there is a shortage of resources, for example, when programming microcontrollers.

To simplify the algorithm, without losing quality, you need a bit of “bit magic,” which is an interesting topic in itself.
Without a checksum, it is dangerous to transmit data, since interference is present everywhere and always, the whole question is only in their probability of occurrence and the side effects caused by them. Depending on the conditions, the algorithm of error detection and the amount of data in the checksum are chosen. The algorithm is more complicated, and the checksum is larger, less errors are not recognized.
')
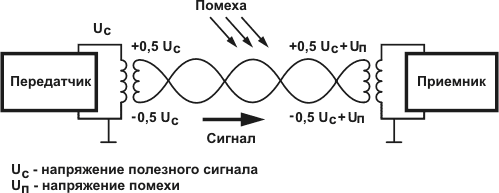
The cause of interference at the physical level, during data transmission.
Here is an example of the most typical algorithm for a microcontroller, which has actually become an industry standard since 1979.
Such code is not weak, there is an option without a table , but slower (bit-by-bit data processing is necessary), in any case able to take out the brain to both the programmer and the microcontroller. Not in any microcontroller the algorithm with the table will get at all.
Let's analyze the algorithms that generally can confirm the integrity of the data with a low price.
In the first place is a simple parity bit. If necessary, the hardware is formed, the principle is the simplest, and is described in detail in Wikipedia . There is only one drawback, it skips double errors (and even an even number of errors), when the parity of all bits does not change. It can be used to collect statistics on the presence of errors in the stream of transmitted data, but data integrity does not guarantee, although it reduces the likelihood of a missed error by 50% (depends, of course, on the type of interference on the line, in this case it is assumed that the number of even and odd failures is equal to ).
To enable the parity bit, often no code is needed, just indicate that the UART should use the parity bit. Typically, simply specify:
Often, developers even forget that the UART has the ability to check bit parity on board. In addition to the integrity of the transmitted data, this allows you to avoid a steady breakdown of synchronization (for example, when transmitting data over the air), when the payload can randomly simulate start and stop bits, and instead of data at the output of the buffer, start and stop bits in random order.
If the parity is small (and this is usually small), an additional checksum is added. Calculate the checksum, you can as the amount of previously transferred bytes, simply and logically
%20%2B%20byte(2)%20%2B%20byte(3)%2B%20...%20%2B%20byte(N))
Naturally, the overflow bits are not taken into account, the result is placed in the 8 bits allocated for the checksum. You can skip the error if, in the event of an accidental failure, one byte is increased by some value, and the other byte is reduced by the same value. Checksum does not change. Let's conduct an experiment on data transfer. Baseline data are as follows:
We transmit a virtual telegram N times. The ideal checksum will reveal an error in the amount of information available to it about the message, more information, a higher probability of detecting a faulty telegram. Probability of missing an error for 1 bit of checksum:
%3D0.5) .
.
For 8 bits:
%3D1%3A256) ,
,
for 256 sent telegrams with an error, one will pass the checksum check. We look at the statistics from virtual data transfer using a simple test program:
Or conditional efficiency = 55% of the capabilities of the “ideal” checksum. Such is the fee for the simplicity of the algorithm and the speed of data processing. In general, for many applications, the algorithm is operational. One addition operation and one 8-bit variable are used. There is no possibility of incorrect implementation. Therefore, the algorithm is used in the ADAMS, ICP controllers as part of the DCON protocol (the parity bit can be included there, the ASCI characters only, which also contributes to improving the reliability of data transmission and the resulting reliability is somewhat higher, as part of the errors are detected by other, additional features not related to checksum).
Despite the probability of passing an error of 1: 143, the probability of finding an error better than 1: 256 is impossible theoretically. There are losses in the quality of work, but this is not always significant. If you need higher reliability, you need to use a checksum with a large number of bits. Or, in other words, a simple checksum does not efficiently use about 0.75 bits out of 8 available bits of information in the checksum.
For comparison, instead of the sum, bitwise XOR is added. It became significantly worse, the probability of detecting an error was 1:67 or 26% of the theoretical limit. Simplified, this can be explained by the fact that XOR changes even fewer bits in the checksum when an error occurs, lower the response to a single bit failure, and a repeated error is more likely to return the checksum to its original state.
It can also be argued that the checksum for XOR is 8 independent checksums of 1 bit. The probability that an error will occur in one of 8 bits is 1: 8, the probability of double failure 1:64, which we observe, the theoretical value coincided with experimental data.
We need such an algorithm to replace with the single error the maximum number of bits in the checksum. But we are, in total, limited by the complexity of the algorithm, and the resources at our disposal. Not all microcontrollers have a hardware CRC calculation unit. But, almost everywhere, there is a multiplication unit. Calculate the checksum as the product of a sequence of bytes, on some "magic" constant:
The constant should be simple, and be large enough to change a larger number of bits after each operation, 211 is quite suitable, we check:
Only 72% of the theoretical limit, a slight improvement over the simple amount. The algorithm in this form does not make sense. In this case, important information from the discarded high bits of 8..16 is lost, and they must be taken into account. The easiest way is to mix the XOR function with the lower bits 1..8. We come to an even more intensive modification of the checksum, preferably with minimal resources. Add focus from cryptographic algorithms
Checking:
The result is 91% of the theoretical limit. It is quite suitable for use.
If there is no multiplication unit in the microcontroller, you can simulate the multiplication of the operations of addition, offset and XOR. The essence of the process is the same, modified by an error bit, evenly “distributed” over the remaining bits of the checksum.
Result:
Surprisingly good result. The average value is 254.5 or 99% of the theoretical limit, operations are slightly more, but they are all simple and no multiplication is used.
If for internal storage of intermediate checksum values we give 16 bits to the variable (but only the lower 8 bits are transmitted via the communication line), which is not a problem even for the weakest microcontroller, we will get some improvement in the operation of the algorithm. In general, saving 8 bits does not make much sense, and the 8-bit intermediate variable was previously used simply to simplify the understanding of the algorithm.
That corresponds to 100.6% of the theoretical limit, quite a good result for such a simple one-line algorithm:
Full 16-bit multiplication is used. Again, it was not without the magic number 44111 (selected from general considerations without going through the entire subset of numbers). More precisely, it makes sense to select a constant only after having decided on the expected type of errors in the data transmission line.
Such a high result is explained by the fact that 2 cycles of multiplication in a row completely mix the bits, which is what we needed. The exception, it seems, is the last byte of the telegram, especially its high bits, they are not fully mixed in the checksum, but the probability that an error will occur in them is small, approximately 4%. This feature practically does not manifest itself statistically, at least on my set of test data and an error limited to 10 failed bits. To exclude this feature, you can do N + 1 iterations by adding a virtual byte in addition to the ones in the test data block (but this is a complication of the algorithm).
Option without multiplication with the same result. The CRC variable is 16-bit, 8-bit data, the result of the algorithm is the lower 8 bits of the checksum found:
The result is 100.6% of the theoretical limit.
The non-multiplication option is simpler, leaving the bare minimum of functions, only 3 mathematical operations:
The result is 86% of the theoretical limit.
In this case, the loss of the most significant bits is not; they are returned to the lower part of the variable through the XOR function (bit mixer).
A slight improvement in some cases gives the same:
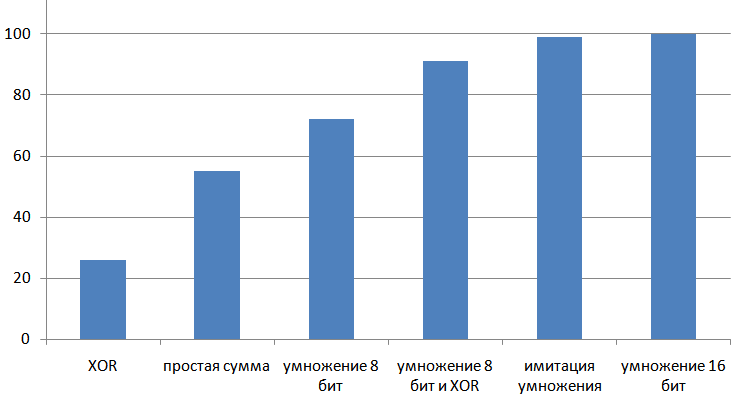
The result of the work of the considered algorithms, from simple and weak, to complex and qualitative:
Further, suppose that 8 bits are not enough for us to form a checksum.

The next option is 16 bits, and the theoretical error probability of the transmitted data is 1: 65536, which is much better. Reliability grows exponentially. But, as a side effect, the amount of auxiliary data is growing, by the example of our telegram, 2 bytes of checksum are added to 8 bytes of useful information.
Simple sum and XOR algorithms, as applied to the 16-bit and subsequent CRCs, are not considered at all, they practically do not improve the quality of work, compared to the 8-bit variants.
We modify the algorithm for processing a checksum of 16 bits, it should be noted that there is also a magic number 8 and 44111, a significant and unreasonable change worsens the work of the algorithm several times.
Result:
That corresponds to 109% of the theoretical limit. There is a measurement error, but it is excusable for 10 million iterations. It also affects the creation algorithm, and in general the type of errors. For a more accurate analysis, in any case, you need to adjust the conditions for errors in a particular data line.
Additionally, I note that you can use 32-bit intermediate variables to accumulate the result, and use the final checksum as the lower 16 bits. In many cases, for any digit of the checksum, the quality of the algorithm improves somewhat.
Let's move on to the 32-bit checksum option. There is a problem with the time devoted to the analysis of statistical data, since the number of transmitted telegrams is already comparable to 2 ^ 32. The algorithm is the same; magic numbers change upwards
Over 10 million iterations, no error was detected. To speed up the collection of statistics cut the CRC to 24 bits:
The result, out of 10 million iterations, the error was detected 3 times
Quite a good result and generally close to the theoretical limit for 24-bit checksum (1: 16777216). Here it should be noted that the data integrity control function is evenly distributed across all CRC bits, and it is quite possible to discard them from any side if there is a limit on the size of the transmitted CRC.
For full-fledged 32 bits, it’s enough to wait long for the result, there are simply no errors, for an acceptable waiting time.
Option without multiplication:
There was no failure for a full-fledged checksum. The checksum trimmed to 24 bits shows approximately the same results, 8 errors per 100 million iterations. Intermediate variable CRC 64-bit.
And finally, 64-bit checksum, the maximum checksum, which makes sense when transferring data at the lower level:
Wait for the data transmission error, until the end of the universe, probably will not work :)

A method similar to that used for the CRC32 showed similar results. More bits are left, higher reliability is in full compliance with the theoretical limit. Checked on the lower 20 and 24 bits, this seems to be quite sufficient to assess the quality of the algorithm.
You can also apply for 128-bit numbers (and even larger ones), the main thing is to choose correctly 128-bit magic constants. But this is clearly not for microcontrollers, such numbers are not supported by the compiler.
In general, the multiplication method is similar to the generation of a pseudo-random sequence, only taking into account the useful data involved in the process.
I recommend to use in microcontrollers, or to check the integrity of any transmitted data. It is a working method, already as it is, despite the simplicity of the algorithm.
My CRC research project on githab .
Further, it would be interesting to optimize the algorithm for more real data (not pseudo-random numbers by the standard algorithm), to select more suitable magic numbers for a number of tasks and initial conditions, I think you can still win fractions of a percent in the quality of the algorithm. Optimize the algorithm for speed, readability of the code (the simplicity of the algorithm), quality of work. Ideally, get and test code samples for all types of microcontrollers, for this you need examples using the multiplication of 8, 16, 32 bit data, and no multiplication at all.

To simplify the algorithm, without losing quality, you need a bit of “bit magic,” which is an interesting topic in itself.
Without a checksum, it is dangerous to transmit data, since interference is present everywhere and always, the whole question is only in their probability of occurrence and the side effects caused by them. Depending on the conditions, the algorithm of error detection and the amount of data in the checksum are chosen. The algorithm is more complicated, and the checksum is larger, less errors are not recognized.
')

The cause of interference at the physical level, during data transmission.

Here is an example of the most typical algorithm for a microcontroller, which has actually become an industry standard since 1979.
Checksum calculation for Modbus protocol
void crc_calculating(unsigned char puchMsg, unsigned short usDataLen) /*## ##*/ { { unsigned char uchCRCHi = 0xFF ; /* CRC */ unsigned char uchCRCLo = 0xFF ; /* CRC */ unsigned uIndex ; /* will index into CRC lookup table */ while (usDataLen--) /* pass through message buffer */ { uIndex = uchCRCHi ^ *puchMsg++ ; /* CRC */ uchCRCLo = uchCRCLo ^ auchCRCHi[uIndex] ; uchCRCHi = auchCRCLo[uIndex] ; } return (uchCRCHi << 8 | uchCRCLo) ; /* Table of CRC values for high–order byte */ static unsigned char auchCRCHi[] = { 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40 }; /* Table of CRC values for low–order byte */ static char auchCRCLo[] = { 0x00, 0xC0, 0xC1, 0x01, 0xC3, 0x03, 0x02, 0xC2, 0xC6, 0x06, 0x07, 0xC7, 0x05, 0xC5, 0xC4, 0x04, 0xCC, 0x0C, 0x0D, 0xCD, 0x0F, 0xCF, 0xCE, 0x0E, 0x0A, 0xCA, 0xCB, 0x0B, 0xC9, 0x09, 0x08, 0xC8, 0xD8, 0x18, 0x19, 0xD9, 0x1B, 0xDB, 0xDA, 0x1A, 0x1E, 0xDE, 0xDF, 0x1F, 0xDD, 0x1D, 0x1C, 0xDC, 0x14, 0xD4, 0xD5, 0x15, 0xD7, 0x17, 0x16, 0xD6, 0xD2, 0x12, 0x13, 0xD3, 0x11, 0xD1, 0xD0, 0x10, 0xF0, 0x30, 0x31, 0xF1, 0x33, 0xF3, 0xF2, 0x32, 0x36, 0xF6, 0xF7, 0x37, 0xF5, 0x35, 0x34, 0xF4, 0x3C, 0xFC, 0xFD, 0x3D, 0xFF, 0x3F, 0x3E, 0xFE, 0xFA, 0x3A, 0x3B, 0xFB, 0x39, 0xF9, 0xF8, 0x38, 0x28, 0xE8, 0xE9, 0x29, 0xEB, 0x2B, 0x2A, 0xEA, 0xEE, 0x2E, 0x2F, 0xEF, 0x2D, 0xED, 0xEC, 0x2C, 0xE4, 0x24, 0x25, 0xE5, 0x27, 0xE7, 0xE6, 0x26, 0x22, 0xE2, 0xE3, 0x23, 0xE1, 0x21, 0x20, 0xE0, 0xA0, 0x60, 0x61, 0xA1, 0x63, 0xA3, 0xA2, 0x62, 0x66, 0xA6, 0xA7, 0x67, 0xA5, 0x65, 0x64, 0xA4, 0x6C, 0xAC, 0xAD, 0x6D, 0xAF, 0x6F, 0x6E, 0xAE, 0xAA, 0x6A, 0x6B, 0xAB, 0x69, 0xA9, 0xA8, 0x68, 0x78, 0xB8, 0xB9, 0x79, 0xBB, 0x7B, 0x7A, 0xBA, 0xBE, 0x7E, 0x7F, 0xBF, 0x7D, 0xBD, 0xBC, 0x7C, 0xB4, 0x74, 0x75, 0xB5, 0x77, 0xB7, 0xB6, 0x76, 0x72, 0xB2, 0xB3, 0x73, 0xB1, 0x71, 0x70, 0xB0, 0x50, 0x90, 0x91, 0x51, 0x93, 0x53, 0x52, 0x92, 0x96, 0x56, 0x57, 0x97, 0x55, 0x95, 0x94, 0x54, 0x9C, 0x5C, 0x5D, 0x9D, 0x5F, 0x9F, 0x9E, 0x5E, 0x5A, 0x9A, 0x9B, 0x5B, 0x99, 0x59, 0x58, 0x98, 0x88, 0x48, 0x49, 0x89, 0x4B, 0x8B, 0x8A, 0x4A, 0x4E, 0x8E, 0x8F, 0x4F, 0x8D, 0x4D, 0x4C, 0x8C, 0x44, 0x84, 0x85, 0x45, 0x87, 0x47, 0x46, 0x86, 0x82, 0x42, 0x43, 0x83, 0x41, 0x81, 0x80, 0x40 }; } } Such code is not weak, there is an option without a table , but slower (bit-by-bit data processing is necessary), in any case able to take out the brain to both the programmer and the microcontroller. Not in any microcontroller the algorithm with the table will get at all.
Let's analyze the algorithms that generally can confirm the integrity of the data with a low price.
Parity bit (1-bit checksum)
In the first place is a simple parity bit. If necessary, the hardware is formed, the principle is the simplest, and is described in detail in Wikipedia . There is only one drawback, it skips double errors (and even an even number of errors), when the parity of all bits does not change. It can be used to collect statistics on the presence of errors in the stream of transmitted data, but data integrity does not guarantee, although it reduces the likelihood of a missed error by 50% (depends, of course, on the type of interference on the line, in this case it is assumed that the number of even and odd failures is equal to ).
To enable the parity bit, often no code is needed, just indicate that the UART should use the parity bit. Typically, simply specify:
enable parity bit on microcontroller
void setup(){ Serial.begin(9600,SERIAL_8N1); // , ; Serial1.begin(38400,SERIAL_8E1); // Serial.println("Hello Computer"); Serial1.println("Hello Serial 1"); } Often, developers even forget that the UART has the ability to check bit parity on board. In addition to the integrity of the transmitted data, this allows you to avoid a steady breakdown of synchronization (for example, when transmitting data over the air), when the payload can randomly simulate start and stop bits, and instead of data at the output of the buffer, start and stop bits in random order.
8-bit checksum
If the parity is small (and this is usually small), an additional checksum is added. Calculate the checksum, you can as the amount of previously transferred bytes, simply and logically
Naturally, the overflow bits are not taken into account, the result is placed in the 8 bits allocated for the checksum. You can skip the error if, in the event of an accidental failure, one byte is increased by some value, and the other byte is reduced by the same value. Checksum does not change. Let's conduct an experiment on data transfer. Baseline data are as follows:
- The data block is 8 bytes.
- Random ($ FF + 1) pseudo-random data population
- Randomly change 1 bit in a data block with an XOR operation with a specially prepared byte, which has one single bit at a random position.
- We repeat the previous paragraph 10 times, this can result in 0 to 10 bad bits (2 errors can be superimposed on each other when restoring data), we ignore the option with 0 bad bits in the future as useless for us.
We transmit a virtual telegram N times. The ideal checksum will reveal an error in the amount of information available to it about the message, more information, a higher probability of detecting a faulty telegram. Probability of missing an error for 1 bit of checksum:
For 8 bits:
for 256 sent telegrams with an error, one will pass the checksum check. We look at the statistics from virtual data transfer using a simple test program:
Statistics
1: 144 (here and below - the probability of passing an error)
1: 143
1: 144
1: 145
1: 144
1: 142
1: 143
1: 143
1: 142
1: 140
Total number of errors 69892 from 10 million iterations, or 1: 143.078
1: 143
1: 144
1: 145
1: 144
1: 142
1: 143
1: 143
1: 142
1: 140
Total number of errors 69892 from 10 million iterations, or 1: 143.078
Or conditional efficiency = 55% of the capabilities of the “ideal” checksum. Such is the fee for the simplicity of the algorithm and the speed of data processing. In general, for many applications, the algorithm is operational. One addition operation and one 8-bit variable are used. There is no possibility of incorrect implementation. Therefore, the algorithm is used in the ADAMS, ICP controllers as part of the DCON protocol (the parity bit can be included there, the ASCI characters only, which also contributes to improving the reliability of data transmission and the resulting reliability is somewhat higher, as part of the errors are detected by other, additional features not related to checksum).
Despite the probability of passing an error of 1: 143, the probability of finding an error better than 1: 256 is impossible theoretically. There are losses in the quality of work, but this is not always significant. If you need higher reliability, you need to use a checksum with a large number of bits. Or, in other words, a simple checksum does not efficiently use about 0.75 bits out of 8 available bits of information in the checksum.
For comparison, instead of the sum, bitwise XOR is added. It became significantly worse, the probability of detecting an error was 1:67 or 26% of the theoretical limit. Simplified, this can be explained by the fact that XOR changes even fewer bits in the checksum when an error occurs, lower the response to a single bit failure, and a repeated error is more likely to return the checksum to its original state.
It can also be argued that the checksum for XOR is 8 independent checksums of 1 bit. The probability that an error will occur in one of 8 bits is 1: 8, the probability of double failure 1:64, which we observe, the theoretical value coincided with experimental data.
We need such an algorithm to replace with the single error the maximum number of bits in the checksum. But we are, in total, limited by the complexity of the algorithm, and the resources at our disposal. Not all microcontrollers have a hardware CRC calculation unit. But, almost everywhere, there is a multiplication unit. Calculate the checksum as the product of a sequence of bytes, on some "magic" constant:
CRC=CRC + byte*211 The constant should be simple, and be large enough to change a larger number of bits after each operation, 211 is quite suitable, we check:
Statistics
1: 185
1: 186
1: 185
1: 185
1: 193
1: 188
1: 187
1: 194
1: 190
1: 200
1: 186
1: 185
1: 185
1: 193
1: 188
1: 187
1: 194
1: 190
1: 200
Only 72% of the theoretical limit, a slight improvement over the simple amount. The algorithm in this form does not make sense. In this case, important information from the discarded high bits of 8..16 is lost, and they must be taken into account. The easiest way is to mix the XOR function with the lower bits 1..8. We come to an even more intensive modification of the checksum, preferably with minimal resources. Add focus from cryptographic algorithms
CRC=CRC + byte*211 CRC= CRC XOR (CRC SHR 8); // "" , CRC=CRC AND $FF; // 8, 16 - The intermediate CRC for the first action is 16-bit (after calculations it is cut to 8 bits) and in the future we work as with 8-bit, if we have an 8-bit microcontroller, this will speed up data processing.
- We return the high bits and mix with the low bits.
Checking:
Statistics
1: 237
1: 234
1: 241
1: 234
1: 227
1: 238
1: 235
1: 233
1: 231
1: 236
1: 234
1: 241
1: 234
1: 227
1: 238
1: 235
1: 233
1: 231
1: 236
The result is 91% of the theoretical limit. It is quite suitable for use.
If there is no multiplication unit in the microcontroller, you can simulate the multiplication of the operations of addition, offset and XOR. The essence of the process is the same, modified by an error bit, evenly “distributed” over the remaining bits of the checksum.
CRC := (CRC shl 3) + byte; CRC := (CRC shl 3) + byte; CRC:=(CRC XOR (CRC SHR 8)) ; // Result:
Statistics
1: 255
1: 257
1: 255
1: 255
1: 254
1: 255
1: 250
1: 254
1: 256
1: 254
1: 257
1: 255
1: 255
1: 254
1: 255
1: 250
1: 254
1: 256
1: 254
Surprisingly good result. The average value is 254.5 or 99% of the theoretical limit, operations are slightly more, but they are all simple and no multiplication is used.
If for internal storage of intermediate checksum values we give 16 bits to the variable (but only the lower 8 bits are transmitted via the communication line), which is not a problem even for the weakest microcontroller, we will get some improvement in the operation of the algorithm. In general, saving 8 bits does not make much sense, and the 8-bit intermediate variable was previously used simply to simplify the understanding of the algorithm.
Statistics
1: 260
1: 250
1: 252
1: 258
1: 261
1: 255
1: 254
1: 261
1: 264
1: 262
1: 250
1: 252
1: 258
1: 261
1: 255
1: 254
1: 261
1: 264
1: 262
That corresponds to 100.6% of the theoretical limit, quite a good result for such a simple one-line algorithm:
CRC:=CRC + byte*44111; // 16- Full 16-bit multiplication is used. Again, it was not without the magic number 44111 (selected from general considerations without going through the entire subset of numbers). More precisely, it makes sense to select a constant only after having decided on the expected type of errors in the data transmission line.
Such a high result is explained by the fact that 2 cycles of multiplication in a row completely mix the bits, which is what we needed. The exception, it seems, is the last byte of the telegram, especially its high bits, they are not fully mixed in the checksum, but the probability that an error will occur in them is small, approximately 4%. This feature practically does not manifest itself statistically, at least on my set of test data and an error limited to 10 failed bits. To exclude this feature, you can do N + 1 iterations by adding a virtual byte in addition to the ones in the test data block (but this is a complication of the algorithm).
Option without multiplication with the same result. The CRC variable is 16-bit, 8-bit data, the result of the algorithm is the lower 8 bits of the checksum found:
CRC := (CRC shl 2) + CRC + byte; CRC := (CRC shl 2) + CRC + byte; CRC:=(CRC XOR (CRC SHR 8)); The result is 100.6% of the theoretical limit.
The non-multiplication option is simpler, leaving the bare minimum of functions, only 3 mathematical operations:
CRC:=byte + CRC; CRC:=CRC xor (CRC shr 2); The result is 86% of the theoretical limit.
In this case, the loss of the most significant bits is not; they are returned to the lower part of the variable through the XOR function (bit mixer).
A slight improvement in some cases gives the same:
- Double pass on processed data. But at the cost of complicating the algorithm (the outer loop must be specified), at the cost of doubling the processing time.
- The processing of an additional, virtual byte at the end of the processed data, the complexity of the algorithm and the time of the algorithm is almost nonexistent.
- Using a variable to store a checksum greater in bit depth than the final checksum and mixing the lower bits with the high bits.
The result of the work of the considered algorithms, from simple and weak, to complex and qualitative:

16-bit checksum
Further, suppose that 8 bits are not enough for us to form a checksum.

The next option is 16 bits, and the theoretical error probability of the transmitted data is 1: 65536, which is much better. Reliability grows exponentially. But, as a side effect, the amount of auxiliary data is growing, by the example of our telegram, 2 bytes of checksum are added to 8 bytes of useful information.
Simple sum and XOR algorithms, as applied to the 16-bit and subsequent CRCs, are not considered at all, they practically do not improve the quality of work, compared to the 8-bit variants.
We modify the algorithm for processing a checksum of 16 bits, it should be noted that there is also a magic number 8 and 44111, a significant and unreasonable change worsens the work of the algorithm several times.
CRC:=CRC + byte16*44111; // 16- CRC:=CRC XOR (CRC SHR 8); Result:
Statistics
1: 43478
1: 76923
1: 83333
1: 50,000
1: 83333
1: 100,000
1: 90909
1: 47,619
1: 50,000
1: 90909
1: 76923
1: 83333
1: 50,000
1: 83333
1: 100,000
1: 90909
1: 47,619
1: 50,000
1: 90909
That corresponds to 109% of the theoretical limit. There is a measurement error, but it is excusable for 10 million iterations. It also affects the creation algorithm, and in general the type of errors. For a more accurate analysis, in any case, you need to adjust the conditions for errors in a particular data line.
Additionally, I note that you can use 32-bit intermediate variables to accumulate the result, and use the final checksum as the lower 16 bits. In many cases, for any digit of the checksum, the quality of the algorithm improves somewhat.
32-bit checksum
Let's move on to the 32-bit checksum option. There is a problem with the time devoted to the analysis of statistical data, since the number of transmitted telegrams is already comparable to 2 ^ 32. The algorithm is the same; magic numbers change upwards
CRC:=CRC+byte32*$990C9AB5; CRC:=CRC XOR (CRC SHR 16); Over 10 million iterations, no error was detected. To speed up the collection of statistics cut the CRC to 24 bits:
CRC = CRC AND $FFFFFF; The result, out of 10 million iterations, the error was detected 3 times
Statistics
1: 1,000,000
1: no
1: no
1: no
1: 1,000,000
1: no
1: 1,000,000
1: no
1: no
1: no
1: no
1: no
1: no
1: 1,000,000
1: no
1: 1,000,000
1: no
1: no
1: no
Quite a good result and generally close to the theoretical limit for 24-bit checksum (1: 16777216). Here it should be noted that the data integrity control function is evenly distributed across all CRC bits, and it is quite possible to discard them from any side if there is a limit on the size of the transmitted CRC.
For full-fledged 32 bits, it’s enough to wait long for the result, there are simply no errors, for an acceptable waiting time.
Option without multiplication:
CRC := (CRC shl 5) + CRC + byte; CRC := (CRC shl 5) + CRC; CRC:=CRC xor (CRC shr 16); There was no failure for a full-fledged checksum. The checksum trimmed to 24 bits shows approximately the same results, 8 errors per 100 million iterations. Intermediate variable CRC 64-bit.
64-bit checksum
And finally, 64-bit checksum, the maximum checksum, which makes sense when transferring data at the lower level:
CRC:=CRC+byte64*$5FB7D03C81AE5243; CRC:=CRC XOR (CRC SHR 8); // 1..20 Wait for the data transmission error, until the end of the universe, probably will not work :)

A method similar to that used for the CRC32 showed similar results. More bits are left, higher reliability is in full compliance with the theoretical limit. Checked on the lower 20 and 24 bits, this seems to be quite sufficient to assess the quality of the algorithm.
You can also apply for 128-bit numbers (and even larger ones), the main thing is to choose correctly 128-bit magic constants. But this is clearly not for microcontrollers, such numbers are not supported by the compiler.
Comments
In general, the multiplication method is similar to the generation of a pseudo-random sequence, only taking into account the useful data involved in the process.
I recommend to use in microcontrollers, or to check the integrity of any transmitted data. It is a working method, already as it is, despite the simplicity of the algorithm.
My CRC research project on githab .
Further, it would be interesting to optimize the algorithm for more real data (not pseudo-random numbers by the standard algorithm), to select more suitable magic numbers for a number of tasks and initial conditions, I think you can still win fractions of a percent in the quality of the algorithm. Optimize the algorithm for speed, readability of the code (the simplicity of the algorithm), quality of work. Ideally, get and test code samples for all types of microcontrollers, for this you need examples using the multiplication of 8, 16, 32 bit data, and no multiplication at all.
Source: https://habr.com/ru/post/278171/
All Articles