Pathfinding: A simple implementation of a funnel algorithm (Funnel Algorithm)

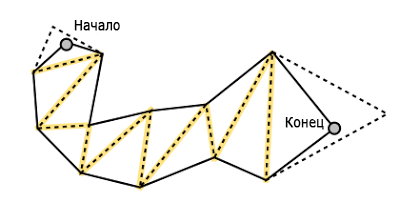
The funnel algorithm is a simple algorithm for finding the simplest path that passes through the “portals”. The most detailed description can be found at the link Efficient Triangulation-Based Pathfinding ( 2 )
Here, this algorithm will be implemented before the stupor is simple. Instead of using queues and other funny things, our simplest implementation restarts the loop every time it detects another angle. This means that some portals will be polled more often than they should, nevertheless, making implementation easier.

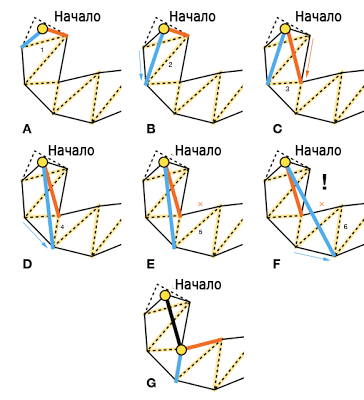
The canvas above shows the 6 steps of this algorithm. On checking each facet of the portal (the ants on something yellow), the following actions are performed:

Check whether the points inside the current tunnel are left and right. If the answer is yes, then we move on without doing anything (AD).
If the new left point is outside the tunnel, the tunnel is not updated (EF)
If the new left point is behind the right side of the tunnel (F), we add the right point of the tunnel as the angle of the path and set and set this (left) point as the starting point and restart the algorithm (G).

These rules apply to the left side.
As can be seen from the example above, some faces are rechecked several times, but all of these calculations are so simple that the overhead is dismissively small, giving a simple and practical implementation.

Badly hidden code

inline float triarea2(const float* a, const float* b, const float* c) { const float ax = b[0] - a[0]; const float ay = b[1] - a[1]; const float bx = c[0] - a[0]; const float by = c[1] - a[1]; return bx*ay - ax*by; } inline bool vequal(const float* a, const float* b) { static const float eq = 0.001f*0.001f; return vdistsqr(a, b) < eq; } int stringPull(const float* portals, int nportals, float* pts, const int maxPts) { //   . int npts = 0; //   float portalApex[2], portalLeft[2], portalRight[2]; int apexIndex = 0, leftIndex = 0, rightIndex = 0; vcpy(portalApex, &portals[0]); vcpy(portalLeft, &portals[0]); vcpy(portalRight, &portals[2]); //   . vcpy(&pts[npts*2], portalApex); npts++; for (int i = 1; i < nportals && npts < maxPts; ++i) { const float* left = &portals[i*4+0]; const float* right = &portals[i*4+2]; //   . if (triarea2(portalApex, portalRight, right) <= 0.0f) { if (vequal(portalApex, portalRight) || triarea2(portalApex, portalLeft, right) > 0.0f) { //  . vcpy(portalRight, right); rightIndex = i; } else { //     ,     ,       vcpy(&pts[npts*2], portalLeft); npts++; //   . vcpy(portalApex, portalLeft); apexIndex = leftIndex; //   vcpy(portalLeft, portalApex); vcpy(portalRight, portalApex); leftIndex = apexIndex; rightIndex = apexIndex; //  i = apexIndex; continue; } } //   . if (triarea2(portalApex, portalLeft, left) >= 0.0f) { if (vequal(portalApex, portalLeft) || triarea2(portalApex, portalRight, left) < 0.0f) { //  . vcpy(portalLeft, left); leftIndex = i; } else { //    ,     ,      . vcpy(&pts[npts*2], portalRight); npts++; //    vcpy(portalApex, portalRight); apexIndex = rightIndex; //   vcpy(portalLeft, portalApex); vcpy(portalRight, portalApex); leftIndex = apexIndex; rightIndex = apexIndex; //  i = apexIndex; continue; } } } //     . if (npts < maxPts) { vcpy(&pts[npts*2], &portals[(nportals-1)*4+0]); npts++; } return npts; }

The portals array contains all the portal portals of the path to be simplified, the first point of the face on the left and the first point of the face on the right. The first right and first left points are our starting point, and the last left and right points are our end point. Those. like that:

 //   vcpy(&portals[nportals*4+0], startPos); vcpy(&portals[nportals*4+2], startPos); nportals++; //     for (int i = 0; i < path->npolys-1; ++i) { getPortalPoints(mesh, path->poly[i], path->poly[i+1], &portals[nportals*4+0], &portals[nportals*4+2]); nportals++; } //   vcpy(&portals[nportals*4+0], endPos); vcpy(&portals[nportals*4+2], endPos); nportals++;

A drop of honey in a barrel of honey is that this algorithm can be implemented in the context of any navigation format. Grid, connected squares, quadtree, waypoints (waypoints) or nesmesh - indifferent, the main thing is that you can provide a list of segments that are portals from one node to another.

The algorithm is also well combined with the stirring. You are free to calculate the desired speed of movement, based on the following turns. It is so fast that you can count it (speed) on each iteration before applying the step of striing.
')
ps It is highly recommended to get acquainted with a more complete version - at least diagonally (from a translator).

Source: https://habr.com/ru/post/278151/

All Articles

Pathfinding: A simple implementation of a funnel algorithm (Funnel Algorithm)

More articles: