DIY: SQL JOIN in Java
I often interview the developers and often ask them a simple, like a sledgehammer, question - how does the JOIN work in SQL inside? In response, I usually hear an incoherent moo about magic trees and indexes that are faster. Once it seemed to me that every specialist programmer should know what he is working with. Subsequently, life explained to me that this is not so. But I still don’t understand how I can pull the bazonok for years without even realizing, but what is there under her hood?
Let's spend an educational program and together we will look, how these joins work , and even we realize a couple of algorithms.
For people who claim that they worked a lot with SQL, I ask this kind of task during interviews.
There is a SQL command
You need to do the same in Java, i.e. implement method
I am not asking you to directly code the implementation, but I am waiting for at least a verbal explanation of the algorithm.
')
Additionally, I ask what needs to be changed in the signature and implementation to pretend that we are working with indexes.
Let's first understand, why should we even think about joining devices?
The most basic algorithm for combining two lists is now taking place in schools. The point is very simple - for each element of the first list, go through all the elements of the second list; if the keys of the elements suddenly turned out to be equal, we write the coincidence in the resulting table. To implement this algorithm, two nested loops are sufficient, which is why it is called this.
The main advantage of this method is complete indifference to the input data. The algorithm works for any two tables, does not require any indexes and data shifting in memory, and is also simple to implement. In practice, this means that it is enough just to run on the disk with two cursors and periodically spit out matches in the socket.
However, the fatal minus of the algorithm is the high time complexity of O (N * M) (quadratic asymptotics, if you know what I mean). For example, for a pair of small tables with 100k and 500k records, you need to do as many as 100.000 * 500.000 = 50.000.000.000 (50 billion) comparison operations. Requests with such a joyno will be performed impolitely for a long time, often they are the cause of the merciless brakes of self-signed CMS logs.
Modern RDBMS use nested loops join in the most hopeless cases when it is not possible to apply any optimization.
UPD. zhekappp and potapuff correct that nested loops are effective for a small number of lines, when deploying any optimization is more expensive than just running through a nested loop. There is a class of systems for which this is relevant.
If the size of one of the tables allows you to shove it entirely into memory, then you can make a hash table based on it and quickly search for the necessary keys in it. Let's talk a little more.
Check the size of both lists. Take the smaller of the lists, read it fully and load it into memory by building a HashMap. Now back to the larger list and move the cursor over it from the beginning. For each key, check to see if it is the same in the hash table. If there is - write a match in the resulting table.
The time complexity of this algorithm falls to linear O (N + M), but additional memory is required.
What is important, at the time of dinosaurs, it was believed that the right table should be loaded into memory, and iterated on the left. Normal RDBMS now has cardinality statistics, and they themselves determine the join order, but if for some reason the statistics is not available, then the right table is loaded into memory. This is important to remember when working with young clumsy tools like Cloudera Impala.
Now imagine that the data in both lists are pre-sorted, for example, in ascending order. This happens if we had indexes on these tables, or if we sorted the data in the previous stages of the query. As you probably remember, two sorted lists can be glued together into one sorted for linear time - this is the basis of the merge sort algorithm. Here we have a similar task, but instead of sticking lists, we will look for common elements in them.
So, put the cursor on the top of both lists. If the keys under the cursors are equal, write the match in the resulting table. If not, we look under which of the cursors the key is smaller. Move the cursor over the smaller key one forward, thereby “catching up” with another cursor.
If the data is sorted, then the time complexity of the algorithm is linear O (M + N) and no additional memory is required. If the data is not sorted, you must first sort it. Because of this, the time complexity increases to O (M log M + N log N), plus additional memory requirements appear.
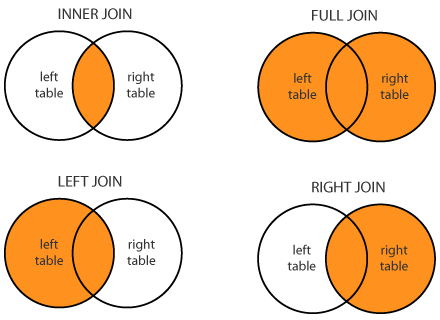
You may have noticed that the code written above simulates only INNER JOIN, and it counts that all the keys in both lists are unique, i.e. occur no more than once. I did so specifically for two reasons. Firstly, it is more obvious - the code contains only the logic of the joins themselves and nothing superfluous. And secondly, I really wanted to sleep. But nevertheless, let's at least discuss what needs to be changed in the code to support different types of joins and non-unique key values.
The first problem is non-unique, i.e. duplicate keys For duplicate keys, you need to generate a Cartesian product of all the corresponding values.
In Nested Loops Join for some reason it works right away.
In Hash Join you have to replace HashMap with MultiHashMap.
For Merge Join, the situation is much more sad - you have to remember how many elements with the same key we saw.
Working with non-unique keys increases the asymptotics to O (N * m + M * n), where n and m is the average of records per key in the tables. In the degenerate case, when n = N and m = M, the operation turns into a CROSS JOIN.
The second problem - you need to keep track of the keys for which there was no pair.
For Merge Join, a key without a pair is visible at once for all JOIN directions.
For Hash Join, you can immediately see the lack of corresponding keys with the join on the left. In order to fix unpaired keys on the right, you will have to set up a separate “there is a pair!” Flag for each element of the hash table. After the main join is complete, you will have to go through the entire hash table and add keys without the pair flag to the result.
For Nested Loops Join, the situation is similar, and everything is so simple that I even mastered this code:
If you read this far, it means that the article seemed interesting to you. So, you forgive me a small portion of moralizing.
I really believe that knowledge of the RDBMS at the SQL level is absolutely not enough to consider myself a professional software developer. A professional should know not only his code, but also an exemplary arrangement of stack neighbors, i.e. 3rd-party systems he uses - databases, frameworks, network protocols, file systems. Without this, the developer degenerates to a coder or computer operator, and in truly complex, large-scale tasks, it becomes useless.
UPD. Despite this afterword, the article is, in fact, about JOINs.
Disclaimer: Actually, I promised another article about Scalding, but the previous one did not arouse much interest from the public. Because of this, the topic was decided to change.
Let's spend an educational program and together we will look, how these joins work , and even we realize a couple of algorithms.

Formulation of the problem
For people who claim that they worked a lot with SQL, I ask this kind of task during interviews.
There is a SQL command
SELECT left.K, left.V1, right.V2 FROM left JOIN right ON left.K = right.K; You need to do the same in Java, i.e. implement method
<K, V1, V2> List<Triple<K, V1, V2>> join(List<Pair<K, V1>> left, List<Pair<K, V2>> right); I am not asking you to directly code the implementation, but I am waiting for at least a verbal explanation of the algorithm.
')
Additionally, I ask what needs to be changed in the signature and implementation to pretend that we are working with indexes.
Let's first understand, why should we even think about joining devices?
- Knowing the theory is useful for purely cognitive reasons.
- If you distinguish between types of joins, then the query execution plan, which is obtained by the EXPLAIN command, no longer looks to you as a collection of incomprehensible English words. You can see potentially slow spots in the plan and optimize the query by rewriting or hinting.
- In modern analytic tools on top of Hadoop, the query scheduler is a bit stupid (see Cloudera Impala), or there is none at all (see Twitter Scalding, Spark RDD). In the latter case, you have to collect the request manually from primitive operations.
Finally, there is a risk that one day you will get an interview with me or another bore.But in fact, the article is not about interviews, but about the JOIN operation.
Nested loops join
The most basic algorithm for combining two lists is now taking place in schools. The point is very simple - for each element of the first list, go through all the elements of the second list; if the keys of the elements suddenly turned out to be equal, we write the coincidence in the resulting table. To implement this algorithm, two nested loops are sufficient, which is why it is called this.
public static <K, V1, V2> List<Triple<K, V1, V2>> nestedLoopsJoin(List<Pair<K, V1>> left, List<Pair<K, V2>> right) { List<Triple<K, V1, V2>> result = new ArrayList<>(); for (Pair<K, V1> leftPair: left) { for (Pair<K, V2> rightPair: right) { if (Objects.equals(leftPair.k, rightPair.k)) { result.add(new Triple<>(leftPair.k, leftPair.v, rightPair.v)); } } } return result; } The main advantage of this method is complete indifference to the input data. The algorithm works for any two tables, does not require any indexes and data shifting in memory, and is also simple to implement. In practice, this means that it is enough just to run on the disk with two cursors and periodically spit out matches in the socket.
However, the fatal minus of the algorithm is the high time complexity of O (N * M) (quadratic asymptotics, if you know what I mean). For example, for a pair of small tables with 100k and 500k records, you need to do as many as 100.000 * 500.000 = 50.000.000.000 (50 billion) comparison operations. Requests with such a joyno will be performed impolitely for a long time, often they are the cause of the merciless brakes of self-signed CMS logs.
Modern RDBMS use nested loops join in the most hopeless cases when it is not possible to apply any optimization.
UPD. zhekappp and potapuff correct that nested loops are effective for a small number of lines, when deploying any optimization is more expensive than just running through a nested loop. There is a class of systems for which this is relevant.
Hash join
If the size of one of the tables allows you to shove it entirely into memory, then you can make a hash table based on it and quickly search for the necessary keys in it. Let's talk a little more.
Check the size of both lists. Take the smaller of the lists, read it fully and load it into memory by building a HashMap. Now back to the larger list and move the cursor over it from the beginning. For each key, check to see if it is the same in the hash table. If there is - write a match in the resulting table.
The time complexity of this algorithm falls to linear O (N + M), but additional memory is required.
public static <K, V1, V2> List<Triple<K, V1, V2>> hashJoin(List<Pair<K, V1>> left, List<Pair<K, V2>> right) { Map<K, V2> hash = new HashMap<>(right.size()); for (Pair<K, V2> rightPair: right) { hash.put(rightPair.k, rightPair.v); } List<Triple<K, V1, V2>> result = new ArrayList<>(); for (Pair<K, V1> leftPair: left) { if (hash.containsKey(leftPair.k)) { result.add(new Triple<>(leftPair.k, leftPair.v, hash.get(leftPair.k))); } } return result; } What is important, at the time of dinosaurs, it was believed that the right table should be loaded into memory, and iterated on the left. Normal RDBMS now has cardinality statistics, and they themselves determine the join order, but if for some reason the statistics is not available, then the right table is loaded into memory. This is important to remember when working with young clumsy tools like Cloudera Impala.
Merge join
Now imagine that the data in both lists are pre-sorted, for example, in ascending order. This happens if we had indexes on these tables, or if we sorted the data in the previous stages of the query. As you probably remember, two sorted lists can be glued together into one sorted for linear time - this is the basis of the merge sort algorithm. Here we have a similar task, but instead of sticking lists, we will look for common elements in them.
So, put the cursor on the top of both lists. If the keys under the cursors are equal, write the match in the resulting table. If not, we look under which of the cursors the key is smaller. Move the cursor over the smaller key one forward, thereby “catching up” with another cursor.
public static <K extends Comparable<K>, V1, V2> List<Triple<K, V1, V2>> mergeJoin( List<Pair<K, V1>> left, List<Pair<K, V2>> right ) { List<Triple<K, V1, V2>> result = new ArrayList<>(); Iterator<Pair<K, V1>> leftIter = left.listIterator(); Iterator<Pair<K, V2>> rightIter = right.listIterator(); Pair<K, V1> leftPair = leftIter.next(); Pair<K, V2> rightPair = rightIter.next(); while (true) { int compare = leftPair.k.compareTo(rightPair.k); if (compare < 0) { if (leftIter.hasNext()) { leftPair = leftIter.next(); } else { break; } } else if (compare > 0) { if (rightIter.hasNext()) { rightPair = rightIter.next(); } else { break; } } else { result.add(new Triple<>(leftPair.k, leftPair.v, rightPair.v)); if (leftIter.hasNext() && rightIter.hasNext()) { leftPair = leftIter.next(); rightPair = rightIter.next(); } else { break; } } } return result; } If the data is sorted, then the time complexity of the algorithm is linear O (M + N) and no additional memory is required. If the data is not sorted, you must first sort it. Because of this, the time complexity increases to O (M log M + N log N), plus additional memory requirements appear.
Outer joins
You may have noticed that the code written above simulates only INNER JOIN, and it counts that all the keys in both lists are unique, i.e. occur no more than once. I did so specifically for two reasons. Firstly, it is more obvious - the code contains only the logic of the joins themselves and nothing superfluous. And secondly, I really wanted to sleep. But nevertheless, let's at least discuss what needs to be changed in the code to support different types of joins and non-unique key values.
The first problem is non-unique, i.e. duplicate keys For duplicate keys, you need to generate a Cartesian product of all the corresponding values.
In Nested Loops Join for some reason it works right away.
In Hash Join you have to replace HashMap with MultiHashMap.
For Merge Join, the situation is much more sad - you have to remember how many elements with the same key we saw.
Working with non-unique keys increases the asymptotics to O (N * m + M * n), where n and m is the average of records per key in the tables. In the degenerate case, when n = N and m = M, the operation turns into a CROSS JOIN.
The second problem - you need to keep track of the keys for which there was no pair.
For Merge Join, a key without a pair is visible at once for all JOIN directions.
For Hash Join, you can immediately see the lack of corresponding keys with the join on the left. In order to fix unpaired keys on the right, you will have to set up a separate “there is a pair!” Flag for each element of the hash table. After the main join is complete, you will have to go through the entire hash table and add keys without the pair flag to the result.
For Nested Loops Join, the situation is similar, and everything is so simple that I even mastered this code:
public static <K, V1, V2> List<Triple<K, V1, V2>> nestedLoopsJoin( List<Pair<K, V1>> left, List<Pair<K, V2>> right, JoinType joinType ) { // , BitSet rightMatches = new BitSet(right.size()); List<Triple<K, V1, V2>> result = new ArrayList<>(); for (Pair<K, V1> leftPair: left) { // , boolean match = false; for (ListIterator<Pair<K, V2>> iterator = right.listIterator(); iterator.hasNext(); ) { Pair<K, V2> rightPair = iterator.next(); if (Objects.equals(leftPair.k, rightPair.k)) { result.add(new Triple<>(leftPair.k, leftPair.v, rightPair.v)); // match = true; rightMatches.set(iterator.previousIndex(), true); } } // if ((joinType == JoinType.LEFT || joinType == JoinType.FULL) && !match) { result.add(new Triple<>(leftPair.k, leftPair.v, null)); } } // if (joinType == JoinType.RIGHT || joinType == JoinType.FULL) { for (int i = 0; i < right.size(); ++i) { if (!rightMatches.get(i)) { Pair<K, V2> rightPair = right.get(i); result.add(new Triple<>(rightPair.k, null, rightPair.v)); } } } return result; } Moralizing afterword
If you read this far, it means that the article seemed interesting to you. So, you forgive me a small portion of moralizing.
I really believe that knowledge of the RDBMS at the SQL level is absolutely not enough to consider myself a professional software developer. A professional should know not only his code, but also an exemplary arrangement of stack neighbors, i.e. 3rd-party systems he uses - databases, frameworks, network protocols, file systems. Without this, the developer degenerates to a coder or computer operator, and in truly complex, large-scale tasks, it becomes useless.
UPD. Despite this afterword, the article is, in fact, about JOINs.
Additional materials
- Luxurious article about device RDBMS
- Luxury book about algorithms . It is useful to look through before the interview.
Disclaimer: Actually, I promised another article about Scalding, but the previous one did not arouse much interest from the public. Because of this, the topic was decided to change.
Source: https://habr.com/ru/post/278087/
All Articles