How 3D robot scans
There are many 3D scanning technologies in the world. On the basis of each of them created dozens of scanner models. Some scanners can scan only small objects, some are designed to scan people. Others can scan a house or room. The mere enumeration of various variations of scanners would take an entire article.
In this article I will talk about one of the promising areas of scanning - about how robotic 3D scanners are made.

3D scanning of an object is not an instant process. It requires a person to make a constant analysis of the current situation and, depending on the results, the adjustment of their actions. Scanning large objects may take some time.
Examples can be found here and here .
If you need to scan a lot of objects (for example, to solve the problem of quality control or to digitize the assortment of a store), then the best way is to rid yourself of the routine and use a robot. Maybe this does not greatly accelerate the process, but it makes the result stable, repeatable and eliminates the operator from physical labor.
(Actually, the main argument is of course: because it’s cool! Human-like robots and everything!)

When a person scans, he sees everything: what is scanned is bad, what is not to the end, where there is a hole in the scanned object. The eyes are an independent scanner that allows you to check the quality of the incoming data and say “AHA! Here you haven't watched! ” But when the robot scans, such decisions must be made by him. And the only information for making such decisions is the data obtained from the scanner. And the data often looks like this:


Here is the result of what happens if you scan for 15-20 seconds near the object.
When scanning, all scanners give out either a cloud of points, or a cloud of polygons, or a depth map. Any kind of information may contain holes. Holes can appear for a variety of reasons:
But the robot scanner does not know the reasons. He does not know whether the object has ended, or if it is glare. The robot has no independent controls. He learns the world around only through a scanner.
')
The first and easiest way is to collect an excess amount of data or simply try to scan the object from all possible sides. For example, like this:
This approach has a number of disadvantages:

(a frame from the video above, you can see errors inside the sleeve)
The second approach is a pre-calculated trajectory. Of course, this can be done only in a limited number of scenarios, when the shape of the object is approximately known. For example, in production for solving the problem of quality control of the manufactured product.
The third, the most reasonable and interesting way - depending on the observed object, select the minimum number of species and the optimal trajectory of hand movement with the scanner in such a way as to achieve maximum coverage of the object.
Based on the received data, a closed surface is constructed. After that, areas for which the lowest accuracy is observed iteratively are observed (there is a surface, but there are no points confirming it). Observe the region -> recalculate the model -> observe the region. The result is a series of consecutive scans as a result of which the robot “knows” the object.

The case remains for the small: take the math, which will allow to build the surface. Add a module to assess the reliability of the constructed surface. Run in a loop.
The most interesting and beautiful mathematics that solves the problem of constructing a surface from incomplete data is “Poisson recovery”. The main assumption is that we consider one object. Then we can imagine the “hidden” function f (p) from a position in space. A positive value is outside the object, a negative is inside. On the desired surface of the object function will be zero.

It is clear that the gradient of f (p) on the surface is the vector of the normal to the desired surface of the object.
When processing the primary data from the scanner, we already estimate the normals to the scanned surface. Then the input data for the search for the function f (p) will be a set of points in space and normal to the surface of the object at these points: (p, n) i Usually, when scanning a less complex object, there are hundreds of thousands of such points.
The meaning of this function f (p) and normals is easiest to understand in 2D. On the left, normals to a 2D object, on the right, the value of the function f (shown by the third coordinate), blue color outside the object, orange color inside.

Points (p, n) i lie on the surface. Ideally:

where the inverted triangle is the Nabla operator (gradient vector).
Naturally, the normals in the points and the positions of the points themselves contain measurement errors, so there is no such function f, and you should not look for it. In this situation, the normal field v (x) is introduced and requires a minimum:

This minimization problem is solved just by using the Poisson equation:

Who is interested in reading in more detail about the conclusion and mathematics: the article of the author who invented the method.
And having solved this equation (there are many ways to solve the problem, but you have to go, of course, to a difference problem, and then to a huge linear equation), you need to find an isosurface with zero f, and use a marching cube algorithm to build a polygonal model.
Here, by the way, several problems appear at once, which have to be overcome:
But from all other sides this mathematical approach is good and reliably applicable in reality (although not a quick calculation process).
The only thing is Since the density of points p i in space is very variable, it is advisable to split the entire volume using an octree and solve the resulting difference equation taking into account the division into cubes of different sizes.

You can either set the smallest splitting level, or split up the space until no more than one point with the normal remains in each cell. As a result, the number of cubes will be comparable to the number of points obtained during scanning.
There is another approach proposed by F. Calakli and G. Taubin in 2011, which gives the same qualitative result, and under certain conditions is even better than the method with solving the Poisson equation, but is somewhat more accessible for understanding and programming. In Wikipedia, these two methods are simply confused .
Similarly, we look for the function f (p), which is negative inside the object, and positive outside it. In the same way, we want to bring the f (p) gradient closer to the normals in the given positions that we got during the scan. But we will look for a minimum:

It looks rather cumbersome, but in reality we only ask that the function at the points of Pi would be smaller (the first term), so that its gradient is closer to the normals at the same points (the second term), and that in the whole volume it has second derivatives were smaller, more precisely - the Hessian of function (third member). The requirement for second derivatives is quite important, since I want very much that, having gone beyond the boundaries of the object, the function does not start oscillating, and such nightmarish pictures fail:

Those. everything was minimized, but having gone away from the points that we measured with the scanner, the function f (p) did not behave arbitrarily.
And note that each member is a square. This is not just because just for quadratic forms, it is easy to analytically obtain an extremum (for the forms A * A-2 * b * A + c, the local minimum at the point A = b). Just write everything in a differential form, i.e. Let us replace the partial derivatives on the difference on the borders of small cubes, and then in the matrix, in order to use the focus with a minimum of square shape. As a result, we obtain a linear system of equations, the unknown in which are the values of the function f (p) inside the cubes. And the cubes, as well as in the method of reconstruction described above, are worth taking unevenly, and building an octree tree. Who is interested in a detailed conclusion, the text of the article.
It works in the same way as the method based on the Poisson equation. There is one small advantage in that it is not necessary to "smear" the normals in space in order to be able to get the divergence from the vector field of normals, while losing accuracy and unnecessarily smoothing the object. On the other hand, if the scanner rather roughly evaluates the normals, then this advantage can be a disadvantage of the method.
By itself, the Poisson algorithm does not tell us what is visible and what is not. We need to come up with some measure of quality to assess the reliability of the result. The simplest measure is to walk along the surface in small cubes and see how many dots there are in each of them:

The more points - the more confidence, the more red. Such a measure of quality will be very representative. Indeed, we cannot trust areas where we have not seen anything. And if they saw, then, probably, there really is something.
Now everything seems to be clear. We need to select such points for further scanning, from which to make the next series of frames, which should be frozen into the main model.
To do this, we mark out the surrounding space. We will check each of its points by determining how many invalid points of the figure we will see from it. The more such points - the more profitable to watch.
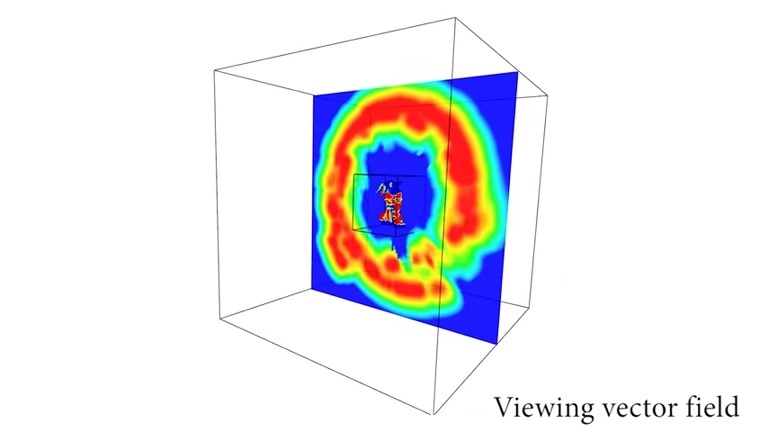
It remains to find local maxima and launch observations:

Then again Poisson is performed, then again an additional scan is performed. And so on a circle, until the finished model appears.
Maybe you can scan well, so that everything was and so? Why complicate a bunch of math? Here is a simple example. Three pictures. The 3D scan was made by an Artec Spider scanner . The first - the raw information from the scanner, in fact a cloud of points. The second is the Fusion algorithm, which simply does averaging and position control. The third is the Poisson algorithm. And the difference is in the face!



And so this dragon will look whole:

As a result, the robot's surface scanning algorithm looks like this:

In more detail about such a scanning scheme can be read, for example, here .
Or see how this whole thing works:
PS The robot in the video turns his head just like that, it has nothing to do with scanning
PSS Thanks to Vasyutka for the help in writing the article and the Artek team for numerous edits and bringing to mind!
In this article I will talk about one of the promising areas of scanning - about how robotic 3D scanners are made.

Why do you need it?
3D scanning of an object is not an instant process. It requires a person to make a constant analysis of the current situation and, depending on the results, the adjustment of their actions. Scanning large objects may take some time.
Examples can be found here and here .
If you need to scan a lot of objects (for example, to solve the problem of quality control or to digitize the assortment of a store), then the best way is to rid yourself of the routine and use a robot. Maybe this does not greatly accelerate the process, but it makes the result stable, repeatable and eliminates the operator from physical labor.

The main difference and complexity of the process
When a person scans, he sees everything: what is scanned is bad, what is not to the end, where there is a hole in the scanned object. The eyes are an independent scanner that allows you to check the quality of the incoming data and say “AHA! Here you haven't watched! ” But when the robot scans, such decisions must be made by him. And the only information for making such decisions is the data obtained from the scanner. And the data often looks like this:


Here is the result of what happens if you scan for 15-20 seconds near the object.
When scanning, all scanners give out either a cloud of points, or a cloud of polygons, or a depth map. Any kind of information may contain holes. Holes can appear for a variety of reasons:
- There may indeed be a hole in the object.
- The object has a recess. Sometimes the scanner simply cannot look inside: the base between the “eyes” is too big
- If a scan is performed by radiation at a certain frequency, and inside the area there is a material that absorbs radiation at a given frequency (or specular reflection), then again there will be a hole
- If the scan is a passive scanner with two cameras, and the area is monotonous, then ... well, you already understood
- A large angle on the scan plane to the scanner can also cause a tear
- The hole will be if you can not scan from the "hole". For example, the base of the statue or the back side of the statue standing close to the wall (it happened)
- I'm sure you can think of more cases.
But the robot scanner does not know the reasons. He does not know whether the object has ended, or if it is glare. The robot has no independent controls. He learns the world around only through a scanner.
')
How to fight?
The first and easiest way is to collect an excess amount of data or simply try to scan the object from all possible sides. For example, like this:
This approach has a number of disadvantages:
- Scanning time is pretty long. You have to twist the object for a long time.
- In the case of simple forms (a la beer cans), everything will be fine, but as soon as we try to scan something rather complicated with a large number of “undercuts”, it turns out that many unscanned zones remain.
- Not the fact that all the provisions will be passed. For example, to see some point inside the object, you need to look strictly from one side to within a couple of degrees, and to pass all 2πR 2 ≈ 41253 square degrees is unrealistic (even if the cut off half-plane ≈20k)

(a frame from the video above, you can see errors inside the sleeve)
The second approach is a pre-calculated trajectory. Of course, this can be done only in a limited number of scenarios, when the shape of the object is approximately known. For example, in production for solving the problem of quality control of the manufactured product.
The third, the most reasonable and interesting way - depending on the observed object, select the minimum number of species and the optimal trajectory of hand movement with the scanner in such a way as to achieve maximum coverage of the object.
Based on the received data, a closed surface is constructed. After that, areas for which the lowest accuracy is observed iteratively are observed (there is a surface, but there are no points confirming it). Observe the region -> recalculate the model -> observe the region. The result is a series of consecutive scans as a result of which the robot “knows” the object.
The case remains for the small: take the math, which will allow to build the surface. Add a module to assess the reliability of the constructed surface. Run in a loop.
Poisson reconstruction
The most interesting and beautiful mathematics that solves the problem of constructing a surface from incomplete data is “Poisson recovery”. The main assumption is that we consider one object. Then we can imagine the “hidden” function f (p) from a position in space. A positive value is outside the object, a negative is inside. On the desired surface of the object function will be zero.
It is clear that the gradient of f (p) on the surface is the vector of the normal to the desired surface of the object.
When processing the primary data from the scanner, we already estimate the normals to the scanned surface. Then the input data for the search for the function f (p) will be a set of points in space and normal to the surface of the object at these points: (p, n) i Usually, when scanning a less complex object, there are hundreds of thousands of such points.
The meaning of this function f (p) and normals is easiest to understand in 2D. On the left, normals to a 2D object, on the right, the value of the function f (shown by the third coordinate), blue color outside the object, orange color inside.
Points (p, n) i lie on the surface. Ideally:

where the inverted triangle is the Nabla operator (gradient vector).
Naturally, the normals in the points and the positions of the points themselves contain measurement errors, so there is no such function f, and you should not look for it. In this situation, the normal field v (x) is introduced and requires a minimum:

This minimization problem is solved just by using the Poisson equation:

Who is interested in reading in more detail about the conclusion and mathematics: the article of the author who invented the method.
And having solved this equation (there are many ways to solve the problem, but you have to go, of course, to a difference problem, and then to a huge linear equation), you need to find an isosurface with zero f, and use a marching cube algorithm to build a polygonal model.
Here, by the way, several problems appear at once, which have to be overcome:
- The field v (x) is a field of normals, in fact, it is not somewhat differentiated, and, therefore, it is necessary to “smear” them somehow in space. In other words - to dream.
- Solution of the Poisson problem up to a constant. And we need to find the surface of the object, so we have to solve another optimization problem in order to minimize the values of the function f at all points p i .
But from all other sides this mathematical approach is good and reliably applicable in reality (although not a quick calculation process).
The only thing is Since the density of points p i in space is very variable, it is advisable to split the entire volume using an octree and solve the resulting difference equation taking into account the division into cubes of different sizes.

You can either set the smallest splitting level, or split up the space until no more than one point with the normal remains in each cell. As a result, the number of cubes will be comparable to the number of points obtained during scanning.
Smooth Signed Distance Surface Reconstruction (almost Poisson Reconstruction)
There is another approach proposed by F. Calakli and G. Taubin in 2011, which gives the same qualitative result, and under certain conditions is even better than the method with solving the Poisson equation, but is somewhat more accessible for understanding and programming. In Wikipedia, these two methods are simply confused .
Similarly, we look for the function f (p), which is negative inside the object, and positive outside it. In the same way, we want to bring the f (p) gradient closer to the normals in the given positions that we got during the scan. But we will look for a minimum:

It looks rather cumbersome, but in reality we only ask that the function at the points of Pi would be smaller (the first term), so that its gradient is closer to the normals at the same points (the second term), and that in the whole volume it has second derivatives were smaller, more precisely - the Hessian of function (third member). The requirement for second derivatives is quite important, since I want very much that, having gone beyond the boundaries of the object, the function does not start oscillating, and such nightmarish pictures fail:

Those. everything was minimized, but having gone away from the points that we measured with the scanner, the function f (p) did not behave arbitrarily.
And note that each member is a square. This is not just because just for quadratic forms, it is easy to analytically obtain an extremum (for the forms A * A-2 * b * A + c, the local minimum at the point A = b). Just write everything in a differential form, i.e. Let us replace the partial derivatives on the difference on the borders of small cubes, and then in the matrix, in order to use the focus with a minimum of square shape. As a result, we obtain a linear system of equations, the unknown in which are the values of the function f (p) inside the cubes. And the cubes, as well as in the method of reconstruction described above, are worth taking unevenly, and building an octree tree. Who is interested in a detailed conclusion, the text of the article.
It works in the same way as the method based on the Poisson equation. There is one small advantage in that it is not necessary to "smear" the normals in space in order to be able to get the divergence from the vector field of normals, while losing accuracy and unnecessarily smoothing the object. On the other hand, if the scanner rather roughly evaluates the normals, then this advantage can be a disadvantage of the method.
Measure of quality
By itself, the Poisson algorithm does not tell us what is visible and what is not. We need to come up with some measure of quality to assess the reliability of the result. The simplest measure is to walk along the surface in small cubes and see how many dots there are in each of them:

The more points - the more confidence, the more red. Such a measure of quality will be very representative. Indeed, we cannot trust areas where we have not seen anything. And if they saw, then, probably, there really is something.
Selection of further scanning direction
Now everything seems to be clear. We need to select such points for further scanning, from which to make the next series of frames, which should be frozen into the main model.
To do this, we mark out the surrounding space. We will check each of its points by determining how many invalid points of the figure we will see from it. The more such points - the more profitable to watch.

It remains to find local maxima and launch observations:

Then again Poisson is performed, then again an additional scan is performed. And so on a circle, until the finished model appears.
Does Poisson need it at all?
Maybe you can scan well, so that everything was and so? Why complicate a bunch of math? Here is a simple example. Three pictures. The 3D scan was made by an Artec Spider scanner . The first - the raw information from the scanner, in fact a cloud of points. The second is the Fusion algorithm, which simply does averaging and position control. The third is the Poisson algorithm. And the difference is in the face!



And so this dragon will look whole:

Putting it all together
As a result, the robot's surface scanning algorithm looks like this:
- Making the primary scan
- Build according to the available information approximating surface
- We build a measure of the quality of the surface
- Selecting points for further scanning
- If the points are of great importance - make a scan and go to step 2
- If there is almost no information added when scanning, give the user a final scan
In more detail about such a scanning scheme can be read, for example, here .
Or see how this whole thing works:
PS The robot in the video turns his head just like that, it has nothing to do with scanning
PSS Thanks to Vasyutka for the help in writing the article and the Artek team for numerous edits and bringing to mind!
Source: https://habr.com/ru/post/277885/
All Articles