The benefits of big data technology in everyday life

Among many researchers and developers there is an opinion that big data processing tools in the field of machine learning are often redundant - you can always sample, tune in memory and use your favorite R, Python and Matlab. But in practice, there are problems when even a relatively small amount of data, the size of a couple of gigabytes, is difficult to handle in this style - and this is where the “big data” technologies can help.

A good illustrative example of such a task is the task of our SNA Hakathon 2016 competition: a social graph of one million users and their demography is given. The task is to find hidden links in this column . The size of the graph provided is only two gigabytes in GZip and, it would seem, the application of big data technologies is not justified here, but this is only at first glance.
')
One of the most important “features” in the task of searching for hidden connections in a social graph is the number of mutual friends. And in terms of design, this is a very heavy “feature” - the number of nodes between which there are paths of length 2 is several orders of magnitude larger than the number of direct links in the graph. As a result, in the calculation, the graph “explodes” and turns from a sparse matrix of two gigabytes into a dense terabyte matrix .

It would seem that to solve this problem it’s time to lift a small cluster, but you shouldn’t hurry: having adopted the principles of big data processing and the corresponding technologies, the task can be solved on a regular laptop. We take “divide and conquer” and “cut tails at once” from the principles, and Apache Spark as a tool.

What is the problem?

The graph opened for analysis is represented as an adjacency list (a list of neighbors is given for each vertex) and is asymmetric (outgoing arcs are not known for all vertices). The obvious way to calculate the number of common friends between the vertices in this column is as follows:

1. We translate the graph into a list of pairs;
2. Join them to a list of couples to themselves for a "mutual friend"
3. Sum the number of occurrences of each pair.

The advantages of this approach, of course, should be attributed to the simplicity - on the Spark this solution will take 5 lines. But he has more minuses. Already in the second step, when implementing join-a, a shuffle occurs (sending data between different processing steps), which will very quickly exhaust local storage resources. And if suddenly there is enough space for it on your laptop, then it will definitely not be enough for shuffle in the third stage.

To cope with the task, you need to break it into parts ("divide and conquer") and filter the results with a small number of mutual friends ("cut tails at once"). But to fulfill both conditions at once is problematic - when calculating the number of mutual friends only for a part of the graph, we get an incomplete picture and cannot adequately apply the filter ...

Where is the solution?

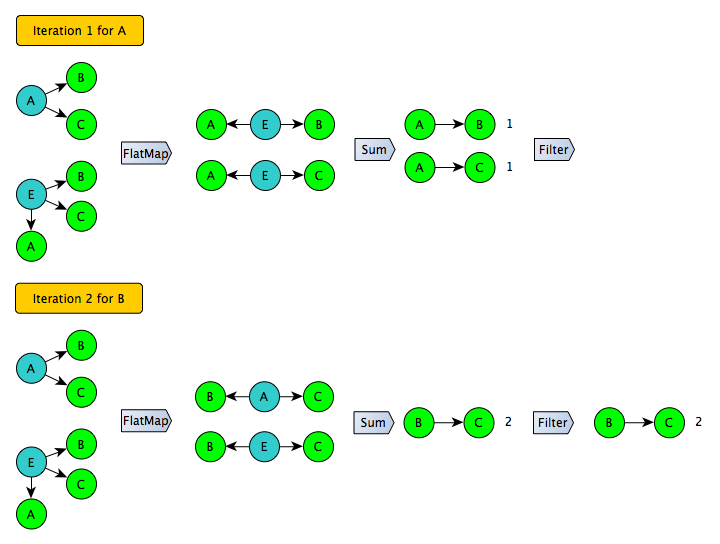
Let's try to look at the problem from the other side. Most troubles are the join of the list of pairs in the second stage: the format of the list of pairs itself is inefficient in terms of size, and one of the sides of the join cannot be filtered without distorting the result. Is it possible to do without converting to the list of pairs and join-a? Yes, if you use the principle "I am a mutual friend for my two friends." In this case, we iterate over the adjacency list for each of the friends list and generate all pairs, and then count how many times each pair appeared in the whole system - as a result, the problem is solved using one shuffle :)

Developing this idea, it is easy to take the next step: instead of generating all possible pairs, it is necessary to generate only pairs for a certain subset of users on the left side (for example, with even identifiers). Then this procedure can be repeated several times and get a full coverage. Moreover, at each iteration, you can safely apply the filter to cut off the “long tail” - for users in this subset, the numbers are obtained exactly.

This approach works well for a symmetric graph, but the graph presented at SNA Hakathon 2016 is asymmetric — for some users, only incoming arcs are known. To use this trick, the graph must first be expanded:



The result of the conversion can already be saved and used as an input for the iterative algorithm:

Is the game worth the candle?

It was on this graph that the counting of the number of common friends "head on" took 1 hour on a cluster of 100 servers. The optimized iterative version worked in 4 and a half hours on one dual-core laptop. These figures allow us to conclude that the “head-on” option is acceptable only for fairly large firms and / or research teams, whereas the optimized version can be run by almost anyone. In addition, all the necessary code and instructions are published in the public domain on GitHub .

Is this “big data technology” really necessary in this scheme? Is it possible to repeat the same in R or Python? In theory, nothing is impossible. But in practice, the implementation will have to solve a large number of problems and get acquainted with many very specific packages and functions. The resulting code will be larger and clearly more expensive to develop and maintain.

In fact, even if we abstract from this example, using Apache Spark in many cases may be preferable to R and Python: for Spark, parallel data processing is natural, which provides a higher speed, with almost no changes, the code can be transferred to a cluster in Google Cloud ( case study ) and applied to a significantly larger amount of data. But the collection of supported machine learning algorithms, although still inferior to the “ancestors”, is already quite impressive and constantly updated ( MLLib ).

Time to learn Scala :)