Evaluation and optimization of computing performance on multi-core systems

This publication is a translation of the first part of the article Characterization and Optimization Methodology of Applied to Stencil Computations of Intel engineers. This part is devoted to analyzing the performance and building a roofline model on the example of a fairly common computing core, which allows you to evaluate the prospects for optimizing the application on this platform.

The next part will describe what optimizations have been applied in order to get closer to the expected performance value. The optimization techniques described in this article include, for example:

• scalable parallelization (collaborative thread blocking)
• memory bandwidth increase (cache blocking, register reuse)
• increase in processor performance (vectorization, repartitioning cycles).

In the third part of the article, an algorithm will be described that allows you to automatically select the optimal parameters for launching and building an application. These parameters are usually associated with changes in the source code of the program (for example, loop blocking values), with parameters for the compiler (for example, the cycle sweep factor) and characteristics of the computing system (for example, cache sizes). The resulting algorithm turned out to be faster than traditional heavyweight search techniques. From the simplest implementation to the most optimized, a 6-fold performance improvement was obtained on the Intel Xeon E5-2697v2 processor and approximately 3-fold on the first-generation Intel Xeon Phi coprocessors. In addition to this, the above automatic tuning methodology chooses the optimal launch parameters for any set of input data.


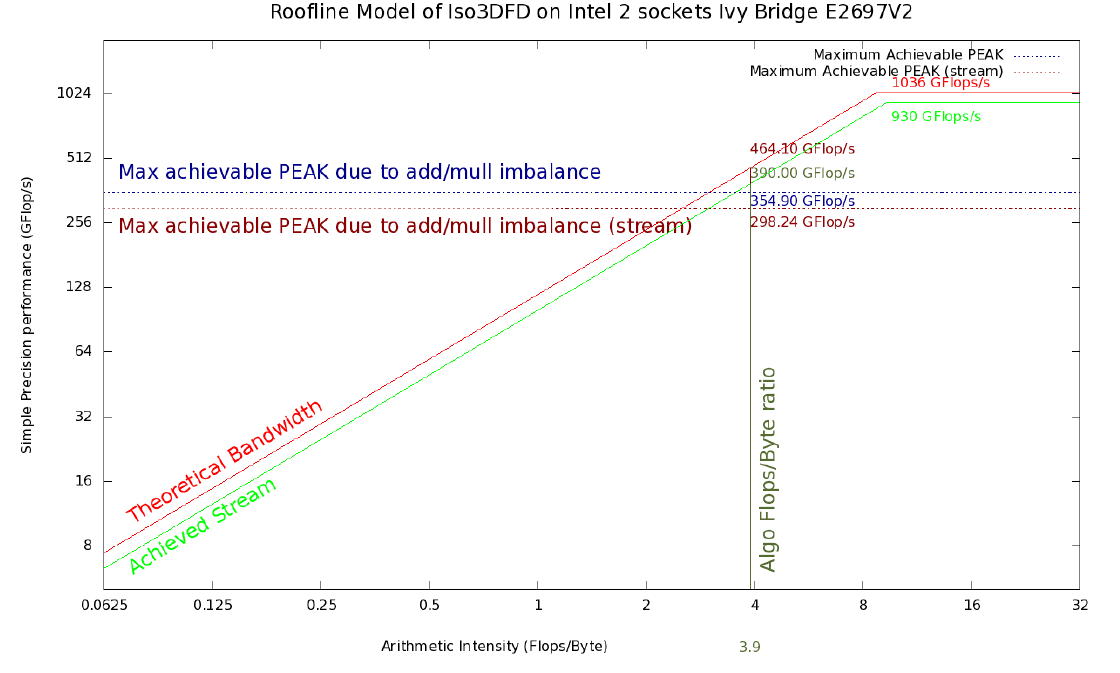
Figure 1. Roofline model Iso3DFD for Ivy Bridge 2S E5-2697 v2. Red and light green lines represent the upper theoretical and achievable limit on the current platform, respectively. The horizontal blue line reflects the maximum achievable memory bandwidths taking into account a certain imbalance between additions and multiplications (#ADD; #MUL) and averaged with the help of Stream triad benchmark (horizontal brown line). The vertical dark green line corresponds to the arithmetic intensity for the core of the Iso3DFD algorithm. Intersections with the remaining lines give the corresponding achievable limits.

Short review

The article describes the characterization (note of the translator - characterization - identification of characteristic features) and the optimization methodology of the 3D finite difference algorithm (3DFD), which is used to solve an acoustic wave equation with a constant or variable density of an isotropic medium (Iso3DFD). Starting with the simplest implementation of 3DFD, we describe a methodology for estimating the best performance that can be obtained for a given algorithm, using its characterization on a specific computing system.
')

Introduction

The finite difference method in the time domain is a widely used technique for modeling waves, for example, for the analysis of wave phenomena and seismic exploration. This method is popular when using seismic analysis techniques such as reverse time migration and full waveform inversion. Varieties of the method include treating the waves as acoustic or elastic, and the propagation medium may be anisotropic, while the density may also vary.

As is known, the choice of a specific numerical scheme for approximation of partial derivatives has a strong influence on the performance of the implementation [1]. In particular, this affects the arithmetic intensity (the number of operations with a floating point per each transmitted machine word) of the 3DFD algorithm. This arithmetic intensity can be further linked to the expected performance using the roofline modeling methodology [2]. This methodology allows us to estimate the level of performance of the implementation with respect to the maximum achievable on a specific computing system. That is, the roofline model sets the framework for productivity growth that can be achieved by optimizing the source code of the program. After the performance of the implementation has reached a certain level, a further increase in productivity can only be obtained by changing the algorithm itself.

For any given computer, its specification defines peak values ​​for the number of floating-point operations (FLOP / s) and for sending data from memory to memory (memory bandwidth). The corresponding maximum achievable performance can be obtained by running standard benchmarks like LINPACK [3] and STREAM triad [4].

The first part of the article will be aimed at assessing the maximum achievable performance of the Iso3DFD algorithm core on a two-socket server and coprocessor. Next, we describe several techniques that can have an important impact on performance. As usual, such optimizations may require some effort and modification of the source code. After that, we will show an auxiliary tool for finding, if not the best, then to some extent the optimal set of parameters for compiling and running the application.


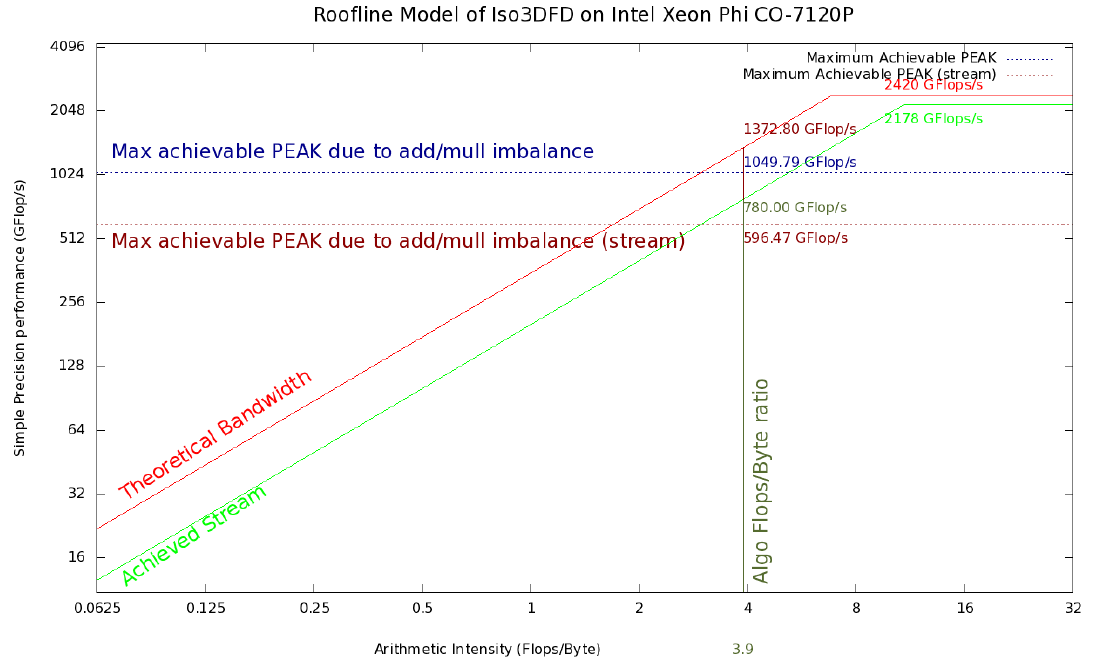
Figure 2. Roofline model Iso3DFD for the Xeon Phi 7120P coprocessor. Red and light green lines represent the upper theoretical and achievable limit on the current platform, respectively. The horizontal blue line reflects the maximum achievable memory bandwidths, taking into account a certain imbalance between additions and multiplications (#ADD; #MUL) and averaged using Stream triad benchmark (horizontal brown line). The vertical dark green line corresponds to the arithmetic intensity for the core of the Iso3DFD algorithm. Intersections with the remaining lines give the corresponding achievable limits.

Performance evaluation

Our core of the Iso3DFD algorithm solves the acoustic isotropic wave equation 16 of the order of discretization in space and 2 of the order of discretization in time. The standard implementation of this 3DFD kernel usually reaches less than 10% of the peak performance of the computing system on floating point operations per second (FLOP / s). We will consider a method for obtaining the roofline model [2] for the Iso3DFD computational core on the CPU and on the Xeon Phi coprocessor. To find the maximum performance of this application, we need to find:

• Peak performance and memory bandwidths (theoretical): 2420 GFLOP / s in single precision and 352 GB / s for Intel Xeon Phi 7120A; 1036 GFLOP / s in single precision and 119 GB / s for 2 Intel Xeon E5-2697v2 processors with 1866 MHz DDR3 memory.
• The values ​​obtained on Linpack (or GEMM) and STREAM triad benchmarks give us the corresponding maximum performance on the platform: 2178 GFLOP / s and 200 GB / s for Intel Xeon Phi 7120A; 930 GFLOP / s and 100 GB / s for 2 Intel Xeon E5-2697v2 processors with 1866 MHz DDR3 memory.
• The arithmetic intensity of the application is calculated based on the number of additions and multiplications (ADD, MUL) of floating-point numbers and the number of bytes sent from memory and a certain number of downloads and records in memory (LOAD, STORE).

The last point follows from the assumption that the computing system has a cache with infinite memory bandwidth and size, and also has zero latency for data access. This defines a kind of flawless memory subsystem, where any array is fully loaded, even if only 1 item is required.

Several other factors may also affect the performance of the entire application using the 3DFD core — the choice of boundary conditions, the IO scheme when addressed in time, and the technology or model of parallel programming. However, in the analysis presented here, we do not consider the boundary conditions and IO. A parallel implementation of the solution to this problem uses the domain decomposition method for distributed systems using the MPI standard along with parallelism on threads on a compute node using OpenMP. In this paper, we consider computations in a subdomain on a single node of a computer system.

Platform arithmetic intensity

Our test system consists of two Xeon E5-2697 CPUs (2S-E5) with 12 cores per CPU, each running at 2.7 GHz without turbo mode. These processors support the AVX extension of a 256-bit wide vector register instruction set. These instructions can perform calculations with 8 single-point floating-point numbers (32 bits) simultaneously (per CPU clock cycle). Thus, the theoretical peak performance can be calculated as 2.7 (GHz) x 8 (SP FP) x 2 (ADD / MULL) x 12 (cores) x 2 (CPUs) = 1036.8 GFLOP / s. Peak bandwidth is calculated using the memory frequency (1866 GHz), the number of memory channels [4], the number of bytes sent per cycle (8), which gives 1866 x 4 x 8 x 2 (CPUs) = 119 GB / s for a dual-processor node 2S-E5. Also, we need to evaluate the achievable values ​​of throughput and performance to characterize the behavior of the application. As a first approximation, let us assume that the performance of any real application can be limited by the memory bandwidth (totally bandwidth bound), which in this paper is estimated using Stream triad or processor speed (totally FLOP / s bound or compute bound or CPU bound), which shows the linpack benchmark. The choice of these two benchmarks is purely hypothetical, but we can argue that if they are far from ideal estimates, then surely they are better suited as an approximation than the peak theoretical values ​​of the computing system.

On the 2S-E5, the Linpack system gives 930 GFLOP / s, and a Stream triad 100 GB / s. Then we can calculate the arithmetic intensity (AI) for theoretical and real maximum indicators, respectively, as:
AI (theoretical, CPU) = 1036.8 / 119 = 8.7 FLOP / byte
AI (achievable, CPU) = 930/100 = 9.3 FLOP / byte

With these values, we can characterize any computational core as follows: if the arithmetic intensity of the core is more (less) than 9.3 FLOP / byte, we can say that this core is limited by the processor speed - CPU bound (memory bandwidth).

Similar calculations for Linpack and Stream triad for Xeon Phi give 2178 GFLOP / s and 200 GB / s, respectively. The theoretical peak ratings are 2420 GFLOP / s and 352 GB / s. Thus, the arithmetic intensity will be equal to:
AI (theoretical, Phi) = 2420.5 / 352 = 6.87 FLOP / byte
AI (achievable, Phi) = 2178/200 = 10.89 FLOP / byte

Arithmetic intensity of the computational core

Roofline model also requires the calculation of the arithmetic intensity of this application. It can be obtained by counting the number of arithmetic operations and memory accesses by visually inspecting the code or using special tools that have access to the counters of the computing system. In the framework of the standard computational kernel of the finite difference scheme [5], we can find 4 downloads (coeff, prev, next, vel), 1 entry (next), 51 addition (calculations of indices are not taken into account) and 27 multiplications (Figure 3).

for(int bz=HALF_LENGTH; bz<n3; bz+=n3_Tblock) for(int by=HALF_LENGTH; by<n2; by+=n2_Tblock) for(int bx=HALF_LENGTH; bx<n1; bx+=n1_Tblock) { int izEnd = MIN(bz+n3_Tblock, n3); int iyEnd = MIN(by+n2_Tblock, n2); int ixEnd = MIN(n1_Tblock, n1-bx); int ix; for(int iz=bz; iz<izEnd; iz++) { for(int iy=by; iy<iyEnd; iy++) { float* next = ptr_next_base + iz*n1n2 + iy*n1 + bx; float* prev = ptr_prev_base + iz*n1n2 + iy*n1 + bx; float* vel = ptr_vel_base + iz*n1n2 + iy*n1 + bx; for(int ix=0; ix<ixEnd; ix++) { float value = 0.0; value += prev[ix]*coeff[0]; for(int ir=1; ir<=HALF_LENGTH; ir++) { value += coeff[ir] * (prev[ix + ir] + prev[ix - ir]) ; value += coeff[ir] * (prev[ix + ir*n1] + prev[ix - ir*n1]); value += coeff[ir] * (prev[ix + ir*n1n2] + prev[ix - ir*n1n2]); } next[ix] = 2.0f* prev[ix] - next[ix] + value*vel[ix]; } }}} 

Figure 3. Computing kernel source code with cache blocking

Arithmetic intensity can be calculated by the formula:

AI = (#ADD + #MUL) / ((#LOAD + #STORE) x word size) (1)

This gives an arithmetic intensity of 3.9 FLOP / byte, which we multiply by the theoretical capacity of each platform to obtain the first estimate of the maximum achievable performance for this algorithm. We get 1372.8 GFLOP / s on Xeon Phi and 461.1 GFLOP / s on 2S-E5. However, the theoretical peak performance value implies the parallel use of two pipelines (one for ADD, the other for MUL), which is impossible in this computational core due to an imbalance between additions and multiplications, thus, this code cannot achieve this estimated maximum value. This means that the achievable maximum value should be averaged using:

(#ADD + #MUL) / (2 x max (add, mul)), (2)

which reflects the ratio of the total possible number of operations for 16 operations with a floating point per cycle (ops / cycle) and the maximum number of additions and multiplications that are performed at 8 ops / cycle, assuming the use of one 256-bit AVX SIMD computing unit. This will give a theoretical estimate of peak performance, taking into account the imbalance of additions and multiplications.
Figures 1 and 2 show a Roofline model with upper bounds of 354.9 GFLOP / s and 1049.8 GFLOP / s for 2S-E5 and Xeon Phi, respectively, obtained using this averaged version of arithmetic intensity.
A more realistic roofline model can be obtained by using the bandwidth of the Stream triad bandwidth by the arithmetic intensity of the computational core (390 GFLOP / s and 780 GFLOP / s, respectively). An even more realistic model can be obtained if we take into account a certain imbalance of additions and multiplications (with the help of (2)), which is indicated by the red dotted line. The new upper bound will be around 298 GFLOP / s for 2S-E5 and 596 GFLOP / s for Xeon Phi. Since our model is based on an impeccable cache model, we assume that the resulting values ​​are still a rough estimate of the maximum achievable performance values. As demonstrated in [2], the resulting roofline can be improved by adding some new entities to the characterization of the computing system, such as the effect and limitations of the cache memory.

To be continued…

Bibliography

1. D. Imbert, K. Immadouedine, P. Thierry, H. Chauris, and L. Borges, “Tips and tricks for finite difference,” in Expanded Abstracts. Soc. Expl. Geophys., 2011, pp. 3174-3178.
2. S. Williams, A. Waterman, and D. Patterson, “Roadmap to Dependable Software, vol. 52, pp. 65–76, April 2009.
3. J. Dongarra, P. Luszczek, and A. Petitet, “The linpack benchmark: past, present and future,” Concurrency and Computation: Practice and Experience, vol. 15, no. 9, pp. 803-820, 2003, doi: 10.1002 / cpe.728.
4. JD McCalpin, “Stream: Sustainable Memory Bandwidth,” University of Virginia, Charlottesville, Virginia, Tech. Rep., 1991-2007, a continually updated technical report. www.cs.virginia.edu/stream
5. L. Borges, “Experiences in imaging code for Intel Xeon Phi coprocessor.”, 2012. software.intel.com/en-us/blogs/2012/10/26/experiences-in-developing-seismic-imaging-code -for-intel-xeon-phi-coprocessor
6. JH Holland, “Genetic algorithms and the optimal allocation of trials,” SIAM Journal of Computing, vol. 2, no. 2, pp. 88–105, 1973.