The book "Eternity. In search of the ultimate theory of time "
Hello! We decided to share the translation of the chapter "Quantum Time" from the book of Sean Carroll:
 What is time in the modern sense and why does it have exactly such properties? Why does time always move in one direction? Why are there irreversible processes? Twenty years ago, Stephen Hawking tried to explain time through the Big Bang theory. Now Sean Carroll, one of the leading theoretical physicists of our time, will introduce you to the delightful paradigm of the theory of the arrow of time, which covers subjects from the entropy of quantum mechanics to time travel in information theory and the meaning of life.
What is time in the modern sense and why does it have exactly such properties? Why does time always move in one direction? Why are there irreversible processes? Twenty years ago, Stephen Hawking tried to explain time through the Big Bang theory. Now Sean Carroll, one of the leading theoretical physicists of our time, will introduce you to the delightful paradigm of the theory of the arrow of time, which covers subjects from the entropy of quantum mechanics to time travel in information theory and the meaning of life.
The book "Eternity. Searching for the ultimate theory of time is not just the next step on the path to understanding why the Universe exists - this is an excellent reading for a wide circle of readers who are interested in the physics and structure of our world.
')
Many of those who have attended the elementary physics course at the university may not agree with the statement that we understand Newtonian mechanics on an intuitive level. The only association that this object causes for them is the crazy merry-go-round of blocks, vectors and inclined planes, and they would never even think of calling it “intuitive”.
However, although the process of performing calculations within the framework of Newtonian mechanics — solving homework or sending astronauts to the moon — can be unbearably complicated, the concepts underlying it are actually quite simple. The world is made of tangible things that we can see and recognize: billiard balls, planets, lifting blocks. These things impact or collide with each other, and under the influence of such effects, the direction and speed of their movement change. If the Laplace demon knew the positions and impulses of all the particles in the Universe, he could absolutely accurately predict the past and the future. We know that this is beyond our capabilities, but it is quite within our power to imagine that we know the positions and impulses of several billiard balls on the table free from friction, and, at least in principle, we can imagine the implementation of appropriate mathematical calculations. After this, the matter remains for extrapolation and courage, and we will be able to embrace the entire Universe.
Physicists who wish to emphasize that this is not just a collection of some laws formulated by Newton call Newtonian mechanics “classical” mechanics. Classical mechanics is a way of thinking about the deep structure of the world. Different types of objects - baseballs, gas molecules, electromagnetic waves - obey different rules, but all these rules are similar in their structure. The essence of the similarity is that any object has a certain kind of “position” and a certain kind of “impulse”, and on the basis of this information it is possible to predict what will happen next.
This structure is repeated in many contexts: Newton's own theory of gravity, the 19th century theory of electricity and magnetism, developed by Maxwell, and Einstein’s general theory of relativity fit into the framework of this pattern. Classical mechanics cannot be called another theory; this is a paradigm, a way of conceptualizing the essence of a physical theory, which demonstrated the amazing scale of success when applied at the empirical level. After the publication of his masterpiece Philosophiæ Naturalis Principia Mathematica ("The Mathematical Principles of Natural Philosophy") by Newton in 1687, it became almost impossible to imagine that you could do something differently in physics. The world is made of bodies characterized by positions and impulses that move under the influence of certain sets of forces; the task of physics was to classify these bodies by type and find out what forces act on them. On this, her work was to be completed.
Nevertheless, we already know that not everything is so simple and classical mechanics is wrong. In the first decades of the 20th century, physicists who tried to understand the behavior of matter on a microscopic scale had to gradually come to terms with the idea that the old rules would have to be declared invalid and replaced with something else. Quantum mechanics has become something else - perhaps the greatest triumph of human reason and imagination in all of history. Quantum mechanics offers a picture of the world that is radically different from the picture created by classical mechanics, and scientists would never seriously think about it if experimental data did not rule out any other options. Today, quantum mechanics is enjoying the status that classical mechanics wore with pride at the dawn of the 20th century: it passed many empirical tests with success, and most researchers agree that the final laws of physics should be quantum-mechanical in nature.
However, despite this triumph, quantum mechanics remains an extremely mysterious subject. Physicists completely trust quantum mechanics in the sense of practical application: they build theories, make predictions and experimentally test theoretical results, without encountering any ambiguities or uncertainties along the way. Nevertheless, we still cannot be completely sure if we know what quantum mechanics really is. There is one solid area of intellectual activity in which many talented scientists and philosophers spend their time and energy. This direction is known as the “interpretation of quantum mechanics”. A century ago, there was no “interpretation of classical mechanics” - classical mechanics is quite simple and understandable, so that its interpretation does not require much effort. But as for quantum mechanics, it is not yet clear to us how to think and talk about it correctly.
This preoccupation with interpretations arises from a single basic difference between quantum mechanics and classical mechanics, which at the same time seems both banal and having truly crushing consequences.
According to quantum mechanics, what we are capable of observing in the outside world is only a tiny subset of what actually exists.
Attempts to explain this principle often only erode it beyond recognition. "It's like that friend of yours with a wonderful smile, who, no matter how you take a picture, your smile disappears somewhere." In fact, quantum mechanics is much more substantial. In the classical world, difficulties may arise in order to accurately measure some quantity; extreme care must be taken not to disturb the system under study. However, nothing in classical physics forbids us to be so careful. In quantum mechanics, on the other hand, there is an insurmountable obstacle, due to which complete and non-destructive observations of the physical system are not available to us. This is simply not generally possible. What exactly happens when you try to observe an object or system, and what can be considered an actual “dimension” - these are the main questions. This riddle has the extremely useful name of “measurement problem” (with the same success, a problem with a car could be called a situation when a car falls off a cliff and, flying several hundred feet, it breaks about rocks into small pieces). In successful physical theories, there should be no such uncertainties; Clear definitions are the main thing that interests us. Quantum mechanics, despite its undoubted success, has not yet reached such a level of clarity.
Nevertheless, this does not mean at all that science has gone astray or that the riddles of quantum mechanics can justify any of their beliefs. In particular, quantum mechanics does not claim that you are able to change reality, just thinking about it, or that modern physics has just rediscovered the wisdom of the ancient Buddhists. The rules exist, and we know how they operate in conditions of interest to our daily lives. However, we would like to understand how these rules work in all situations that you can imagine.
Most modern physicists deal with the problems of interpreting quantum mechanics with the help of the “denial” strategy proven by centuries. They know how rules work in cases of interest to them, they can force quantum mechanics to work in certain circumstances and achieve amazing agreement with experimental data, and they absolutely do not want to bother with annoying questions about what it all means and whether you can call it The theory is absolutely correct. Such a strategy for the most part fully meets our goals in this book. The problem of the arrow of time stood before Boltzmann and his colleagues even before the invention of quantum mechanics, and we can also talk long and productively about entropy and cosmology, without worrying about the details of quantum mechanics.
Yet at some point we will have to look at the problem in the face. In the end, the arrow of time is a fundamental mystery, and it is highly likely that quantum mechanics will play a decisive role in finding the answer to it. However, there is something that is of even greater interest to us: the very process of measurement, which is the focus of all interpretative confusion, has a remarkable property, namely, irreversibility. Alone in the crowd of generally accepted and well-known laws of physics, the process of quantum measurement determines the arrow of time. Once you have done it, you will not be able to cancel your deed. Therein lies the mystery.
Perhaps this mysterious irreversibility is similar in nature to the mysterious thermodynamic irreversibility described by the second principle: it is created by approximations and discarding of information, while the fundamental physical processes themselves are reversible. In this chapter I will defend this point of view. Nevertheless, there is still no consensus among experts on this issue. The only thing that does not cause doubts is the need to seriously deal with the problem of measurement, if we are interested in the arrow of time.
Quantum cat
Thanks to the thought experiments of Erwin Schrödinger, tradition has firmly taken root in the scientific community when discussing quantum mechanics to experiment on cats. Schrödinger's cat was designed to illustrate the difficulties associated with the problem of measurement, but before we delve into the subtleties, we spend some time studying the basics of the theory. And in our mental experiments no animal will suffer.
Imagine that your cat Kitty has two favorite places in the house: on the sofa and under the table in the living room. In the real world, there are infinitely many positions that a physical object like a cat can take; there are certainly infinitely many meanings of its impulse, even if your cat usually moves around the apartment rather slowly. In order to get to the essence of quantum mechanics, we will all greatly simplify. So imagine that we can fully describe the state of Kitty, as is customary in classical mechanics, simply indicating whether it is on the sofa or under the table. We discard all information about its speed, do not take into account exactly which part of the sofa it lies on, and do not take into account any other provisions that do not fall under the definition of "sofa" and "table". From the classical point of view, we simplify Kitty to a two-state system. (Systems with two states exist in the real world; for example, the spin of an electron or photon can be directed either up or down. The quantum state of a two-state system is described by a “qubit” (quantum bit).)
And here we meet with the first major difference between quantum mechanics and classical mechanics: in quantum mechanics there is no such thing as a “cat location”. Classical mechanics assumes that we do not know where Kitty is, so we can make statements like: “I think she is sitting under the table with a probability of 75%.” However, this is only a statement about our ignorance, and not about the state of the world; the fact that the cat is in one of the possible locations is indisputable, and it does not depend on whether we know about it or not.
In quantum mechanics, there are no indisputable facts that testify to the presence of Kitty (or anything else) in a particular place. Simply the space of states in quantum mechanics does not work that way. Instead, a piece known as the wave function is used to indicate states. And the wave function does not give results like: “the cat lies on the sofa” or “the cat lies under the table”. She is able to report only things like: “if we look, then with a probability of 75% we will find a cat under the table, and with a probability of 25% we will find her on the sofa”
The difference between “incomplete knowledge” and “fundamental quantum uncertainty” is worth digging a little longer. If the wave function says that with a 75 percent probability we will find a cat under the table, and with a 25 percent chance on the sofa, does this mean that with a 75% probability the cat is under the table, and with a probability of 25% she is on the sofa ? No, there is no such thing as a “cat is there”. Its quantum state is described by the superposition of two different positions with which we could work in classical mechanics. The point is not even that both statements are true at the same time, but that there is simply no “true” location in which the cat resides. The wave function is the best description of the reality of the cat, which only we are able to build.
It is clear that it is very difficult to agree with such statements, having first encountered them. And if frankly, our world does not seem so at all to us. When we look around, we see cats and planets and even electrons occupying certain positions, and not in the superpositions of various positions described by wave functions. But this is the secret of the magic of quantum mechanics: what we see does not necessarily coincide with reality. The wave function does exist, but we are not able to see it; we see things as if they are in certain ordinary classical configurations.
However, this absolutely does not mean that we cannot rely on classical physics in such matters as playing basketball or launching satellites into orbit. In quantum mechanics, there is no “classical limit” in which objects behave as if Newton was always right, and this limit includes all our everyday experience. We never find objects of macroscopic size, such as cats, in superpositions in the form of "75% here, 25% there"; for them, always "99.9999999 percent (or more) here, 0.0000001 percent (or much less) there." Classical mechanics is a rough description of the work of the macroscopic world, and this is a very good approximation. The real world lives according to the rules of quantum mechanics, but classical mechanics are more than enough for everyday life. Just starting to consider the atoms and elementary particles, we are fully faced with the consequences of quantum mechanics and we understand that now without it anywhere.
How wave functions work
You may be wondering: how do we know that what is written above is true? In the end, what's the difference between "there is a 75 percent chance of seeing a cat under the table" and "there is a 75 percent chance that the cat is under the table." It is difficult to imagine an experiment that could distinguish between these probabilities; after all, the only way to find out where a cat is is to look at its favorite places. However, there is a critical phenomenon by which the essence of the difference becomes apparent. This is quantum interference. To understand what this means, you have to be patient and go deep into the details of how the wave functions actually work.
In classical mechanics, where to describe the state of a particle, its position and momentum are indicated, this state can be thought of as a set of numbers. For one particle in the usual three-dimensional space, it is necessary to specify six numbers: the position in each of the three directions and the momentum in each of the three directions. In quantum mechanics, a state is described by a wave function, which can also be imagined as a set of numbers. The task of these numbers is to inform us for any observation or measurement, which we only want to do, what is the probability that we will get a certain result. Thus, it would seem quite natural to assume that the numbers we need are the most ordinary probabilities: the likelihood that we will see Kitty on the sofa, the likelihood that we will see Kitty under the table, etc.
It turns out, however, that this does not work at all. Wave functions are actually similar to waves: a typical wave function oscillates in space and time like a wave on the surface of a pond. This is not entirely obvious in our simple example, which provides for only two possible results of observations: "on the couch" and "under the table." But if we consider observations with a continuous set of possible outcomes, for example, monitoring the position of a real cat in a real room, then much will immediately become clear. The wave function is similar to a wave on the surface of a pond; the only difference is that it is a wave in space of all possible results of observation: for example, all possible positions in a room.
When we see a real wave, we notice that relative to the surface of the pond in a calm state, the height of the water in the wave in different places is different. Somewhere it is above the level of calm water, and somewhere it falls below. In order to describe the wave mathematically, we could associate with each point of the pond amplitude - the water level relative to the surface of the undisturbed water surface. In some places the amplitude will be positive, in others - negative. Wave functions in quantum mechanics work the same way. With each possible result of observation, the wave function associates a number, which we call amplitude and which can be positive or negative. The total wave function consists of a specific amplitude for each possible observation result; these are the numbers describing the state in quantum mechanics, similar to the positions and impulses that describe the state in classical mechanics. There is an amplitude corresponding to Kitty's stay under the table, and another amplitude corresponding to being on the sofa.
Under such conditions, we have only one unsolved problem: we are talking about probabilities, and the probability of an event occurrence can never be a negative number. Thus, it cannot be argued that the amplitude associated with a particular observation result gives the likelihood of this result occurring; instead, there should be a method for calculating the probability based on the known amplitude value. Fortunately, the calculation is very simple! In order to get the probability, you need to take the amplitude and square it:
(probability of seeing X) = (amplitude associated with X) 2.
Thus, if the Kitty wave function connects an amplitude of 0.5 with the ability to see a cat on the sofa, the probability of actually seeing it there is (0.5) 2 = 0.25, or 25%. It is fundamentally important that the amplitude value could be negative, that is –0.5, and we would still get the same answer: (–0.5) 2 = 0.25. This may seem like a senseless overkill — two different amplitudes correspond to the same physical situation, but it turns out that the presence of positive and negative values plays a key role in the evolution of states in quantum mechanics.
Interference
Now that we know that wave functions can associate negative amplitudes with possible observations, we can return to the question of why we even talk about wave functions and superpositions, instead of simply assigning probabilities to different outcomes. The reason lies in the interference, and these negative values are necessary in order to figure out where it comes from. We can add two (non-zero) amplitudes and get zero, which would be impossible if the amplitudes never took negative values.
In order to understand how this works, let's complicate our feline dynamics model a bit. Imagine that we see Kitty coming out of a bedroom on the second floor. Thanks to our previous observations of her movements around the house, we collected a lot of information about how this quantum cat works. We know that if she descends to the first floor, she will inevitably end up either on the sofa or under the table and nowhere else (that is, her final state is a wave function describing the superposition of staying on the sofa and staying under the table). However, suppose also that we are aware of the existence of two possible paths leading from the bed on the second floor to one of the resting places on the first floor: Kitty will make a stop either at the bowl of food to refresh herself, or at the scraper to sharpen her claws. In the real world, classical mechanics is enough to describe all these possibilities, but in our idealized world of mental experiment, we believe that quantum effects play an important role.
Now let's see what results our observation actually gives. We will conduct an experiment in two different ways. First, after seeing Kitty on the first floor, we will quietly follow her, in order to see what route she follows: past a bowl of food or past a scraper. In fact, it has a wave function that describes the superposition of both possibilities, but when we conduct an actual experiment, we always get a concrete result. We are quieter than water below the grass, and the cat does not notice us at all; if you want, you can even imagine that we equipped the whole house with spy cameras or laser sensors. It doesn’t matter at all what technology we use to find out if Kitty comes to a bowl or a scraper; the main thing is that we have watched this action.
We find that Kitty stops at the bowl exactly in half of the cases and in the same way makes a stop at the scraper in half of the cases (in order to simplify the conditions as much as possible, we assume that she visits either one place or the other, but never both). No observation, of course, by itself reveals a wave function; it only allows us to say that this particular time we saw a cat either at the scraper or at the bowl. But imagine that we repeat this experiment many times, and this gives us the opportunity to make sound conclusions regarding the probabilities of these two events.
However, we do not stop there. We allow Kitty to continue on her way to the sofa, or under the table, and after she gets to rest, we again look at the place she chose. We also repeat this experiment enough times to determine probabilities. Now we find that it is completely unimportant whether it stopped at the scraper or at the bowl of food; in both situations, we see that exactly in half of the cases she eventually comes to the sofa, and in half - under the table, and the choice of the final resting place is completely independent of whether she went to him through a bowl of food or a scraper. Obviously, the intermediate step on this route does not play a special role; Regardless of where the cat stops on the way, the wave function at the end gives equal probabilities for the sofa and for the table.
And now the fun begins. This time we will not watch at all what Kitty takes an intermediate step on her way to the sofa or table; we are not interested in whether it stops at the scratching post or at the bowl of food. We just wait for her to sit on the sofa or under the table, and then check where she is by restoring the resulting probabilities derived from the wave function. What result should be expected?
In a world where classical mechanics reign, we know what we must see. When we spied on the cat, we were very careful that our observation did not affect her actions, and in half the cases we found her on the sofa, and in half - under the table, no matter what route she went. Obviously, even if we do not see what she does along the way, this should not play any role: in any case, in the last step we have two outcomes with equal probabilities. Thus, even without observing the intermediate stage, we should still get the same probability values.
However, this is not the case at all. This is not what we see in our idealized world of mental experiment, where the cat is a real quantum object. When we decide not to look, Kitty stops on the way at the bowl of food or at the scraper, it turns out that in 100% of cases at the end she gets rest on the sofa! We never find it under the table, that is, the final wave function associates a zero amplitude with this possible result. Obviously, if all this is true, then the presence of spy cameras dramatically changed the wave function of the cat. Possible options are listed in the table below.

And this is not at all a thought experiment; such an experience was indeed carried out. Not on real cats, which undoubtedly belong to macroscopic objects and are well described in the classical limit, but on individual photons in the course of an experiment known as the “double-slit experiment”. There are two slits through which a photon can fly, and if we do not observe what gap it flies through, then we get one wave function, and if we observe, it is completely different, no matter how careful and unobtrusive the control was.
This is how it is explained. Imagine that we decided to trace where Kitty stops - at the bowl or at the scratching post, and we see that she stopped at the scratching post. Having completed her business with a scratching post, she evolves into a superposition, where staying on a sofa and staying under the table are equally likely. In particular, due to the characteristics of the initial Kitty state and certain aspects of quantum feline dynamics, the resulting wave function associates equal positive amplitudes with the “sofa” and “table”. Now consider another variant of the intermediate stage, when we see that the cat stops at the bowl with food. In this case, the final wave function connects the negative amplitude with the table, and the positive with the sofa are equal, albeit opposite in sign, values, and, consequently, the corresponding probabilities are absolutely the same.
However, if we do not observe the cat and do not see it at the intermediate stage - at the claw-head or bowl, then (in accordance with the nature of our experiment) at this intermediate step she is in a superposition of two possibilities. : , , , . , - , ; , . , , . . , , ( , ), .
, — «» , - .
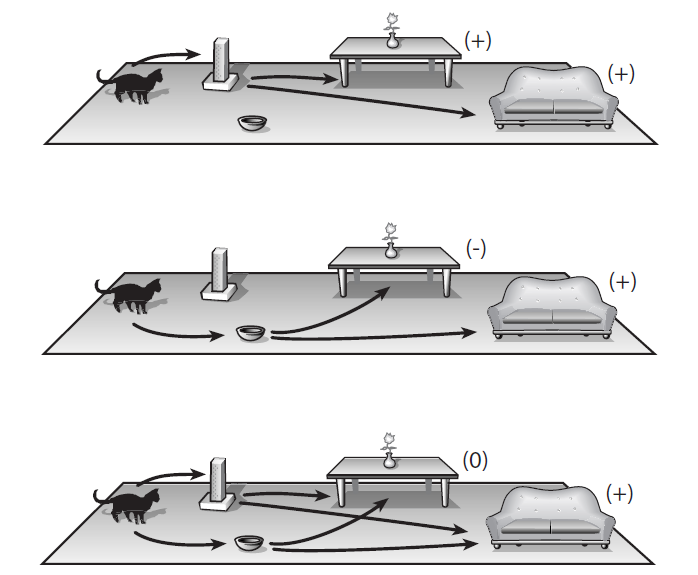
Fig. 11.1. . , -, , — . , , , , ( ). , , . ( )
, , , .
, , . : — ? — . , . , , .
— , , , « ». - , . - , , .
More information about the book can be found on the publisher's website.
Table of contents
Excerpt
25% —
 What is time in the modern sense and why does it have exactly such properties? Why does time always move in one direction? Why are there irreversible processes? Twenty years ago, Stephen Hawking tried to explain time through the Big Bang theory. Now Sean Carroll, one of the leading theoretical physicists of our time, will introduce you to the delightful paradigm of the theory of the arrow of time, which covers subjects from the entropy of quantum mechanics to time travel in information theory and the meaning of life.
What is time in the modern sense and why does it have exactly such properties? Why does time always move in one direction? Why are there irreversible processes? Twenty years ago, Stephen Hawking tried to explain time through the Big Bang theory. Now Sean Carroll, one of the leading theoretical physicists of our time, will introduce you to the delightful paradigm of the theory of the arrow of time, which covers subjects from the entropy of quantum mechanics to time travel in information theory and the meaning of life.The book "Eternity. Searching for the ultimate theory of time is not just the next step on the path to understanding why the Universe exists - this is an excellent reading for a wide circle of readers who are interested in the physics and structure of our world.
')
Quantum time
Many of those who have attended the elementary physics course at the university may not agree with the statement that we understand Newtonian mechanics on an intuitive level. The only association that this object causes for them is the crazy merry-go-round of blocks, vectors and inclined planes, and they would never even think of calling it “intuitive”.
However, although the process of performing calculations within the framework of Newtonian mechanics — solving homework or sending astronauts to the moon — can be unbearably complicated, the concepts underlying it are actually quite simple. The world is made of tangible things that we can see and recognize: billiard balls, planets, lifting blocks. These things impact or collide with each other, and under the influence of such effects, the direction and speed of their movement change. If the Laplace demon knew the positions and impulses of all the particles in the Universe, he could absolutely accurately predict the past and the future. We know that this is beyond our capabilities, but it is quite within our power to imagine that we know the positions and impulses of several billiard balls on the table free from friction, and, at least in principle, we can imagine the implementation of appropriate mathematical calculations. After this, the matter remains for extrapolation and courage, and we will be able to embrace the entire Universe.
Physicists who wish to emphasize that this is not just a collection of some laws formulated by Newton call Newtonian mechanics “classical” mechanics. Classical mechanics is a way of thinking about the deep structure of the world. Different types of objects - baseballs, gas molecules, electromagnetic waves - obey different rules, but all these rules are similar in their structure. The essence of the similarity is that any object has a certain kind of “position” and a certain kind of “impulse”, and on the basis of this information it is possible to predict what will happen next.
This structure is repeated in many contexts: Newton's own theory of gravity, the 19th century theory of electricity and magnetism, developed by Maxwell, and Einstein’s general theory of relativity fit into the framework of this pattern. Classical mechanics cannot be called another theory; this is a paradigm, a way of conceptualizing the essence of a physical theory, which demonstrated the amazing scale of success when applied at the empirical level. After the publication of his masterpiece Philosophiæ Naturalis Principia Mathematica ("The Mathematical Principles of Natural Philosophy") by Newton in 1687, it became almost impossible to imagine that you could do something differently in physics. The world is made of bodies characterized by positions and impulses that move under the influence of certain sets of forces; the task of physics was to classify these bodies by type and find out what forces act on them. On this, her work was to be completed.
Nevertheless, we already know that not everything is so simple and classical mechanics is wrong. In the first decades of the 20th century, physicists who tried to understand the behavior of matter on a microscopic scale had to gradually come to terms with the idea that the old rules would have to be declared invalid and replaced with something else. Quantum mechanics has become something else - perhaps the greatest triumph of human reason and imagination in all of history. Quantum mechanics offers a picture of the world that is radically different from the picture created by classical mechanics, and scientists would never seriously think about it if experimental data did not rule out any other options. Today, quantum mechanics is enjoying the status that classical mechanics wore with pride at the dawn of the 20th century: it passed many empirical tests with success, and most researchers agree that the final laws of physics should be quantum-mechanical in nature.
However, despite this triumph, quantum mechanics remains an extremely mysterious subject. Physicists completely trust quantum mechanics in the sense of practical application: they build theories, make predictions and experimentally test theoretical results, without encountering any ambiguities or uncertainties along the way. Nevertheless, we still cannot be completely sure if we know what quantum mechanics really is. There is one solid area of intellectual activity in which many talented scientists and philosophers spend their time and energy. This direction is known as the “interpretation of quantum mechanics”. A century ago, there was no “interpretation of classical mechanics” - classical mechanics is quite simple and understandable, so that its interpretation does not require much effort. But as for quantum mechanics, it is not yet clear to us how to think and talk about it correctly.
This preoccupation with interpretations arises from a single basic difference between quantum mechanics and classical mechanics, which at the same time seems both banal and having truly crushing consequences.
According to quantum mechanics, what we are capable of observing in the outside world is only a tiny subset of what actually exists.
Attempts to explain this principle often only erode it beyond recognition. "It's like that friend of yours with a wonderful smile, who, no matter how you take a picture, your smile disappears somewhere." In fact, quantum mechanics is much more substantial. In the classical world, difficulties may arise in order to accurately measure some quantity; extreme care must be taken not to disturb the system under study. However, nothing in classical physics forbids us to be so careful. In quantum mechanics, on the other hand, there is an insurmountable obstacle, due to which complete and non-destructive observations of the physical system are not available to us. This is simply not generally possible. What exactly happens when you try to observe an object or system, and what can be considered an actual “dimension” - these are the main questions. This riddle has the extremely useful name of “measurement problem” (with the same success, a problem with a car could be called a situation when a car falls off a cliff and, flying several hundred feet, it breaks about rocks into small pieces). In successful physical theories, there should be no such uncertainties; Clear definitions are the main thing that interests us. Quantum mechanics, despite its undoubted success, has not yet reached such a level of clarity.
Nevertheless, this does not mean at all that science has gone astray or that the riddles of quantum mechanics can justify any of their beliefs. In particular, quantum mechanics does not claim that you are able to change reality, just thinking about it, or that modern physics has just rediscovered the wisdom of the ancient Buddhists. The rules exist, and we know how they operate in conditions of interest to our daily lives. However, we would like to understand how these rules work in all situations that you can imagine.
Most modern physicists deal with the problems of interpreting quantum mechanics with the help of the “denial” strategy proven by centuries. They know how rules work in cases of interest to them, they can force quantum mechanics to work in certain circumstances and achieve amazing agreement with experimental data, and they absolutely do not want to bother with annoying questions about what it all means and whether you can call it The theory is absolutely correct. Such a strategy for the most part fully meets our goals in this book. The problem of the arrow of time stood before Boltzmann and his colleagues even before the invention of quantum mechanics, and we can also talk long and productively about entropy and cosmology, without worrying about the details of quantum mechanics.
Yet at some point we will have to look at the problem in the face. In the end, the arrow of time is a fundamental mystery, and it is highly likely that quantum mechanics will play a decisive role in finding the answer to it. However, there is something that is of even greater interest to us: the very process of measurement, which is the focus of all interpretative confusion, has a remarkable property, namely, irreversibility. Alone in the crowd of generally accepted and well-known laws of physics, the process of quantum measurement determines the arrow of time. Once you have done it, you will not be able to cancel your deed. Therein lies the mystery.
Perhaps this mysterious irreversibility is similar in nature to the mysterious thermodynamic irreversibility described by the second principle: it is created by approximations and discarding of information, while the fundamental physical processes themselves are reversible. In this chapter I will defend this point of view. Nevertheless, there is still no consensus among experts on this issue. The only thing that does not cause doubts is the need to seriously deal with the problem of measurement, if we are interested in the arrow of time.
Quantum time
Quantum cat
Thanks to the thought experiments of Erwin Schrödinger, tradition has firmly taken root in the scientific community when discussing quantum mechanics to experiment on cats. Schrödinger's cat was designed to illustrate the difficulties associated with the problem of measurement, but before we delve into the subtleties, we spend some time studying the basics of the theory. And in our mental experiments no animal will suffer.
Imagine that your cat Kitty has two favorite places in the house: on the sofa and under the table in the living room. In the real world, there are infinitely many positions that a physical object like a cat can take; there are certainly infinitely many meanings of its impulse, even if your cat usually moves around the apartment rather slowly. In order to get to the essence of quantum mechanics, we will all greatly simplify. So imagine that we can fully describe the state of Kitty, as is customary in classical mechanics, simply indicating whether it is on the sofa or under the table. We discard all information about its speed, do not take into account exactly which part of the sofa it lies on, and do not take into account any other provisions that do not fall under the definition of "sofa" and "table". From the classical point of view, we simplify Kitty to a two-state system. (Systems with two states exist in the real world; for example, the spin of an electron or photon can be directed either up or down. The quantum state of a two-state system is described by a “qubit” (quantum bit).)
And here we meet with the first major difference between quantum mechanics and classical mechanics: in quantum mechanics there is no such thing as a “cat location”. Classical mechanics assumes that we do not know where Kitty is, so we can make statements like: “I think she is sitting under the table with a probability of 75%.” However, this is only a statement about our ignorance, and not about the state of the world; the fact that the cat is in one of the possible locations is indisputable, and it does not depend on whether we know about it or not.
In quantum mechanics, there are no indisputable facts that testify to the presence of Kitty (or anything else) in a particular place. Simply the space of states in quantum mechanics does not work that way. Instead, a piece known as the wave function is used to indicate states. And the wave function does not give results like: “the cat lies on the sofa” or “the cat lies under the table”. She is able to report only things like: “if we look, then with a probability of 75% we will find a cat under the table, and with a probability of 25% we will find her on the sofa”
The difference between “incomplete knowledge” and “fundamental quantum uncertainty” is worth digging a little longer. If the wave function says that with a 75 percent probability we will find a cat under the table, and with a 25 percent chance on the sofa, does this mean that with a 75% probability the cat is under the table, and with a probability of 25% she is on the sofa ? No, there is no such thing as a “cat is there”. Its quantum state is described by the superposition of two different positions with which we could work in classical mechanics. The point is not even that both statements are true at the same time, but that there is simply no “true” location in which the cat resides. The wave function is the best description of the reality of the cat, which only we are able to build.
It is clear that it is very difficult to agree with such statements, having first encountered them. And if frankly, our world does not seem so at all to us. When we look around, we see cats and planets and even electrons occupying certain positions, and not in the superpositions of various positions described by wave functions. But this is the secret of the magic of quantum mechanics: what we see does not necessarily coincide with reality. The wave function does exist, but we are not able to see it; we see things as if they are in certain ordinary classical configurations.
However, this absolutely does not mean that we cannot rely on classical physics in such matters as playing basketball or launching satellites into orbit. In quantum mechanics, there is no “classical limit” in which objects behave as if Newton was always right, and this limit includes all our everyday experience. We never find objects of macroscopic size, such as cats, in superpositions in the form of "75% here, 25% there"; for them, always "99.9999999 percent (or more) here, 0.0000001 percent (or much less) there." Classical mechanics is a rough description of the work of the macroscopic world, and this is a very good approximation. The real world lives according to the rules of quantum mechanics, but classical mechanics are more than enough for everyday life. Just starting to consider the atoms and elementary particles, we are fully faced with the consequences of quantum mechanics and we understand that now without it anywhere.
How wave functions work
You may be wondering: how do we know that what is written above is true? In the end, what's the difference between "there is a 75 percent chance of seeing a cat under the table" and "there is a 75 percent chance that the cat is under the table." It is difficult to imagine an experiment that could distinguish between these probabilities; after all, the only way to find out where a cat is is to look at its favorite places. However, there is a critical phenomenon by which the essence of the difference becomes apparent. This is quantum interference. To understand what this means, you have to be patient and go deep into the details of how the wave functions actually work.
In classical mechanics, where to describe the state of a particle, its position and momentum are indicated, this state can be thought of as a set of numbers. For one particle in the usual three-dimensional space, it is necessary to specify six numbers: the position in each of the three directions and the momentum in each of the three directions. In quantum mechanics, a state is described by a wave function, which can also be imagined as a set of numbers. The task of these numbers is to inform us for any observation or measurement, which we only want to do, what is the probability that we will get a certain result. Thus, it would seem quite natural to assume that the numbers we need are the most ordinary probabilities: the likelihood that we will see Kitty on the sofa, the likelihood that we will see Kitty under the table, etc.
It turns out, however, that this does not work at all. Wave functions are actually similar to waves: a typical wave function oscillates in space and time like a wave on the surface of a pond. This is not entirely obvious in our simple example, which provides for only two possible results of observations: "on the couch" and "under the table." But if we consider observations with a continuous set of possible outcomes, for example, monitoring the position of a real cat in a real room, then much will immediately become clear. The wave function is similar to a wave on the surface of a pond; the only difference is that it is a wave in space of all possible results of observation: for example, all possible positions in a room.
When we see a real wave, we notice that relative to the surface of the pond in a calm state, the height of the water in the wave in different places is different. Somewhere it is above the level of calm water, and somewhere it falls below. In order to describe the wave mathematically, we could associate with each point of the pond amplitude - the water level relative to the surface of the undisturbed water surface. In some places the amplitude will be positive, in others - negative. Wave functions in quantum mechanics work the same way. With each possible result of observation, the wave function associates a number, which we call amplitude and which can be positive or negative. The total wave function consists of a specific amplitude for each possible observation result; these are the numbers describing the state in quantum mechanics, similar to the positions and impulses that describe the state in classical mechanics. There is an amplitude corresponding to Kitty's stay under the table, and another amplitude corresponding to being on the sofa.
Under such conditions, we have only one unsolved problem: we are talking about probabilities, and the probability of an event occurrence can never be a negative number. Thus, it cannot be argued that the amplitude associated with a particular observation result gives the likelihood of this result occurring; instead, there should be a method for calculating the probability based on the known amplitude value. Fortunately, the calculation is very simple! In order to get the probability, you need to take the amplitude and square it:
(probability of seeing X) = (amplitude associated with X) 2.
Thus, if the Kitty wave function connects an amplitude of 0.5 with the ability to see a cat on the sofa, the probability of actually seeing it there is (0.5) 2 = 0.25, or 25%. It is fundamentally important that the amplitude value could be negative, that is –0.5, and we would still get the same answer: (–0.5) 2 = 0.25. This may seem like a senseless overkill — two different amplitudes correspond to the same physical situation, but it turns out that the presence of positive and negative values plays a key role in the evolution of states in quantum mechanics.
Interference
Now that we know that wave functions can associate negative amplitudes with possible observations, we can return to the question of why we even talk about wave functions and superpositions, instead of simply assigning probabilities to different outcomes. The reason lies in the interference, and these negative values are necessary in order to figure out where it comes from. We can add two (non-zero) amplitudes and get zero, which would be impossible if the amplitudes never took negative values.
In order to understand how this works, let's complicate our feline dynamics model a bit. Imagine that we see Kitty coming out of a bedroom on the second floor. Thanks to our previous observations of her movements around the house, we collected a lot of information about how this quantum cat works. We know that if she descends to the first floor, she will inevitably end up either on the sofa or under the table and nowhere else (that is, her final state is a wave function describing the superposition of staying on the sofa and staying under the table). However, suppose also that we are aware of the existence of two possible paths leading from the bed on the second floor to one of the resting places on the first floor: Kitty will make a stop either at the bowl of food to refresh herself, or at the scraper to sharpen her claws. In the real world, classical mechanics is enough to describe all these possibilities, but in our idealized world of mental experiment, we believe that quantum effects play an important role.
Now let's see what results our observation actually gives. We will conduct an experiment in two different ways. First, after seeing Kitty on the first floor, we will quietly follow her, in order to see what route she follows: past a bowl of food or past a scraper. In fact, it has a wave function that describes the superposition of both possibilities, but when we conduct an actual experiment, we always get a concrete result. We are quieter than water below the grass, and the cat does not notice us at all; if you want, you can even imagine that we equipped the whole house with spy cameras or laser sensors. It doesn’t matter at all what technology we use to find out if Kitty comes to a bowl or a scraper; the main thing is that we have watched this action.
We find that Kitty stops at the bowl exactly in half of the cases and in the same way makes a stop at the scraper in half of the cases (in order to simplify the conditions as much as possible, we assume that she visits either one place or the other, but never both). No observation, of course, by itself reveals a wave function; it only allows us to say that this particular time we saw a cat either at the scraper or at the bowl. But imagine that we repeat this experiment many times, and this gives us the opportunity to make sound conclusions regarding the probabilities of these two events.
However, we do not stop there. We allow Kitty to continue on her way to the sofa, or under the table, and after she gets to rest, we again look at the place she chose. We also repeat this experiment enough times to determine probabilities. Now we find that it is completely unimportant whether it stopped at the scraper or at the bowl of food; in both situations, we see that exactly in half of the cases she eventually comes to the sofa, and in half - under the table, and the choice of the final resting place is completely independent of whether she went to him through a bowl of food or a scraper. Obviously, the intermediate step on this route does not play a special role; Regardless of where the cat stops on the way, the wave function at the end gives equal probabilities for the sofa and for the table.
And now the fun begins. This time we will not watch at all what Kitty takes an intermediate step on her way to the sofa or table; we are not interested in whether it stops at the scratching post or at the bowl of food. We just wait for her to sit on the sofa or under the table, and then check where she is by restoring the resulting probabilities derived from the wave function. What result should be expected?
In a world where classical mechanics reign, we know what we must see. When we spied on the cat, we were very careful that our observation did not affect her actions, and in half the cases we found her on the sofa, and in half - under the table, no matter what route she went. Obviously, even if we do not see what she does along the way, this should not play any role: in any case, in the last step we have two outcomes with equal probabilities. Thus, even without observing the intermediate stage, we should still get the same probability values.
However, this is not the case at all. This is not what we see in our idealized world of mental experiment, where the cat is a real quantum object. When we decide not to look, Kitty stops on the way at the bowl of food or at the scraper, it turns out that in 100% of cases at the end she gets rest on the sofa! We never find it under the table, that is, the final wave function associates a zero amplitude with this possible result. Obviously, if all this is true, then the presence of spy cameras dramatically changed the wave function of the cat. Possible options are listed in the table below.
And this is not at all a thought experiment; such an experience was indeed carried out. Not on real cats, which undoubtedly belong to macroscopic objects and are well described in the classical limit, but on individual photons in the course of an experiment known as the “double-slit experiment”. There are two slits through which a photon can fly, and if we do not observe what gap it flies through, then we get one wave function, and if we observe, it is completely different, no matter how careful and unobtrusive the control was.
This is how it is explained. Imagine that we decided to trace where Kitty stops - at the bowl or at the scratching post, and we see that she stopped at the scratching post. Having completed her business with a scratching post, she evolves into a superposition, where staying on a sofa and staying under the table are equally likely. In particular, due to the characteristics of the initial Kitty state and certain aspects of quantum feline dynamics, the resulting wave function associates equal positive amplitudes with the “sofa” and “table”. Now consider another variant of the intermediate stage, when we see that the cat stops at the bowl with food. In this case, the final wave function connects the negative amplitude with the table, and the positive with the sofa are equal, albeit opposite in sign, values, and, consequently, the corresponding probabilities are absolutely the same.
However, if we do not observe the cat and do not see it at the intermediate stage - at the claw-head or bowl, then (in accordance with the nature of our experiment) at this intermediate step she is in a superposition of two possibilities. : , , , . , - , ; , . , , . . , , ( , ), .
, — «» , - .
Fig. 11.1. . , -, , — . , , , , ( ). , , . ( )
, , , .
, , . : — ? — . , . , , .
— , , , « ». - , . - , , .
More information about the book can be found on the publisher's website.
Table of contents
Excerpt
25% —
Source: https://habr.com/ru/post/277389/
All Articles