Introduction

I am a software math. I made the biggest leap in my career when I learned to say: “I don’t understand anything!” Now I’m not ashamed to tell the science lord that I am giving a lecture, that I don’t understand what it is, the light, it tells me. And it is very difficult. Yes, it is difficult and embarrassing to admit ignorance. Who would like to admit that he does not know the basics of something there. By virtue of my profession, I have to attend a large number of presentations and lectures, where, I confess, in most cases I want to sleep, because I don’t understand anything. But I don’t understand it because the huge problem of the current situation in science lies in mathematics. She assumes that all students are familiar with absolutely all areas of mathematics (which is absurd). To admit that you do not know what a derivative is (that it is a little later) is embarrassing.

But I learned to say that I do not know what multiplication is. Yes, I do not know what a subalgebra over a Lie algebra is. Yes, I do not know why quadratic equations are necessary in life. By the way, if you are sure that you know, then we have something to talk about! Math is a series of magic tricks. Mathematicians try to confuse and intimidate the public; where there is no confusion, no reputation, no authority. Yes, it is prestigious to speak in as abstract a language as possible, which is complete nonsense.

Do you know what a derivative is? Most likely you will tell me about the limit of the differential relation. In the first year of St. Petersburg State University mathemeh, Viktor Petrovich Havin defined the derivative as the coefficient of the first member of the Taylor series of function at a point (it was a separate gymnastics to determine the Taylor series without derivatives). I laughed at this definition for a long time, until I finally understood what it was about. The derivative is nothing but a measure of how much the function that we differentiate is similar to the function y = x, y = x ^ 2, y = x ^ 3.
')
I now have the honor to lecture students who are afraid of mathematics. If you are afraid of mathematics - we are with you along the way. As soon as you try to read some text, and it seems to you that it is excessively complicated, then know that it is badly written. I affirm that there is not a single area of ​​mathematics that cannot be talked about on the fingers without losing accuracy.

The task for the near future: I instructed my students to understand what a linear-quadratic regulator is . Do not hesitate, spend three minutes of your life, follow the link. If you do not understand, then we are with you along the way. I (a professional mathematician and programmer) did not understand anything either. And I assure you that you can figure it out "on the fingers." At the moment I do not know what it is, but I assure that we will be able to figure it out.

So, the first lecture that I am going to read to my students after they come to me in horror with the words that a linear-quadratic regulator is a terrible baddy that you can never master in your life, these are least squares methods . Can you solve linear equations? If you are reading this text, then most likely not.

So, two points are given (x0, y0), (x1, y1), for example, (1,1) and (3,2), the task is to find the equation of a line passing through these two points:



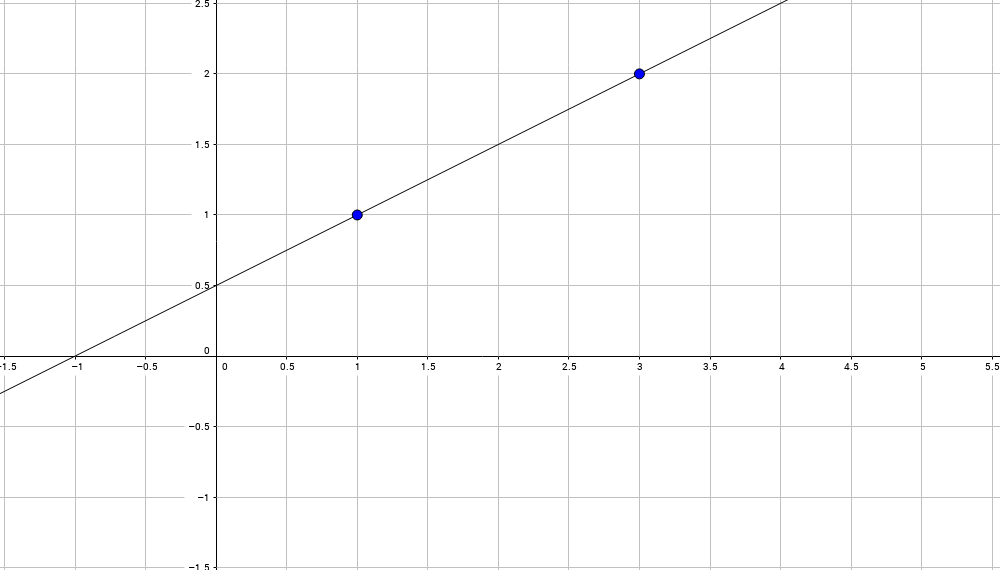
This line should have an equation like the following:



Here alpha and beta are unknown to us, but two points of this straight line are known:



You can write this equation in matrix form:



A lyrical digression should be made here: what is a matrix? The matrix is ​​nothing but a two-dimensional array. This is a way of storing data; you should not give it any more value. It depends on us exactly how to interpret a certain matrix. Periodically, I will interpret it as a linear mapping, periodically as a quadratic form, and sometimes even simply as a set of vectors. This will all be clarified in context.

Let's replace specific matrices with their symbolic representation:



Then (alpha, beta) can be easily found:



More specifically for our previous data:





Which leads to the following equation of a straight line passing through the points (1,1) and (3,2):



Okay, everything is clear. And let's find the equation of a line passing through three points: (x0, y0), (x1, y1) and (x2, y2):



Oh, oh, oh, and yet we have three equations for two unknowns! A standard mathematician will say that there is no solution. And what will the programmer say? And he will first rewrite the previous system of equations in the following form:



And then she will try to find a solution that deviates the least from the given equalities. Let's call the vector (x0, x1, x2) the vector i, (1,1,1) the vector j, and (y0, y1, y2) the vector b:



In our case, the vectors i, j, b are three-dimensional, therefore, (in general) the solution of this system does not exist. Any vector (alpha \ * i + beta \ * j) lies in the plane spanned by the vectors (i, j). If b does not belong to this plane, then there is no solution (equality cannot be achieved in the equation). What to do? Let's look for a compromise. Let's denote by e (alpha, beta) how exactly we have not achieved equality:



And we will try to minimize this error:





Obviously, the error is minimized when the vector e is orthogonal to the plane spanned by the vectors i and j .



In other words: we are looking for such a straight line that the sum of the squares of the lengths of distances from all points to this straight line is minimal:

UPDATE: here I cant, the distance to the line should be measured vertically, and not by the orthogonal projection. This commentator is right.


In other words (carefully, poorly formalized, but on the fingers it should be clear): we take all possible straight lines between all pairs of points and look for the middle straight line between all:



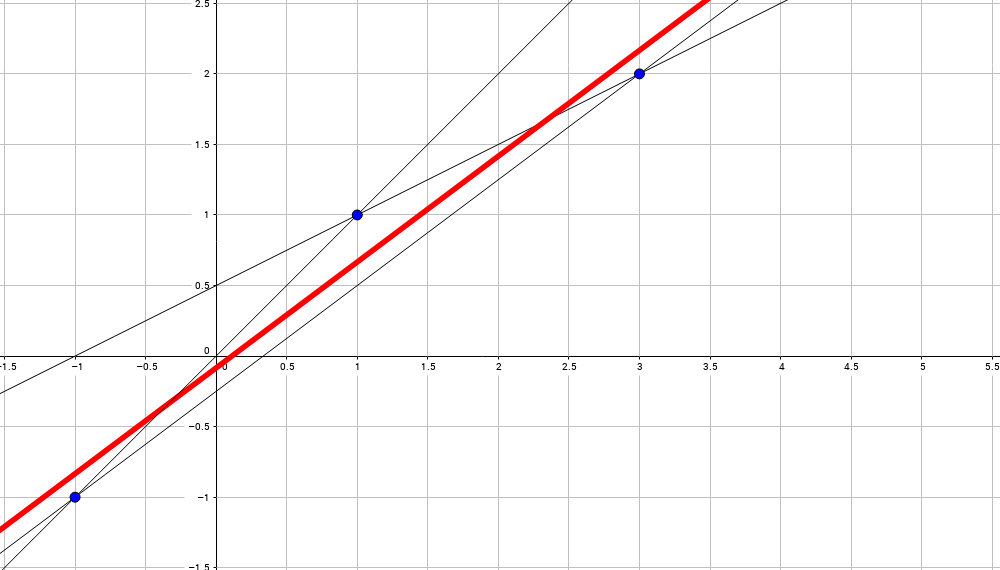
There is another explanation on the fingers: we attach a spring between all data points (here we have three) and a straight line, what we are looking for, and the straight line of the equilibrium state is exactly what we are looking for.

Minimum of quadratic form

So, having this vector b and a plane spanned by the column-vectors of the matrix A (in this case (x0, x1, x2) and (1,1,1)), we are looking for the vector e with a minimum of square length. Obviously, the minimum is attainable only for the vector e , orthogonal to the plane, stretched on the columns-vectors of the matrix A :



In other words, we are looking for a vector x = (alpha, beta) such that:



I remind you that this vector x = (alpha, beta) is the minimum of the quadratic function || e (alpha, beta) || ^ 2:


It would be useful to recall that the matrix can be interpreted, including the quadratic form, for example, the unit matrix ((1,0), (0,1)) can be interpreted as a function x ^ 2 + y ^ 2:





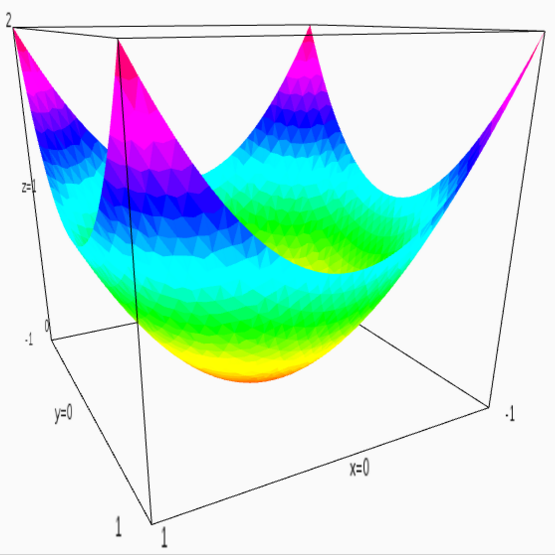
All this gymnastics is known as linear regression .

Laplace equation with Dirichlet boundary condition

Now the simplest real problem: there is a certain triangulated surface, it is necessary to smooth it. For example, let's load a model of my face:



The original commit is available here . To minimize external dependencies, I took the code of my software renderer, already described in detail in the Habré. To solve a linear system, I use OpenNL , this is a great solver, which, however, is very difficult to install: you need to copy two files (.h + .c) to the folder with your project. All anti-aliasing is done with the following code:

    for (int d=0; d<3; d++) {
        nlNewContext();
        nlSolverParameteri(NL_NB_VARIABLES, verts.size());
        nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
        nlBegin(NL_SYSTEM);
        nlBegin(NL_MATRIX);

        for (int i=0; i<(int)verts.size(); i++) {
            nlBegin(NL_ROW);
            nlCoefficient(i, 1);
            nlRightHandSide(verts[i][d]);
            nlEnd(NL_ROW);
        }

        for (unsigned int i=0; i<faces.size(); i++) {
            std::vector<int> &face = faces[i];
            for (int j=0; j<3; j++) {
                nlBegin(NL_ROW);
                nlCoefficient(face[ j     ],  1);
                nlCoefficient(face[(j+1)%3], -1);
                nlEnd(NL_ROW);
            }
        }

        nlEnd(NL_MATRIX);
        nlEnd(NL_SYSTEM);
        nlSolve();

        for (int i=0; i<(int)verts.size(); i++) {
            verts[i][d] = nlGetVariable(i);
        }
    }

X, Y Z , . , , . n A , n b . , — .

A (faces.size()*3 = ) 1 -1, b . , : .

: , , .

:



, , . - :

        for (int i=0; i<(int)verts.size(); i++) {
            float scale = border[i] ? 1000 : 1;
            nlBegin(NL_ROW);
            nlCoefficient(i, scale);
            nlRightHandSide(scale*verts[i][d]);
            nlEnd(NL_ROW);
        }

A , , v_i = verts[i][d], 1000*v_i = 1000*verts[i][d]. ? . , , 1000*1000 . , , . :



:

                nlCoefficient(face[ j     ],  2);
                nlCoefficient(face[(j+1)%3], -2);

, :



:



? , . , , - — . , . , . ? - .

.

, :



, .

:



:


, , , , :

    for (int i=0; i<w*h; i++) {
        if (m.get(i%w, i/w)[0]<128) continue;
        nlBegin(NL_ROW);
        nlCoefficient(i, 1);
        nlRightHandSide(a.get(i%w, i/w)[0]);
        nlScaleRow(100);
        nlEnd(NL_ROW);
    }

    for (int i=0; i<w-1; i++) {
        for (int j=0; j<h-1; j++) {
            for (int d=0; d<2; d++) {
                nlBegin(NL_ROW);
                int v1 = b.get(i,   j    )[0];
                int v2 = b.get(i+d, j+1-d)[0];
                nlCoefficient( i   + j     *w,  1);
                nlCoefficient((i+d)+(j+1-d)*w, -1);
                nlRightHandSide(v1-v2);
                nlScaleRow(10);
                nlEnd(NL_ROW);
            }
        }
    }

:



.

, .. - , , . :

:



. () :



, - , :



, :



, :



:



, :



, , , - . - . :



, . , , .