Carefully about counting single bits
I would like to give the Habr community an article in which I try to give a fairly complete description of the approaches to the algorithms for calculating single bits in variables ranging in size from 8 to 64 bits. These algorithms belong to the section of the so-called “bit magic” or “bit alchemy”, which fascinates with its beauty and non-obviousness many programmers. I want to show that there is nothing difficult in the basics of this alchemy, and you can even develop your own methods of calculating single bits, having become acquainted with the fundamental techniques that make up these algorithms.
Before we begin, I just want to warn you that this article is not for beginners in programming. I need the reader to have a general idea of the simplest bit operations (bitwise "and", "or", shift), to have a good hexadecimal numbering system and to use the imagination quite confidently, presenting in it not always short bit sequences. If possible, everything will be accompanied by pictures, but you know, they only simplify, but do not replace the full presentation.
')
All described techniques were implemented in C language and tested in two modes: 32 and 64 bits. Thus, for a more complete understanding of the article, it would be better that you at least approximately understand the C language. Testing took place on the processor Core 2 Duo E8400 @ 3GHz on 64-bit Windows 7. Measurement of the net operating time of the programs was carried out using the runexe utility. All source codes of the described algorithms are available in the archive on the Yandex disk, their compilation is checked for compilers Visual C ++, Intel C ++, GCC and CLang, so in principle, you should have no problems if someone wants to double-check the results with them. Linux users, I think, know better than me how to test the program runtime on their system, so I don’t give them any advice.
Among the readers, there may be people who find it easier to watch the same thing on the video. I recorded such a video (58 minutes), in which the presentation format is exactly the same, which will be lower in the text, but maybe in a slightly different style, more dry and strictly, while I tried to revive the text a little. Therefore, study the material as it is more convenient to whom.
Now the algorithms generated by one or another set of alchemical methods will be sequentially described, in each section there will be a table comparing the working time for variables of different sizes, and at the end there will be a summary table for all algorithms. All algorithms use pseudonyms for unsigned numbers from 8 to 64 bits.
It is obvious that bit alchemy is not used to shine at the interview, but with the aim of significantly accelerating the programs. Acceleration in relation to what? In relation to the trivial techniques that can come to mind when there is no time to go into the task in more detail. This is the naive approach to calculating bits: we simply “bite off” one bit after another and add them up by repeating the procedure until the number is zero.
I do not see any reason to comment on this trivial cycle. With the naked eye it is clear that if the high bit of the number n is 1, then the cycle will have to go through all the bits of the number before it reaches the high bit.
Changing the type of the input parameter u8 to u16, u32 and u64 we get 4 different functions. Let's test each of them on a stream of 2 32 numbers given in a chaotic order. It is clear that for u8 we have 256 different input data, but for consistency we still run 2 32 random numbers for all these and all subsequent functions, always in the same order (for details you can refer to the curriculum code from the archive ).
The time in the table below is in seconds. For testing, the program was run three times and the average time was selected. The error hardly exceeds 0.1 seconds. The first column reflects the compiler mode (32-bit source code or 64-bit), then 4 columns are responsible for 4 variants of input data.
As we see, the speed of work quite naturally increases with increasing size of the input parameter. The variant when the numbers are 64 bits in size and the calculation is in x86 mode is a little out of general regularity. It's clear that the processor is forced to do fourfold work by doubling the input parameter, and it’s even good that it only copes three times slower.
The first benefit of this approach is that when it is implemented it is difficult to make a mistake, therefore, a program written in this way can become a reference for testing more complex algorithms (this was exactly what was done in my case). The second benefit is versatility and relatively simple portability for numbers of any size.
This alchemical method is based on the idea of zeroing the low-order single bit. Having the number n, we can cast the spell n = n & (n-1), taking the younger one from the number n. The picture below for n = 232 will clarify the situation for people who first learned about this trick.
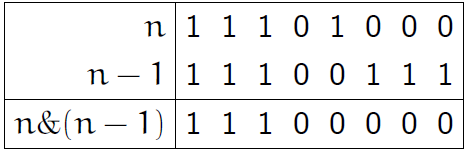
The program code has not changed much.
Now the cycle will be executed exactly as many times as the units in the number n. This does not eliminate the worst case when all the bits in a single number, but significantly reduces the average number of iterations. Will this approach greatly ease the processor's pain? In fact, not much, but for 8 bits it will be even worse. Let me remind you that the summary table of results will be at the end, and here in each section will be its own table.
Let's not rush to move to the "hard" spells, consider the last simple technique that can save even the most inexperienced magician. This solution is not directly related to bit alchemy, but for the sake of completeness, it should be considered without fail. Let's get two tables for 256 and 65536 values, in which the answers for all possible 1-byte and 2-byte values are calculated in advance, respectively.
Now the program for 1 byte will look like this
To calculate the number of bits in larger numbers, they need to be divided into bytes. For example, for u32 there could be such code:
Or such, if we use the table of predalagment for 2 bytes:
Well, then you guessed it, for each option of the size of the input parameter n (except 8 bits) there can be two versions of the pre-calculation, depending on which of the two tables we use. I think the reader understands why we cannot just take and start the BitsSetTableFFFFFFFF table, but there may well be problems where this will be justified.
Does the pre-submission work fast? It all depends on the size, see the table below. The first is for a single byte precondition, and the second is for two byte.
An interesting point: for the x64 mode, the pre-account for u64 works much faster, perhaps it is optimization features, although this does not appear in the second case.
Important note: this algorithm using the pre-calculation is beneficial only if the following two conditions are met: (1) you have extra memory, (2) you need to perform the calculation of the number of single bits much more than the size of the table itself, that is, you can “Play” the time spent on pre-filling the table with some of the simple algorithms. Perhaps you can also keep in mind the exotic condition, which in practice is always fulfilled. You must ensure that the memory access itself is fast and does not slow down other functions of the system. The fact is that accessing the table can throw out from the cache what was originally there and thus slow down some other part of the code. You can hardly find a jamb quickly, but such monstrous optimizations are hardly necessary for anyone to practice in the implementation of ordinary programs.
Finally, take the stronger potions from our alchemy shelf. With the help of multiplication and the remainder of the division by a power of two without a unit, quite interesting things can be done. Let's start to create a spell with one byte. For convenience, we denote all bits of a single byte in Latin letters from “a” to “h”. Our number n takes the form:

Multiplying n '= n⋅0x010101 (so, through the prefix "0x", I denote hexadecimal numbers) does nothing more than "replicating" one byte in triplicate:
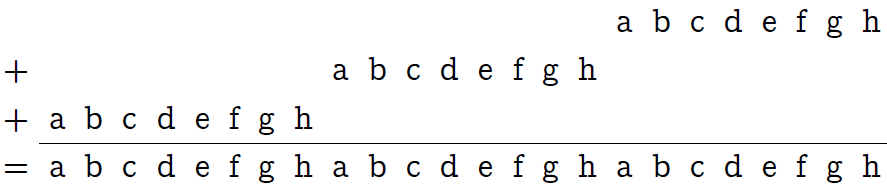
Now let's mentally divide our 24 bits into 8 blocks with 3 bits in each (see the following picture, the first line of the table). Then, using the bitwise “and” with the mask 0x249249 (the second line of the table), we reset two high-order bits in each block.

The third row of the table explains the hexadecimal mask entry. The last line shows the result we achieved: all the bits of the original byte are each contained in its three-bit block, but in a different order (the order is not important to us).
Now attention: we have to add these 8 blocks - and we get the sum of our bits!
It turns out that the remainder of dividing a number A by 2 k -1 just gives the sum of the k-bit blocks of the number A, also taken modulo 2 k -1.
That is, we need to take the remainder of the division by 2 3 -1 (seven) from the number we received, and we get the sum of our 8 blocks modulo 7. The trouble is that the sum of bits can be equal to 7 or 8, in which case the algorithm will give 0 and 1, respectively. But let's see: in which case can we get an answer of 8? Only when n = 255. And in what case can we get 0? Only when n = 0. Therefore, if the algorithm after taking the remainder by 7 gives 0, then either we received n = 0 at the input, or among exactly 7 unit bits. Summing up this reasoning, we get the following code:
In the case when n has a size of 16 bits, you can split it into two parts of 8 bits each. For example:
For the case of 32-bit and 64-bit such a division does not make sense even in theory, multiplication and the remainder of division with three branches will be too expensive if you perform them 4 or 8 times in a row. But I left empty spaces for you in the table below, so if you don’t believe me, please fill them in yourself. There are likely to be results comparable to the CountBits1 procedure, if you have a similar processor (I’m not saying that optimization with SSE is possible here, this will be a different matter).
This trick, of course, can be done without branching, but then we need that when dividing a number into blocks into a block, all numbers from 0 to 8 fit together, and this can be achieved only in the case of 4-bit blocks (and more). To perform the summation of 4-bit blocks, you need to pick up a multiplier that will allow you to correctly "propagate" the number and take the remainder of the division by 2 4 -1 = 15 to add the resulting blocks. An experienced alchemist (who knows mathematics) will easily select such a factor: 0x08040201. Why is he chosen this way?

The fact is that we need all the bits of the original number to occupy the correct positions in their 4-bit blocks (picture above), and since 8 and 4 are not mutually simple numbers, the usual copying of 8 bits 4 times will not give the correct location of the necessary bits. We have to add one zero to our byte, that is, to replicate 9 bits, since 9 is mutually simple with 4. So we get a number that has a size of 36 bits, but in which all the bits of the original byte are in lower positions of 4-bit blocks. It remains only to take the bitwise "and" with the number 0x111111111 (the second line in the picture above), in order to reset the three high-order bits in each block. Then the blocks need to be folded.
With this approach, the program of counting single bits in a byte will be extremely simple:
The drawback of the program is obvious: it requires an output to 64-bit arithmetic with all the ensuing consequences. It can be noted that in reality this program uses only 33 bits out of 64 (the upper 3 bits are zeroed), and in principle it is possible to figure out how to transfer these calculations to 32-bit arithmetic, but stories about such optimizations are not included in this topic. leadership. Let's just learn the techniques for now, and you will have to optimize them yourself for a specific task.
We will answer the question of how large the variable n can be in order for this trick to work correctly for it. As soon as we take the remainder of division by 15, such a variable cannot have a size greater than 14 bits, otherwise we will have to apply branching, as we did before. But for 14 bits, reception works if you add one zero to the 14 bits so that all the bits take up their positions. Now I will assume that you have learned the essence of the reception as a whole and can easily select the multiplier for replication and the mask for zeroing out the unnecessary bits. I will show the finished result immediately.
This program above shows what the code might look like if you had a variable of 14 bits in size without a sign. The same code will work with a variable of 15 bits, but provided that the maximum is only 14 of them equal to one, or if the case where n = 0x7FFF we analyze separately. This is all you need to understand in order to write the correct code for a variable of type u16. The idea is to “bite off” the low bit first, count the bits in the remaining 15-bit number, and then add the “bit off” bit back.
For n 32 bits, you have to conjure up with a more serious face ... First, the answer fits only 6 bits, but you can consider a separate case when n = 2 32 -1 and calmly make calculations in fields of 5 bits. This saves space and allows us to split the 32-bit field of the number n into 3 parts with 12 bits in each (yes, the last field will be incomplete). Since 12⋅5 = 60, we can replicate one 12-bit field 5 times, pick up a multiplier, and then add 5-bit blocks, taking the remainder from division by 31. You need to do this 3 times for each field. Summing up the result, we get the following code:
Here, in the same way, instead of three branches, it was possible to take 3 residues from division, but I chose the branchy option, it will work better on my processor.
For n 64 bits in size I did not manage to invent a suitable spell in which there would not be so many multiplications and additions. It turned out either 6 or 7, and this is too much for such a task. Another option is access to 128-bit arithmetic, and this is no longer understand what kind of “rollback” for us will turn back, an untrained magician can also throw away to the wall :)
Let's look at the time of work.
An obvious conclusion from this table is that 64-bit arithmetic is poorly perceived in 32-bit execution mode, although in general, the algorithm is not bad. If we recall the speed of the pre-counting algorithm in x64 mode for a single-byte table for the case of u32 (24.79 s), we find that this algorithm is only 25% behind, and this is the reason for the competition embodied in the next section.
The disadvantage of taking a residue is obvious to everyone. This is division, and division is long. Of course, modern compilers know alchemy and know how to replace division by multiplication with a shift, and to get the remainder, you need to subtract from the dividend the particular multiplied by the divisor. However, it is still long! It turns out that in the ancient scrolls of the spellcasters of the code there is one interesting way of optimizing the previous algorithm.We can sum up the k-bit blocks by not taking the remainder of the division, but by another multiplication by the mask, with which the extra bits in the blocks are zeroed out. Here’s what it looks like for n 1 bytes.
To begin with, we replicate the byte three times and delete the two high-order bits from each 3-bit block using the formula 0x010101⋅n & 0x249249 already completed.

For convenience, I marked each three-bit block with a capital Latin letter. Now multiply the result by the same mask 0x249249. The mask contains a single bit in every 3rd position, so this multiplication is equivalent to adding the number itself with itself 8 times, each time with a shift of 3 bits:
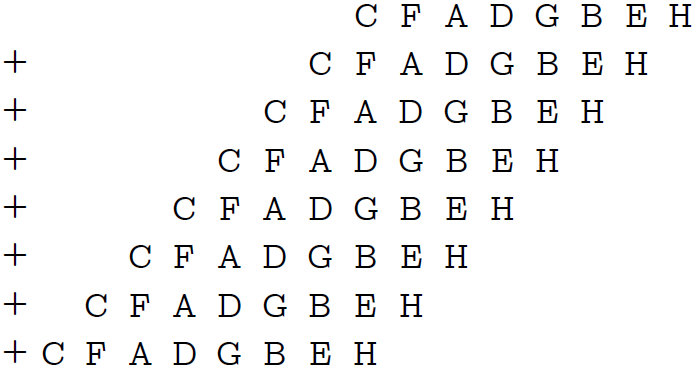
What do we see?Bits 21 through 23 give us the right amount! At the same time, overflow in any of the blocks on the right is impossible, since there will not be a number greater than 7 in any block. The only problem is that if our sum is equal to 8, we will get 0, but that’s okay The case can be considered separately.
In fact, we took the code from the previous section and replaced it with taking the remainder of dividing by 7 by multiplication, shift and bitwise "AND" at the end. At the same time, instead of 3 branches, only one remained.
To create a similar program for 16 bits, we need to take the code from the previous section, which shows how to do this by taking the remainder of division by 15 and replace this procedure with multiplication. In this case, it is not difficult to notice what conditions can be removed from the code.
For 32 bits, we do the same thing: we take the code from the previous section and, having painted a little on paper, we understand what the shift will be if we replace the remainder by multiplication.
For 64 bits, I also could not think of something that would not force my processor to perform the role of the stove.
Pleasantly surprised by the results for the x64 mode. As expected, we have overtaken the pre-count with a single-byte table for the case of u32. Is it even possible to overtake the pre-submission? Good question :)
Perhaps this is the most common trick that very often not quite experienced spellcasters repeat one after another, not understanding how it works.
Let's start with 1 byte. A byte consists of 4 fields of 2 bits each, first sum up the bits in these fields, saying something like:
Here is an explanatory picture of this operation (as before, we denote the bits of one byte by the first Latin letters):
One of the bitwise "And" leaves only the low bits of each two-bit block, the second leaves the high-order bits, but shifts them to the positions corresponding to the low-order bits. As a result of summation, we get the sum of adjacent bits in each two-bit block (the last line in the picture above).
Now add pairs of numbers in two-bit fields, putting the result in 2 four-bit fields:
The following picture explains the result. I quote it now without further ado:
Finally, we add two numbers in four-bit fields:
Acting by analogy, you can extend the reception to any number of bits equal to the power of two. The number of lines of the spell equals the binary logarithm of the number of bits. Having caught the idea, take a casual look at the 4 functions, written below, to make sure that your understanding is correct.
At this parallel summation does not end. The idea allows us to develop the observation that the same bitmask is used twice in each line, which seems to suggest “is it possible somehow to perform the bitwise“ AND ”only once?”. It is possible, but not immediately. Here is what you can do if you take the code for u32 as an example (see the comments).
As an exercise, I would like to suggest that you prove yourself why the following code will be an exact mapping of the previous one. For the first line, I give a hint, but do not look at it immediately:
Similar optimization options are possible for other data types.
Below are two tables: one for the usual parallel summation, and the second for the optimized.
In general, we see that the optimized algorithm works well, but loses to the usual in x86 mode for u64.
We see that the best options for calculating unit bits are the parallel method (with optimization) and the multiplication multiplication method for calculating the sum of blocks. We can combine both methods by obtaining a combined algorithm.
The first thing to do is execute the first three lines of the parallel algorithm. This will give us the exact amount of bits in each byte of the number. For example, for u32, do the following:
Now our number n consists of 4 bytes, which should be considered as 4 numbers, the sum of which we are looking for:

We can find the sum of these 4 bytes, if we multiply the number n by 0x01010101. You now understand well what this multiplication means, for the convenience of determining the position in which the answer will be, I quote a picture:

The answer is in 3-byte (if you count them from 0). Thus, the combined reception for u32 will look like this:
Same for u16:
Same for u64:
The speed of this method, you can see immediately in the summary table.
I invite the reader to independently draw his conclusions, having studied the two tables below. In them I indicated the name of the methods, the programs to which we implemented, and also marked with a rectangular frame those approaches that I consider the best in each specific case. Those who thought that the precontest always wins, expect a slight surprise for the x64 mode.
Final comparison for x86 compilation mode.
Final comparison for x64 compilation mode.
In no case do not consider the final table as evidence in favor of one or another approach. Believe that on your processor and with your compiler some numbers in such a table will be completely different. Unfortunately, we can never say for sure which of the algorithms will be better in one way or another. For each task, you need to sharpen a specific method, and, unfortunately, there is no universal fast algorithm.
I have outlined the ideas that I know about myself, but these are only ideas, the specific implementations of which in different combinations can be very different. By combining these ideas in different ways, you can get a huge number of different algorithms for calculating single bits, each of which may well be good in some way.
Thanks for attention. See you again!
UPD : The POPCNT instruction from SSE4.2 is not included in the testing list, because I do not have a processor that supports SSE4.2.
Before we begin, I just want to warn you that this article is not for beginners in programming. I need the reader to have a general idea of the simplest bit operations (bitwise "and", "or", shift), to have a good hexadecimal numbering system and to use the imagination quite confidently, presenting in it not always short bit sequences. If possible, everything will be accompanied by pictures, but you know, they only simplify, but do not replace the full presentation.
')
All described techniques were implemented in C language and tested in two modes: 32 and 64 bits. Thus, for a more complete understanding of the article, it would be better that you at least approximately understand the C language. Testing took place on the processor Core 2 Duo E8400 @ 3GHz on 64-bit Windows 7. Measurement of the net operating time of the programs was carried out using the runexe utility. All source codes of the described algorithms are available in the archive on the Yandex disk, their compilation is checked for compilers Visual C ++, Intel C ++, GCC and CLang, so in principle, you should have no problems if someone wants to double-check the results with them. Linux users, I think, know better than me how to test the program runtime on their system, so I don’t give them any advice.
Among the readers, there may be people who find it easier to watch the same thing on the video. I recorded such a video (58 minutes), in which the presentation format is exactly the same, which will be lower in the text, but maybe in a slightly different style, more dry and strictly, while I tried to revive the text a little. Therefore, study the material as it is more convenient to whom.
Watch the video
Now the algorithms generated by one or another set of alchemical methods will be sequentially described, in each section there will be a table comparing the working time for variables of different sizes, and at the end there will be a summary table for all algorithms. All algorithms use pseudonyms for unsigned numbers from 8 to 64 bits.
typedef unsigned char u8; typedef unsigned short int u16; typedef unsigned int u32; typedef unsigned long long u64; Naive approach
It is obvious that bit alchemy is not used to shine at the interview, but with the aim of significantly accelerating the programs. Acceleration in relation to what? In relation to the trivial techniques that can come to mind when there is no time to go into the task in more detail. This is the naive approach to calculating bits: we simply “bite off” one bit after another and add them up by repeating the procedure until the number is zero.
u8 CountOnes0 (u8 n) { u8 res = 0; while (n) { res += n&1; n >>= 1; } return res; } I do not see any reason to comment on this trivial cycle. With the naked eye it is clear that if the high bit of the number n is 1, then the cycle will have to go through all the bits of the number before it reaches the high bit.
Changing the type of the input parameter u8 to u16, u32 and u64 we get 4 different functions. Let's test each of them on a stream of 2 32 numbers given in a chaotic order. It is clear that for u8 we have 256 different input data, but for consistency we still run 2 32 random numbers for all these and all subsequent functions, always in the same order (for details you can refer to the curriculum code from the archive ).
The time in the table below is in seconds. For testing, the program was run three times and the average time was selected. The error hardly exceeds 0.1 seconds. The first column reflects the compiler mode (32-bit source code or 64-bit), then 4 columns are responsible for 4 variants of input data.
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 38.18 | 72.00 | 130.49 | 384.76 |
| x64 | 37.72 | 71.51 | 131.47 | 227.46 |
As we see, the speed of work quite naturally increases with increasing size of the input parameter. The variant when the numbers are 64 bits in size and the calculation is in x86 mode is a little out of general regularity. It's clear that the processor is forced to do fourfold work by doubling the input parameter, and it’s even good that it only copes three times slower.
The first benefit of this approach is that when it is implemented it is difficult to make a mistake, therefore, a program written in this way can become a reference for testing more complex algorithms (this was exactly what was done in my case). The second benefit is versatility and relatively simple portability for numbers of any size.
The trick with "biting off" the younger single bits
This alchemical method is based on the idea of zeroing the low-order single bit. Having the number n, we can cast the spell n = n & (n-1), taking the younger one from the number n. The picture below for n = 232 will clarify the situation for people who first learned about this trick.

The program code has not changed much.
u8 CountOnes1 (u8 n) { u8 res = 0; while (n) { res ++; n &= n-1; // . } return res; } Now the cycle will be executed exactly as many times as the units in the number n. This does not eliminate the worst case when all the bits in a single number, but significantly reduces the average number of iterations. Will this approach greatly ease the processor's pain? In fact, not much, but for 8 bits it will be even worse. Let me remind you that the summary table of results will be at the end, and here in each section will be its own table.
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 44.73 | 55,88 | 72.02 | 300.78 |
| x64 | 40.96 | 69,16 | 79.13 | 126.72 |
Preliminary account
Let's not rush to move to the "hard" spells, consider the last simple technique that can save even the most inexperienced magician. This solution is not directly related to bit alchemy, but for the sake of completeness, it should be considered without fail. Let's get two tables for 256 and 65536 values, in which the answers for all possible 1-byte and 2-byte values are calculated in advance, respectively.
u8 BitsSetTableFF[256]; // u8 BitsSetTableFFFF[65536]; // Now the program for 1 byte will look like this
u8 CountOnes2_FF (u8 n) { return BitsSetTableFF[n]; } To calculate the number of bits in larger numbers, they need to be divided into bytes. For example, for u32 there could be such code:
u8 CountOnes2_FF (u32 n) { u8 *p = (u8*)&n; n = BitsSetTableFF[p[0]] + BitsSetTableFF[p[1]] + BitsSetTableFF[p[2]] + BitsSetTableFF[p[3]]; return n; } Or such, if we use the table of predalagment for 2 bytes:
u8 CountOnes2_FFFF (u32 n) { u16 *p = (u16*)&n; n = BitsSetTableFFFF[p[0]] + BitsSetTableFFFF[p[1]]; return n; } Well, then you guessed it, for each option of the size of the input parameter n (except 8 bits) there can be two versions of the pre-calculation, depending on which of the two tables we use. I think the reader understands why we cannot just take and start the BitsSetTableFFFFFFFF table, but there may well be problems where this will be justified.
Does the pre-submission work fast? It all depends on the size, see the table below. The first is for a single byte precondition, and the second is for two byte.
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 0.01 | 1.83 | 21.07 | 36.25 |
| x64 | 0.01 | 1.44 | 24.79 | 26.84 |
An interesting point: for the x64 mode, the pre-account for u64 works much faster, perhaps it is optimization features, although this does not appear in the second case.
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | --- | 0.05 | 7.95 | 13.01 |
| x64 | --- | 0.07 | 8.49 | 13.01 |
Important note: this algorithm using the pre-calculation is beneficial only if the following two conditions are met: (1) you have extra memory, (2) you need to perform the calculation of the number of single bits much more than the size of the table itself, that is, you can “Play” the time spent on pre-filling the table with some of the simple algorithms. Perhaps you can also keep in mind the exotic condition, which in practice is always fulfilled. You must ensure that the memory access itself is fast and does not slow down other functions of the system. The fact is that accessing the table can throw out from the cache what was originally there and thus slow down some other part of the code. You can hardly find a jamb quickly, but such monstrous optimizations are hardly necessary for anyone to practice in the implementation of ordinary programs.
Multiplication and remainder of division
Finally, take the stronger potions from our alchemy shelf. With the help of multiplication and the remainder of the division by a power of two without a unit, quite interesting things can be done. Let's start to create a spell with one byte. For convenience, we denote all bits of a single byte in Latin letters from “a” to “h”. Our number n takes the form:

Multiplying n '= n⋅0x010101 (so, through the prefix "0x", I denote hexadecimal numbers) does nothing more than "replicating" one byte in triplicate:
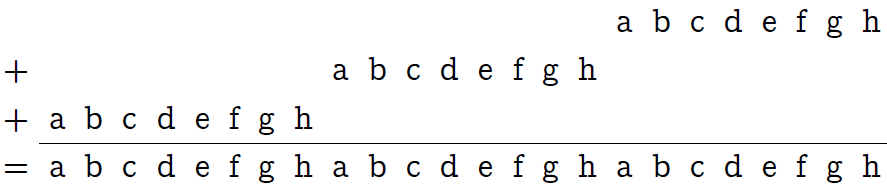
Now let's mentally divide our 24 bits into 8 blocks with 3 bits in each (see the following picture, the first line of the table). Then, using the bitwise “and” with the mask 0x249249 (the second line of the table), we reset two high-order bits in each block.

The third row of the table explains the hexadecimal mask entry. The last line shows the result we achieved: all the bits of the original byte are each contained in its three-bit block, but in a different order (the order is not important to us).
Now attention: we have to add these 8 blocks - and we get the sum of our bits!
It turns out that the remainder of dividing a number A by 2 k -1 just gives the sum of the k-bit blocks of the number A, also taken modulo 2 k -1.
Proof
Divide the number A (in binary notation) into blocks of k bits in each (if necessary, you can add the latest, most significant, block of zeros). Denote by A i the i-th block. Now we write the value of the number A through the sum of these blocks, multiplied by the corresponding power of two:
A = A 0 ⋅ 2 0 ⋅ k + A 1 ⋅ 2 1 ⋅ k + ... + A N-1 ⋅ 2 (N-1) ⋅ k ,
where N is the number of blocks.
Now let's calculate A mod (2 k -1).
A mod (2 k -1) = (A 0 ⋅ 2 0 ⋅ k + A 1 ⋅ 2 1 ⋅ k + ... + A N-1 ⋅ 2 (N-1) ⋅ k ) mod (2 k -1) = (A 0 + A 1 + ... + A N-1 ) mod (2 k -1).
This is due to the fact that 2 i⋅k = 1 (mod (2 k -1)) for any non-negative integer i. (True, it is important here that the trick makes sense when k> 1, otherwise it’s not quite clear how we interpret module 1). So we got the sum of blocks modulo 2 k -1.
A = A 0 ⋅ 2 0 ⋅ k + A 1 ⋅ 2 1 ⋅ k + ... + A N-1 ⋅ 2 (N-1) ⋅ k ,
where N is the number of blocks.
Now let's calculate A mod (2 k -1).
A mod (2 k -1) = (A 0 ⋅ 2 0 ⋅ k + A 1 ⋅ 2 1 ⋅ k + ... + A N-1 ⋅ 2 (N-1) ⋅ k ) mod (2 k -1) = (A 0 + A 1 + ... + A N-1 ) mod (2 k -1).
This is due to the fact that 2 i⋅k = 1 (mod (2 k -1)) for any non-negative integer i. (True, it is important here that the trick makes sense when k> 1, otherwise it’s not quite clear how we interpret module 1). So we got the sum of blocks modulo 2 k -1.
That is, we need to take the remainder of the division by 2 3 -1 (seven) from the number we received, and we get the sum of our 8 blocks modulo 7. The trouble is that the sum of bits can be equal to 7 or 8, in which case the algorithm will give 0 and 1, respectively. But let's see: in which case can we get an answer of 8? Only when n = 255. And in what case can we get 0? Only when n = 0. Therefore, if the algorithm after taking the remainder by 7 gives 0, then either we received n = 0 at the input, or among exactly 7 unit bits. Summing up this reasoning, we get the following code:
u8 CountOnes3 (u8 n) { if (n == 0) return 0; // , 0. if (n == 0xFF) return 8; // , 8. n = (0x010101*n & 0x249249) % 7; // 7. if (n == 0) return 7; // 7 . return n; // , 1 6 . } In the case when n has a size of 16 bits, you can split it into two parts of 8 bits each. For example:
u8 CountOnes3 (u16 n) { return CountOnes3 (u8(n&0xFF)) + CountOnes3 (u8(n>>8)); For the case of 32-bit and 64-bit such a division does not make sense even in theory, multiplication and the remainder of division with three branches will be too expensive if you perform them 4 or 8 times in a row. But I left empty spaces for you in the table below, so if you don’t believe me, please fill them in yourself. There are likely to be results comparable to the CountBits1 procedure, if you have a similar processor (I’m not saying that optimization with SSE is possible here, this will be a different matter).
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 12.42 | 30.57 | --- | --- |
| x64 | 13.88 | 33.88 | --- | --- |
This trick, of course, can be done without branching, but then we need that when dividing a number into blocks into a block, all numbers from 0 to 8 fit together, and this can be achieved only in the case of 4-bit blocks (and more). To perform the summation of 4-bit blocks, you need to pick up a multiplier that will allow you to correctly "propagate" the number and take the remainder of the division by 2 4 -1 = 15 to add the resulting blocks. An experienced alchemist (who knows mathematics) will easily select such a factor: 0x08040201. Why is he chosen this way?

The fact is that we need all the bits of the original number to occupy the correct positions in their 4-bit blocks (picture above), and since 8 and 4 are not mutually simple numbers, the usual copying of 8 bits 4 times will not give the correct location of the necessary bits. We have to add one zero to our byte, that is, to replicate 9 bits, since 9 is mutually simple with 4. So we get a number that has a size of 36 bits, but in which all the bits of the original byte are in lower positions of 4-bit blocks. It remains only to take the bitwise "and" with the number 0x111111111 (the second line in the picture above), in order to reset the three high-order bits in each block. Then the blocks need to be folded.
With this approach, the program of counting single bits in a byte will be extremely simple:
u8 CountOnes3_x64 (u8 n) { return ((u64)0x08040201*n & 0x111111111) % 15; } The drawback of the program is obvious: it requires an output to 64-bit arithmetic with all the ensuing consequences. It can be noted that in reality this program uses only 33 bits out of 64 (the upper 3 bits are zeroed), and in principle it is possible to figure out how to transfer these calculations to 32-bit arithmetic, but stories about such optimizations are not included in this topic. leadership. Let's just learn the techniques for now, and you will have to optimize them yourself for a specific task.
We will answer the question of how large the variable n can be in order for this trick to work correctly for it. As soon as we take the remainder of division by 15, such a variable cannot have a size greater than 14 bits, otherwise we will have to apply branching, as we did before. But for 14 bits, reception works if you add one zero to the 14 bits so that all the bits take up their positions. Now I will assume that you have learned the essence of the reception as a whole and can easily select the multiplier for replication and the mask for zeroing out the unnecessary bits. I will show the finished result immediately.
u8 CountOnes3_x64 (u14 n) { // ( )! return (n*0x200040008001llu & 0x111111111111111llu) % 15; } This program above shows what the code might look like if you had a variable of 14 bits in size without a sign. The same code will work with a variable of 15 bits, but provided that the maximum is only 14 of them equal to one, or if the case where n = 0x7FFF we analyze separately. This is all you need to understand in order to write the correct code for a variable of type u16. The idea is to “bite off” the low bit first, count the bits in the remaining 15-bit number, and then add the “bit off” bit back.
u8 CountOnes3_x64 (u16 n) { u8 leastBit = n&1; // . n >>= 1; // 15 . if (n == 0) return leastBit; // 0, . if (n == 0x7FFF) return leastBit + 15; // , 15+ . return leastBit + (n*0x200040008001llu & 0x111111111111111llu) % 15; // ( 14+ ). } For n 32 bits, you have to conjure up with a more serious face ... First, the answer fits only 6 bits, but you can consider a separate case when n = 2 32 -1 and calmly make calculations in fields of 5 bits. This saves space and allows us to split the 32-bit field of the number n into 3 parts with 12 bits in each (yes, the last field will be incomplete). Since 12⋅5 = 60, we can replicate one 12-bit field 5 times, pick up a multiplier, and then add 5-bit blocks, taking the remainder from division by 31. You need to do this 3 times for each field. Summing up the result, we get the following code:
u8 CountOnes3_x64 ( u32 n ) { if (n == 0) return 0; if (n + 1 == 0) return 32; u64 res = (n&0xFFF)*0x1001001001001llu & 0x84210842108421llu; res += ((n&0xFFF000)>>12)*0x1001001001001llu & 0x84210842108421llu; res += (n>>24)*0x1001001001001llu & 0x84210842108421llu; res %= 0x1F; if (res == 0) return 31; return res; } Here, in the same way, instead of three branches, it was possible to take 3 residues from division, but I chose the branchy option, it will work better on my processor.
For n 64 bits in size I did not manage to invent a suitable spell in which there would not be so many multiplications and additions. It turned out either 6 or 7, and this is too much for such a task. Another option is access to 128-bit arithmetic, and this is no longer understand what kind of “rollback” for us will turn back, an untrained magician can also throw away to the wall :)
Let's look at the time of work.
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 39.78 | 60.48 | 146.78 | --- |
| x64 | 6.78 | 12.28 | 31.12 | --- |
An obvious conclusion from this table is that 64-bit arithmetic is poorly perceived in 32-bit execution mode, although in general, the algorithm is not bad. If we recall the speed of the pre-counting algorithm in x64 mode for a single-byte table for the case of u32 (24.79 s), we find that this algorithm is only 25% behind, and this is the reason for the competition embodied in the next section.
Replacing taking remainder by multiplication and shift
The disadvantage of taking a residue is obvious to everyone. This is division, and division is long. Of course, modern compilers know alchemy and know how to replace division by multiplication with a shift, and to get the remainder, you need to subtract from the dividend the particular multiplied by the divisor. However, it is still long! It turns out that in the ancient scrolls of the spellcasters of the code there is one interesting way of optimizing the previous algorithm.We can sum up the k-bit blocks by not taking the remainder of the division, but by another multiplication by the mask, with which the extra bits in the blocks are zeroed out. Here’s what it looks like for n 1 bytes.
To begin with, we replicate the byte three times and delete the two high-order bits from each 3-bit block using the formula 0x010101⋅n & 0x249249 already completed.

For convenience, I marked each three-bit block with a capital Latin letter. Now multiply the result by the same mask 0x249249. The mask contains a single bit in every 3rd position, so this multiplication is equivalent to adding the number itself with itself 8 times, each time with a shift of 3 bits:
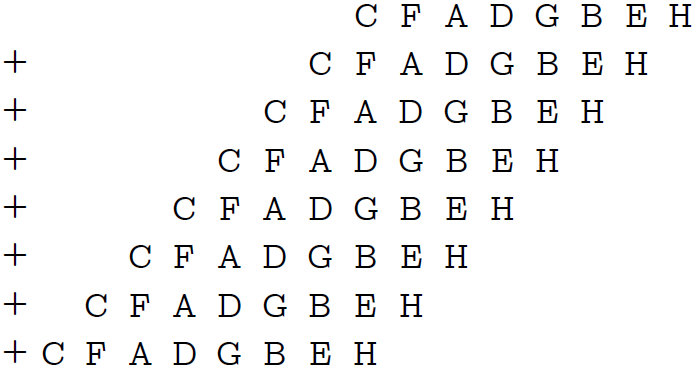
What do we see?Bits 21 through 23 give us the right amount! At the same time, overflow in any of the blocks on the right is impossible, since there will not be a number greater than 7 in any block. The only problem is that if our sum is equal to 8, we will get 0, but that’s okay The case can be considered separately.
u8 CountOnes3_x64_m (u8 n) { if (n == 0xFF) return 8; return ((u64(0x010101*n & 0x249249) * 0x249249) >> 21) & 0x7; } In fact, we took the code from the previous section and replaced it with taking the remainder of dividing by 7 by multiplication, shift and bitwise "AND" at the end. At the same time, instead of 3 branches, only one remained.
To create a similar program for 16 bits, we need to take the code from the previous section, which shows how to do this by taking the remainder of division by 15 and replace this procedure with multiplication. In this case, it is not difficult to notice what conditions can be removed from the code.
u8 CountOnes3_x64_m (u16 n) { u8 leastBit = n&1; // n >>= 1; // 15 . return leastBit + (( (n*0x200040008001llu & 0x111111111111111llu)*0x111111111111111llu >> 56) & 0xF); // ( 15 + ). } For 32 bits, we do the same thing: we take the code from the previous section and, having painted a little on paper, we understand what the shift will be if we replace the remainder by multiplication.
u8 CountOnes3_x64_m ( u32 n ) { if (n+1 == 0) return 32; u64 res = (n&0xFFF)*0x1001001001001llu & 0x84210842108421llu; res += ((n&0xFFF000)>>12)*0x1001001001001llu & 0x84210842108421llu; res += (n>>24)*0x1001001001001llu & 0x84210842108421llu; return (res*0x84210842108421llu >> 55) & 0x1F; } For 64 bits, I also could not think of something that would not force my processor to perform the role of the stove.
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 12.66 | 42.37 | 99.90 | --- |
| x64 | 3.54 | 4.51 | 18.35 | --- |
Pleasantly surprised by the results for the x64 mode. As expected, we have overtaken the pre-count with a single-byte table for the case of u32. Is it even possible to overtake the pre-submission? Good question :)
Parallel summation
Perhaps this is the most common trick that very often not quite experienced spellcasters repeat one after another, not understanding how it works.
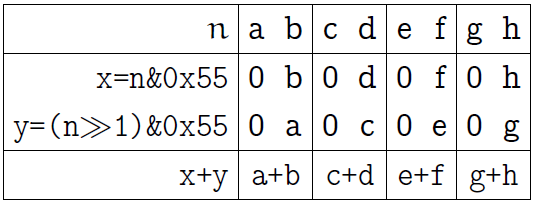
Let's start with 1 byte. A byte consists of 4 fields of 2 bits each, first sum up the bits in these fields, saying something like:
n = (n>>1)&0x55 + (n&0x55); Here is an explanatory picture of this operation (as before, we denote the bits of one byte by the first Latin letters):

One of the bitwise "And" leaves only the low bits of each two-bit block, the second leaves the high-order bits, but shifts them to the positions corresponding to the low-order bits. As a result of summation, we get the sum of adjacent bits in each two-bit block (the last line in the picture above).
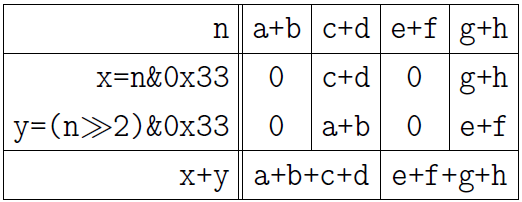
Now add pairs of numbers in two-bit fields, putting the result in 2 four-bit fields:
n = (n>>2)&0x33 + (n&0x33); The following picture explains the result. I quote it now without further ado:

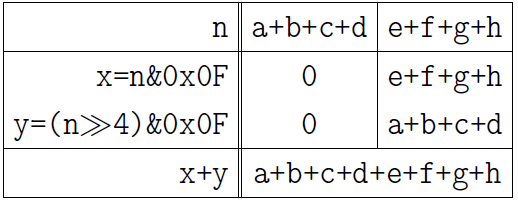
Finally, we add two numbers in four-bit fields:
n = (n>>4)&0x0F + (n&0x0F); 
Acting by analogy, you can extend the reception to any number of bits equal to the power of two. The number of lines of the spell equals the binary logarithm of the number of bits. Having caught the idea, take a casual look at the 4 functions, written below, to make sure that your understanding is correct.
u8 CountOnes4 (u8 n) { n = ((n>>1) & 0x55) + (n & 0x55); n = ((n>>2) & 0x33) + (n & 0x33); n = ((n>>4) & 0x0F) + (n & 0x0F); return n; } u8 CountOnes4 (u16 n) { n = ((n>>1) & 0x5555) + (n & 0x5555); n = ((n>>2) & 0x3333) + (n & 0x3333); n = ((n>>4) & 0x0F0F) + (n & 0x0F0F); n = ((n>>8) & 0x00FF) + (n & 0x00FF); return n; } u8 CountOnes4 (u32 n) { n = ((n>>1) & 0x55555555) + (n & 0x55555555); n = ((n>>2) & 0x33333333) + (n & 0x33333333); n = ((n>>4) & 0x0F0F0F0F) + (n & 0x0F0F0F0F); n = ((n>>8) & 0x00FF00FF) + (n & 0x00FF00FF); n = ((n>>16) & 0x0000FFFF) + (n & 0x0000FFFF); return n; } u8 CountOnes4 (u64 n) { n = ((n>>1) & 0x5555555555555555llu) + (n & 0x5555555555555555llu); n = ((n>>2) & 0x3333333333333333llu) + (n & 0x3333333333333333llu); n = ((n>>4) & 0x0F0F0F0F0F0F0F0Fllu) + (n & 0x0F0F0F0F0F0F0F0Fllu); n = ((n>>8) & 0x00FF00FF00FF00FFllu) + (n & 0x00FF00FF00FF00FFllu); n = ((n>>16) & 0x0000FFFF0000FFFFllu) + (n & 0x0000FFFF0000FFFFllu); n = ((n>>32) & 0x00000000FFFFFFFFllu) + (n & 0x00000000FFFFFFFFllu); return n; } At this parallel summation does not end. The idea allows us to develop the observation that the same bitmask is used twice in each line, which seems to suggest “is it possible somehow to perform the bitwise“ AND ”only once?”. It is possible, but not immediately. Here is what you can do if you take the code for u32 as an example (see the comments).
u8 CountOnes4 (u32 n) { n = ((n>>1) & 0x55555555) + (n & 0x55555555); // n = ((n>>2) & 0x33333333) + (n & 0x33333333); // n = ((n>>4) & 0x0F0F0F0F) + (n & 0x0F0F0F0F); // & n = ((n>>8) & 0x00FF00FF) + (n & 0x00FF00FF); // & n = ((n>>16) & 0x0000FFFF) + (n & 0x0000FFFF); // & return n; // 8- . } As an exercise, I would like to suggest that you prove yourself why the following code will be an exact mapping of the previous one. For the first line, I give a hint, but do not look at it immediately:
hint
ab 2a+b, …?
u8 CountOnes4_opt (u32 n) { n -= (n>>1) & 0x55555555; n = ((n>>2) & 0x33333333 ) + (n & 0x33333333); n = ((n>>4) + n) & 0x0F0F0F0F; n = ((n>>8) + n) & 0x00FF00FF; n = ((n>>16) + n); return n; } Similar optimization options are possible for other data types.
Below are two tables: one for the usual parallel summation, and the second for the optimized.
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 7.52 | 14.10 | 21,12 | 62.70 |
| x64 | 8.06 | 11.89 | 21.30 | 22,59 |
| Mode | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 7.18 | 11.89 | 18.86 | 65.00 |
| x64 | 8.09 | 10.27 | 19.20 | 19.20 |
In general, we see that the optimized algorithm works well, but loses to the usual in x86 mode for u64.
Combined method
We see that the best options for calculating unit bits are the parallel method (with optimization) and the multiplication multiplication method for calculating the sum of blocks. We can combine both methods by obtaining a combined algorithm.
The first thing to do is execute the first three lines of the parallel algorithm. This will give us the exact amount of bits in each byte of the number. For example, for u32, do the following:
n -= (n>>1) & 0x55555555; n = ((n>>2) & 0x33333333) + (n & 0x33333333); n = (((n>>4) + n) & 0x0F0F0F0F ); Now our number n consists of 4 bytes, which should be considered as 4 numbers, the sum of which we are looking for:

We can find the sum of these 4 bytes, if we multiply the number n by 0x01010101. You now understand well what this multiplication means, for the convenience of determining the position in which the answer will be, I quote a picture:

The answer is in 3-byte (if you count them from 0). Thus, the combined reception for u32 will look like this:
u8 CountOnes5 ( u32 n ) { n -= (n>>1) & 0x55555555; n = ((n>>2) & 0x33333333 ) + (n & 0x33333333); n = ((((n>>4) + n) & 0x0F0F0F0F) * 0x01010101) >> 24; return n; // 8 . } Same for u16:
u8 CountOnes5 (u16 n) { n -= (n>>1) & 0x5555; n = ((n>>2) & 0x3333) + (n & 0x3333); n = ((((n>>4) + n) & 0x0F0F) * 0x0101) >> 8; return n; // 8 . } Same for u64:
u8 CountOnes5 ( u64 n ) { n -= (n>>1) & 0x5555555555555555llu; n = ((n>>2) & 0x3333333333333333llu ) + (n & 0x3333333333333333llu); n = ((((n>>4) + n) & 0x0F0F0F0F0F0F0F0Fllu) * 0x0101010101010101) >> 56; return n; // 8 . } The speed of this method, you can see immediately in the summary table.
Final comparison
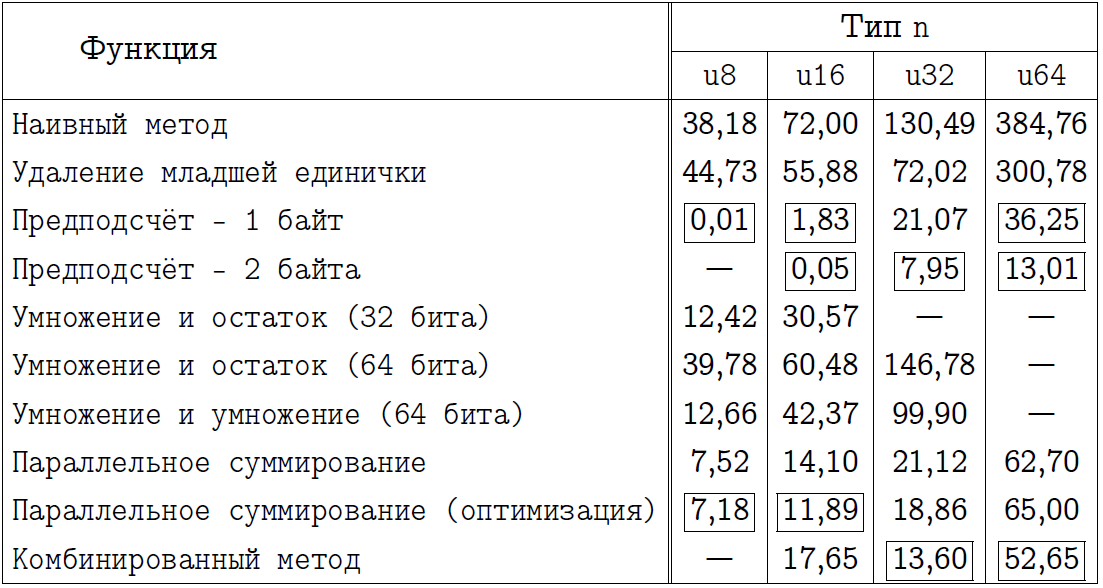
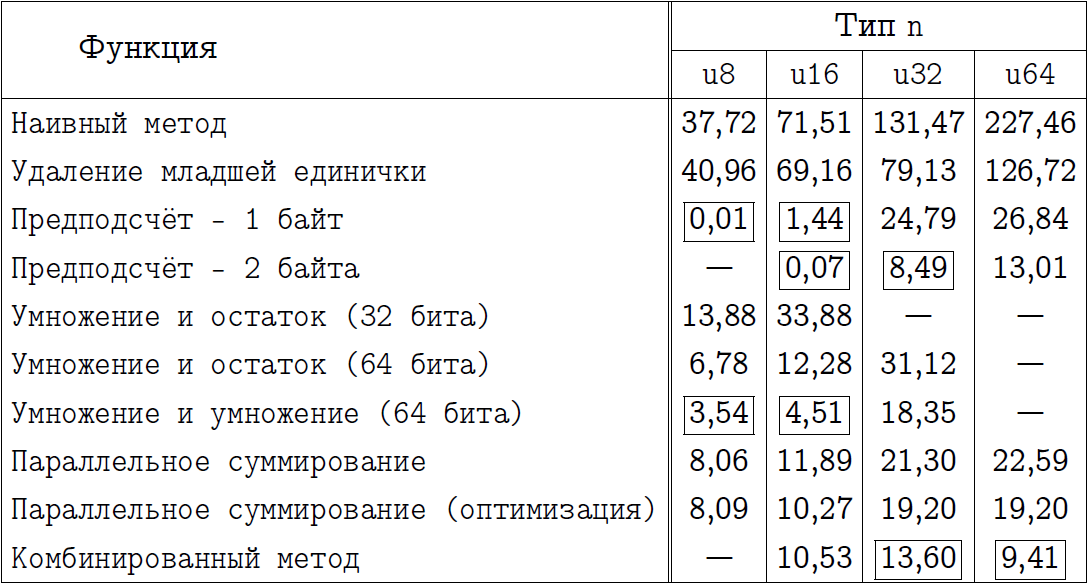
I invite the reader to independently draw his conclusions, having studied the two tables below. In them I indicated the name of the methods, the programs to which we implemented, and also marked with a rectangular frame those approaches that I consider the best in each specific case. Those who thought that the precontest always wins, expect a slight surprise for the x64 mode.
Final comparison for x86 compilation mode.

Final comparison for x64 compilation mode.

Comment
In no case do not consider the final table as evidence in favor of one or another approach. Believe that on your processor and with your compiler some numbers in such a table will be completely different. Unfortunately, we can never say for sure which of the algorithms will be better in one way or another. For each task, you need to sharpen a specific method, and, unfortunately, there is no universal fast algorithm.
I have outlined the ideas that I know about myself, but these are only ideas, the specific implementations of which in different combinations can be very different. By combining these ideas in different ways, you can get a huge number of different algorithms for calculating single bits, each of which may well be good in some way.
Thanks for attention. See you again!
UPD : The POPCNT instruction from SSE4.2 is not included in the testing list, because I do not have a processor that supports SSE4.2.
Source: https://habr.com/ru/post/276957/
All Articles