Algorithm for creating a list of all permutations or placements

At once I will make a reservation, this article is thematically similar to the non-recursive algorithm for generating permutations published about a year ago by the author of SemenovVV , but the approach here, in my opinion, is fundamentally different.



I was faced with the need to compile a list of all permutations of n elements. For n = 4 or even 5, the problem is solved manually in a matter of minutes, but for 6! = 720 and higher write pages I was already too lazy - I needed automation. I was sure that this “bicycle” had already been invented many times and in different variations, but it was interesting to find out on my own - therefore, deliberately not looking at the relevant literature, I sat down to create an algorithm.



I rejected the first version of the recursion code as too trivial and resource-intensive. Further, having made “feint ears”, I developed a not very effective algorithm, sorting out a deliberately larger number of options and sifting out only those that are suitable. It worked, but I wanted something elegant - and, starting from scratch, I began to look for patterns in the lexicographical order of permutations for small values ​​of n . The result was a neat code that, with minimal “strapping”, can be represented in Python as 10 lines (see below). Moreover, this approach works not only for permutations, but also for allocating n elements in m positions (in the case when n ≥ m ).

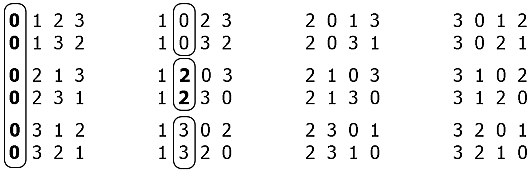
If you look at the list of all permutations for 4 to 4, then a certain structure is noticeable:





')

The entire array of permutations (4! = 24) can be divided into groups of (n-1)! = 3! - six permutations, and each group in turn divided into (n-1-1)! = 2! - two combinations and so on. In the considered case, when for n = 4, this is all.



So, from the point of view of lexicography, this set of permutations can be imagined as an increasing series: 0123 <0132 <... <3210, so to speak. We know in advance how many times the same element in a certain position will be repeated - this is the number of permutations for the array order by one less, i.e. (a-1)! where a is the dimension of the current array. Then the sign of the transition to the next value will be the new result of integer division (“ // ”) of the sequence number i of the combination by the number of such permutations: i // (a-1)! . Also, to determine what the number of this item will be in the list of those not yet involved (so as not to go around it in a circle), we use the remainder of the division (“ % ”) of the value obtained by the length of this list. So we have the following construction:



i // (a-1)! % r



where r is the dimension of the array of elements not yet involved.



For clarity, we consider a specific case. Of all 24 permutations i Є [0, 23] 4 elements in 4 positions, for example, the 17th will be the following sequence:



[17 // (4-1)!]% R (0,1,2,3) = 2% 4 = 2



(i.e., if counted from 0, the third element of the list is “2”). The next element of this permutation will be:



[17 // (3-1)!]% R (0,1,3) = 8% 3 = 2



(again the third element is now “3”)



If we continue in the same spirit, we end up with the array “2 3 1 0”. Therefore, looping through all the values ​​of i from the number of permutations [ n! ] or placements [ n! / (nm)! , where m is the number of positions in the array], we get an exhaustive set of the desired combinations.



Actually, the code itself looks like this:

import math elm=4 # - , n cells=4 # - , m res=[] #   arrang = math.factorial(elm)/math.factorial(elm-cells) #  -  for i in range(arrang): res.append([]) source=range(elm) #      for j in range(cells): p=i//math.factorial(cells-1-j)%len(source) res[len(res)-1].append(source[p]) source.pop(p) 

UPD: eventually I realized that the method was not sufficiently tested - so if someone starts to use it, please be vigilant (I would not want to let someone down)