Finite Volume method - implementation on the example of thermal conductivity
The article describes the implementation of the well-known finite volume method for the numerical solution of partial differential equations. It is used to divide a region into any standard elements (finite volumes) - triangles, quadrangles, etc. The method of visualizing the calculation results is also self-written.
The method is based on dividing the region into non-intersecting control volumes (elements), the nodal points where a solution is sought. Solving it - we find the values.
desired variables at nodal points. For a single element, the equation is obtained by integrating the original diff of the equation with respect to the element and approximating the integrals.
The term final volume in the article will often be replaced with the Element, for convenience we will consider them equivalent (the element in this article has nothing to do with the finite element method).
')
There are 2 different ways to solve the FVM problem:
1) the faces of the control volume coincide with the faces of the element
2) the faces of the control volume pass through the centers of the faces of the elements (into which the region is divided). The desired variables are stored at the vertices of these elements. A control volume is built around each vertex. For a non-rectangular grid, this method has 2 more subspecies.

We will use method 1) with control volumes coinciding with the elements into which the region is divided.
Some advantages of FVM:
The FVM method is implemented on the example of the heat equation:
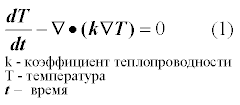
So the main steps in the implementation of FVM:
For the time derivative, we use the standard simplest method of Euler. This will be an explicit time scheme, where the sought from the previous step are taken. And at the first step, we set the initial conditions.

Using the divergence theorem, the integral of volume is transformed into an integral of area. The meaning is that we replace integration over the entire internal volume of our element with integration only over the surface of this volume. This formulation is more suitable for the 3D case. For 2D, instead of volume V - the area of the element, and instead of S - the perimeter of the element. It turns out that the integral over the area is replaced by an integral along the perimeter. In fact, the degree of derivative decreases. If, for example, there is a second derivative, then only ervaya, when was the first - instead of the derivative will be sought peremennaya.Nado just have to remember that we are dealing not with the usual derivative with a divergence.
So the second term in our equation after integration is transformed as follows:
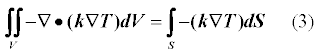

The figure shows Element C and its neighboring elements on the right (E), on the left (W), on the top (N) and on the bottom (S) . The element C has 4 faces marked with letters ewns . It is these 4 faces that make up the perimeter of the element and integration is performed. For each element, as a result, we obtain a discrete analog of the original diff equation.
Let us make a discrete analogue for element C. To begin, we need to understand the integral (3). The integral is in fact a sum. Therefore, we replace the integral over the entire surface of the element by the sum of the 4 components of this surface, ie 4 edges of the element.
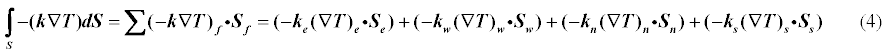
The ewns indices here mean that the expression or variable is calculated in the center of the corresponding face.
Now let's put together the resulting simplifications of the parts of the original diff equation - terms (2) and (4). We get the first approximation level:

Now we only need to approximate (4) until the end, since the gradient enters there, and we need to convert it into numerical form. In fact, this sum represents the sum of heat fluxes through the edges. Our case is simplified for a rectangular grid, because the normal to the face only 1 component remains - either along the x axis or along y.
Let us analyze this process in detail using the example of the e face.

Now we substitute instead of the sum in the equation (5) the obtained discrete analogs for 4 faces:
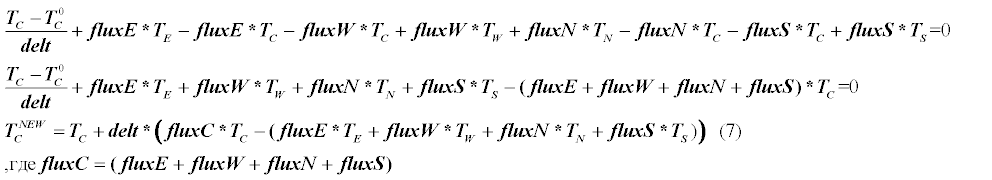
Equation (7) is the final equation for the element C, from which we obtain at each time step a new value of temperature (Tnew) in the element C.
The figure shows the element C whose face e is at the boundary and the temperature values on this face are known, either as a given temperature or as a given heat flux through the face.

We consider only 2 types of boundary conditions.
Case 2) is the simplest, since it turns out that the e face is not required at discretization (since all the coefficients are Flux = 0) and you can simply skip it.
Now consider case 1). Discretization of the edge e will be generally similar to the one that has already been described. There will be only 2 changes - instead of Te there will be a known boundary value Tb and instead of a distance DXe it will be DXe / 2. Otherwise, you can consider the value Te as if this would be an ordinary neighboring node E. Now we shall write out the term for the boundary element C in more detail.
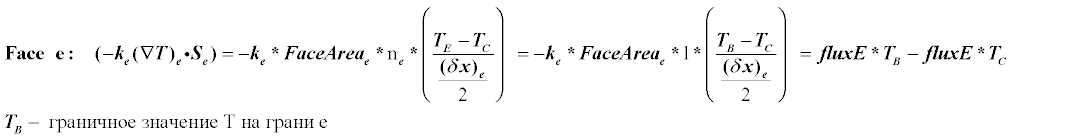
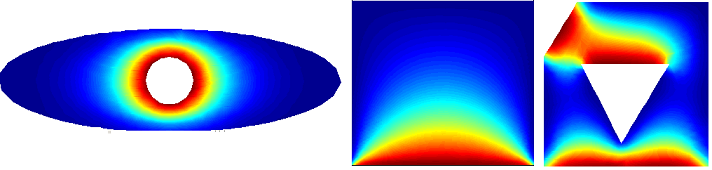
As an example, consider the area divided into 9 elements, grid 3 * 3. On the first slides, the following boundary conditions are applied: T = 0 on 3 sides, T = 240 set to the bottom. On the second slide line, on the sides, the boundary conditions with Flux are set. = 0, above T = 0, below T = 240. In each case there are 2 pictures, one with a breakdown of the area 3 * 3 elements, the second 40 * 40.

This is where the advantage of FVM is manifested, where also, as in the finite element method, it is possible to represent a region with round borders through splitting into triangles or any other polygons. But FVM has another 1 plus - when going from triangles to polygons with a large number of sides absolutely nothing is required, of course, if the code was written for an arbitrary triangle and not an equilateral one. Moreover, without changing the code, you can use a mixture of different elements - triangles, polygons, squares, and so on.
Consider the general case when the vector connecting the centers of 2 elements does not coincide with the vector of the normal to the common face of these elements. The flux calculation through the edge will now consist of 2 parts. In the first, the orthogonal component will be calculated and in the second, the so-called “cross” -diffusion".
The picture shows 2 elements, C is the current element under consideration and F is the neighboring element. Let us describe the discretization for the face separating these 2 elements. The vector connecting the centers of the elements is DCF. Vector e is the unit vector in the direction of DCF. Vector Sf is directed along the normal to the face, its length is equal to the length of the face.

The calculation scheme looks like this.

The second term here is cross-diffusion, it will be the greater, the greater the difference between the vectors Ef and Sf, if they coincide, then it is equal to 0.
We first write out the orthogonal part (minimum correction method).

In the source, I did not implement the term with cross-diffusion, because the question arose - how to check the correctness of such a implementation. Visually, the comparison of Matlab's and mine’s results was no different in the absence of cross-diffusion. which ultimately makes crossdiffusion = 0. Perhaps later I will return to this issue.
The calculation of boundary elements is no different from the calculations not at the border, instead of the center of the neighboring element is taken the center of the face, well, and as usual the temperature at the border is substituted.
In my implementation, the result is:
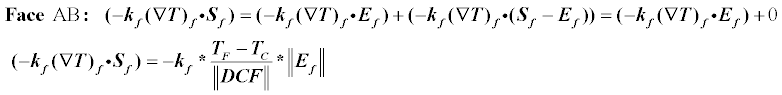
The test was conducted by comparing the results in Matlab and my implementation. Mesh was used the same, was unloaded from Matlab and loaded into the program. For some triangle artifacts do not pay attention, this is just an incomprehensible rendering glitch.

GitHab source is here
The main version in the heat2PolyV2 folder. What applies to the computing part lies in heat2PolyV2 \ Src \ FiniteVolume \.
At the beginning of the file Scene2.cs are the parameters that can be changed for display in different color schemes, scale, mesh display, etc. The examples themselves are stored in heat2PolyV2 \ bin \ Debug \ Demos \
Unloading from Matlab is simple - you need to open the pde toolbox, open the m file (or create it yourself from scratch), go to the Mesh-Export mesh menu, click OK; go to the main Matlab, variables will appear in the panel - mat of the pet, open the savemymesh.m file, execute it, the p.out file will appear, transfer it to the Demos folder.
In the source code to select an example, you must specify the file name in the line param.file = "p"; (FormParam.cs). Next you need to apply boundary conditions - for ready-made examples, you can simply uncomment the corresponding blocks in MainSolver.cs:
The meaning here is simple - Matlab divides the boundaries by domain, for example, external and internal. Also, for each domain, the boundaries are divided into parts (groups) so that conditions can be set on sections of the border separately - for example, right or bottom.
It is possible not to use Matlab at all, but to manually register all elements (triangles) and their vertices + faces (only for boundary elements)

Finite Volume (FVM) method
The method is based on dividing the region into non-intersecting control volumes (elements), the nodal points where a solution is sought. Solving it - we find the values.
desired variables at nodal points. For a single element, the equation is obtained by integrating the original diff of the equation with respect to the element and approximating the integrals.
The term final volume in the article will often be replaced with the Element, for convenience we will consider them equivalent (the element in this article has nothing to do with the finite element method).
')
There are 2 different ways to solve the FVM problem:
1) the faces of the control volume coincide with the faces of the element
2) the faces of the control volume pass through the centers of the faces of the elements (into which the region is divided). The desired variables are stored at the vertices of these elements. A control volume is built around each vertex. For a non-rectangular grid, this method has 2 more subspecies.

We will use method 1) with control volumes coinciding with the elements into which the region is divided.
Some advantages of FVM:
- preservation of basic quantities throughout the region, such as system energy, mass, heat fluxes, and so on. This condition is fulfilled even for a rough computational grid
- high speed of calculation. Many calculated values can be calculated when a region is divided into elements, and it is not necessary to calculate them at each time step.
- ease of use for tasks with complex geometry and curvilinear borders. The ease of using different geometric types of elements - triangles, polygons.
The FVM method is implemented on the example of the heat equation:
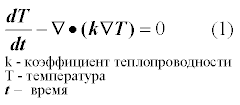
So the main steps in the implementation of FVM:
- Translation diff equations into a form suitable for FVM - integration over the control volume
- Drawing up a discrete analogue, choosing a method for converting derivatives and other integrands into discrete form
- Obtaining an equation for each of the control volumes into which the region is divided. Compilation of a system of linear equations and its solution.
Time discretization.
For the time derivative, we use the standard simplest method of Euler. This will be an explicit time scheme, where the sought from the previous step are taken. And at the first step, we set the initial conditions.

A bit of theory or the first step in the implementation of FVM
Using the divergence theorem, the integral of volume is transformed into an integral of area. The meaning is that we replace integration over the entire internal volume of our element with integration only over the surface of this volume. This formulation is more suitable for the 3D case. For 2D, instead of volume V - the area of the element, and instead of S - the perimeter of the element. It turns out that the integral over the area is replaced by an integral along the perimeter. In fact, the degree of derivative decreases. If, for example, there is a second derivative, then only ervaya, when was the first - instead of the derivative will be sought peremennaya.Nado just have to remember that we are dealing not with the usual derivative with a divergence.
So the second term in our equation after integration is transformed as follows:
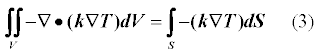
FVM on a standard rectangular grid

The figure shows Element C and its neighboring elements on the right (E), on the left (W), on the top (N) and on the bottom (S) . The element C has 4 faces marked with letters ewns . It is these 4 faces that make up the perimeter of the element and integration is performed. For each element, as a result, we obtain a discrete analog of the original diff equation.
Let us make a discrete analogue for element C. To begin, we need to understand the integral (3). The integral is in fact a sum. Therefore, we replace the integral over the entire surface of the element by the sum of the 4 components of this surface, ie 4 edges of the element.
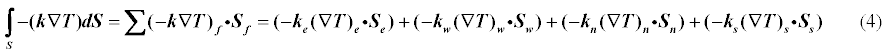
The ewns indices here mean that the expression or variable is calculated in the center of the corresponding face.
Now let's put together the resulting simplifications of the parts of the original diff equation - terms (2) and (4). We get the first approximation level:

Now we only need to approximate (4) until the end, since the gradient enters there, and we need to convert it into numerical form. In fact, this sum represents the sum of heat fluxes through the edges. Our case is simplified for a rectangular grid, because the normal to the face only 1 component remains - either along the x axis or along y.
Let us analyze this process in detail using the example of the e face.

Now we substitute instead of the sum in the equation (5) the obtained discrete analogs for 4 faces:
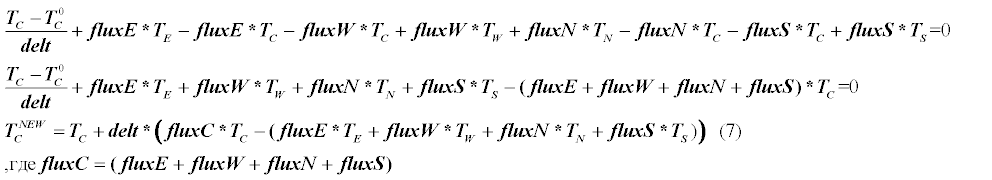
Equation (7) is the final equation for the element C, from which we obtain at each time step a new value of temperature (Tnew) in the element C.
Boundary conditions on a rectangular grid
The figure shows the element C whose face e is at the boundary and the temperature values on this face are known, either as a given temperature or as a given heat flux through the face.

We consider only 2 types of boundary conditions.
- Tb temperature set at border
- FluxB flow is set on the border, we consider only the case when FluxB = 0, i.e. face e will be insulated
Case 2) is the simplest, since it turns out that the e face is not required at discretization (since all the coefficients are Flux = 0) and you can simply skip it.
Now consider case 1). Discretization of the edge e will be generally similar to the one that has already been described. There will be only 2 changes - instead of Te there will be a known boundary value Tb and instead of a distance DXe it will be DXe / 2. Otherwise, you can consider the value Te as if this would be an ordinary neighboring node E. Now we shall write out the term for the boundary element C in more detail.
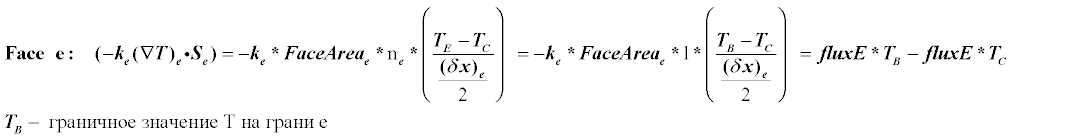
An example of numerical calculations on a rectangular grid
As an example, consider the area divided into 9 elements, grid 3 * 3. On the first slides, the following boundary conditions are applied: T = 0 on 3 sides, T = 240 set to the bottom. On the second slide line, on the sides, the boundary conditions with Flux are set. = 0, above T = 0, below T = 240. In each case there are 2 pictures, one with a breakdown of the area 3 * 3 elements, the second 40 * 40.
Calculation code for both cases (in the source is called heat2dminimum)
public void RunPhysic() { double Tc, Te, Tw, Tn, Ts; double FluxC, FluxE, FluxW, FluxN, FluxS; double dx = 0; double Tb = 240; double Tb0 = 0; int i, j; for (i = 0; i < imax; i++) for (j = 0; j < jmax; j++) { Tc = T[i, j]; dx = dh; if (i == imax - 1) { Te = Tb0; dx = dx / 2; } else Te = T[i + 1, j]; FluxE = (-k * FaceArea) / dx; if (i == 0) { Tw = Tb0; dx = dx / 2; } else Tw = T[i - 1, j]; FluxW = (-k * FaceArea) / dx; if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; } else Tn = T[i, j + 1]; FluxN = (-k * FaceArea) / dx; if (j == 0) { Ts = Tb; dx = dx / 2; } else Ts = T[i, j - 1]; FluxS = (-k * FaceArea) / dx; FluxC = FluxE + FluxW + FluxN + FluxS; T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts)); } } //Insulated public void RunPhysic2() { double Tc, Te, Tw, Tn, Ts; double FluxC, FluxE, FluxW, FluxN, FluxS; double dx = 0; double Tb = 240; double Tb0 = 0; int i, j; for (i = 0; i < imax; i++) for (j = 0; j < jmax; j++) { Tc = T[i, j]; dx = dh; Te = 0; Tw = 0; if (i == imax - 1) FluxE = 0; else { Te = T[i + 1, j]; FluxE = (-k * FaceArea) / dx; } if (i == 0) FluxW = 0; else { Tw = T[i - 1, j]; FluxW = (-k * FaceArea) / dx; } if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; } else Tn = T[i, j + 1]; FluxN = (-k * FaceArea) / dx; if (j == 0) { Ts = Tb; dx = dx / 2; } else Ts = T[i, j - 1]; FluxS = (-k * FaceArea) / dx; FluxC = FluxE + FluxW + FluxN + FluxS; T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts)); } } 
FVM in problems with complex geometry
This is where the advantage of FVM is manifested, where also, as in the finite element method, it is possible to represent a region with round borders through splitting into triangles or any other polygons. But FVM has another 1 plus - when going from triangles to polygons with a large number of sides absolutely nothing is required, of course, if the code was written for an arbitrary triangle and not an equilateral one. Moreover, without changing the code, you can use a mixture of different elements - triangles, polygons, squares, and so on.
Consider the general case when the vector connecting the centers of 2 elements does not coincide with the vector of the normal to the common face of these elements. The flux calculation through the edge will now consist of 2 parts. In the first, the orthogonal component will be calculated and in the second, the so-called “cross” -diffusion".
The picture shows 2 elements, C is the current element under consideration and F is the neighboring element. Let us describe the discretization for the face separating these 2 elements. The vector connecting the centers of the elements is DCF. Vector e is the unit vector in the direction of DCF. Vector Sf is directed along the normal to the face, its length is equal to the length of the face.

The calculation scheme looks like this.

The second term here is cross-diffusion, it will be the greater, the greater the difference between the vectors Ef and Sf, if they coincide, then it is equal to 0.
We first write out the orthogonal part (minimum correction method).

In the source, I did not implement the term with cross-diffusion, because the question arose - how to check the correctness of such a implementation. Visually, the comparison of Matlab's and mine’s results was no different in the absence of cross-diffusion. which ultimately makes crossdiffusion = 0. Perhaps later I will return to this issue.
The calculation of boundary elements is no different from the calculations not at the border, instead of the center of the neighboring element is taken the center of the face, well, and as usual the temperature at the border is substituted.
In my implementation, the result is:
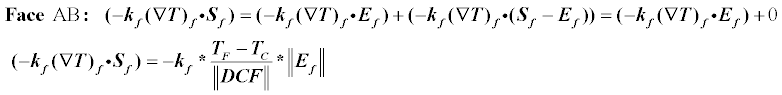
Calculation code for an arbitrary polygon (in the source is called heat2PolyTeach)
public void Calc() { double bc, ac; double sumflux; double[] aa = new double[6]; double[] bb = new double[6]; int e; for (e = 0; e < elementcount; e++) { Element elem = elements[e]; int nf; bc = 0; ac = 0; sumflux = 0; for (int nn = 0; nn <6; nn++) { aa[nn] = 0; bb[nn] = 0; } for (nf = 0; nf < elem.vertex.Length; nf++) { Face face = elem.faces[nf]; Element nb = elem.nbs[nf]; if (face.isboundary) { if (face.boundaryType == BoundaryType.BND_CONST) { double flux1; double flux; flux1 = elem.k * (face.area / elem.nodedistances[nf]); Vector2 Sf = face.sf.Clone(); Vector2 dCf = elem.cfdistance[nf].Clone(); if (Sf * dCf < 0) Sf = -Sf; //1) minimum correction //Vector2 DCF = elem.cndistance[nf].Clone(); Vector2 e1 = dCf.GetNormalize(); Vector2 EF = (e1 * Sf) * e1; flux = elem.k * (EF.Length() / dCf.Length()); ac += flux; bc += flux * face.bndu; bb[nf] = flux; } else if (face.boundaryType == BoundaryType.BND_INSULATED) { double flux; flux = 0; ac += flux; bc += flux * face.bndu; bb[nf] = flux; } } else { double flux1; double flux; flux1 = -elem.k * (face.area / elem.nodedistances[nf]); Vector2 Sf = face.sf.Clone(); Vector2 dCf = elem.cfdistance[nf].Clone(); if (Sf * dCf < 0) Sf = -Sf; Vector2 DCF = elem.cndistance[nf].Clone(); Vector2 e1 = DCF.GetNormalize(); //corrected flux //1) minimum correction Vector2 EF = (e1 * Sf) * e1; flux = -elem.k * (EF.Length() / DCF.Length()); sumflux += flux * nb.u; ac += -flux; aa[nf] = -flux; } } elem.u = elem.u + delt * (bc - sumflux - ac * elem.u); } } Examples and verification of results
The test was conducted by comparing the results in Matlab and my implementation. Mesh was used the same, was unloaded from Matlab and loaded into the program. For some triangle artifacts do not pay attention, this is just an incomprehensible rendering glitch.

Description of the source structure
GitHab source is here
The main version in the heat2PolyV2 folder. What applies to the computing part lies in heat2PolyV2 \ Src \ FiniteVolume \.
At the beginning of the file Scene2.cs are the parameters that can be changed for display in different color schemes, scale, mesh display, etc. The examples themselves are stored in heat2PolyV2 \ bin \ Debug \ Demos \
Unloading from Matlab is simple - you need to open the pde toolbox, open the m file (or create it yourself from scratch), go to the Mesh-Export mesh menu, click OK; go to the main Matlab, variables will appear in the panel - mat of the pet, open the savemymesh.m file, execute it, the p.out file will appear, transfer it to the Demos folder.
In the source code to select an example, you must specify the file name in the line param.file = "p"; (FormParam.cs). Next you need to apply boundary conditions - for ready-made examples, you can simply uncomment the corresponding blocks in MainSolver.cs:
//p.out public void SetPeriodicBoundary() The meaning here is simple - Matlab divides the boundaries by domain, for example, external and internal. Also, for each domain, the boundaries are divided into parts (groups) so that conditions can be set on sections of the border separately - for example, right or bottom.
It is possible not to use Matlab at all, but to manually register all elements (triangles) and their vertices + faces (only for boundary elements)
Description of the structure of the .out file
The file is divided into sections - ## Points (vertices), ## Triangle (triangles) and ## Boundary (faces - only those that are on the border)
## Points - coordinates of points, the first line is x, the second is y.
## Triangle - triangles, the first line is the index of the 1st vertex in the ## Points array, 2 and 3 lines are the indices 2 and 3 of the triangle top.
## Boundary is the faces, the first line is the index of the 1st vertex of the face, the 2nd is the index of the second vertex, the fifth line is the group, the sixth is the domain
## Points - coordinates of points, the first line is x, the second is y.
## Triangle - triangles, the first line is the index of the 1st vertex in the ## Points array, 2 and 3 lines are the indices 2 and 3 of the triangle top.
## Boundary is the faces, the first line is the index of the 1st vertex of the face, the 2nd is the index of the second vertex, the fifth line is the group, the sixth is the domain
Description of source folders
Sources are written in Visual Studio 2010 c #. Used by Matlab R2012a.
Source code github
Source code github
- heat2PolyV2 - final version
- other \ heat2Utrianglestatic - implemented an example from the book p346 versteeg_h malalasekra_w_ An_introduction_to_computational_fluid ...
- other \ water2dV2 - an attempt to solve the Navier-Stokes equations in part using FiniteVolume
- matlab - m files of examples pde toolbox + savemymesh.m which unloads a ready .out file for heat2PolyV2
List of books on the subject
- The finite volume method - there is already a second edition
- F.Moukalled L.Mangani M.Darwish The finite volume method of computational fluid dynamics 2016 - released recently (almost yesterday :)
- Patankar S.-Numerical methods for solving problems of heat transfer and fluid dynamics-Energoatomizdat (1984)
- Patankar S.V.-Numerical solution of problems of heat conduction and convective heat exchange during flow in channels MEI (2003)
- Ferziger JH Peric 2001 Computational Methods for Fluid Dynamics - although not directly related to FVM, but very useful
Source: https://habr.com/ru/post/276193/
All Articles