Fuzzy search in the dictionary with the universal Levenshtein automaton. Part 2

In the first part of the article, we considered the Levenshtein universal automaton - a powerful tool for filtering words that are separated from a certain word W by a Levenshtein distance of no more than a given one. Now it's time to learn how to use this tool to effectively solve the fuzzy search problem in the dictionary.

')
The simplest and most obvious algorithm for solving a fuzzy search problem in a dictionary using a Levenshtein automaton is a brute force algorithm. In this case, for each word in the dictionary, the Levenshtein distance (Damerau-Levenshtein) is estimated to the search query. An example implementation in C # can be seen in the first part of the article .

The use of even this simple algorithm gives a performance gain compared with the use of dynamic programming methods. However, there are more efficient algorithms.

Schultz and Mihov basic algorithm

Consider the first such algorithm - as far as I know, it was proposed by Schulz and Mikhov (2002) , so I will call it the basic algorithm of Schulz and Mihov, or simply the basic algorithm . So, let for the allegedly distorted word W and the threshold value of the editing distance N, a deterministic Lowenstein automaton A _N (W) is given . Let the considered dictionary D also be represented in the form of a deterministic finite automaton A _D having the input alphabet E. The states of automata will be denoted as q and q ^D, respectively, the transition functions as V and V ^D , and the set of final states as F and F ^D. The algorithm of fuzzy search in the dictionary proposed by Schulz and Mikhov is a standard search procedure with a return and can be described by the following pseudo-code:

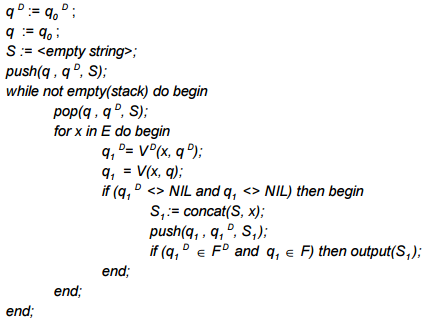
The algorithm starts with the initial states of automata. As new characters are fed into the input, subsequent states are placed on the stack if they are not empty. If the successive states of both automata are finite, the search word is found.

This algorithm can still be imagined as the "intersection" of finite automata. Only those words that correspond to the final states of both automata fall into the resulting sample. In this case, only those prefixes that translate both automata into a non-empty state are considered.

The computational complexity of the algorithm depends on the size of the dictionary and the editing distance N. If N reaches the size of the longest word in the dictionary, then the algorithm reduces to a complete search of the states of the automaton A _D. But when solving practical problems, as a rule, small values of N are used . In this case, the algorithm considers only a very small subset of the states of the automaton A _D. When N = 0, the algorithm finds the word W in the dictionary over time O (| W |) .

It should be noted that the described algorithm ensures the absence of losses during the search. That is, 100% of words in the dictionary, separated from W by a distance of not more than N, will be included in the resulting sample.

Features of software implementation

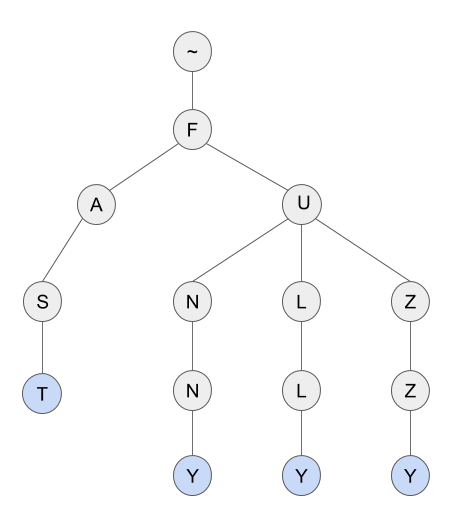
I guess you are already familiar with such a data structure as a prefix tree . The prefix tree is also known as “loaded tree” (or “bor”, “ray”, “Trie”) and is successfully used to store dictionaries. The figure shows a prefix tree for a dictionary of four words: “fast”, “funny”, “fully”, “fuzzy”.

If you are not familiar with the prefix tree, then you can familiarize yourself with the publications in which this structure is considered in detail, for example, here .

Why do I want to use a prefix tree for dictionary storage? Because the prefix tree can be considered as a finite state machine. Each tree node represents the state of the automaton. The initial state is the root of the tree, and the final states are the nodes corresponding to the words. For each node and symbol only one transition is possible - the automaton is deterministic.

So, considering the prefix tree as a deterministic finite automaton and having the software implementation of the deterministic Levenshtein automaton, it is easy to turn the pseudo-code of the algorithm into code in any programming language. Under the spoiler example in C #.

Basic algorithm

/// <summary> /// Find all words in dictionary such that Levenstein distance to typo less or equal to editDistance /// </summary> /// <returns>Set of possible corrections</returns> /// <param name="typo">Garbled word.</param> /// <param name="dictionary">Dictionary.</param> /// <param name="editDistance">Edit distance.</param> IEnumerable<string> GetCorrections(string typo, TrieNode dictionary, int editDistance) { var corrections = new List<string> (); if (string.IsNullOrEmpty (typo.Trim())) { return corrections; } //Create automaton LevTAutomataImitation automaton = new LevTAutomataImitation (typo, editDistance); //Init stack with start states Stack<TypoCorrectorState> stack = new Stack<TypoCorrectorState> (); stack.Push (new TypoCorrectorState () { Node = dictionary, AutomataState = 0, AutomataOffset = 0, }); //Traversing trie with standart backtracking procedure while (stack.Count > 0) { //State to process TypoCorrectorState state = stack.Pop(); automaton.LoadState (state.AutomataState, state.AutomataOffset); //Iterate over TrieNode children foreach (char c in state.Node.children.Keys) { //Evaluate state of Levenstein automaton for given letter int vector = automaton.GetCharacteristicVector (c, state.AutomataOffset); AutomataState nextState = automaton.GetNextState (vector); //If next state is not empty state if (nextState != null) { TrieNode nextNode = state.Node.children [c]; //Push node and automaton state to the stack stack.Push (new TypoCorrectorState () { Node = nextNode, AutomataState = nextState.State, AutomataOffset = nextState.Offset }); //Check if word with Levenstein distance <= n found if (nextNode.IsWord && automaton.IsAcceptState (nextState.State, nextState.Offset)) { corrections.Add (nextNode.Value); } } } } return corrections; }

FB-Trie Algorithm

Go ahead. In 2004, Mihov and Schulz proposed a modification of the above algorithm, the main idea of which is to use a direct and inverse prefix tree in combination with splitting the search query W into two approximately equal parts W ₁ and W ₂ . The algorithm is known as FB-Trie (from forward and backward trie).

Under the inverse prefix tree, you should understand the prefix tree constructed from the inversions of all vocabulary words. Inversion of a word, I call simply a word written backwards.

An important point - in their work, Mihov and Schulz showed that the Damerau-Levenshtein distance between inversions of two rows is equal to the distance between the rows themselves.

The operation of the algorithm for N = 1 is based on the following statement: any string S that is separated from the string W at Damerau-Levenshtein distance d (S, W) <= 1 can be divided into two parts S ₁ and S ₂ only in such a way that one of three mutually exclusive conditions:

a) d (S ₁ , W ₁ ) = 0 and d (S ₂ , W ₂ ) <= 1

b) d (S ₁ , W ₁ ) <= 1 and d (S ₂ , W ₂ ) = 0

c) d (S ₁ , W ₁ ') = 0 and d (S ₂ , W ₂ ') = 0

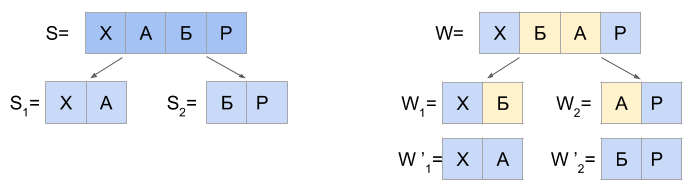
In paragraph “c”, the strings W ₁ ' and W ₂ ' are obtained from the strings W ₁ and W ₂ by replacing the last character W ₁ with the first character W ₂ and vice versa. For example, if W ₁ = 'FU', and W ₂ = 'ZZY', then W ₁ ' =' FZ ', and W ₂ ' = 'UZY'.

How can you quickly find in the dictionary all the words that fit the variant “a”? Very simple: find a node in the prefix tree with the prefix W ₁ , then bypass all its successors in accordance with the basic algorithm of Schulz and Mihov and select those whose keys are no more than 1 from W ₂ .

Option A

 //May be for some S d(S1, W1) = 0 and d(S2, W2) <= 1? TrieNode lnode = ForwardDictionary.GetNode (left); if (lnode != null) { corrections.AddRange(GetCorrections(right, lnode, 1)); }

For option “b”, the inverse prefix tree is useful: find the node in it corresponding to the inverted string W ₂ , then go around all its heirs and select those whose keys are separated from the inverted W ₁ by no more than 1 - again, in accordance with the basic algorithm .

Option B

 //May be for some S d(S1, W1) = 1 and d(S2, W2) = 0? TrieNode rnode = BackwardDictionary.GetNode (rright); if (rnode != null) { corrections.AddRange(GetCorrections(rleft, rnode, 1)))); }

For the “in” variant, it is necessary to simply swap two characters in the word W on the boundary of the partition and check whether the received word is contained in the prefix tree.

Option B

 //May be there is a transposition in the middle? char[] temp = typo.ToCharArray (); char c = temp [llen - 1]; temp [llen - 1] = temp [llen]; temp [llen] = c; TrieNode n = ForwardDictionary.GetWord (new string(temp)); if (n != null) { corrections.Add (n.Key); }

To solve the fuzzy search problem in the dictionary using the FB-Trie algorithm, you just need to find the three sets of words listed above and combine them.

For N = 2, two more cases will need to be considered:

a) d (S ₁ , W ₁ ) = 0 and d (S ₂ , W ₂ ) <= 2

b) 1 <= d (S ₁ , W ₁ ) <= 2 and d (S ₂ , W ₂ ) = 0

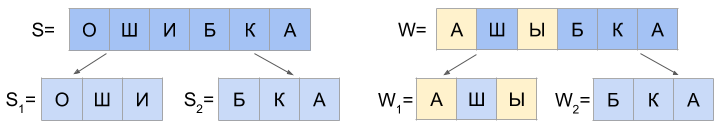
c) d (S ₁ , W ₁ ) = 1 and d (S ₂ , W ₂ ) = 1

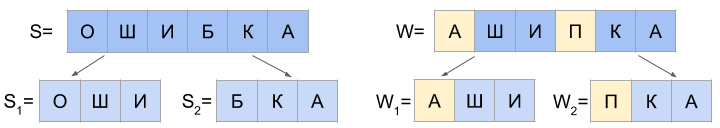
And if the last character of the string S ₁ is equal to the first character W ₂ , and the last character W ₁ is equal to the first character S ₂ , then two more cases are possible:

d) d (S ₁ , W ₁ ') = 0 and d (S ₂ , W ₂ ') <= 1

d) d (S ₁ , W ₁ ') <= 1 and d (S ₂ , W ₂ ') = 0

The first two cases are easily detected by analogy with the options “a” and “b” for N = 1, but the Levenshtein machine is used for N = 2.

The options “d” and “d” for N = 2 repeat the options “a” and “b” for N = 1, except that instead of substrings W ₁ and W ₂ , W ₁ ' and W ₁ ' are used .

The “in” option is a bit more complicated. In the first step, it is necessary to find in the direct prefix tree all the nodes corresponding to the prefixes that are no more than 1 from W 1 (basic algorithm). In the second step, for each such node, it is necessary to bypass the children and select those that correspond to the keys that are no more than 1 from W ₂ (again, the basic algorithm).

For N = 3, seven cases will need to be considered. I will not bring them here - you can see in the original article by Mihov and Schultz (2004) . By analogy, one can continue for arbitrary N , although the need for this in solving practical problems is unlikely to arise.

Performance scores

Curiously, the search time using the FB-Trie algorithm decreases as the word length W increases.

A detailed analysis of the search time using the FB-Trie algorithm in comparison with other well-known fuzzy search algorithms can be found in Leonid Boytsov’s “Indexing Methods for Approximate Dictionary Searching: Comparative Analysis” (2011) . In this paper, a thorough comparison of the search time and the amount of memory consumed for such algorithms as:

brute force;
various modifications of the n-gram method;
various modifications of the sample extension method;
signature hashing;
FB-Trie and other algorithms.

I will not repeat here all the numerous figures and graphs, but I will confine myself to general conclusions for natural languages.

So, the FB-Trie algorithm provides a reasonable compromise between performance and memory consumption. If your application needs to maintain an editing distance of 2 or more, and the dictionary contains more than 500,000 words, the FB-Trie algorithm is a rational choice. It will provide the minimum search time at a reasonable memory consumption (about 300% of the memory occupied by the lexicon).

If you decide to limit yourself to the N = 1 editing distance, or you have a small dictionary, then a number of algorithms may work faster (for example, the Mor − Fraenkel method or FastSS ), however, be prepared for increased memory consumption (up to 20,000% of the lexicon size). If you have dozens of gigabytes of RAM to store a fuzzy index, you can use these methods for large dictionary sizes.

So that the reader can decide how much it is - 500,000 words, I will give some figures on the number of words in the Russian language (taken from here ).

Lopatin's spelling dictionary contains 162,240 words - the lexicon file size is 2 MB.
The list of Russian surnames includes at least 247,780 surnames - the lexicon file size is 4.6 MB.
The complete accentuated paradigm of the Russian language according to A. A. Zaliznyak is 2,645,347 word forms, the size of the lexicon file is about 35MB.

And what if you do not have the ability to store the dictionary in the form of two prefix trees? For example, it is presented in the form of a sorted list. In this case, the use of a Levenshtein automaton for a fuzzy search is possible, but impractical. Perhaps - because there are various modifications of complete enumeration (for example, with clipping along the length of the word | W | plus minus N ). It is impractical - because you will not get a performance gain compared to more simple-to-implement methods (for example, the sample extension algorithm ).

I note that the basic algorithm of Schulz and Mihov requires two times less memory than the FB-Trie algorithm. However, you will have to pay an increase in the search time by an order of magnitude (estimation of the authors of the algorithm).

On this consideration of fuzzy search algorithms in the dictionary using a Levenshtein automaton is considered complete.

Yes, full C # Spellchecker source code can be found here . Probably, my implementation is not optimal in terms of performance, but it will help you understand the operation of the FB-Trie algorithm and may be useful in solving your applied problems.

Everyone who read the publication - many thanks for your interest.

Fuzzy search in the dictionary with the universal Levenshtein automaton. Part 2

Schultz and Mihov basic algorithm

Features of software implementation

FB-Trie Algorithm

Performance scores

Links

More articles: