Sandelius method for random permutations
Articles about obtaining (pseudo) random numbers, about checking the quality of the obtained sequences invariably arouse the interest of the Habr population.
However, in applications, along with sequences of random and pseudo-random numbers, it is required to obtain permutations of numbers having a uniform distribution . For example, the need for such permutations periodically appears in cryptographic applications.
The method described below was proposed by Sandelius (M. Sandelius) as early as 1962 in [1].
')
The described algorithm allows to obtain random permutations of n elements that have a uniform distribution . The latter means that the probability of getting one of n! possible substitutions using this method is 1 / n! ..
Sandelius method is easier to describe recursively.
At each step, array P is processed. For array P, random bits are generated in an amount equal to the number of elements in array P. The i-th bit of the sequence is mapped to the i-element of array P. Array P is divided into two arrays P0 and P1 by the principle: all elements which are mapped zeros are entered into the array P0, the rest in the array P1. Mixing (recursion) is performed for each array P0 and P1. Mixed arrays are combined into one. First come the elements from the array P0, then from the array P1.
Sandelius Mixing Procedure (P):
The algorithm is fairly easy to program.
Hopefully, the algorithm for generating permutations is described by me quite clearly. Now I want to discuss a little, especially his work.
To work, the algorithm requires a sequence of random bits. The main requirement for this sequence is that the bits must be independent . In this case, the algorithm generates evenly distributed permutations even.
It should be borne in mind that random bits may have an uneven distribution, but they must be independent , otherwise the distribution of substitutions will not be uniform.
The disadvantages include the fact that the number of random bits that are required to generate a permutation is not defined in advance.
I must say at once that the facts mentioned in the previous paragraph are proved analytically, but I still wanted to check them in practice.
To check the uniformity of distribution of the obtained substitutions, a simple program is written in the mathematical package Maple. In the program, I generated a large number of permutations, counted the number of substitutions of each type (something like a histogram). For the resulting array, we tested the hypothesis of uniformity by the Pearson criterion. In addition, the distribution of the number of bits required to generate a single substitution was calculated.
I don’t see any reason to give the source code of the program here, but if there is a desire to calculate it myself, then the files with source codes can be found here .
Permutations of length n = 7 were investigated. N = n! * 1000 permutations were generated. Random bits were generated as follows: 0 with a probability of 0.5 + d, 1 with a probability of 0.5-d. d is 0 for evenly distributed bits. To obtain the dependent bit, a random bit was generated and added to the previous bit.
The number n = 7 is taken from considerations of reasonable execution time (I have 10-20 minutes).
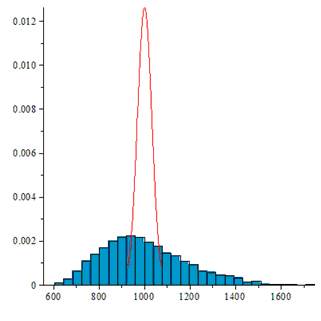
In the figures horizontally marked numbers of permutations, and the vertical frequency of their appearance. With the naked eye it can be seen that in the latter case the distribution is very different from the uniform one.
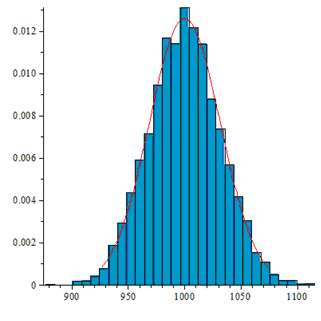
It is also seen that, regardless of the bias in the probability of independent random bits, the algorithm generates uniformly distributed permutations. However, the greater the bias in probability, the more random bits the algorithm requires.
If the bits have a dependency, then the generated substitutions have a distribution different from the uniform distribution.
The number of substitutions of each type must have a distribution close to normal with average N / n! and the variance N / n! (1-1 / n!).
In the first three cases, the histogram looks like this:
In the latter case, the distribution is far from the expected:
1. M. Sandelius. A Simple Randomization Procedure, J. of the Royal Statistical Society. Ser. V., V. 24, No. 2, 1962.
However, in applications, along with sequences of random and pseudo-random numbers, it is required to obtain permutations of numbers having a uniform distribution . For example, the need for such permutations periodically appears in cryptographic applications.
The method described below was proposed by Sandelius (M. Sandelius) as early as 1962 in [1].
')
The described algorithm allows to obtain random permutations of n elements that have a uniform distribution . The latter means that the probability of getting one of n! possible substitutions using this method is 1 / n! ..
Algorithm for obtaining permutations
Sandelius method is easier to describe recursively.
At each step, array P is processed. For array P, random bits are generated in an amount equal to the number of elements in array P. The i-th bit of the sequence is mapped to the i-element of array P. Array P is divided into two arrays P0 and P1 by the principle: all elements which are mapped zeros are entered into the array P0, the rest in the array P1. Mixing (recursion) is performed for each array P0 and P1. Mixed arrays are combined into one. First come the elements from the array P0, then from the array P1.
Sandelius Mixing Procedure (P):
1. n := |P|; - ( ) P 2. n=1, P; 3. g:=[gi, i=1..n]; – gi 4. P0:=[]; P1:=[]; - 5. i0:=0; i1:=0; - 6. k:= 0; 7. g[k]=0, 7.1. P0[i0] := P[k]; 7.2. i0 := i0+1; 8. g[k]=1, 8.1. P1[i1] := P[k]; 8.2. i1 := i1+1; 9. k := k+1; 10. k<n, 7. 11. P0 := Sandelius(P0); 12. P1 := Sandelius(P1); 13. P := P0||P1 – . 14. P. 1 n: P=[1,2, …,n]; Sandelius(P); The algorithm is fairly easy to program.
So, for example, you can program in Maple
Sandelius:=proc(p) local A,m,i,p1,p2; m:=nops(p); A:=[seq(getNextRndBit(), i=1..m)]; p1:=[]; p2:=[]; for i from 1 to m do if A[i]=0 then p1:=[op(p1),p[i]]; else p2:=[op(p2),p[i]]; fi; od; if nops(p1)>1 then p1:=Sandelius(p1); fi; if nops(p2)>1 then p2:=Sandelius(p2); fi; return [op(p1),op(p2)]; end proc: Here is an example of my implementation of the algorithm in C ++, which I used in one of my studies
unsigned __int8 *bits,*tmp_perm; Sandelius(unsigned __int8 *perm,int n) { tmp_perm = (unsigned __int8 *)malloc(n); bits = (unsigned __int8 *)malloc(n); for(int i=0;i<n;i++) perm[i]=i; recursiveSandelius(perm,n); free(bits); free(tmp_perm); } recursiveSandelius(unsigned __int8 *perm,int n) { if (n<=1) return; for(int i=0;i<n;i++) bits[i]=getNextRndBit(); k=0; for(int i=0;i<n;i++) if(!bits[i]) tmp_perm[k++]=perm[i]; zeros=k; for(int i=0;i<n;i++) if(bits[i]) tmp_perm[k++]=perm[i]; memcpy(perm,tmp_perm,n); recursiveSandelius (perm,zeros); recursiveSandelius (&perm[zeros],n-zeros); } Special features
Hopefully, the algorithm for generating permutations is described by me quite clearly. Now I want to discuss a little, especially his work.
To work, the algorithm requires a sequence of random bits. The main requirement for this sequence is that the bits must be independent . In this case, the algorithm generates evenly distributed permutations even.
It should be borne in mind that random bits may have an uneven distribution, but they must be independent , otherwise the distribution of substitutions will not be uniform.
The disadvantages include the fact that the number of random bits that are required to generate a permutation is not defined in advance.
Practical check
I must say at once that the facts mentioned in the previous paragraph are proved analytically, but I still wanted to check them in practice.
To check the uniformity of distribution of the obtained substitutions, a simple program is written in the mathematical package Maple. In the program, I generated a large number of permutations, counted the number of substitutions of each type (something like a histogram). For the resulting array, we tested the hypothesis of uniformity by the Pearson criterion. In addition, the distribution of the number of bits required to generate a single substitution was calculated.
I don’t see any reason to give the source code of the program here, but if there is a desire to calculate it myself, then the files with source codes can be found here .
Permutations of length n = 7 were investigated. N = n! * 1000 permutations were generated. Random bits were generated as follows: 0 with a probability of 0.5 + d, 1 with a probability of 0.5-d. d is 0 for evenly distributed bits. To obtain the dependent bit, a random bit was generated and added to the previous bit.
The number n = 7 is taken from considerations of reasonable execution time (I have 10-20 minutes).
| Option | Equal probable substitutions (Pearson criterion)? | bar chart | Average number of random bits / standard deviation |
|---|---|---|---|
| Independent bits, d = 0 | Yes |  | 28.24 / 28.26 |
| Independent bits, d = 0.05 | Yes |  | 28.50 / 28,54 |
| Independent bits, d = 0.4 | Yes | 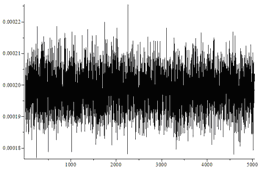 | 71.47 / 74.77 |
| Dependent bits, d = 0.05 | Not | 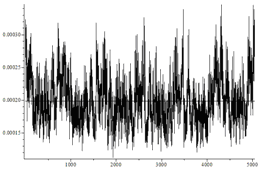 | 30.15 / 30.32 |
In the figures horizontally marked numbers of permutations, and the vertical frequency of their appearance. With the naked eye it can be seen that in the latter case the distribution is very different from the uniform one.
It is also seen that, regardless of the bias in the probability of independent random bits, the algorithm generates uniformly distributed permutations. However, the greater the bias in probability, the more random bits the algorithm requires.
If the bits have a dependency, then the generated substitutions have a distribution different from the uniform distribution.
The number of substitutions of each type must have a distribution close to normal with average N / n! and the variance N / n! (1-1 / n!).
In the first three cases, the histogram looks like this:

In the latter case, the distribution is far from the expected:

Literature
1. M. Sandelius. A Simple Randomization Procedure, J. of the Royal Statistical Society. Ser. V., V. 24, No. 2, 1962.
Source: https://habr.com/ru/post/275731/
All Articles