What should we build the Zhegalkin polynomial ...
I think everyone who has studied or is studying discrete mathematics at the university is familiar with the concept of the Zhegalkin polynomial .
The main feature of these polynomials is that any Boolean function can be represented by the Zhegalkin polynomial, and in a unique way.
Most often, for the construction of Zhegalkin polynomials, students are offered two methods for constructing such polynomials: the method of undetermined coefficients and the method of equivalent transformations.
')
Calculations using these methods are often cumbersome. By carelessness make a mistake is not difficult.
Under the cat, there is one convenient algorithm for constructing Zhegalkin polynomials, which students perceive with a bang, because It requires only the implementation of "mechanical actions" without the use of any mental effort. A brief description of the method can be found on Wikipedia, but in my opinion it is not entirely clear how to quickly perform calculations. To me, the method is known as the "Pascal triangle method."
The order of the calculations is easier to show by example. Next, I will step by step show how the calculation should look on paper (or how convenient it is to carry it out).
It is required to construct a Zhegalkin polynomial for the function f. For example, let's take the voting function as f%3Dx_1x_2%5Cvee%20x_2x_3%5Cvee%20x_1x_3%20%3D%20(00010111)) .
.
Step 1. We build a table of function values (the rows in the table go in ascending order of binary codes). The table is better placed on the left side of the sheet.

Step 2. Constructing a triangle.
To do this, take the vector of the function value and write it out opposite the first row of the table:

Next, fill in the triangle, adding in pairs the adjacent values modulo 2, the result of the addition is written below.

We continue the calculations until there is only one digit left in the line.
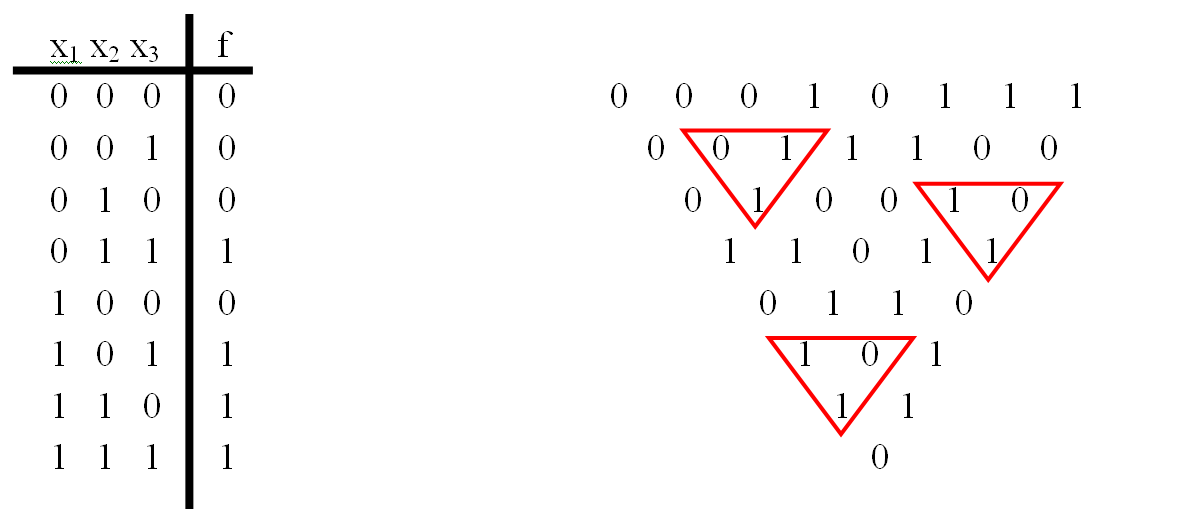
Step 3. Construction of the Zhegalkin polynomial.
We are interested in the left side of the triangle (values in bold):

The numbers on the left side (in bold) of the triangle are the coefficients of the polynomial with monotonous conjunctions corresponding to sets of variable values.
Now we write out for clarity, these conjunctions. We write conjunctions on binary sets in the left part of the table according to the following principle: if opposite to variable xi is 1, then the variable is included in the conjunction; otherwise, the variable is absent from the conjunction. The set (0,0,0) corresponds to the constant 1.

If the principle of obtaining conjunctions is clear, then a column with them can (even better) not be written out, but immediately proceed to the construction of a polynomial.
To construct a polynomial, we only need conjunctions from the rows with units on the left side of the triangle.
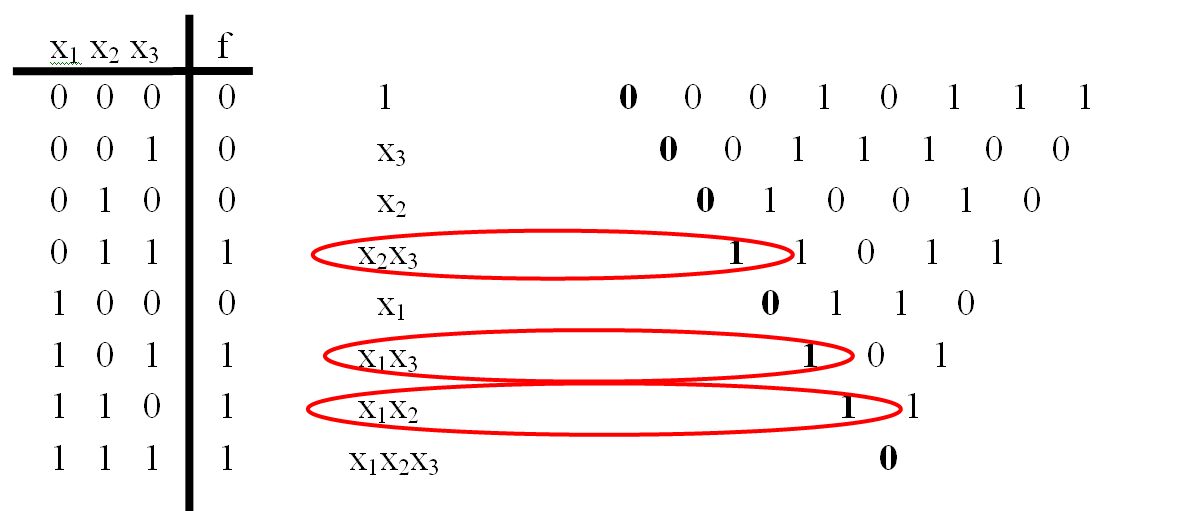
These are the conjunctions that make up the Zhegalkin polynomial. It remains only to write the polynom itself:
%3D%7B%7Bx%7D_%7B1%7D%7D%7B%7Bx%7D_%7B2%7D%7D%5Coplus%20%7B%7Bx%7D_%7B2%7D%7D%7B%7Bx%7D_%7B3%7D%7D%5Coplus%20%7B%7Bx%7D_%7B1%7D%7D%7B%7Bx%7D_%7B3%7D%7D.)
If the variables in the function are not 3, but 4 or more, then the method works unchanged, only the size of the tables will increase. However, in contrast to the method of uncertain coefficients, calculations can be performed without much effort on a sheet of paper.
Unfortunately, I was not able to find and see the source listed on Wikipedia:
V.P. Suprun Tabular method of polynomial decomposition of Boolean functions // Cybernetics. - 1987. - № 1. - p. 116-117.
The main feature of these polynomials is that any Boolean function can be represented by the Zhegalkin polynomial, and in a unique way.
Most often, for the construction of Zhegalkin polynomials, students are offered two methods for constructing such polynomials: the method of undetermined coefficients and the method of equivalent transformations.
')
Calculations using these methods are often cumbersome. By carelessness make a mistake is not difficult.
Under the cat, there is one convenient algorithm for constructing Zhegalkin polynomials, which students perceive with a bang, because It requires only the implementation of "mechanical actions" without the use of any mental effort. A brief description of the method can be found on Wikipedia, but in my opinion it is not entirely clear how to quickly perform calculations. To me, the method is known as the "Pascal triangle method."
The order of the calculations is easier to show by example. Next, I will step by step show how the calculation should look on paper (or how convenient it is to carry it out).
Pascal's triangle method
It is required to construct a Zhegalkin polynomial for the function f. For example, let's take the voting function as f
Step 1. We build a table of function values (the rows in the table go in ascending order of binary codes). The table is better placed on the left side of the sheet.

Step 2. Constructing a triangle.
To do this, take the vector of the function value and write it out opposite the first row of the table:

Next, fill in the triangle, adding in pairs the adjacent values modulo 2, the result of the addition is written below.

We continue the calculations until there is only one digit left in the line.

Step 3. Construction of the Zhegalkin polynomial.
We are interested in the left side of the triangle (values in bold):

The numbers on the left side (in bold) of the triangle are the coefficients of the polynomial with monotonous conjunctions corresponding to sets of variable values.
Now we write out for clarity, these conjunctions. We write conjunctions on binary sets in the left part of the table according to the following principle: if opposite to variable xi is 1, then the variable is included in the conjunction; otherwise, the variable is absent from the conjunction. The set (0,0,0) corresponds to the constant 1.

If the principle of obtaining conjunctions is clear, then a column with them can (even better) not be written out, but immediately proceed to the construction of a polynomial.
To construct a polynomial, we only need conjunctions from the rows with units on the left side of the triangle.

These are the conjunctions that make up the Zhegalkin polynomial. It remains only to write the polynom itself:
If the variables in the function are not 3, but 4 or more, then the method works unchanged, only the size of the tables will increase. However, in contrast to the method of uncertain coefficients, calculations can be performed without much effort on a sheet of paper.
Literature
Unfortunately, I was not able to find and see the source listed on Wikipedia:
V.P. Suprun Tabular method of polynomial decomposition of Boolean functions // Cybernetics. - 1987. - № 1. - p. 116-117.
Source: https://habr.com/ru/post/275527/
All Articles