How to reduce the number of measurements and benefit from it
 At first, I wanted to write honestly and in detail about the methods for reducing the dimensionality of the data - PCA , ICA , NMF , throw out a bunch of formulas and say what an important role SVD plays in this whole zoo. Then I realized that the text would be similar to the cutouts from the opuses from Mathgen , so the number of formulas was minimized, but I left the most favorite code and images in full.
At first, I wanted to write honestly and in detail about the methods for reducing the dimensionality of the data - PCA , ICA , NMF , throw out a bunch of formulas and say what an important role SVD plays in this whole zoo. Then I realized that the text would be similar to the cutouts from the opuses from Mathgen , so the number of formulas was minimized, but I left the most favorite code and images in full.I also thought to write about autoencoders. In R, as is well known, the trouble with neural network libraries is either slow , or buggy , or primitive . This is understandable, because without full-fledged GPU support (and this is a huge minus R compared to Python), working with any complex neural networks - and especially with Deep Learning - is practically meaningless (although there is a promising developing project MXNet ). Also of interest is the relatively recent h2o framework, the authors of which are advised by the notorious Trevor Hastie , and Cisco, eBay and PayPal even use it to create their plans to enslave humanity . The framework is written in Java (yes, and loves RAM). Unfortunately, he also does not support working with the GPU, because has a slightly different target audience, but it scales well and provides an interface to R and Python (although fans of masochism can use the web-interface hanging by default on localhost: 54321) .
So, if there is a question about the number of measurements in a data set, then this means that, well, let's say, quite a lot of them, which makes the use of machine learning algorithms not very convenient. And sometimes a piece of data is just information noise, useless trash. Therefore, it is desirable to remove the extra dimensions by pulling out the most valuable of them, if possible. By the way, an inverse problem may arise - add more measurements, and simply more interesting and useful features. Selected components can also be useful for visualization purposes ( t-SNE , for example, is oriented to this). The decomposition algorithms are interesting in their own right as machine learning methods without a teacher, which, you see, sometimes can lead to the solution of the primary problem.
Matrix decomposition
')
In principle, to reduce the dimensionality of data with one or another efficiency, most machine learning methods can be adapted - in fact, they do this, mapping some multidimensional spaces to others. For example, the results of PCA and K-means are equivalent in some sense. But usually you want to reduce the dimension of the data without much fuss with finding model parameters. The most important among such methods, of course, is SVD . “Why SVD, not PCA?” - you ask. Because SVD, firstly, is in itself a separate important method for analyzing data, and the resulting matrix decomposition has quite a meaningful interpretation from the point of view of machine learning; secondly, it can be used for PCA and with some reservations for NMF (as well as other matrix factorization methods); Thirdly, SVD can be tailored to improve the performance of ICA . In addition, SVD does not have such inconvenient properties as, for example, applicability only to square ( LU , Schur expansions) or square symmetric positively defined matrices ( Cholesky ), or only to matrices whose elements are non-negative ( NMF ). Naturally, one has to pay for universality - the singular decomposition is rather slow; therefore, when matrices are too large, randomized algorithms are applied.
The essence of SVD is simple - any matrix (real or complex) is represented as a product of three matrices:
X = UΣV * ,
where U is a unitary matrix of order m; Σ is the mxn matrix, on the main diagonal of which there are non-negative numbers, called singular (the elements outside the main diagonal are zero — such matrices are sometimes called rectangular diagonal matrices); V * is the Hermitian-conjugate matrix of order n to V. The m columns of the matrix U and the n columns of the matrix V are called the left and right singular vectors of the matrix X, respectively. For the problem of reducing the number of dimensions, it is the matrix Σ whose elements, being raised to the second power, can be interpreted as a variance, which each “invests” component, and in descending order: σ 1 ≥ σ 2 ≥ ... ≥ σ noise . Therefore, when choosing the number of components in SVD (as in PCA, by the way), they are guided precisely by the sum of the variances given by the components taken into account. In R, the singular decomposition operation is performed by the svd () function, which returns a list of three elements: the vector dc with singular values, the matrices u and v.
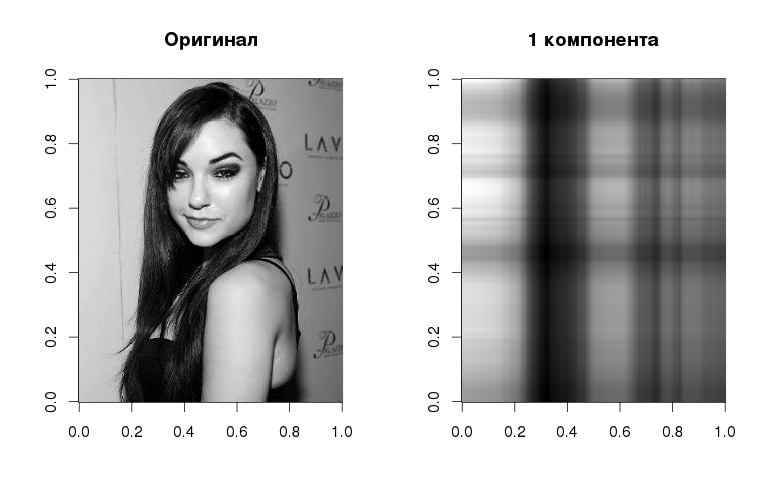
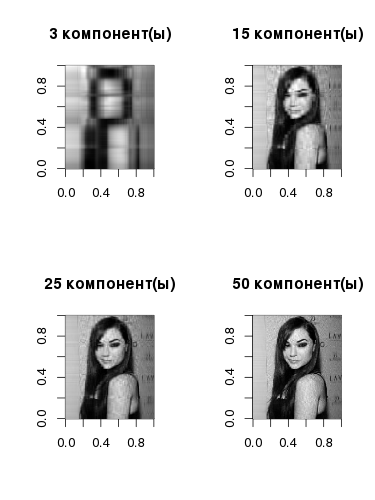
Yes, Sasha looks like this in gray halftones with just one component , but even here you can see the basic linearized structure - in accordance with the gradations in the original image. The component itself is obtained by multiplying the left singular vector by the corresponding singular value and the right singular vector. As the number of vectors increases, the quality of image reconstruction also grows:

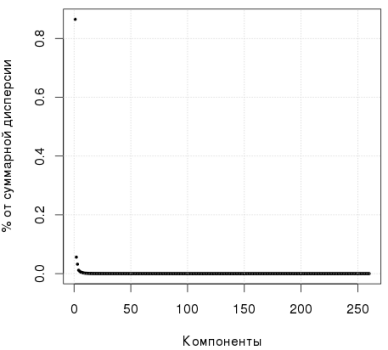
The following graph shows that the first component explains more than 80% of the variance:
Code on R, singular decomposition:
library(jpeg) img <- readJPEG("source.jpg") svd1 <- svd(img) # comp1 <- svd1$u[, 1] %*% t(svd1$v[, 1]) * svd1$d[1] par(mfrow=c(1,2)) image(t(img)[,nrow(img):1], col=gray(0:255 / 255), main="") image(t(comp1)[,nrow(comp1):1], col=gray(0:255 / 255), main="1 ") # par(mfrow=c(2,2)) for (i in c(3, 15, 25, 50)) { comp <- svd1$u[,1:i] %*% diag(svd1$d[1:i])%*% t(svd1$v[,1:i]) image(t(comp)[,nrow(comp):1], col=gray(0:255 / 255), main=paste0(i," ()")) } par(mfrow=c(1,1)) plot(svd1$d^2/sum(svd1$d^2),pch=19,xlab="",ylab="% ", cex=0.4) grid() What will happen if we subtract the average values of each column from the original image, divide the resulting matrix into the square root of the number of columns in the original matrix, and then perform a singular decomposition? It turns out that the columns of the matrix V in the resulting decomposition exactly correspond to the main components, which are obtained by PCA (by the way, in R for PCA, you can use the prcomp () function)
> img2 <- apply(img, 2, function(x) x - mean(x)) / sqrt(ncol(img)) > svd2 <- svd(img2) > pca2 <- prcomp(img2) > svd2$v[1:2, 1:5] [,1] [,2] [,3] [,4] [,5] [1,] 0.007482424 0.0013505222 -1.059040e-03 0.001079308 -0.01393537 [2,] 0.007787882 0.0009230722 -2.512017e-05 0.001324682 -0.01373691 > pca2$rotation[1:2, 1:5] PC1 PC2 PC3 PC4 PC5 [1,] 0.007482424 0.0013505222 -1.059040e-03 0.001079308 -0.01393537 [2,] 0.007787882 0.0009230722 -2.512017e-05 0.001324682 -0.01373691 Thus, when performing the singular decomposition of a normalized initial matrix, it is not difficult to distinguish the main components. This is one of the ways to calculate them; the second is based directly on the search for the eigenvectors of the covariance matrix XX T.
Let us return to the question of choosing the number of principal components. The captain rule is: the larger the component, the more variance they describe. Andrew Ng , for example, advises targeting> 90% of the variance. Other researchers argue that this number may be 50%. Even coined the so-called parallel analysis of Horn, which is based on a Monte Carlo simulation. In R for this package is. A very simple approach is to use a scree plot : on the graph, look for an “elbow” and discard all the components that form the flat part of this “elbow”. In the figure below, I would say that 6 components must be considered:
In general, as you can see. The question is well developed. There is also an opinion that PCA is applicable only for normally distributed data, but the Wiki does not agree with this, and you can use SVD / PCA with data of any distribution, but, of course, it is not always effective (it turns out empirically).
Another interesting decomposition is the factorization of non-negative matrices , which, as the name implies, is used to decompose non-negative matrices into non-negative matrices:
X = WH .
In general, such a problem does not have an exact solution (unlike SVD), and numerical algorithms are used for its calculations. The problem can be formulated in terms of quadratic programming - and in this sense it will be close to SVM . In the problem of reducing the dimension of space, the following is important: if the matrix X has dimension mxn, then the matrix W and H respectively have dimension mxk and kxn, and choosing k is much smaller than m and n themselves, this original dimension can be significantly reduced. NMF likes to be used for analyzing textual data , where non-negative matrices are in good agreement with the very nature of the data, but in general, the range of application of the technique is not inferior to PCA. The decomposition of the first picture in R gives the following result:
Code on R, NMF:
library(NMF) par(mfrow=c(2,2)) for (i in c(3, 15, 25, 50)) { m.nmf <- nmf(img, i) W <- m.nmf@fit@W H <- m.nmf@fit@H X <- W%*%H image(t(X)[,nrow(X):1], col=gray(0:255 / 255), main=paste0(i," ()")) } If you need something more exotic
There is a method that was originally developed for decomposing a signal with additive components — I am talking about ICA . In this case, the hypothesis is accepted that these components have a non-normal distribution, and their sources are independent. The simplest example is a party where a lot of voices are mixed, and the task is to select each sound signal from each source. Two approaches are usually used to search for independent components: 1) with minimization of mutual information based on Kullback-Leibler divergence ; 2) with maximization of “non-Gaussianity” (here measures such as the coefficient of kurtosis and negentropy are used ).
The picture below is a simple example where two sinusoids mix, then they are also highlighted with the help of ICA.

Code on R, ICA:
x <- seq(0, 2*pi, length.out=5000) y1 <- sin(x) y2 <- sin(10*x+pi) S <- cbind(y1, y2) A <- matrix(c(1/3, 1/2, 2, 1/4), 2, 2) y <- S %*% A library(fastICA) IC <- fastICA(y, 2) par(mfcol = c(2, 3)) plot(x, y1, type="l", col="blue", pch=19, cex=0.1, xlab="", ylab="", main=" ") plot(x, y2, type="l", col="green", pch=19, cex=0.1, xlab = "", ylab = "") plot(x, y[,1], type="l", col="red", pch=19, cex=0.5, xlab = "", ylab = "", main=" ") plot(x, y[,2], type="l", col="red", pch=19, cex=0.5, xlab = "", ylab = "") plot(x, IC$S[,1], type="l", col="blue", pch=19, cex=0.5, xlab = "", ylab = "", main="ICA") plot(x, IC$S[,2], type="l", col="green", pch=19, cex=0.5, xlab = "", ylab = "") What does ICA have to do with reducing data dimension? Let us try to present the data - regardless of their nature - as a mixture of components, then it will be possible to divide this mixture into the number of “signals” that suits us. There is no particular criterion, as in the case of PCA, the choice of the number of components is not - it is selected experimentally.
The last test subject in this review is autoencoders , which represent a special class of neural networks that are configured so that the response at the autocoder output is as close as possible to the input signal. With all the power and flexibility of neural networks, we simultaneously get a lot of problems associated with finding the optimal parameters: the number of hidden layers and neurons in them, activation functions ( sigmoid , tanh , ReLu ,), learning algorithm and its parameters, methods of regularization ( L1, L2 , dropout ). If you train an autoencoder on noisy data so that the network restores them, you get denoising autoencoder . Pre-configured auto-encoders can also be "docked" in the form of cascades for pre-training deep networks without a teacher.
In the simplest representation, the autoencoder can be modeled as a multilayer perceptron , in which the number of neurons in the output layer is equal to the number of inputs. From the figure below it is clear that by choosing an intermediate hidden layer of small dimension, we thereby “compress” the original data.

Actually, in the h2o package, which I mentioned above, such an auto-associate is present, so we will use it. At first, I wanted to show an example with gestures , but I quickly became convinced that with a few sentences you would not get off, therefore there will be pictures with handwritten numbers from this competition .

The data is presented in the form of .csv files (train.csv and test.csv), there are quite a lot of them, so in the future, for simplicity, I will work with 10% of the data from train.csv; The column with labels will be used for visualization purposes only. But before we figure out what can be done with an autoencoder, let's see what the first three components give us when decomposing PCA, ICA, NMF:
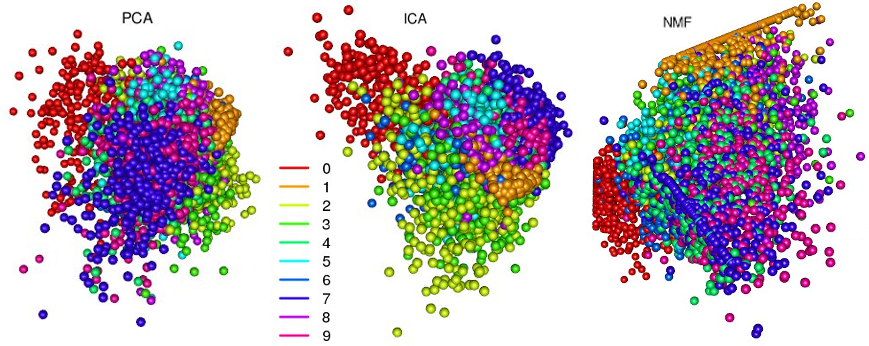
All three methods have coped well with the clustering task — groups are seen more or less clearly in the image, which merge into each other. These transitions are borderline cases where numbers are especially difficult to recognize. In the picture with PCA clusters, it is very noticeable how the principal component method solves an important problem — it decorrelates variables: clusters “0” and “1” are maximally spaced apart. The “unusual” pattern with NMF is connected with the fact that the method works only with non-negative matrices. But such a separation of sets can be obtained using the auto-encoder:
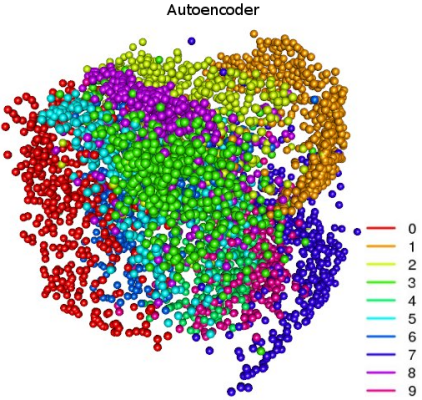
Code on R, h2o autoencoder:
train <- read.csv("train.csv") label <- data$label train$label <- NULL train <- train / max(train) # library(caret) tri <- createDataPartition(label, p=0.1)$Resample1 train <- train[tri, ] label <- label[tri] # h2o library(h2o) h2o.init(nthreads=4, max_mem_size='14G') train.h2o <- as.h2o(train) # m.deep <- h2o.deeplearning(x=1:ncol(train.h2o), training_frame=train.h2o, activation="Tanh", hidden=c(150, 25, 3, 25, 150), epochs=600, export_weights_and_biases=T, ignore_const_cols=F, autoencoder=T) deep.fea <- as.data.frame(h2o.deepfeatures(m.deep, train.h2o, layer=3)) library(rgl) palette(rainbow(length(unique(labels)))) plot3d(deep.fea[, 1], deep.fea[, 2], deep.fea[, 3], col=label+1, type="s", size=1, box=F, axes=F, xlab="", ylab="", zlab="", main="AEC") Here clusters are more clearly defined and spaced apart. The network has a fairly simple architecture with 5 hidden layers and a small number of neurons; in the third hidden layer there are only 3 neurons, and the features from there are just depicted above. Some more fun pictures:

R code, visualization of weights of the first hidden layer:
W <- as.data.frame(h2o.weights(m.deep, 1)) pdf("fea.pdf") for (i in 1:(nrow(W))){ x <- matrix(as.numeric(W[i, ]), ncol=sqrt(ncol(W))) image(x, axes=F, col=gray(0:255 / 255)) } dev.off() In fact, these are just images of the weights of the neurons: each picture is associated with a separate neuron and represents a filter that selects specific information for a given neuron. Here, for comparison, the scales of the output layer:

The above autoencoder is easy to turn into denoising autoencoder. Since such an auto-encoder must be fed distorted images at the input, it is enough to place a dropout layer in front of the first hidden layer . Thanks to him, with some probability, the neurons will be in the "off" state, which a) will distort the processed image; b) will serve as a kind of regularization in training.
Another interesting application of the auto-encoder is the definition of anomalies in the data by the error of image reconstruction. In general, if the data supplied to the input of the autoencoder is not from the training sample, then, of course, the reconstruction error of each image from the new sample will be higher than that of the training sample, but more or less one order of magnitude. If there are anomalies, this error will be dozens or even hundreds of times more.
Conclusion
Of course, it would be wrong to write that some kind of compression method is better or worse than others: each has its own specifics and scope; much depends on the nature of the data itself. Not the last role here is played by the speed of the algorithm. Of the above, SVD / PCA turned out to be the fastest, then ICA, NMF go in order, and the autoencoder completes the series. It is especially difficult to work with the autosociators - not least because of the nontriviality in the selection of parameters.
Source: https://habr.com/ru/post/275273/
All Articles