Algorithm Deflate for example PNG format

As part of another laboratory work, my colleagues and I were faced with the task of parsing a hexadecimal dump of a PNG file. Under the RFC 2083 standard, PNG format stores pixel data compressed with the Deflate algorithm . Therefore, when parsing the dump, we needed to unpack the compressed data using the Inflate algorithm.

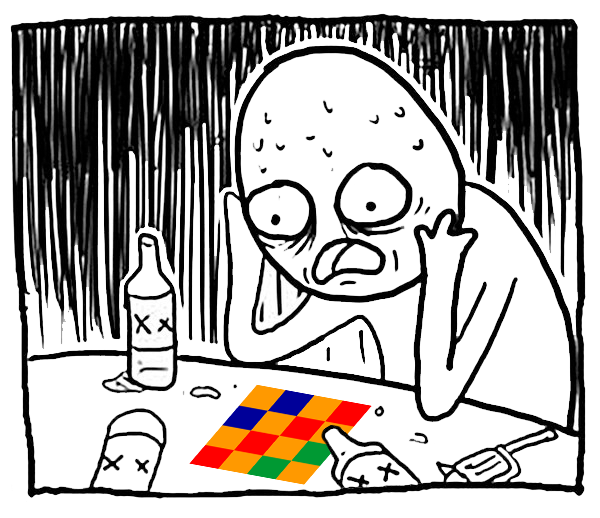
We perform analysis on the following 4x4 pixel image:


')
Compressed using Deflate of the RFC 1951 standard, data streams are stored in PNG in the zlib format of the RFC 1950 standard, we will use this standard for parsing. The zlib header defines the deflate settings. It has the following structure:

1 byte		1 byte			4 bytes
CMF		Flg			Dictid
4 bits	4 bits	2 bits	1 bit	5 bits
CINFO	CM	Flevel	FDICT	FCHECK

Read more about the fields:

• CMF (Compression method and flags). This byte is divided into 2 cells of 4 bits each: CM (Compression method), CINFO (Compression info).
• CM (Compression method). This field defines the compression method used in the file. CM = 8 indicates that Deflate is used with a window size of up to 32 kilobytes.
• CINFO (Compression info). When CM = 8, CINFO is the logarithm with base 2, which sets the window size minus 8 (CINFO = 7, sets the window size to 32 kilobytes).
• FLG (Flags). This byte is divided into parts as follows: FCHECK, FDICT, FLEVEL.
• FCHECK (check bits for CMF and FLG). Consider the value of the expression sum = (CMF * 256 + FLG) as a sixteen-bit integer without a sign. This field complements the FLG so that the sum value is a multiple of 31.
• FDICT (Preset dictionary). If this flag is set, the DICT dictionary descriptor immediately follows the FLG byte. The unpacker can use the value of this field to determine the dictionary that was used during compression.
• FLEVEL (Compression level). This field is used by special compression algorithms. Deflate (CM = 8): 0 - the fastest compression, 1 - the rapid compression, 2 - the default compression, 3 - the maximum compression (most slowly). The value of this field is not taken into account when unpacking. Used to indicate whether additional compression is meaningful.

After DICT (if FDICT is set), there is a stream of compressed data, the length of which for PNG depends on the CHUNK_LENGTH field of the IDAT structure. At the end of the zlib batch, the ADLER-32 checksum is calculated from uncompressed data using the Adler-32 algorithm.

In our case, the zlib header is as follows:

78 DA	0111	1000	eleven	0	11010
	Window size = 32K	Compression method = Deflate	Compression level = fastest	Dictionary is used = false	Check bits

From the title we find out that the dictionary is not used (FDICT = 0).

Compressed data for our image:

63 F8 3F 93 E1 3F 03 C3 CC FF 20 1A C8 00 22 24 0E 58 12 85 33 D3 F8 3F 03 32 07 44 03 00 AA 05 23 77

The bits are then read continuously bytes. In the byte, we go from the last bit to the first bit (for example, 2 bytes in the data stream are successively moving: 63 F8 (0b01100011 0b11111000), then we should receive the following sequence of bits: 1100011000011111).

The first bit in the read sequence is the BFINAL flag, indicating whether this piece of data is the last. The next 2 bits of the BTYPE indicate the type of compression: 00 - uncompressed, 01 - compression with fixed Huffman codes, 10 - compression with dynamic Huffman codes, 11 - the value is reserved.

Table for fixed Huffman codes:

Unpacked value	Number of bits	Codes	base
0 - 143	eight	00110000 to 10111111	00110000
144 - 255	9	110010000 to 111111111	110010000
256 - 279	7	From 0000000 to 0010111	0000000
280 - 287	eight	From 11000000 to 11000111	11000000

Offset table:

Codes	Add. bits	Distance	Codes	Add. bits	Distance	Codes	Add. bits	Distance
0	0	one	ten	four	33 - 48	20	9	1025 - 1536
one	0	2	eleven	four	49 - 64	21	9	1537 2048
2	0	3	12	five	65 - 96	22	ten	2049 - 3072
3	0	four	13	five	97 - 128	23	ten	3073 - 4096
four	one	5, 6	14	6	129 - 192	24	eleven	4097 - 6144
five	one	7, 8	15	6	193 - 256	25	eleven	6145 - 8192
6	2	9 - 12	sixteen	7	257 - 384	26	12	8193 - 12288
7	2	13 - 16	17	7	385 - 512	27	12	12289 - 16384
eight	3	17 - 24	18	eight	513 - 768	28	13	16385 - 24576
9	3	25 - 32	nineteen	eight	769 - 1024	29	13	24577 - 32768

Length table:

Codes	Add. Bits	Length	Codes	Add. Bits	Length	Codes	Add. Bits	Length
257	0	3	267	one	15, 16	277	four	67 - 82
258	0	four	268	one	17, 18	278	four	83 - 98
259	0	five	269	2	19 - 22	279	four	99 - 114
260	0	6	270	2	23 - 26	280	four	115 - 130
261	0	7	271	2	27 - 30	281	five	131 - 162
262	0	eight	272	2	31 - 34	282	five	163 - 194
263	0	9	273	3	35 - 42	283	five	195 - 226
264	0	ten	274	3	43 - 50	284	five	227 - 257
265	one	11, 12	275	3	51 - 58	285	0	258
266	one	13, 14	276	3	59 - 66

When unpacking data can be represented by two types: a fixed value and the length of the reverse bias.

The data that we read must be converted to fixed values. Below is the translation formula:

lit value = data - base + left bound, where
lit value - fixed value
base - a column from table 1,
left bound - the left number from the column of unpacked values ​​from table 1.

When reading data, we can unambiguously determine to which interval of fixed values ​​from Table 1 it corresponds due to the fact that the prefixes of each interval are different.

For example, choose from our sequence 2 bytes F8 and 3F. The bit sequence, which turned out to be 000 111111111 1100. Let the current read position 4, then read 7 bits (the minimum number of bits), we get the prefix 1111111, which corresponds to interval 2. From this it turns out that the length of the read code is 9.

0b111111111 = 0d511

Using the formula above, we get that the number that was coded is 255 = 511-400 (0b110010000) + 144.

Consider the case when, instead of a fixed value, we have a data stream containing information about the length and reverse bias, i.e. The read value falls into the 3rd interval. In our version it will be a subsequence:

20 1A C8 ( 0000010 0 01011000 00010011).

We read the first 7 bits (0b0000010), which fall into the interval 3. By the formula we translate into a number. This will be the number 257 = 1 - 0 + 256. Next, we use table 3. The code 257 means that the number of additional bits to be counted is 0. And the length of the third column is 3. If there are additional bits, they are read in the reverse order . These bits define the number we add to the length.

Next, read 5 bits (0b00101 = 0d5), which determine the reverse offset. In our case, this number is 5. From table 2 it is clear that we need to count 1 extra bit. We read it in reverse order. It turned out 1 (0d1). We add this number to the minimum distance from column 3. And from this it follows that our reverse offset is 7 + 1 = 8.

What does this mean? For example, we counted 9 values: 0 255 153 0 255 0 0 153 255. The inverse distance shows how many values ​​we need to move backward in this stream, i.e. we will be at the second value - 255. The length that we have is 3, shows that we need to take 3 values ​​in from the data stream, starting with the value we are standing on, i.e. 255 153 0. If the length is greater than the offset, then we return to the starting position and reread in the original order until we count the number of values ​​equal to the length. Suppose we have a length of 7, and the reverse offset is 2. We shift by 2 values, i.e. our position on the penultimate number is 153. The sequence that turned out to be 153 255 153 255 153 255 153. In the end, when the unpacker reads the next fixed value equal to zero, it completes its work.

Full analysis of the dump:

01100 01 1 FINAL CHUNK, FIXED HUFFMAN 11111 000 48 - 48 + 0 = 0 - FILTER: NONE 0011 1111 511 - 400 + 144 = 255 100 10011 409 - 400 + 144 = 153 111 00001 48 - 48 + 0 = 0 00 111111 511 - 400 + 144 = 255 00 000011 48 - 48 + 0 = 0 11 000011 48 - 48 + 0 = 0 1 1001100 409 - 400 + 144 = 153 11111111 511 - 400 + 144 = 255 0 0100000 2 - 0 + 256 = 258 LENGTH = 4 000 1 1010 5 DISTANCE = 7 + 1 = 8 1100 1000 1 - 0 + 256 = 257 LENGTH = 3 00000 00 0 6 DISTANCE = 9 + 0 = 9 0 01000 01 1 - 0 + 256 = 257 LENGTH = 3, 2 DISTANCE = 3 0 0 100100 9 - 0 + 256 = 265 LENGTH = 11 + 0 = 11 00 00 1110 7 DISTANCE = 13 + 0 = 13 010 11000 3 - 0 + 256 = 259 LENGTH = 5 000 100 10 9 DISTANCE = 25 + 4 = 29 100 0 0101 10 - 0 + 256 = 266 LENGTH = 13 + 0 = 13 0011 00 11 7 DISTANCE = 13 + 0 = 13 110 10011 409 - 400 + 144 = 153 111 11000 99 - 48 + 0 = 51 00 111111 511 - 400 + 144 = 255 00 000011 48 - 48 + 0 = 0 00 1 10010 9 - 0 + 256 = 265 LENGTH = 11 + 1 = 12 000 00 111 7 DISTANCE = 13 + 0 = 13 0100 0100 2 - 0 + 256 = 258 LENGTH = 4 000000 1 1 5 DISTANCE = 7 + 1 = 8 0000000 0 0 - 0 + 256 = 256 END 10101010 ADLER 00000101 ADLER 00100011 ADLER 01110111 ADLER

0 255 153 0 255 0 0 153 255 255 153 0 255 255 0 0 255 0 0 0 153 255 255 153 0 255 255 0 0 255 255 153 0 255 0 255 153 0 255 255 0 0 255 255 153 0 255 0 153 51 255 0 255 0 0 255 255 153 0 255 0 153 51 255 255 153 0 255

The search for similar materials ultimately led to standards. We hope that this article is already in their native and understandable Russian language will help those in need in their own endeavors.

Source image