Calculation of binomial coefficients using Fourier transforms
When solving problems of combinatorics, it is often necessary to calculate the binomial coefficients. Bin Newton, i.e. decomposition 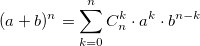 also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials:
also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials: 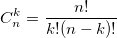 or use the recurrence formula:
or use the recurrence formula: 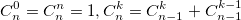 From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers.
From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers.
One of the methods to significantly reduce the number of calculations is the use of Fourier transforms and discrete Fourier transforms.
The presence of a large number of libraries that implement Fourier transforms (in all sorts of fast versions) makes the implementation of algorithms not a very difficult task for programming.
The implemented algorithms are part of the open source FFTTools library. Internet address: github.com/dprotopopov/FFTTools
')
The Fourier transform of the function f by a real variable is integral and is given by the following formula:
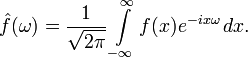
Different sources may give definitions that differ from the above given by choosing the coefficient before the integral, as well as the sign "-" in the exponent. But all the properties will be the same, although the form of some formulas may change.
In addition, there are various generalizations of this concept.
Discrete Fourier transform (in the English-language DFT literature, Discrete Fourier Transform) is one of the Fourier transforms that are widely used in digital signal processing algorithms (its modifications are used in audio compression in MP3, image compression in JPEG, etc.), as well as in other areas associated with the analysis of frequencies in a discrete (for example, digitized analog) signal. The discrete Fourier transform requires a discrete function as an input. Such functions are often created by sampling (sampling values from continuous functions). Discrete Fourier transforms help solve partial differential equations and perform operations such as convolutions. Discrete Fourier transforms are also actively used in statistics when analyzing time series. There are multidimensional discrete Fourier transforms.
Direct conversion:
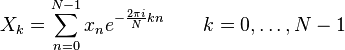
Inverse transform:
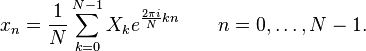
The discrete Fourier transform is a linear transform that translates a vector of time samples into a vector of spectral samples of the same length. Thus, the transformation can be implemented as a multiplication of a symmetric square matrix by a vector:
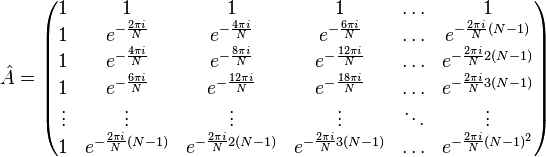
According to the definition, the convolution of two functions F and G is the function FG:
One of the remarkable properties of Fourier transforms is the ability to quickly calculate the correlation of two functions defined, either on a real argument (using the classical formula) or on a finite ring (using discrete transformations).
And although such properties are inherent in many linear transformations, for practical use, to calculate the convolution operation, according to our definition, the formula is used
Where
It is rather easy to verify the equality of equality by explicitly substituting into formulas of Fourier transforms and reducing the resulting formulas
Consider the polynomial F (x) = 1 + x and its convolution with itself n times
Fx..xF = SUM C (i, n-1) * x ^ i = BFT (FFT (F) * ... * FFT (F)) = BFT (FFT (F) ^ (n-1))
That is, the binomial coefficients C (i, n-1) can be obtained from the values of the coefficients of the polynomial (1 + x) ^ (n-1)
When calculating using Pascal's triangle, laboriousness has the estimate O (n ^ 2).
When calculating with the help of fast Fourier transforms, laboriousness has an estimate of O (n * log n).
The article borrows fragments from the article Calculation of binomial coefficients in C (C ++)
PS
The complexity of the calculation of binomial coefficients can be reduced to O (n):
Cn [0] = 1
Cn [i + 1] = Cn [i] * (ni) / (i + 1)
Evidence:
Cn [i] * (ni) / (i + 1) = n! / ((Ni)! I!) * (Ni) / (i + 1) = n! / ((Ni-1)! (I + 1)!) = Cn [i + 1]
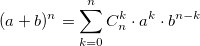 also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials:
also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials: 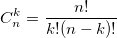 or use the recurrence formula:
or use the recurrence formula: 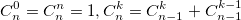 From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers.
From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers.One of the methods to significantly reduce the number of calculations is the use of Fourier transforms and discrete Fourier transforms.
The presence of a large number of libraries that implement Fourier transforms (in all sorts of fast versions) makes the implementation of algorithms not a very difficult task for programming.
The implemented algorithms are part of the open source FFTTools library. Internet address: github.com/dprotopopov/FFTTools
')
The Fourier transform of the function f by a real variable is integral and is given by the following formula:
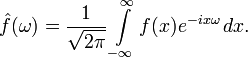
Different sources may give definitions that differ from the above given by choosing the coefficient before the integral, as well as the sign "-" in the exponent. But all the properties will be the same, although the form of some formulas may change.
In addition, there are various generalizations of this concept.
Discrete Fourier Transform
Discrete Fourier transform (in the English-language DFT literature, Discrete Fourier Transform) is one of the Fourier transforms that are widely used in digital signal processing algorithms (its modifications are used in audio compression in MP3, image compression in JPEG, etc.), as well as in other areas associated with the analysis of frequencies in a discrete (for example, digitized analog) signal. The discrete Fourier transform requires a discrete function as an input. Such functions are often created by sampling (sampling values from continuous functions). Discrete Fourier transforms help solve partial differential equations and perform operations such as convolutions. Discrete Fourier transforms are also actively used in statistics when analyzing time series. There are multidimensional discrete Fourier transforms.
Discrete Transform Formulas
Direct conversion:
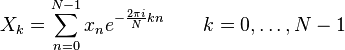
Inverse transform:
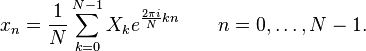
The discrete Fourier transform is a linear transform that translates a vector of time samples into a vector of spectral samples of the same length. Thus, the transformation can be implemented as a multiplication of a symmetric square matrix by a vector:
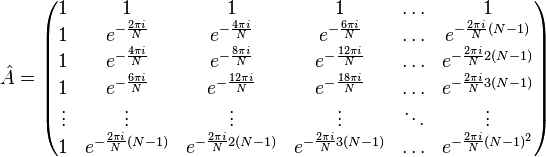
Convolution of two functions
According to the definition, the convolution of two functions F and G is the function FG:
FxG (t) = SUM F (i) * G (j) | i + j = t
Fourier Transforms for Convolution Calculation
One of the remarkable properties of Fourier transforms is the ability to quickly calculate the correlation of two functions defined, either on a real argument (using the classical formula) or on a finite ring (using discrete transformations).
And although such properties are inherent in many linear transformations, for practical use, to calculate the convolution operation, according to our definition, the formula is used
FxG = BFT (FFT (F) * FFT (G))
Where
- FFT - direct Fourier transform operation
- BFT is the operation of the inverse Fourier transform
It is rather easy to verify the equality of equality by explicitly substituting into formulas of Fourier transforms and reducing the resulting formulas
Binomial coefficients
Consider the polynomial F (x) = 1 + x and its convolution with itself n times
Fx..xF = SUM C (i, n-1) * x ^ i = BFT (FFT (F) * ... * FFT (F)) = BFT (FFT (F) ^ (n-1))
That is, the binomial coefficients C (i, n-1) can be obtained from the values of the coefficients of the polynomial (1 + x) ^ (n-1)
We program:
using System; using System.Drawing; using System.Linq; using System.Numerics; namespace FFTTools { public class BinomialBuilder : BuilderBase, IBuilder { /// <summary> /// Performs application-defined tasks associated with freeing, releasing, or resetting unmanaged resources. /// </summary> public void Dispose() { } public static void GetLongs(long[] array, long x = 1) { var n = array.Length - 1; if (array.Length > 0) array[0] = 1; for (var i = 0; i < n; i++) array[i + 1] = x*array[i]*(n - i)/(i + 1); } public static void GetDoubles(double[] array, double x = 1.0) { var complex = new Complex[array.Length]; if (array.Length > 0) complex[0] = Complex.One; if (array.Length > 1) complex[1] = x; if (array.Length > 0) { Fourier(complex, FourierDirection.Forward); complex = complex.Select( value => Complex.Pow(value, array.Length - 1)/array.Length).ToArray(); Fourier(complex, FourierDirection.Backward); } var index = 0; foreach (var value in complex) array[index++] = value.Real; } public Bitmap ToBitmap(Bitmap source) { throw new NotImplementedException(); } } } Checking:
using System; using System.Linq; using Microsoft.VisualStudio.TestTools.UnitTesting; namespace FFTTools.UnitTest { [TestClass] public class BinomialUnitTest { [TestMethod] public void BinomialTestMethod() { const int count = 10; var doubles = new double[count]; var longs = new long[count]; BinomialBuilder.GetLongs(longs); BinomialBuilder.GetDoubles(doubles); Console.WriteLine( string.Join(Environment.NewLine, longs.Zip(doubles, (x, y) => string.Format("{0} - {1} = {2}", x, y, x - y))) + Environment.NewLine); Assert.IsTrue(doubles.Zip(longs, (x, y) => x - y).All(x => Math.Abs(x) < 0.001)); } } } What for?
When calculating using Pascal's triangle, laboriousness has the estimate O (n ^ 2).
When calculating with the help of fast Fourier transforms, laboriousness has an estimate of O (n * log n).
Note:
The article borrows fragments from the article Calculation of binomial coefficients in C (C ++)
PS
The complexity of the calculation of binomial coefficients can be reduced to O (n):
Cn [0] = 1
Cn [i + 1] = Cn [i] * (ni) / (i + 1)
Evidence:
Cn [i] * (ni) / (i + 1) = n! / ((Ni)! I!) * (Ni) / (i + 1) = n! / ((Ni-1)! (I + 1)!) = Cn [i + 1]
Source: https://habr.com/ru/post/274729/
All Articles