Calculation of binomial coefficients in C (C ++) and Python
When solving problems of combinatorics, it is often necessary to calculate the binomial coefficients. Bin Newton, i.e. decomposition 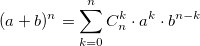 also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials:
also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials: 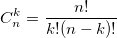 or use the recurrence formula:
or use the recurrence formula: 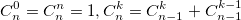 From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers. On this example, I wanted to show that even when solving a simple task, you can step on a rake.
From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers. On this example, I wanted to show that even when solving a simple task, you can step on a rake.
Before proceeding to the writing of calculation procedures, consider the so-called Pascal triangle.
or he, but in a slightly different form. In the left column of the row, the value of n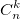 for k = 0..n
for k = 0..n
In full accordance with the recurrent value formula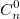 equal to 1 and any number is equal to the sum of the number above it and the number “above it + step to the left”. For example, in the 7th line the number is 21, and in the 6th line the numbers are 15 and 6: 21 = 15 + 6. It is also seen that the values in the line are symmetric about the middle of the line, i.e.
equal to 1 and any number is equal to the sum of the number above it and the number “above it + step to the left”. For example, in the 7th line the number is 21, and in the 6th line the numbers are 15 and 6: 21 = 15 + 6. It is also seen that the values in the line are symmetric about the middle of the line, i.e.  . This is the symmetry property of the Newton binomial with respect to a and b and it can be seen in the factorial formula.
. This is the symmetry property of the Newton binomial with respect to a and b and it can be seen in the factorial formula.
Below for binomial coefficients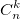 I will also use the C (n, k) representation (it is easier to type it, and the picture-formula can not be inserted everywhere.
I will also use the C (n, k) representation (it is easier to type it, and the picture-formula can not be inserted everywhere.
since the binomial coefficients are non-negative, we will use the unsigned type in the calculations.
')
Call the function bci (10,4) - it will return 210 and this is the correct value of the coefficient C (10.4). So the calculation problem is solved? Yes solved. But not really. We did not answer the question: for what maximum values of n, k will bci function correctly? Before we begin to look for the answer, let's agree that the type used by us is unsigned int 4-byte and the maximum value is 2 32 -1 = 4'294'967'295. For what n, k C (n, k) exceed it? We turn to the triangle of Pascal. It can be seen that the maximum values are reached in the middle of the line with k = n / 2. If n is even, then there is one maximum value, and if n is odd, then there are two. The exact value of C (34.17) is 2333606220, and the exact value of C (35.17) is 4537567650, i.e. already more than the maximum unsigned int.
We write a test procedure
The value in the next line should be about 2 times greater than the previous one. Therefore, the last correctly calculated coefficient (see the triangle above) is C (12.6). Although unsigned int holds 4 billion, values less than 1000 are calculated correctly. Those times why so? It's all about our bci procedure, more precisely in the string that first calculates a large number in the numerator, and then divides it into a large number in the denominator. To calculate C (13,6), first 13 is calculated! And this number is> 6 billion and it does not fit into an unsigned int.
How to optimize the calculation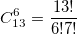 ? Very simple: open the 13! and reduce the numerator and denominator by 7! The result is
? Very simple: open the 13! and reduce the numerator and denominator by 7! The result is 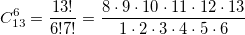 . Let's program the calculation using this formula.
. Let's program the calculation using this formula.
:
Clearly better, the error occurred when calculating C (31.15). The reason is clear - all the same overflow. First, multiply by 31 (op-pa - overflow, then divide by 15). And what if to use the recursive formula? There only addition, overflow should not be.
Well, try:
Everything that got into unsigned int was considered correct. That's just a line with n = 34 was considered about a minute. When calculating C (n, n / 2), two recursive calls are made, so the calculation time depends exponentially on n. What to do - it turns out either inaccurate or slow. Output - in the use of 64 bit variables.
Comment on the results of discussions: a section was added at the end of the article, where a simple and fast version of “bcr with memorization” of one of the participants in the discussion is given.
Replace in the bci unsigned int function with unsigned long long and test it in the range n = 34..68. n = 34 is the maximum value that bci is correctly considered, and C (68.34) ~ 2.8 * 10 19 no longer fits into an unsigned long long ~ 1.84 * 10 19
We see that the error occurs when n = 63 for the same reason as in bci. First multiply by 63 (and overflow), then division by 31.
The error occurred when n = 63, and when n = 68, the result no longer fits into unsigned64. Therefore, it can be said that “up to n <= 62, the bcl function is correct, a further increase in accuracy requires either int128 or a long arithmetic”. And if a very high accuracy is not needed, but I want to consider the binomial coefficients for n = 100 ... 1000? Again, we take the bci procedure and change the unsigned int types to double in it:
Even for n = 1000 it was possible to count! Overflow double will occur when n = 1030.
The discrepancy between the bcd calculation and the exact value starts with n = 57. It is small - only 8. With n = 67, the deviation is 896.
In principle, for practical problems, the accuracy of the bcd function is sufficient, but in olympiad problems, tests are often given “on the verge”. Those. theoretically, there may be a problem where double accuracy is not enough and C (n, k) fits into an unsigned long long barely. How to avoid overflow for such extreme cases? You can use a recursive algorithm. But if he counted a minute for n = 34, then he would count years 100 for n = 67. You can memorize the calculated values (see Addition after publishing). You can also use recursion not for all n and k, but only for “big enough”. Here is the calculation procedure that counts correctly for n <= 67. Sometimes for n> 67 with small k (for example, it considers C (82.21) = 1.83 * 10 19 ).
In one of the olympiad tasks I needed to calculate a lot of C (n, k) for n> 70, i.e. They obviously did not fit into an unsigned long long. Naturally, I had to use "long arithmetic" (my own). For this task, I wrote a “recursion with memory”: the calculated coefficients were stored in the array and there was no exponential increase in the calculation time.
When discussing, options with memorization of calculated values are often mentioned. I have a code with dynamic memory allocation, but I did not bring it. For the time being, here is the simplest and most effective of the chersanya comment: http://habrahabr.ru/post/274689/#comment_8730359http://habrahabr.ru/post/274689/#comment_8730359
If the program should use [almost] all the coefficients of Pascal's triangle (to some level), then the reduced recursive algorithm with memorization is the fastest way. Similar code is also suitable for unsigned long long and even for long arithmetic (although there, probably, it is better to dynamically calculate and allocate the required amount of memory). Specific values for N_MAX can be:
35 - count all coefficients C (n, k), n <35 for unsigned int (32 bits)
68 - count all coefficients C (n, k), n <68 for unsigned long long (64 bits)
200 - calculate the coefficients C (n, k), n <200 and some k for unsigned long long (64 bits). For example, for C (82.21) = ~ 1.83 * 10 19
K_MAX - this can be N_MAX / 2 + 1, but not more than 35, since C (68,34) is unsigned long long abroad.
For simplicity, you can always take K_MAX = 35 and not think “go in - not go in” (until we go to numbers with a bit depth> 64 bits).
This supplement appeared about the weather after the publication of the article. The author began to learn Python and for the training I solve the olimpiadnye tasks made earlier in C ++. For tasks related to exact / long calculations, one has to either contrive in every way (as in the calculations of binomial coefficients), in order to avoid early overflow, or accept the loss of accuracy (by going to double type) or write (or search) long arithmetic. In Python, long arithmetic is already there, so memorization is sufficient to calculate the binomial coefficients. We will memorize them in the list (passed to the function as a papameter).
Here is the output (without label)
270288240945436569515614693625975275496152008446548287007392875106625428705522193898612483924502370165362606085021546104802209750050679917549894219699518475423665484263751733356162464079737887344364574161119497604571044985756287880514600994219426752366915856603136862602484428109296905863799821216320
0.4200884663301988
Less than half a second for this ratio
C (68.34) (remember , it does not fit into a long long) is calculated in 0.017 seconds and is equal to 28453041475240576740
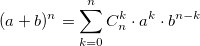 also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials:
also uses binomial coefficients. For their calculation, you can use the formula expressing the binomial coefficient through factorials: 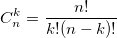 or use the recurrence formula:
or use the recurrence formula: 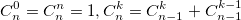 From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers. On this example, I wanted to show that even when solving a simple task, you can step on a rake.
From the Newton binomial and the recurrent formula, it is clear that the binomial coefficients are integers. On this example, I wanted to show that even when solving a simple task, you can step on a rake.Before proceeding to the writing of calculation procedures, consider the so-called Pascal triangle.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 or he, but in a slightly different form. In the left column of the row, the value of n
 for k = 0..n
for k = 0..n n 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 7 1 7 21 35 35 21 7 1 8 1 8 28 56 70 56 28 8 1 9 1 9 36 84 126 126 84 36 9 1 10 1 10 45 120 210 252 210 120 45 10 1 11 1 11 55 165 330 462 462 330 165 55 11 1 12 1 12 66 220 495 792 924 792 495 220 66 12 1 13 1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1 14 1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1 15 1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1 16 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1 In full accordance with the recurrent value formula
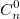 equal to 1 and any number is equal to the sum of the number above it and the number “above it + step to the left”. For example, in the 7th line the number is 21, and in the 6th line the numbers are 15 and 6: 21 = 15 + 6. It is also seen that the values in the line are symmetric about the middle of the line, i.e.
equal to 1 and any number is equal to the sum of the number above it and the number “above it + step to the left”. For example, in the 7th line the number is 21, and in the 6th line the numbers are 15 and 6: 21 = 15 + 6. It is also seen that the values in the line are symmetric about the middle of the line, i.e.  . This is the symmetry property of the Newton binomial with respect to a and b and it can be seen in the factorial formula.
. This is the symmetry property of the Newton binomial with respect to a and b and it can be seen in the factorial formula.Below for binomial coefficients
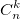 I will also use the C (n, k) representation (it is easier to type it, and the picture-formula can not be inserted everywhere.
I will also use the C (n, k) representation (it is easier to type it, and the picture-formula can not be inserted everywhere.Calculation of binomial coefficients using a factorial formula
since the binomial coefficients are non-negative, we will use the unsigned type in the calculations.
// n unsigned fakt(int n) { unsigned r; for (r=1;n>0;--n) r*=n; return r; } // C(n,k) unsinged bci(int n,int k) { return fakt(n)/(fakt(k)*fakt(nk)); } ')
Call the function bci (10,4) - it will return 210 and this is the correct value of the coefficient C (10.4). So the calculation problem is solved? Yes solved. But not really. We did not answer the question: for what maximum values of n, k will bci function correctly? Before we begin to look for the answer, let's agree that the type used by us is unsigned int 4-byte and the maximum value is 2 32 -1 = 4'294'967'295. For what n, k C (n, k) exceed it? We turn to the triangle of Pascal. It can be seen that the maximum values are reached in the middle of the line with k = n / 2. If n is even, then there is one maximum value, and if n is odd, then there are two. The exact value of C (34.17) is 2333606220, and the exact value of C (35.17) is 4537567650, i.e. already more than the maximum unsigned int.
We write a test procedure
void test() { for (n=10;n<=35;++n) printf("%u %u",n,bci(n,n/2); // C++ cout<<n<<" "<<bci(n,n/2)<<endl; } Run it and see
10 252 11 462 12 924 13 532 14 50 15 9 16 1 17 2 18 1 19 0 20 0 21 1 22 0 23 4 24 1 25 0 26 1 27 0 28 1 29 0 30 0 31 0 32 2 33 2 34 0 35 0 The value in the next line should be about 2 times greater than the previous one. Therefore, the last correctly calculated coefficient (see the triangle above) is C (12.6). Although unsigned int holds 4 billion, values less than 1000 are calculated correctly. Those times why so? It's all about our bci procedure, more precisely in the string that first calculates a large number in the numerator, and then divides it into a large number in the denominator. To calculate C (13,6), first 13 is calculated! And this number is> 6 billion and it does not fit into an unsigned int.
How to optimize the calculation
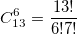 ? Very simple: open the 13! and reduce the numerator and denominator by 7! The result is
? Very simple: open the 13! and reduce the numerator and denominator by 7! The result is 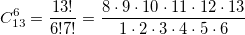 . Let's program the calculation using this formula.
. Let's program the calculation using this formula. unsigned bci(int n,int k) { if (k>n/2) k=nk; // k, nk.. C(n,k)=C(n,nk) if (k==1) return n; if (k==0) return 1; unsigned r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } return r; } :
and test again
10 252 11 462 12 924 13 1716 14 3432 15 6435 16 12870 17 24310 18 48620 19 92378 20 184756 21 352716 22 705432 23 1352078 24 2704156 25 5200300 26 10400600 27 20058300 28 40116600 29 77558760 30 155117520 31 14209041 32 28418082 33 39374192 34 78748384 35 79433695 Clearly better, the error occurred when calculating C (31.15). The reason is clear - all the same overflow. First, multiply by 31 (op-pa - overflow, then divide by 15). And what if to use the recursive formula? There only addition, overflow should not be.
Well, try:
unsigned bcr(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; return bcr(n-1,k)+bcr(n-1,k-1); } void test() { for (n=10;n<=35;++n) printf("%u %u",n,bcr(n,n/2); // C++ cout<<n<<" "<<bcr(n,n/2)<<endl; } Test result
10 252 11 462 12 924 13 1716 14 3432 15 6435 16 12870 17 24310 18 48620 19 92378 20 184756 21 352716 22 705432 23 1352078 24 2704156 25 5200300 26 10400600 27 20058300 28 40116600 29 77558760 30 155117520 31 300540195 32 601080390 33 1166803110 34 2333606220 35 242600354 Everything that got into unsigned int was considered correct. That's just a line with n = 34 was considered about a minute. When calculating C (n, n / 2), two recursive calls are made, so the calculation time depends exponentially on n. What to do - it turns out either inaccurate or slow. Output - in the use of 64 bit variables.
Comment on the results of discussions: a section was added at the end of the article, where a simple and fast version of “bcr with memorization” of one of the participants in the discussion is given.
Using 64 bit types to calculate C (n, k)
Replace in the bci unsigned int function with unsigned long long and test it in the range n = 34..68. n = 34 is the maximum value that bci is correctly considered, and C (68.34) ~ 2.8 * 10 19 no longer fits into an unsigned long long ~ 1.84 * 10 19
unsigned long long bcl(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; unsigned long long r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } return r; } void test() { for (n=34;n<=68;++n) printf("%llu %llu",n,bcl(n,n/2)); // C++ cout<<n<<" "<<bcl(n,n/2)<<endl; } Test result
34 2333606220 35 4537567650 36 9075135300 37 17672631900 38 35345263800 39 68923264410 40 137846528820 41 269128937220 42 538257874440 43 1052049481860 44 2104098963720 45 4116715363800 46 8233430727600 47 16123801841550 48 32247603683100 49 63205303218876 50 126410606437752 51 247959266474052 52 495918532948104 53 973469712824056 54 1946939425648112 55 3824345300380220 56 7648690600760440 57 15033633249770520 58 30067266499541040 59 59132290782430712 60 118264581564861424 61 232714176627630544 62 465428353255261088 63 321255810029051666 64 66050867754679844 65 454676336121653775 66 350360427585442349 67 23341572944240599 68 46683145888481198 We see that the error occurs when n = 63 for the same reason as in bci. First multiply by 63 (and overflow), then division by 31.
Further improvement of accuracy and calculation for n> 67
The error occurred when n = 63, and when n = 68, the result no longer fits into unsigned64. Therefore, it can be said that “up to n <= 62, the bcl function is correct, a further increase in accuracy requires either int128 or a long arithmetic”. And if a very high accuracy is not needed, but I want to consider the binomial coefficients for n = 100 ... 1000? Again, we take the bci procedure and change the unsigned int types to double in it:
double bcd(int n,int k) { if (k>n/2) k=nk; // k, nk.. C(n,k)=C(n,nk) if (k==1) return n; if (k==0) return 1; double r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } return ceil(r-0.2); // , // : , // . - 0.5 round } void testd() { for (n=50;n<=1000;n+=50) printf("%d %.16e\n",n,bcd(n,n/2)); // C++ cout<<n<<" "<<bcd(n,n/2)<<endl; } Test result
50 1.2641060643775200e + 014
100 1.0089134454556417e + 029
150 9.2826069736708704e + 043
200 9.0548514656103225e + 058
250 9.1208366928185793e + 073
300 9.3759702772827310e + 088
350 9.7744946171567713e + 103
400 1.0295250013541435e + 119
450 1.0929255500575370e + 134
500 1.1674431578827770e + 149
550 1.2533112137626624e + 164
600 1.3510794199619429e + 179
650 1.4615494992533863e + 194
700 1.5857433585316801e + 209
750 1.7248900341772600e + 224
800 1.8804244186835327e + 239
850 2.0539940413411323e + 254
900 2.2474718820660189e + 269
950 2.4629741379276902e + 284
1000 2.7028824094543663e + 299
100 1.0089134454556417e + 029
150 9.2826069736708704e + 043
200 9.0548514656103225e + 058
250 9.1208366928185793e + 073
300 9.3759702772827310e + 088
350 9.7744946171567713e + 103
400 1.0295250013541435e + 119
450 1.0929255500575370e + 134
500 1.1674431578827770e + 149
550 1.2533112137626624e + 164
600 1.3510794199619429e + 179
650 1.4615494992533863e + 194
700 1.5857433585316801e + 209
750 1.7248900341772600e + 224
800 1.8804244186835327e + 239
850 2.0539940413411323e + 254
900 2.2474718820660189e + 269
950 2.4629741379276902e + 284
1000 2.7028824094543663e + 299
Even for n = 1000 it was possible to count! Overflow double will occur when n = 1030.
The discrepancy between the bcd calculation and the exact value starts with n = 57. It is small - only 8. With n = 67, the deviation is 896.
For extreme sports and "Olympians"
In principle, for practical problems, the accuracy of the bcd function is sufficient, but in olympiad problems, tests are often given “on the verge”. Those. theoretically, there may be a problem where double accuracy is not enough and C (n, k) fits into an unsigned long long barely. How to avoid overflow for such extreme cases? You can use a recursive algorithm. But if he counted a minute for n = 34, then he would count years 100 for n = 67. You can memorize the calculated values (see Addition after publishing). You can also use recursion not for all n and k, but only for “big enough”. Here is the calculation procedure that counts correctly for n <= 67. Sometimes for n> 67 with small k (for example, it considers C (82.21) = 1.83 * 10 19 ).
unsigned long long bcl(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; unsigned long long r; if (n+k>=90) { // , r=bcl(n-1,k); r+=+bcl(n-1,k-1); } else { r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } } return r; } In one of the olympiad tasks I needed to calculate a lot of C (n, k) for n> 70, i.e. They obviously did not fit into an unsigned long long. Naturally, I had to use "long arithmetic" (my own). For this task, I wrote a “recursion with memory”: the calculated coefficients were stored in the array and there was no exponential increase in the calculation time.
Supplement after publication
When discussing, options with memorization of calculated values are often mentioned. I have a code with dynamic memory allocation, but I did not bring it. For the time being, here is the simplest and most effective of the chersanya comment: http://habrahabr.ru/post/274689/#comment_8730359http://habrahabr.ru/post/274689/#comment_8730359
unsigned bcr_cache[N_MAX][K_MAX] = {0}; unsigned bcr(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; if (bcr_cache[n][k] == 0) bcr_cache[n][k] = bcr(n-1,k)+bcr(n-1,k-1); return bcr_cache[n][k]; } If the program should use [almost] all the coefficients of Pascal's triangle (to some level), then the reduced recursive algorithm with memorization is the fastest way. Similar code is also suitable for unsigned long long and even for long arithmetic (although there, probably, it is better to dynamically calculate and allocate the required amount of memory). Specific values for N_MAX can be:
35 - count all coefficients C (n, k), n <35 for unsigned int (32 bits)
68 - count all coefficients C (n, k), n <68 for unsigned long long (64 bits)
200 - calculate the coefficients C (n, k), n <200 and some k for unsigned long long (64 bits). For example, for C (82.21) = ~ 1.83 * 10 19
K_MAX - this can be N_MAX / 2 + 1, but not more than 35, since C (68,34) is unsigned long long abroad.
For simplicity, you can always take K_MAX = 35 and not think “go in - not go in” (until we go to numbers with a bit depth> 64 bits).
Calculation of binomial coefficients in Python
This supplement appeared about the weather after the publication of the article. The author began to learn Python and for the training I solve the olimpiadnye tasks made earlier in C ++. For tasks related to exact / long calculations, one has to either contrive in every way (as in the calculations of binomial coefficients), in order to avoid early overflow, or accept the loss of accuracy (by going to double type) or write (or search) long arithmetic. In Python, long arithmetic is already there, so memorization is sufficient to calculate the binomial coefficients. We will memorize them in the list (passed to the function as a papameter).
# , / # bcs , n=4 k=2 def Binc(bcs,n,k): if (k>n): return 0 if k>n//2: k=nk # - if k==0: return 1 if k==1: return n while len(bcs)<n-3: # for i in range(len(bcs),n-3): r=[] for j in range(2,i//2+3): r.append(Binc(bcs,i+3,j-1)+Binc(bcs,i+3,j)) bcs.append(r) r=bcs[n-4] if len(r)<k-1: # for i in range(len(r),k-1): r.append(Binc(bcs,n-1,k-1)+Binc(bcs,n-1,k)) return bcs[n-4][k-2] # # C(1000,500) bcs=[] # t1=time.clock() print(Binc(bcs,1000,500)) t2=time.clock() print(t2-t1) # for n in range(0,16): print("n=%2d " % n,end="") for k in range(0,n+1): print("%5d" % Binc(bcs,n,k),end="") print() Here is the output (without label)
270288240945436569515614693625975275496152008446548287007392875106625428705522193898612483924502370165362606085021546104802209750050679917549894219699518475423665484263751733356162464079737887344364574161119497604571044985756287880514600994219426752366915856603136862602484428109296905863799821216320
0.4200884663301988
Less than half a second for this ratio
C (68.34) (remember , it does not fit into a long long) is calculated in 0.017 seconds and is equal to 28453041475240576740
Source: https://habr.com/ru/post/274689/
All Articles