At the end of last year, Google Translate for the release of a new episode of Star Wars added support for Galactic Language Aurebesh. True, it turned out that choosing this language simply translates into English. If you use Chrome or Firefox, then a font appears in which the aubrebesh symbols are substituted for the Latin alphabet, and English text is displayed in IE without any special tricks.

Began to recall other examples of the creation of "foreign languages." For example, the Klingon language from Star Trek is also based on the Latin alphabet, but at the same time it is sufficiently developed and has its own syntax and dictionary. The languages ​​of the peoples of Middle-earth from The Lord of the Rings are a separate story altogether.

There are also languages ​​such as Linkos, specially designed by Hans Freudenthal for interplanetary communication and based on the assumption that mathematics is the universal language of communication for all intelligent beings.

Terry Pratchett also has enough languages ​​in the "Flat World", but it seems that these are just renamed terrestrial languages. And with respect to mathematics, as a universal language, it is more appropriate to mention the English biologist Jack Cohen, his co-author of the book "Science of the Flat World", which at one conference raised a rather unexpected topic: "Why do you think that aliens will understand your mathematics? What if they have a completely different way of thinking? ”
')
I read this quote from James Naishin, another conference participant, a university professor in Hawaii, where she passed. On his website you can find the texts of two speeches, to some extent provoked by this issue: “How do aliens do math” and “Logic of other planets”. Maybe this does not look very serious, especially when different types of logic are attributed to the inhabitants of different planets of our solar system. However, I looked for possible references to one function used to create reversible gates, and I was surprised to find it in the section devoted to the logic of the inhabitants of Jupiter.

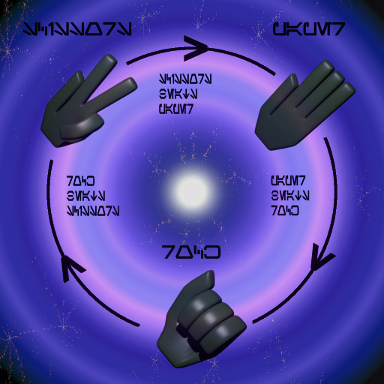
Rock Paper Scissors

What is special about Jupiter’s Logic and how is it related to reversible computations? For its description, Neyshin uses a set of three elements, denoted by the symbols R, P, S, which correspond to the first letters of the English words for stone, scissors and paper. The game “rock, scissors, paper” (they also wrote about it here more than once ) is also known in Hawaii as “jiang-ken.” According to the rules of the game, one of the three items wins the other based on a cyclical set of preferences. This is usually depicted in a pie chart, but can also be written in a line:

S <- R <- P <- S

The mathematical symbol of the relation “precedes” (Unicode 227A) used in the picture is absent in many fonts, therefore in the text it is replaced by <-

How does this relate to logic? It is known that if we equate FALSE = 0, TRUE = 1, then “AND” corresponds to the function “minimum”, and “OR” - “maximum”. The same technique is used in a multi-valued and fuzzy logic , since with this definition many properties of ordinary logic are automatically performed. So, the task of relations between elements defines analogs of logical operations. However, with a cyclical set of preferences between the three elements, some properties have to be sacrificed. What to do, a different logic.

The table for the analogue "OR" with this approach looks like

Other OR	R	P	S
R	R	P	R
P	P	P	S
S	R	S	S

The table for the operation "And" costs the same

Other and	R	P	S
R	R	R	S
P	R	P	P
S	S	P	S

Reversible computations

And what about reversible computations? Already here they wrote about them as well, however, and about the ternary logic ( here , at geektimes , still here ) and even tried to bring them together.

Reversible gates can be useful for solving the problem of heat generation in processors of next generations, they are closely related to the theory of quantum computing. And the topic itself is quite interesting. There are many places to read about this, including the links above, so I’ll try not to cover the subject of already quite well-known things.

If it is very short, the valve is reversible, when the values ​​at the inputs can always be restored by the values ​​at the outputs. To work with binary data, Toffoli or Fredkin universal gates are usually used. Both gates have three inputs and three outputs, since, unlike the irreversible case, from a reversible binary valve with two inputs it is impossible to create a set to perform an arbitrary operation on data.

Let us try to present a reversible analogue of the usual OR valve. Suppose that it has two inputs (and two outputs, since it must be reversible), binary values ​​are fed to the inputs, and one of the outputs must produce the result of the operation "OR". It turns out that the same value 1 (TRUE) at this output can be obtained with three different combinations of inputs: 11, 01, 10. If the second output could have three different values, this could be used to reverse such a gate.

So, already quite simple estimates lead to the idea of ​​using a ternary system on at least one output. And what if you try to work with three values ​​on all inputs and outputs - is it possible to get a reversible valve, if you use the ternary logic?

The triple logic of Lukasevich is quite common. It can also be constructed by the above-mentioned trick with a maximum and a minimum, if we assume that the third value corresponds to some number x, 0 <x <1, for example, x = 1/2. Well-known triple tables are obtained, for "OR":

"Trinity OR"	0	x	one
0	0	x	one
x	x	x	one
one	one	one	one

For and":

"Trinity And"	0	x	one
0	0	0	0
x	0	x	x
one	0	x	one

Suppose again that we have a three-way valve with two inputs and two outputs. One of the above functions is fed to the first output. Is it possible to select a function for the second output so that the valve is reversible. It turns out you can not. The fact is that for an arbitrary reversible function in a 3x3 table describing any input, all values ​​must occur three times.

Indeed, nine possible value pairs can be input.
00 01 0x 10 11 1x x0 x1 xx

and since the valve is reversible, each of these nine pairs should appear at the output with one of the combinations at the input. It can be seen that in these pairs any value of the first (and second) element will occur three times.

That is, three zeros, three units, three X's. Instead, the table for the threefold "OR" is only one zero and five units. In the second table for "And" on the contrary, five zeros and one unit, which is also not suitable.

Therefore, although reversible ternary valves separately and the ternary logic separately are widely used, it is difficult to reduce them together. This is where the "alien" logic comes to the rescue. For clarity, let's replace R, P, S by 0,1, $.



Here is the table for "OR"

"Other OR"	0	one	$
0	0	one	0
one	one	one	$
$	0	$	$

For the values ​​0, 1, it coincides with the usual “OR”, but at the same time it has the already mentioned property necessary to create a reversible three-way valve (each value occurs three times). The situation with the table for operation "And" is similar

"Other And"	0	one	$
0	0	0	$
one	0	one	one
$	$	one	$

Now, in order to build a complete version of reversible ternary valves, one must also select a table for the second, auxiliary output. In ordinary arithmetic, b – a could be used to invert the function max (a, b) at the second output. Something similar can be used in our example.

"Other Difference"	0	one	$
0	0	$	one
one	one	0	$
$	$	one	0

It came - this is how the full three-way reversible OR valve will look

entrance	00	01	$ 0	ten	eleven	1 $	$ 0	$ 1	$$
Output	00	eleven	$ 0	1 $	ten	$ 1	01	$$	$ 0

It can be seen that each of the nine possible combinations occurs at the output once, so the operation is reversible. The effect of this valve can also be described as follows: it does not change the pairs 00, 0 $, rearranging seven pairs in a cycle (01, 11, 10, 1 $, $ 1, $$, $ 0)

So, a sevenfold valve application will leave any pair of values ​​unchanged, and the inverse operation corresponds to the use of six valves in a row. With valves Toffoli and Fredkin easier, each of them coincides with its opposite.

If only zero and one values ​​are input, then this ternary valve implements the usual logical operation "OR." By setting the unit to the second input, you can use the second output as an “NOT” operation from the first input. In addition, the valve implements the operation of “ramification” of the binary value applied to the second input, if zero is given to the first one. So this reversible ternary valve is universal for working with binary data.

An example of a reversible three-way valve "And" is similar

entrance	00	01	$ 0	ten	eleven	1 $	$ 0	$ 1	$$
Output	00	01	$$	$ 0	ten	eleven	$ 1	1 $	$ 0

This valve does not change the pair 00 and 01, rearranging the pair on the cycle
(0 $, $$, $ 0, $ 1, 1 $, 11, 10, 0 $)

It is also universal for binary operations, but unlike “OR”, one such valve is not enough for “ramification”. True, the choice of operation at the second exit was quite arbitrary. The operation at the first input is uniquely determined by the choice of three conditions: (1) perform the necessary logical operation for binary data, (2) match one of the input values, (3) do not depend on their permutation.

The choice of the second operation is also quite natural and can be used for other models. Suppose you need to build a reversible gate for Lukasevich’s logic. The problem with this has already been described, some values ​​appear in the 3x3 table five times, and they must be equal to make a reversible valve.

More lizard and Spock

Here you can apply the same idea as when expanding binary logic to a system of three elements and based on the existing problem with five repetitions in the table for the Lukasevich ternary logic (0, 1, x), you need to add two more elements ($ and @) . Another argument in favor of five values ​​is associated with the use of an analogue of the difference ba for reversing the maximum and minimum: the difference between three integer values ​​from 0 to 2 can take five different values ​​from -2 to 2.

The relationship between the elements can again be depicted in a pie chart or written in a line
0 <- 1 <- $ <- x <- @ <- 0 <- x <- 1 <- @ <- $ <- 0

The corresponding game is also known. For example, her version was shown in the series The Big Bang Theory ( picture with explanation ). You can choose the following correspondences: 0 - stone, 1 - paper, $ - scissors, @ - lizard, x - Spock (native of Vulcan planet in the TV series “Star Trek”).



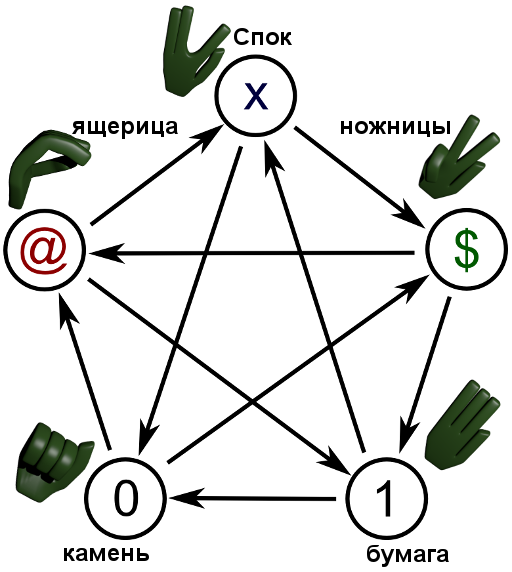
You can continue further; for building similar pie charts, sets in which the number of elements is equal to a prime number are particularly well suited.

Collective logic and "impossible arrows"

I must say that cyclical logic is not such an "alien". One of the most characteristic examples is related to Condorcet and Arrow's paradoxes related to the problem of choice. A typical description of the “voting paradox” can be found in the book of the Nobel Prize in economics Kenneth Arrow “Collective Choice and Individual Values”.

Consider the choice of three alternatives (for example, elections with three candidates) A, B, C. At the same time, each voter has a certain ordered system of preferences. That is, if the first alternative is preferable to the second, and the second is preferable to the third, then the first is also preferable to the third. An example of problems with selection arising from the violation of this criterion is also described below.

Such ordered preferences are an example of transitive relations, and operations with a similar property are associative, that is, do not depend on the arrangement of brackets. The previously discussed definition of the operation “OR” through the assignment of element relations agrees well with the idea of ​​choice: the operation “A OR B” is simply a choice between A and B, based on a certain set of preferences (including the case of “A OR A”, which, although difficult called “choice” also has a well-defined result, A).

Let someone supposes that B is better than A, C is better than B (and by the criterion given earlier, C is better than A). We write this choice as
(1) A <B <C
Suppose there are two other ordered sets of preferences.
(2) B <C <A
(3) C <A <B
Denote the share of voters with the appropriate set of preferences as P1, P2, P3. Then the proportion that consider that B is better than A will be P1 + P3, and those who think that C is better than B will be P1 + P2, but at the same time, P2 + P3 think that A is better than C.

If all values ​​of P1 + P2, P2 + P3, P1 + P3 are more than half (or, equivalently, any proportion of P1, P2, P3 is less than half), then B wins A, C wins B, and A wins C A cyclical system of collective preferences is formed, which, in order to avoid misunderstanding, we denote the already used icon for a relationship without the transitivity property
A <- B <- C <- A.

Even with each individual having an ordered set of preferences, without transitivity, collective choice is no longer unique. The result of the election may depend on the order of conduct and in general be arbitrary. Below are examples of three electoral schemes with a different voting order, leading to the victory of any of the three candidates.

Scheme 1
First round: choice between A and B, beating B
Second round: choice between B (the winner in the first stage) and C,
wins C (in the second round and in elections)

Scheme 2
First round: choice between B and C, beating C
Second round: choice between C and A, in elections wins A

Scheme 3
First round: choice between A and C, wins A
Second round: choice between B and A, wins in elections B

The same problem can be illustrated as a lack of associativity in a cyclical system of preferences. Denote the selection operation as ||

Then the first two schemes correspond to the arrangement of brackets.

((A || B) || C) = B || C = C,
(A || (B || C)) = A || C = A