Geekly Articles each Day
📜 ⬆️ ⬇️

Low-level optimization of parallel algorithms or SIMD in .NET

image

Currently, a huge number of tasks require high system performance. Infinitely increasing the number of transistors on a processor chip does not allow physical limitations. The geometrical dimensions of transistors cannot be physically reduced, since when the permissible dimensions are exceeded, phenomena that are not noticeable with large sizes of active elements begin to manifest themselves - quantum size effects begin to have a strong effect. Transistors do not start working as transistors.
And Moore's law has nothing to do with it. This was and remains the law of value, and an increase in the number of transistors on a chip is rather a consequence of the law. Thus, in order to increase the power of computer systems we have to look for other ways. This is the use of multiprocessors, multicomputers. This approach is characterized by a large number of processor elements, which leads to independent execution of subtasks on each computing device.


Parallel processing methods:

Source of concurrencyAccelerationProgrammer effortPopularity
Many cores2x-128xModerateHigh
Many cars1x-InfinityModerately highHigh
Vectorization2x-8xModerateLow
Graphics cards128x-2048xHighLow
Coprocessor40x-80xModerately highExtremely low

There are many ways to improve the efficiency of systems and they are all quite different. One of such methods is the use of vector processors, which significantly increase the speed of calculations. Unlike scalar processors that process one data element per instruction (SISD), vector processors are capable of processing several data elements (SIMD) per instruction. Most modern processors are scalar. But many of the tasks that they solve require a large amount of computation: video processing, sound processing, work with graphics, scientific calculations, and much more. To speed up the computation process, processor manufacturers began to build additional streaming SIMD extensions into their devices.
Accordingly, with a certain programming approach, it became possible to use vector data processing in the processor. Existing extensions: MMX, SSE and AVX. They allow you to use additional features of the processor for accelerated processing of large data arrays. At the same time, vectorization allows to achieve acceleration without explicit parallelism. Those. it is from the point of view of data processing, but from the point of view of the programmer, this does not require any development costs of special algorithms to prevent race or synchronization, and the development style is no different from synchronous. We get accelerated effortlessly, almost completely free. And there is no magic in it.
')

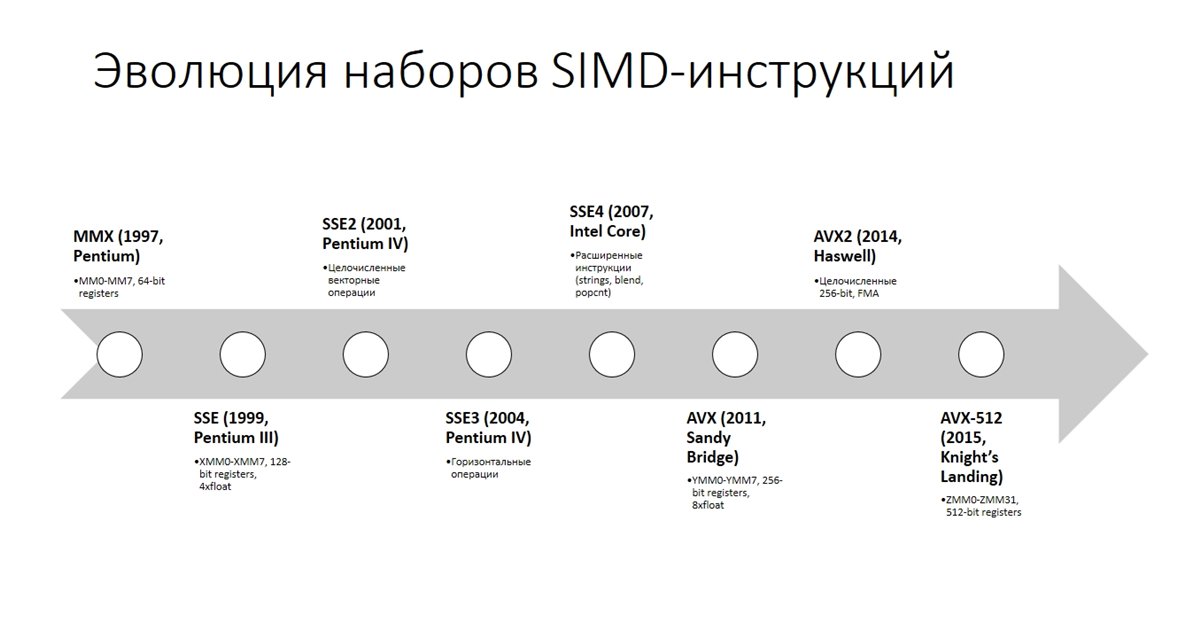
What is SSE?


SSE (English Streaming SIMD Extensions, streaming SIMD processor expansion) is SIMD (English Single Instruction, Multiple Data, One Instruction - Multiple Data) set of instructions. SSE includes eight 128-bit registers and a set of instructions in the processor architecture. SSE technology was first introduced in the Pentium III in 1999. Over time, this set of instructions has been improved by adding more complex operations. Eight (in x86-64 - sixteen) 128-bit registers were added to the processor: from xmm0 to xmm7.
image
Initially, these registers could only be used for single-precision calculations (i.e., for the type float). But after the release of SSE2, these registers can be used for any primitive data type. Given a standard 32-bit machine in this way, we can store and process in parallel:

If you use the AVX technology, then you will manipulate already 256-bit registers, respectively, more numbers for a single instruction. So there are already 512-bit registers.
image
First, using the example of C ++ (who is not interested, you can skip), we will write a program that will summarize two arrays of 8 float elements.

An example of vectorization in C ++


The SSE technology in C ++ is implemented by low-level instructions, presented in the form of pseudo-code, which reflect assembler commands. So, for example, the command __m128 _mm_add_ps (__ m128 a, __m128 b); converted to assembler instruction ADDPS operand1, operand2 . Accordingly, the command __m128 _mm_add_ss (__ m128 a, __m128 b); will be converted to an ADDSS instruction operand1, operand2 . The two teams do almost the same operations: they stack the elements of the array, but in slightly different ways. _mm_add_ps adds the entire register to the register, so that:

In this case, the entire register __m128 is the set r0-r3. But the _mm_add_ss command adds only a part of the register, so:

By the same principle, other commands are arranged, such as subtraction, division, square root, minimum, maximum, and other operations.
For writing a program, you can manipulate 128-bit registers of the type __m128 for float, __m128d for double and __m128i for int, short, char. In this case, you can not use arrays of the type __m128, but use the reduced pointers of the array float of type __m128 *.
Thus it is necessary to consider several working conditions:

Such a small excursion into the theory. However, consider an example program using SSE:
#include "iostream" #include "xmmintrin.h" int main() { const auto N = 8; alignas(16) float a[] = { 41982.0, 81.5091, 3.14, 42.666, 54776.45, 342.4556, 6756.2344, 4563.789 }; alignas(16) float b[] = { 85989.111, 156.5091, 3.14, 42.666, 1006.45, 9999.4546, 0.2344, 7893.789 }; __m128* a_simd = reinterpret_cast<__m128*>(a); __m128* b_simd = reinterpret_cast<__m128*>(b); auto size = sizeof(float); void *ptr = _aligned_malloc(N * size, 32); float* c = reinterpret_cast<float*>(ptr); for (size_t i = 0; i < N/2; i++, a_simd++, b_simd++, c += 4) _mm_store_ps(c, _mm_add_ps(*a_simd, *b_simd)); c -= N; std::cout.precision(10); for (size_t i = 0; i < N; i++) std::cout << c[i] << std::endl; _aligned_free(ptr); system("PAUSE"); return 0; }


Thus, all preparations for the SSE work are made. Further in the cycle, we summarize the elements of the arrays. The approach is based on pointer arithmetic. Since a_simd , b_simd, and c are pointers, increasing them leads to a shift to sizeof (T) from memory. If we take, for example, a dynamic array with , then with [0] and * with show the same value, since c points to the first element of the array. Incrementing with will move the pointer 4 bytes forward and now the pointer will point to 2 elements of the array. This way you can move back and forth along the array by increasing and decreasing the pointer. But at the same time, the dimension of the array should be taken into account, since it is easy to go beyond its limits and refer to someone else's memory. Working with the a_simd and b_simd pointers is similar, only the increment of the pointer will lead to a 128-bit forward and, from the point of view of the float type, 4 variables of the array a and b will be skipped. In principle, the pointer a_simd and a , like b_simd and b , respectively point to one section in memory, except for the fact that they are processed differently taking into account the pointer type dimension:
image

  for (int i = 0; i < N/2; i++, a_simd++, b_simd++, c += 4) _mm_store_ps(c, _mm_add_ps(*a_simd, *b_simd));

Now I understand why in this cycle such pointer changes. At each iteration of the cycle, 4 elements are added and the obtained result is saved to the addresses of the pointer c from the xmm0 register (for this program). Those. as we see, such an approach does not change the source data, but stores the sum in the register and, if necessary, transfers it to the operand we need. This allows you to improve the performance of the program in cases where it is necessary to reuse operands.
Consider the code that the assembler generates for the _mm_add_ps method:
 mov eax,dword ptr [b_simd] ;//   b_simd   eax(   ,   ) mov ecx,dword ptr [a_simd] ;//   a_simd   ecx movups xmm0,xmmword ptr [ecx] ;//  4       ecx   xmm0; xmm0 = {a[i], a[i+1], a[i+2], a[i+3]} addps xmm0,xmmword ptr [eax] ;//  : xmm0 = xmm0 + b_simd ;// xmm0[0] = xmm[0] + b_simd[0] ;// xmm0[1] = xmm[1] + b_simd[1] ;// xmm0[2] = xmm[2] + b_simd[2] ;// xmm0[3] = xmm[3] + b_simd[3] movaps xmmword ptr [ebp-190h],xmm0 ;//          movaps xmm0,xmmword ptr [ebp-190h] ;//    mov edx,dword ptr [c] ;//    ecx    movaps xmmword ptr [edx],xmm0 ;//      ecx      ,   (ecx)  .   xmmword       ,   _m128 - 128- ,   4

As can be seen from the code, one addps instruction processes 4 variables at once, which is implemented and supported by the hardware processor. The system does not take any part in the processing of these variables, which gives a good performance gain without extra costs from the outside.
In this case, I would like to note one feature that in this example, the compiler uses the movups instruction, for which operands are not required, which must be aligned along a 16-byte boundary. From which it follows that one could not align the array a . However, array b must be aligned, otherwise a read memory error will occur in the addps operation, because the register is added to a 128-bit memory location. In a different compiler or environment there may be other instructions, so it’s better, in any case, for all operands involved in such operations, to do alignment along the boundary. In any case, to avoid memory problems.
Another reason to do the alignment is when we operate with array elements (and not only with them), we are actually constantly working with 64-byte cache lines. SSE and AVX vectors always fall into the same cache line if they are equalized by 16 and 32 bytes, respectively. But if our data is not aligned, then it is very likely that we will have to load another “additional” cache line. This process has a strong impact on performance, and if we are at the same time and to the elements of the array, and therefore to memory, we turn inconsistently, then everything can be even worse.

SIMD support in .NET


The first mention of JIT support for SIMD technology was announced on the .NET blog in April 2014. Then the developers announced a new preview version of RyuJIT, which provided SIMD functionality. The reason for the addition was the rather high popularity of the request for support for C # and SIMD. The initial set of supported types was not large and there were limitations in functionality. Initially, the SSE suite was supported, and AVX was promised to be added in the release. Later, updates were released and new types were added with support for SIMD and new methods for working with them, which in recent versions represents an extensive and convenient library for hardware data processing.
image
This approach makes life easier for a developer who does not have to write CPU-dependent code. Instead, the CLR abstracts the hardware, providing a virtual execution environment that translates its code into machine commands either at run time (JIT) or during installation (NGEN). Leaving the CLR code generation, you can use the same MSIL code on different computers with different processors, without abandoning optimizations specific to this particular CPU.
Currently, support for this technology in .NET is represented in the System.Numerics.Vectors namespace and is a library of vector types that can take advantage of SIMD hardware acceleration. Hardware acceleration can lead to significant performance improvements in mathematical and scientific programming, as well as in graphics programming. It contains the following types:

The Vector class provides methods for addition, comparison, minimum and maximum search, and many other transformations over vectors. In this case, operations operate using SIMD technology. The remaining types also support hardware acceleration and contain transformations specific to them. For matrices, this can be multiplication, for vectors, the Euclidean distance between points, etc.

Sample C # Program


So what is needed to use this technology? You must first have RyuJIT compiler and .NET version 4.6. System.Numerics.Vectors via NuGet is not set if the version is lower. However, when the library was installed, I lowered the version and everything worked as it should. Then you need an assembly for x64, for this you need to remove in the properties of the project “prefer 32-bit platform” and can be assembled under Any CPU.
Listing:
 using System; using System.Numerics; class Program { static void Main(string[] args) { const Int32 N = 8; Single[] a = { 41982.0F, 81.5091F, 3.14F, 42.666F, 54776.45F, 342.4556F, 6756.2344F, 4563.789F }; Single[] b = { 85989.111F, 156.5091F, 3.14F, 42.666F, 1006.45F, 9999.4546F, 0.2344F, 7893.789F }; Single[] c = new Single[N]; for (int i = 0; i < N; i += Vector<Single>.Count) // Count  16  char, 4  float, 2  double  .. { var aSimd = new Vector<Single>(a, i); //     i var bSimd = new Vector<Single>(b, i); Vector<Single> cSimd = aSimd + bSimd; //   Vector<Single> c_simd = Vector.Add(b_simd, a_simd); cSimd.CopyTo(c, i); //     } for (int i = 0; i < a.Length; i++) { Console.WriteLine(c[i]); } Console.ReadKey(); } }

From a general point of view, the C ++ approach, the .NET are quite similar. It is necessary to convert / copy the source data, perform copying to the final array. However, the C # approach is much simpler, many things are done for you and you just have to use and enjoy. There is no need to think about aligning data, allocating memory and doing it statically or dynamically with certain operators. On the other hand, you have more control over what is happening with the use of pointers, but also more responsibility for what is happening.
And in the cycle everything happens as in the cycle in C ++. And I'm not talking about pointers. The algorithm for calculating the same. At the first iteration, we put the first 4 elements of the original arrays into the aSimd and bSimd structures , then summarize and save them in the final array. Then, at the next iteration, we add the next 4 elements with an offset and sum them. That's how everything is done quickly and easily. Consider the code that the compiler generates for this command var cSimd = aSimd + bSimd :
 addps xmm0,xmm1

The only difference from C ++ is that both registers are added, while there was a folding of the register with a section of memory. Register placement occurs when aSimd and bSimd are initialized . In general, this approach, when comparing the code of C ++ compilers and .NET compilers, is not very different and gives approximately equal performance. Although the option with pointers will still work faster. I would like to note that SIMD instructions are generated when code optimization is enabled. Those. see them in the disassembler in Debug does not work: it is implemented as a function call. However, in Release, where optimization is enabled, you will receive these instructions in an explicit (embedded) form.

At last


What we have:

In the course of a brief twitter correspondence with Sasha Goldstein (one of the authors of the book “Optimization of Applications on the .NET Platform”), who considered hardware acceleration in .NET, I wondered how, in his opinion, SIMD support was implemented in .NET and what compared with C ++. To which he replied: “Undoubtedly, you can do more in C ++ than in C #. But you do get cross-processor support in C #. For example, automatic selection between SSE4 and AVX. " In general, this is good news. At the cost of small efforts, we can get as much performance from the system as possible, using all possible hardware resources.
For me, this is a very good opportunity to develop productive programs. At least in my thesis work, on modeling physical processes, I basically achieved efficiency by creating a certain number of flows, as well as using heterogeneous calculations. I use both CUDA and C ++ AMP. Development is conducted on a universal platform under Windows 10, where WinRT is very appealing to me, which allows you to write a program in C # and C ++ / CX. Basically, I write a kernel for large calculations (Boost) on pluses, and in C # I already manipulate data and develop the interface. Naturally, the transfer of data through the binary interface ABI for the interaction of two languages ​​has its price (although not very large), which requires a more reasonable development of the C ++ library. However, my data is sent only if necessary and quite rarely, only to display the results.
If I need to manipulate data in C #, I will convert them to .NET types in order not to work with WinRT types, thereby increasing processing performance already in C #. For example, when you need to process several thousand or tens of thousands of elements or processing requirements have no special specifications, data can be calculated in C # without using the library (it counts from 3 to 10 million structures, sometimes only for one iteration). So the hardware accelerated approach will simplify the task and make it faster.
image

List of sources when writing an article



Well, special thanks to Sasha Goldstein for the help and information provided.

Source: https://habr.com/ru/post/274605/

More articles:


All Articles