Solving the puzzle Galakub on Python
For the new year I bought my puzzle nephew Galakub. The task is to assemble a cube of 4x4x4 size from different parts. The total amount of parts, just, 4x4x4. Before giving it was necessary to assemble a puzzle. A beautiful symmetrical solution was found quickly enough. But it became interesting only this decision or not. Intuition suggested that the only thing, but I wanted to check.

I decided to quickly sip the script to iterate through all the options. Ideally, it was necessary to catch up to Putin’s New Year’s speech. The situation was aggravated by the fact that the code was written on the MacBook of my parents. Putting some libraries on it is a bigger job than writing the program itself.
The code turned out to be surprisingly beautiful and understandable. It is convenient to explain. Maybe the text will be useful, for example, to learn Python.
All the parts were represented as 4x4x4 tensors.
')
The cube is coded with the letter “Q”, the corner is encoded with the letter “J”, and the blockhead is “Z”.
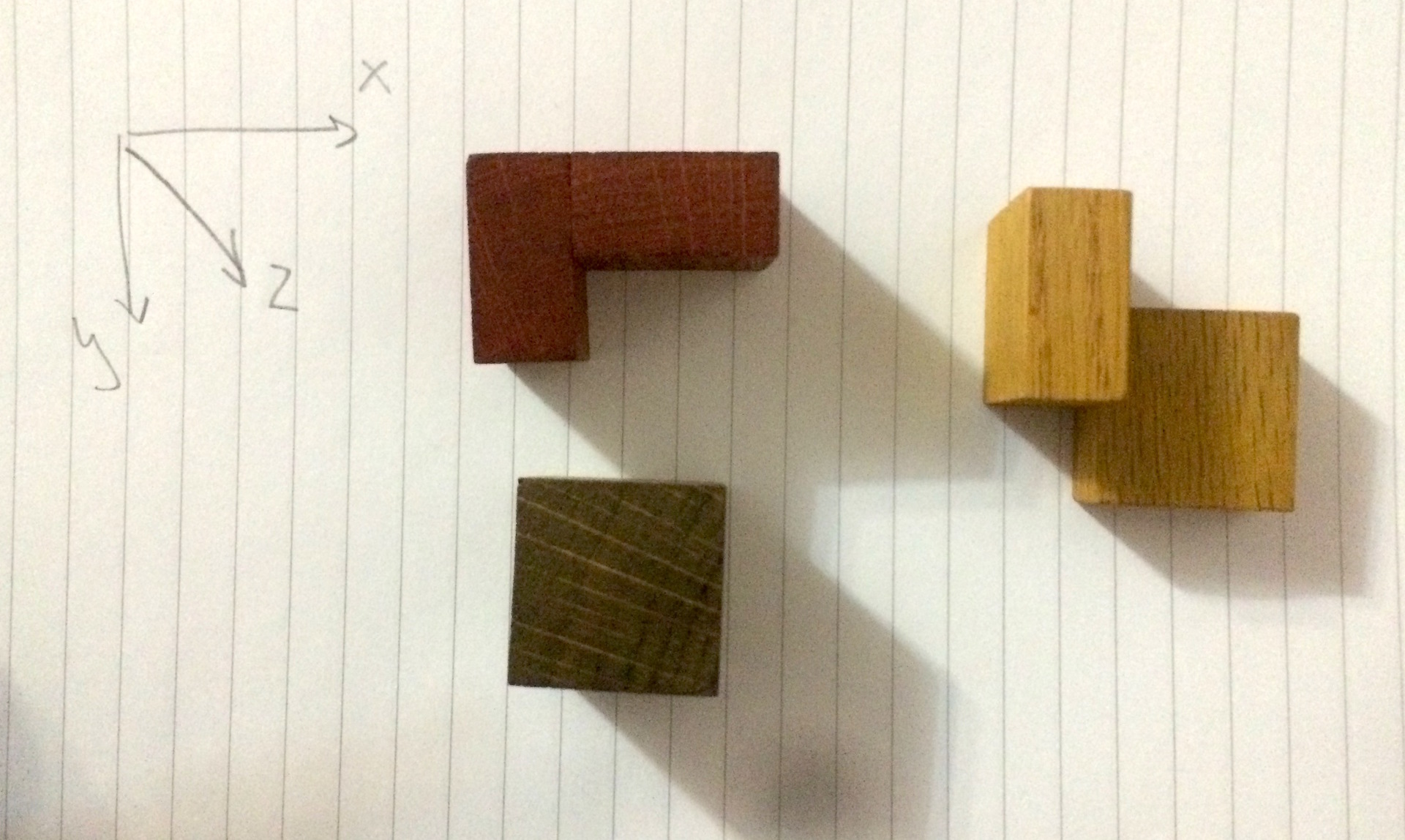
To make it easier to look at tensors (and you will need to look at them a lot and carefully), the show_tensor function of the inverse function parse_tensor was written:
Next you had to generate all possible positions for each part. Rotation along the X and Y axis by 90 degrees is reduced to a permutation of the axes.
In order not to duplicate the cycles, you can start the function transform_tensor, it will come in handy more than once:
Let's see what happens:
The rotation along the Z axis can be surprisingly obtained by rotating along the X and Y axes. You only need to rotate in different directions, so you have to enter the direction in rotate_by_y:
Let's see what happens:
Well, besides rotations, there are more shifts. With the transform_tensor function, it’s very simple to make a translation shift:
The only problem is that there are non-existent details:
Therefore, the decision will have to complicate. We will make a shift only if there is an empty space for the transfer. You need to add code to calculate the projection of the tensor and check the matrix for emptiness:
Now the shift will look like this:
Now, if the part rests on the border, nothing happens:
True, it is not possible to generate all possible details. We need to add another direction and make shifts in both directions each time. The final version is on Gitkhab.
Well, to get all possible positions for each part, you need to go through all the angles of rotation and all the dimensions of the shifts:
Many combinations are duplicated. For example, it is useless to rotate a cube, it does not add new combinations:
To leave only unique options, it is necessary to define a function that assigns a number to the tensor. To do this, you can represent the 4x4x4 tensor as a binary 64-bit number:
Now leaving unique combinations is simple:
Due to the fact that the cube is small, there are not so many options:
The most primitive search for a solution could be:
But this is too stupid, you will need to go through 288 3 432 3 27 2 options. There is an exit. After, for example, the first part is fixed, it is necessary to ignore all variants in which the second part intersects with the first one. In a head-on decision, this is not the case. Even if Z1 and Z2 overlap, all the other 6 subcycles will work. The better solution will look like this:
But there is another nuance. The tensors_intersect function looks like this:
She works for a long time. There is a way out again. The function that matches the tensor to the corresponding number was chosen very well. If we use these numbers, and not tensors, the check for intersection will look like this:
Finding solutions will change a bit:
Run:
We wait six hours and get 576 solutions. Naturally a lot of duplicate. We leave only unique and get 8 options:
Unfortunately, these are all possible rotations of the very variant that was found manually. That is, Galakub has only one solution.
I decided to quickly sip the script to iterate through all the options. Ideally, it was necessary to catch up to Putin’s New Year’s speech. The situation was aggravated by the fact that the code was written on the MacBook of my parents. Putting some libraries on it is a bigger job than writing the program itself.
The code turned out to be surprisingly beautiful and understandable. It is convenient to explain. Maybe the text will be useful, for example, to learn Python.
All the parts were represented as 4x4x4 tensors.
def zero_vector(): return [0] * 4 def zero_matrix(): return [zero_vector() for _ in xrange(4)] def zero_tensor(): return [zero_matrix() for _ in xrange(4)] ')
The cube is coded with the letter “Q”, the corner is encoded with the letter “J”, and the blockhead is “Z”.
def parse_tensor(data): tensor = zero_tensor() lines = data.splitlines() for z in xrange(2): for y in xrange(4): line = lines[z * 5 + 1 + y] for x in xrange(4): if line[x] == '*': tensor[z][y][x] = 1 return tensor J = parse_tensor(""" ***. *... .... .... ***. *... .... .... """) Q = parse_tensor(""" **.. **.. .... .... **.. **.. .... .... """) Z = parse_tensor(""" *... *... .... .... *... ***. .**. .... """) >>> J [[[1, 1, 1, 0], [1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]], [[1, 1, 1, 0], [1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]], [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]], [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]] To make it easier to look at tensors (and you will need to look at them a lot and carefully), the show_tensor function of the inverse function parse_tensor was written:
def show_tensor(tensor): for y in xrange(4): for z in xrange(4): for x in xrange(4): value = tensor[z][y][x] print { 1: '*', 0: '.' }[value], print ' ', print def show_tensors(tensors): for tensor in tensors: show_tensor(tensor) print >>> show_tensors([J, Q, Z]) * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . . . * . . . . . . . . . . . * . . . * * * . . . . . . . . . . . . . . * * . . . . . . . . . . . . . . . . . . . . . . . . . Next you had to generate all possible positions for each part. Rotation along the X and Y axis by 90 degrees is reduced to a permutation of the axes.
def rotate_by_x(tensor): rotated = zero_tensor() for z in xrange(4): for y in xrange(4): for x in xrange(4): rotated[z][y][x] = tensor[y][-z - 1][x] return rotated def rotate_by_y(tensor): rotated = zero_tensor() for z in xrange(4): for y in xrange(4): for x in xrange(4): rotated[z][y][x] = tensor[x][y][-z - 1] return rotated In order not to duplicate the cycles, you can start the function transform_tensor, it will come in handy more than once:
def transform_tensor(tensor, function): transformed = zero_tensor() for z in xrange(4): for y in xrange(4): for x in xrange(4): transformed[z][y][x] = function(tensor, x, y, z) return transformed def rotate_by_x(tensor): return transform_tensor(tensor, lambda _, x, y, z: _[y][-z - 1][x]) def rotate_by_y(tensor): return transform_tensor(tensor, lambda _, x, y, z: _[x][y][-z - 1]) Let's see what happens:
def apply_transformation(tensor, transformation, times=1): for _ in xrange(times): tensor = transformation(tensor) return tensor def show_transformation(tensor, transformation): show_tensors([ tensor, transformation(tensor), apply_transformation(tensor, transformation, times=2), apply_transformation(tensor, transformation, times=3), apply_transformation(tensor, transformation, times=4), ]) >>> show_transformation(J, rotate_by_x) * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . . . * * * . . . . . . . . . * . . . * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . . . * . . . . . . . . . . . * * * . * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * . . . . . . . . . . . * * * . * . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> show_transformation(J, rotate_by_y) * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . * * . . . . . . . . . . . . . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . * * . . . . . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . The rotation along the Z axis can be surprisingly obtained by rotating along the X and Y axes. You only need to rotate in different directions, so you have to enter the direction in rotate_by_y:
def rotate_by_y(tensor, direction=1): if direction == 1: function = lambda _, x, y, z: _[x][y][-z - 1] else: function = lambda _, x, y, z: _[-x - 1][y][z] return transform_tensor(tensor, function) def rotate_by_z(tensor): return rotate_by_y(rotate_by_x(rotate_by_y(tensor, direction=-1))) Let's see what happens:
>>> show_transformation(J, rotate_by_z) * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . . * . . . * . . . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . . . * . . . . . . . . . * * * . * * * . . . . . . . . . . . . . . . . . . . . . . . . * . . . * . . . . . . . . . . . * . . . * . . . . . . . . . . . * * . . * * . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Well, besides rotations, there are more shifts. With the transform_tensor function, it’s very simple to make a translation shift:
def shift_by_x(tensor): return transform_tensor(tensor, lambda _, x, y, z: _[z][y][(x + 1) % 4]) The only problem is that there are non-existent details:
>>> show_transformation(J, shift_by_x) * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . * * * . * . . . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . * * * . * * . . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Therefore, the decision will have to complicate. We will make a shift only if there is an empty space for the transfer. You need to add code to calculate the projection of the tensor and check the matrix for emptiness:
def project_tensor(tensor, function): projection = zero_matrix() for i in xrange(4): for j in xrange(4): projection[i][j] = function(tensor, i, j) return projection def project_by_x(tensor): return project_tensor(tensor, lambda _, z, y: tensor[z][y][0]) def project_by_y(tensor): return project_tensor(tensor, lambda _, z, x: tensor[z][0][x]) def project_by_z(tensor): return project_tensor(tensor, lambda _, y, x: tensor[0][y][x]) def is_empty_matrix(matrix): for i in xrange(4): for j in xrange(4): if matrix[i][j]: return False return True Now the shift will look like this:
def shift_by_x(tensor): if is_empty_matrix(project_by_x(tensor)): return transform_tensor(tensor, lambda _, x, y, z: _[z][y][(x + 1) % 4]) return tensor Now, if the part rests on the border, nothing happens:
>>> show_transformation(J, shift_by_x) * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . * * * . . . . . . . . . * . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . True, it is not possible to generate all possible details. We need to add another direction and make shifts in both directions each time. The final version is on Gitkhab.
Well, to get all possible positions for each part, you need to go through all the angles of rotation and all the dimensions of the shifts:
def generate_permutations(tensor): for x_rotations in xrange(4): for y_rotations in xrange(4): for z_rotations in xrange(4): for x_shifts in xrange(3): for x_direction in (-1, 1): for y_shifts in xrange(3): for y_direction in (-1, 1): for z_shifts in xrange(3): for z_direction in (-1, 1): permutation = apply_transformation(tensor, rotate_by_x, times=x_rotations) permutation = apply_transformation(permutation, rotate_by_y, times=y_rotations) permutation = apply_transformation(permutation, rotate_by_z, times=z_rotations) permutation = apply_transformation(permutation, shift_by_x, direction=x_direction, times=x_shifts) permutation = apply_transformation(permutation, shift_by_y, direction=y_direction, times=y_shifts) permutation = apply_transformation(permutation, shift_by_z, direction=z_direction, times=z_shifts) yield permutation Many combinations are duplicated. For example, it is useless to rotate a cube, it does not add new combinations:
>>> Qs = list(generate_permutations(Q)) >>> show_tensors(sample(Qs, 10)) * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . To leave only unique options, it is necessary to define a function that assigns a number to the tensor. To do this, you can represent the 4x4x4 tensor as a binary 64-bit number:
def hash_tensor(tensor): hash = 0 index = 0 for z in xrange(4): for y in xrange(4): for x in xrange(4): index += 1 hash += tensor[z][y][x] * 2 ** index return hash Now leaving unique combinations is simple:
def unique_tensors(tensors): hashes = set() for tensor in tensors: hash = hash_tensor(tensor) if hash not in hashes: yield tensor hashes.add(hash) Zs = list(unique_tensors(generate_permutations(Z))) Js = list(unique_tensors(generate_permutations(J))) Qs = list(unique_tensors(generate_permutations(Q))) >>> show_tensors(sample(Qs, 10)) . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . * * . . . . . . . . . . * * . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Due to the fact that the cube is small, there are not so many options:
>>> len(Zs), len(Js), len(Qs) (288, 432, 27) The most primitive search for a solution could be:
def solve(Zs, Js, Qs): for Z1 in Zs: for Z2 in Zs: for Z3 in Zs: for J1 in Js: for J2 in Js: for J3 in Js: for Q1 in Qs: for Q2 in Qs: if not tensors_intersect(Z1, Z2, Z3, J1, J2, J3, Q1, Q2): yield Z1, Z2, Z3, J1, J2, J3, Q1, Q2 But this is too stupid, you will need to go through 288 3 432 3 27 2 options. There is an exit. After, for example, the first part is fixed, it is necessary to ignore all variants in which the second part intersects with the first one. In a head-on decision, this is not the case. Even if Z1 and Z2 overlap, all the other 6 subcycles will work. The better solution will look like this:
def solve_(path, done, hashes, todo): for hash in hashes: if not tensors_intersect(done, hash): if todo: for solution in solve_(path + [hash], union_hashes(done, hash), todo[0], todo[1:]): yield solution else: yield path + [hash] def solve(Zs, Js, Qs): done = zero_tensor() todo = [Z_hashes] * 3 + [J_hashes] * 3 + [Q_hashes] * 2 for solution in solve_([], done, todo[0], todo[1:]): yield solution But there is another nuance. The tensors_intersect function looks like this:
def tensors_intersect(a, b): for z in xrange(4): for y in xrange(4): for x in xrange(4): if a[z][y][x] and b[z][y][x]: return True return False She works for a long time. There is a way out again. The function that matches the tensor to the corresponding number was chosen very well. If we use these numbers, and not tensors, the check for intersection will look like this:
def tensor_hashes_intersect(a, b): return a & b Finding solutions will change a bit:
def union_tensor_hashes(a, b): return a | b def unhash_tensor(hash): tensor = zero_tensor() index = 0 for z in xrange(4): for y in xrange(4): for x in xrange(4): index += 1 if hash & 2 ** index: tensor[z][y][x] = 1 return tensor def solve_(path, done, hashes, todo): for hash in hashes: if not tensor_hashes_intersect(done, hash): if todo: for solution in solve_(path + [hash], union_tensor_hashes(done, hash), todo[0], todo[1:]): yield solution else: yield path + [hash] def solve(Zs, Js, Qs): Z_hashes = [hash_tensor(_) for _ in Zs] J_hashes = [hash_tensor(_) for _ in Js] Q_hashes = [hash_tensor(_) for _ in Qs] done = hash_tensor(zero_tensor()) todo = [Z_hashes] * 3 + [J_hashes] * 3 + [Q_hashes] * 2 for solution in solve_([], done, todo[0], todo[1:]): yield [unhash_tensor(_) for _ in solution] Run:
solutions = list(solve(Zs, Js, Qs)) We wait six hours and get 576 solutions. Naturally a lot of duplicate. We leave only unique and get 8 options:
>>> show_tensors(unique_tensors(solution_tensor(_) for _ in solutions)) # # # * # * * * * * . . * * . . # # # * # * * * # * . . # * . . . . # # . . * * # * * * # * * * . . # # . . # # # # # # # # * * . . # # . . # # # # # * # # # * . . # # . . * * # * * * # * * * # # # # # * * * # * . . * * . . # # * * # * * * # * . . * * . . # # . . # # . . # # # # * * # # # # . . * * . . * * * # * * * # * # # # * * * # . . * # . . * # * # # # * * * # . . * * . . * * * * # # * * * # . . * # . . * * # # # # * * * # . . * # . . * * # # . . * * . . * * * # * * * # # # . . # # . . * # # # * # # # * * . . # * . . # * * * # # * * * * . . # * . . # * * * # # # # # * * * # * * * . . * * . . # # # # # * # # # * . . # # . . # # # # * * # # # # . . # # . . # # # * * * # * * * . . * * . . # # # * . . # * . . # * * * # # # * * * . . * * . . # * * * # # # * * # # # * # # # # # . . # # . . * * * # * * * # * * . . # # . . . . * * . . * # * * * # # # # # . . * * . . * # * * * # * * # # . . * * . . * * * * * # * # # # . . * # . . * # * * * # * # # # * * * # * * * # * * . . # # . . * * # # # # # # # # . . # # . . Unfortunately, these are all possible rotations of the very variant that was found manually. That is, Galakub has only one solution.
Source: https://habr.com/ru/post/274527/
All Articles