In English there is an abbreviation - TIFU. We cannot bring its exact value here, but you can easily find it on the web. And after the "literary processing" TIFU can be translated as "today I ruined everything." In the context of this post, this phrase refers to the use of the Math.random () function in the V8 JavaScript engine. Although it did not happen today, but a couple of years ago. Yes, and I broke the wood is not my fault, the root of evil lies in the very function.

“Many of the random number generators used today do not work very well. Developers usually try not to understand how such subroutines are arranged. And it often happens that some old, unsatisfactory working method is blindly adopted over and over again by many programmers, who often simply do not know about its inherent flaws. ”
')
Donald Knuth, The Art of Programming , volume 2.

I hope that by the end of this post you will agree with two statements:

• We were idiots because we used a pseudo-random number generator in V8 without understanding its limitations. And if it is very lazy, then it is safer to use cryptographically resistant pseudo-random number generators .
• In V8, a new implementation of Math.random () is needed. The work of the current algorithm, wandering from one programmer to another, cannot be considered satisfactory due to the weak, unobvious degradation often encountered in real projects.

I want to emphasize that the V8 engine itself is a wonderful product and its creators are very talented. I in no way blame them. Just this situation illustrates how much small nuances influence the development process.

The work of the Betable project depends on random numbers. Among other things, they are used to generate identifiers. Since the architecture is a system of distributed microservices, it was easier to implement random identifiers than sequential ones. For example, each API request generates random request identifiers . They are placed in subqueries in headers, logged and used to compare and correlate all the events taking place in all services, as a result of a single query. There is nothing difficult in generating random identifiers. Requirement one:

The probability of double generating the same identifier — the occurrence of a collision — must be extremely small . The probability of a collision is influenced by two factors:

1. The size of the identification space is the number of possible unique identifiers.
2. Method of generating identifiers - how the identifier is chosen from the common space.

Ideally, we need a large space from which uniformly distributed identifiers are randomly selected (since we assume that any “random” process uses a uniform distribution ).

We considered the probability of a collision from the paradox of birthdays and accepted that the size of the request identifier would be 22 characters long, chosen from a dictionary containing 64 letters. For example, EB5iGydiUL0h4bRu1ZyRIi or HV2ZKGVJJklN0eH35IgNaB . Since each identifier character can take one of 64 values, our identification space is 64 ²² ≈ 2 ¹³² . With this amount of space, if identifiers are randomly generated at a speed of 1 million per second , then the probability of a collision occurring within 300 years will be 1 to 6 billion .

Well, the space was big enough. How do we randomly generate? The answer is: with a decent pseudo-random generator (PRNG), which can usually be found in many standard libraries. At the top level of our stack is the Node.js service, which in turn uses the V8 engine developed by Google for Chrome. All compatible ECMAScript (JavaScript) implementations should use Math.random (), which returns a random number from 0 to 1 without any arguments. Based on the sequence of these numbers from 0 to 1, you need to generate a random word consisting of 64 characters of the alphabet. This is a fairly common task for which a standard solution has been developed:

var ALPHABET = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-_'; random_base64 = function random_base64(length) { var str = ""; for (var i=0; i < length; ++i) { var rand = Math.floor(Math.random() * ALPHABET.length); str += ALPHABET.substring(rand, rand+1); } return str; } 

Link

No need to criticize this code, everything is in order, it does exactly what it should. Go ahead. We developed a procedure for generating random identifiers with an extremely low probability of a collision. We test, commit, push, test, deploy. The above example got into production, and we forgot about it. But once a letter came from a colleague, which reported that the incredible happened:





"Anyone who allows the use of arithmetic methods to generate random numbers commits a sin." John von Neumann spoke about the obvious: the statement that deterministic methods (for example, arithmetic) cannot generate random numbers is a tautology. So what is PRNG?

What are pseudo random number generators?

Let's consider a simple PRNG and the results of its work:



This illustration explains Von Neumann’s thought: it is obvious that the generated sequence of numbers is not random. For many tasks this is quite enough. But we need an algorithm that generates numbers that seem random. Technically, they should seem independent and equally distributed random variables, evenly distributed over the entire range of the generator. In other words, we need to safely pretend that our pseudo-random numbers are truly random.

If the result of the generator is very difficult to distinguish from a truly random sequence, then it is called a high-quality generator. Otherwise - low quality . For the most part, quality is determined empirically, by running statistical tests for randomness. For example, the number of zeros and ones is estimated, the number of collisions is calculated, the Monte Carlo method is used to calculate π, etc. Another, more pragmatic method of assessing the quality of PRNG is to analyze its work in practice and compare it with true random numbers.

In addition to the non-randomness of the result, the simple algorithm we consider demonstrates other important features common to all PRNGs. If you generate numbers for a long time, sooner or later the same sequence will begin to repeat. This property is called periodicity, and all PRNGs “suffer” with it.

The period , or cycle length , is the length of the sequence of numbers created by the generator before the first repetition.

You can consider PRNG as a highly compressed codebook containing a sequence of numbers. Any spy could use it as a one-time pad. The initial position in this “book” is seed (). Gradually you will reach its end and return to the beginning, completing the cycle.

Long cycle length does not guarantee high quality, but rather contributes to it. Often it is guaranteed by some mathematical proof. Even when we cannot accurately calculate the length of the cycle, we are quite able to determine its upper limit. Since the next state of the PRNG and its result are deterministic functions of the current state, the cycle length cannot be greater than the number of possible states. To achieve the maximum length, the generator must go through all possible states before returning to the current one.

If the PRNG state is described as k-bit , then the cycle length is ≤ 2 ^k . If it really reaches this value, then such a generator is called a full-cycle generator . In good PRNGs, the cycle length is close to this upper bound. Otherwise you will waste your memory.

Let's now analyze the number of unique random values ​​generated by PRNG using some deterministic transformation of the output. Suppose we need to generate three random numbers from 0 to 15, like 2, 13, 4 or 5, 12, 15. We can have 16 ³ = 4096 such triple combinations, but the simple generator we are considering can produce only 16 combinations:



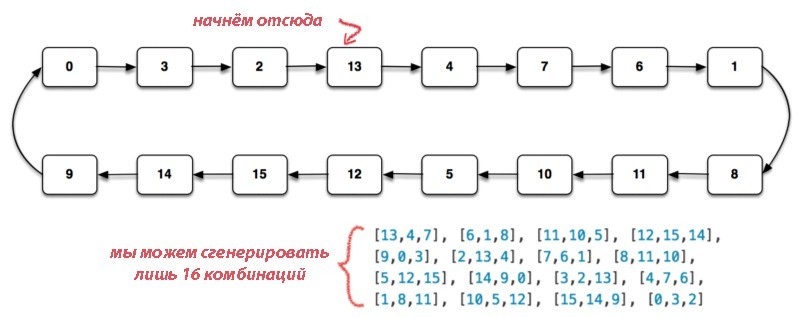
So we come to another property of all PRNGs: the number of unique values that can be generated from a pseudo-random sequence is limited by the length of the loop of the sequence .

It doesn't matter what values ​​we generate in this case. They can be 16 combinations of four values ​​(or any other length), 16 unique matrix arrays, etc. No more than 16 unique values ​​of any type.

Recall our algorithm for generating random identifiers consisting of 22 characters taken from a 64-character dictionary. It turns out that we generate combinations of 22 numbers from 0 to 63. And here we are confronted with the same problem: the number of possible unique identifiers is limited by the size of the internal state of the PRNG and the length of its cycle.

Math.random ()

Let's return to our sheep. Having received a letter about the occurrence of a collision, we quickly revised our mathematical calculations on the paradox of birthdays and checked the code. Nothing criminal was found, which means that the problem lies deeper. Began to understand.

Here is what Math.random () says in the ECMAScript specification :

Returns a positive numeric value greater than or equal to 0 but less than 1, chosen randomly or pseudo-randomly with an approximately uniform distribution in this range, using an algorithm or strategy that is implementation-specific.

Specification is poor. Firstly, nothing is said about accuracy. Since ECMAScript uses IEEE 754 binary64 double-precision floating-point numbers, we can expect an accuracy of 53 bits (that is, random values ​​take the form x / 2 ⁵³ , where x = 0 ... 2 ⁵³ - 1). Mozilla’s SpiderMonkey engine is of the same opinion , but it’s not. As will be shown below, the accuracy of Math.random () in V8 is only 32 bits (values ​​take the form x / 2 ³² , where x = 0 ... 2 ³² - 1). However, this is not important, since we need six bits to generate random letters from our dictionary.

But what turned out to be really important for us is that the specification does not define a specific algorithm. There are no requirements for the minimum cycle length, so goodbye, quality: the distribution should only be "approximately uniform." So, to find the cause of the collision, you need to analyze the specific algorithm used by the V8. We didn't find anything in the documentation, so we had to access the source code.

Pseudo-random number generator in V8

"I had to put up with the whirlwind of Mersenne , because it is used by everyone (Python, Ruby, etc.)." This brief description of Dina McNami is the only informative review on the analysis of the PRNG code in V8, when it was first committed on June 15, 2009.

Over the past six years, the PRNG code in the V8 has been reworked and aligned. Previously, it was a native code , and now it is in user space . But the algorithm remained unchanged. The current implementation uses an internal API and is rather confusing, so consider a more readable implementation of the same algorithm:

 var MAX_RAND = Math.pow(2, 32); var state = [seed(), seed()]; var mwc1616 = function mwc1616() { var r0 = (18030 * (state[0] & 0xFFFF)) + (state[0] >>> 16) | 0; var r1 = (36969 * (state[1] & 0xFFFF)) + (state[1] >>> 16) | 0; state = [r0, r1]; var x = ((r0 << 16) + (r1 & 0xFFFF)) | 0; if (x < 0) { x = x + MAX_RAND; } return x / MAX_RAND; } 

Link.

It looks obscure, we will understand.

There is one clue. In older versions of the V8, there was a comment: "The random number generator uses the MWC algorithm of George Marsaglia." In the search engine found the following:

• George Marsalya was a mathematician, most of his career was engaged in the study of PRNG. He also developed Diehard tests to measure the quality of random number generators.
• MWC means multiply-wit-carry . This is a class of pseudo-random number generators developed by Marsalya . They are very similar to the classical linear congruential generators (LCG), an example of which we considered above. And if you believe paragraph 3.6 of this document , the MWC is fully consistent with the LCG. The only difference is that MWCs can generate sequences with a longer cycle length with a comparable number of processor cycles.

So if you need a PRNG, then the MWC seems like a good choice.

But the algorithm implemented in V8 is unlike the typical MWC. Probably, the reason is that this is not MWC, but two MWC generators at once - one in line 5, the second in line 6 - jointly generating one random number in line 9. I will not spread all the calculations here, but each of these subgenerators has a cycle length of approximately 2 ³⁰ , which gives a total length of the generated sequence of approximately 2 ⁶⁰ .

But we have, as you remember, ^2,132 possible identifiers. Assume that the condition of uniform distribution. Then the probability of a collision after randomly generated 100 million identifiers should be less than 0.4%. But collisions began to occur much earlier. Probably, we were mistaken somewhere with our analysis. Perhaps the problem lies in the uniform distribution - there is probably some additional structure in the generated sequence.

The story of two generators

Let's look again at the identifier generation code:

 var ALPHABET = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-_'; random_base64 = function random_base64(length) { var str = ""; for (var i=0; i < length; ++i) { var rand = Math.floor(Math.random() * ALPHABET.length); str += ALPHABET.substring(rand, rand+1); } return str; } 

Link

Of great importance is the scaling method in the sixth row. It is recommended by MDN for scaling random numbers and is used very widely ( example 1 , example 2 , example 3 , example 4 , example 5 , example 6 ). The method is known as multiply-and-floor, take-from-top . He received the last name because the lower bits of the random number are cut off, and the left bits - the top, top, - are used as a scaled integer result.

Note: if the ratio of the output range of the PRNG to the scalable range is a fractional number, then this method works with a small offset (biased). This is usually solved by using the deviation sample used in standard libraries of other languages .



Notice what the problem is? Two generators are rather strangely mixed in the V8 algorithm. Numbers from two streams are not combined modulo 2 (xor). Instead, the lower 16 bits of the output of each subgenerator are simply concatenated. That seems to be the problem. When we multiply Math.random () by 64 and bring it to the smallest one (floor), then we will have the upper 6 bits. These bits are generated exclusively by one of the two MWC generators.



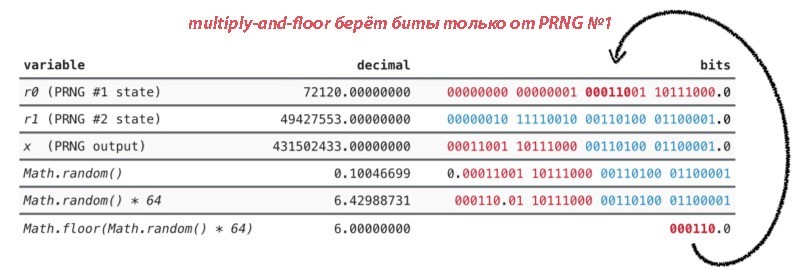
Bits from PRNG No. 1 are highlighted in red, and PRNG No. 2 from blue.

If we independently analyze the first generator, then we will see that its internal state is 32 bits long. This is not a full cycle generator, the actual length is about 590 million: 18.030 * 2 ¹⁵ - 1, the details of the calculations can be found here - link 1 , link 2 . That is, we can generate no more than 590 million unique identifiers of the request. And if they were chosen randomly, then after 30 thousand generations the probability of a collision would be 50% .

But if this were so, we would almost immediately begin to notice collisions. But we did not notice them. To understand why this did not happen, let's recall the example of generating combinations of three numbers using 4-bit LCG.



In this case, the paradox of birthdays is not applicable - the sequence cannot even be called a random sequence, so we cannot pretend . Obviously, there will be no duplicates before the 17th combination. The same thing happens with PRNG in V8: under certain conditions, the lack of randomness reduces the likelihood that we will see a collision.

That is, the determinism of the generator has played into our hands. But this is not always the case. The main conclusion we made is that even in a high-quality PRNG, it is impossible to assume the randomness of the distribution if the cycle length is not much more than the number of values ​​generated by you.

If you need N random values, then you need to use PRNG with a cycle length of at least N ² . The reason for this is that, given the period of PRNG, excessive uniformity can reduce performance in some important statistical tests (especially in tests for the presence of collisions). To prevent this from happening, the sample size N must be proportional to the square root of the period length. You can read more about this on page 22 of the wonderful work of Pierre Lecuyet, in the chapter on random number generators.

In cases like ours, when they are trying to generate unique values ​​using several independent sequences from one generator, they are concerned not so much about randomness, but about the fact that the sequences do not match. Suppose we have N sequences with length L from a generator with period P. Then the probability of coincidence will be equal to



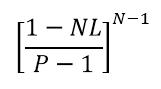
For sufficiently large values ​​of P, the probability will be approximately equal to LN ² / P (details: link 1 , link 2 ). So, we need a long cycle, otherwise we will erroneously pretend that our sequence is random.

In short, if you use Math.random () in V8 and you need a sufficiently high-quality sequence of random numbers, then do not use more than 24 thousand numbers. And if you generate in several powerful threads and you need to avoid coincidences, then generally forget about Math.random ().

Brief history MWC1616

“The MWC generator concatenates two 16-bit multiply-with-carry-generator [...] has a period of 2 ⁶⁰ and seems to pass all tests for randomness. The favorite individual generator is faster than the KISS containing it. ” This is an excerpt from the MWC1616 algorithm description underlying Math.random () in V8. Judging by the words of Marsaly, it satisfies most of the main criteria by which PRNG is chosen.

The MWC1616 was introduced in 1997 as a simple main generator. The phrase "it seems to pass all tests for randomness" gives the empiricality of the Marsala methodology. He seems to have trusted the algorithm since he passed the Diehard tests. Unfortunately, the tests that he used in the late 1990s were not good enough, at least based on modern standards. If you run the MWC1616 through a more modern testing framework like TestU01 , the result will be disastrous . Even the MINSTD generator shows better results, but it became outdated in the 1990s. Probably, Diehard's tests were simply not detailed enough, so Marsalla made such a conclusion.

 // January 12, 1999 / V8 PRNG: ((r0 << 16) + (r1 ^ 0xFFFF)) % 2^32 var x = ((r0 << 16) + (r1 & 0xFFFF)) | 0; // January 20, 1999: (r0 << 16) + r1) % 2^32 var x = ((r0 << 16) + r1) | 0; 

Link

As far as I know, the concatenation procedure for two subsets of the generated bits, performed in MWC1616, has no mathematical basis. Usually, bits from subgenerators are combined using modulo arithmetic (for example, xor). It seems that Marsalla attended to the lack of a mathematical basis soon after the publication of his algorithm as a component of one of the versions of the KISS generator . January 12, 1999 released version MWC1616, used in the V8. And on January 20, Marsala published another version of his algorithm. In it, the upper bits of the second generator are not discarded, the streams are mixed more precisely.

Both versions of the algorithm appeared on different resources, which caused confusion. A later (improved) version called MWC with Base b = 2 ¹⁶ is published on Numerical Recipes under the heading "When You Have Only 32-Bit Computing." And instead of introducing one of the algorithms, it was suggested “to use a better compiler!”. Pretty dull advice with regards to the algorithm that is better used in V8. For an inexplicable reason, the version of January 20 is given in Wikipedia as an example of a computational method for generating random numbers. The older version of January 12th was included twice in TestU01 , first under the name MWC1616, and then MWC97R. Also, this algorithm is used as one of the generators in the R language .

In general, MWC is used quite widely. And I hope this article will serve as a warning to many developers, becoming the development and confirmation of Knut’s observations:

• In general, you need to independently analyze the work of PRNG in order to understand the limitations of the algorithms used or implemented.
• Do not use MWC1616, it is of little use to it.

There are many more useful options. Let's look at a couple.

CSPRNG Alternative

So, we had to quickly replace Math.random () with something. There are many other PRNGs for JavaScript, but we had two conditions:

• The generator must have a sufficiently long period to generate ^2,132 identifiers.
• It should be thoroughly tested and have good support.

Fortunately, the standard library Node.js has another generator that meets our requirements: crypto.randomBytes () , a cryptographically secure PRNG (CSPRNG) that calls RAND_bytes , used in OpenSSL. According to the documents , it issues a random number using the SHA-1 hash with an internal state of 8184 bits, which is regularly re-randomized (reseed) from various entropic sources. In a web browser, crypto.getRandomValues ​​() should do the same .

This solution has three drawbacks:

• CSPRNG almost always uses non-linear transformations, and therefore they run slower than non-cryptographic alternatives.
• Many CSPRNG systems cannot be randomized (seed), which makes it impossible to create a reproducible sequence (for example, for testing purposes).
• CSPRNG may unpredictably stand out against all other quality measures, some of which may be more important for your project.

However, there are advantages:

• In most cases, CSPRNG's performance is quite enough (on my machine, I can get about 100 MB / s of random data in Chrome using crypto.getRandomValues ​​()).
• . , , , .
• « », , .

, - . , CSPRNG. , , . CSPRNG ( ), urandom , ( Linux , OpenSSl, OS X — Yarrow ).

, crypto.randomBytes(). , . , . OpenSSL / , ? Math.random() crypto.randomBytes(), .

Chrome Math.random() CSPRNG, crypto.randomBytes(). , WebKit . .

PRNG V8

, Math.random() V8 , . , . , :





— Safari, — V8. :



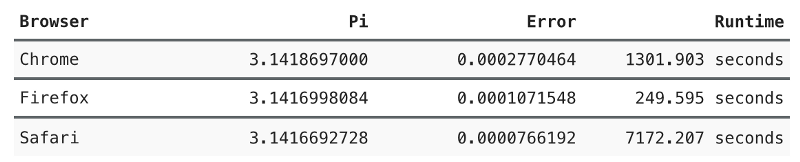
π -, 10 ¹⁰ . .

, , Math.random() - . — . , MWC1616. .

. , :

• (seed) — , 1024 . . 99,9% 2 ¹⁰²⁴ , .
• Speed — 25 .
• . , 1024 JavaScript 256 ( 32 64- ). , , , .
• . — , 2 ⁵⁰ , . 2 ¹⁰⁰ 2 ⁵⁰ , .
• . — TestU01 . , Dieharder . BigCrush . NIST rngtest , .

PRNG, . xorshift ( ) . , xorgens4096, JavaScript . 4096 , 2 ⁴⁰⁹⁶ Chrome , MWC1616. , BigCrush.

, xorshift- , BigCrush. xorshift*. , . xorshift1024* , . Xorshift64* , , MWC1616. - — PCG — .

, . , , . MT19937, 1990-. . , . , . 2 ¹⁹⁹³⁷ – 1, 2 . JavaScript . Math.random() Chrome .

, - . , . — . MWC1616, !

Results

. :

• V8 Math.random() MWC1616. 16 , ( 2 ³⁰ ). . , . .
• , PRNG. ( ) — urandom . crypto.getRandomValues() .
• , , MWC1616. V8 . , , — (MT19937).

, Mozilla LCG- Java- util.Random , MWC1616. SpiderMonkey.

. Take care of yourself!