Chaos generators on FPGA
Hello!
This article is dedicated to amazing features in the world of chaos. I will try to talk about how to curb such a strange and complex thing as a chaotic process and learn how to create your own simplest chaos generators. Together with you we will go from dry theory to beautiful visualization of chaotic processes in space. In particular, using the example of well-known chaotic attractors, I will show how to create dynamic systems and use them in problems related to programmable logic integrated circuits (FPGAs).

Chaos theory is an unusual and young science that describes the behavior of nonlinear dynamical systems. In the process of its inception, the theory of chaos simply turned over modern science! It excited the minds of scientists and forced them to dive more and more into the study of chaos and its properties. Unlike noise, which is a random process, chaos is deterministic. That is, for chaos, there is a law of variation of the quantities included in the equations describing a chaotic process. It would seem that with this definition, chaos is no different from any other vibrations described as a function. But it is not. Chaotic systems are very sensitive to the initial conditions, and their slightest changes can lead to enormous differences. These differences can be so strong that it will be impossible to tell if one or more systems have been investigated. From popular science sources, this property of chaos describes a process called the " butterfly effect " best of all. Many have heard of him, and even read books and watched films that used a trick using the butterfly effect. In essence, the butterfly effect reflects the main property of chaos.
')
The American scientist Edward Lorenz, one of the pioneers in the field of chaos, once said:

So, let's plunge into the theory of chaos and see what means can be used to generate chaos.
Before setting out the main material, I would like to give a few definitions that will help to understand and clarify some points in the article.
A dynamic system is a set of elements for which a functional dependence is set between the time coordinate and the position in the phase space of each element of the system. Simply put, a dynamic system is one in which the state in space changes over time.
Many physical processes in nature are described by systems of equations, which are dynamic systems. For example, these include combustion processes, the flow of liquids and gases, the behavior of magnetic fields and electrical oscillations, chemical reactions, meteorological phenomena, changes in populations in plants and animals, turbulence in sea currents, the movement of planets and even galaxies. As you can see, many physical phenomena can be described to some extent as a chaotic process.
A phase portrait is a coordinate plane in which each point corresponds to the state of a dynamic system at a certain point in time. In other words, it is a spatial model of the system (it can be two-dimensional, three-dimensional, and even four-dimensional or more).
An attractor is a set of the phase space of a dynamical system for which all trajectories over time attract themselves to this set. If it is a very simple language, then this is some area in which the behavior of the system in space is concentrated. Many chaotic processes are attractors, since they are concentrated in a certain area of space.
In this article I would like to talk about the four main attractors - Lorenz, Ressler, Rikitake and Nose-Hoover. In addition to the theoretical description, the article reflects aspects on the creation of dynamic systems in the MATLAB Simulink environment and their further integration into the Xilinx FPGA using the System Generator tool. Why not VHDL / Verilog? Attractors can be synthesized using RTL languages, but for a better visualization of all processes, MATLAB is an ideal option. I will not touch upon the difficult moments associated with the calculation of the spectrum of Lyapunov exponents or the construction of Poincare sections. And even more, there will be no bulky mathematical formulas and conclusions. So let's get started.
To create chaos generators, we need the following software:
These programs are quite heavy, so be patient when installing them. It is better to start the installation with MATLAB, and then install the Xilinx software (with a different sequence, some of my friends could not integrate one application into another). When you install the latter pops up a window where you can link Simulink and System Generator. There is nothing complicated and unusual in the installation, so we omit this process.
The Lorenz attractor is perhaps the most famous dynamical system in chaos theory. For several decades, it has attracted the attention of many researchers to describe certain physical processes. The first mention of the attractor is given in 1963 in the works of E. Lorentz, who was engaged in modeling atmospheric phenomena. The Lorenz attractor is a three-dimensional dynamic system of nonlinear autonomous differential equations of the first order. It has a complex topological structure, is asymptotically stable and Lyapunov stable. The Lorenz attractor is described by the following system of differential equations:

In the formula, the point above the parameter means taking the derivative, which reflects the rate of change of the value over time (the physical meaning of the derivative).
For the values of the parameters σ = 10, r = 28 and b = 8/3, this simple dynamic system was obtained by E. Lorentz. For a long time he could not understand what was happening with his computer, until he finally realized that the system was showing chaotic properties! It was obtained in the course of experiments for the problem of modeling fluid convection. In addition, this dynamic system describes the behavior of the following physical processes:
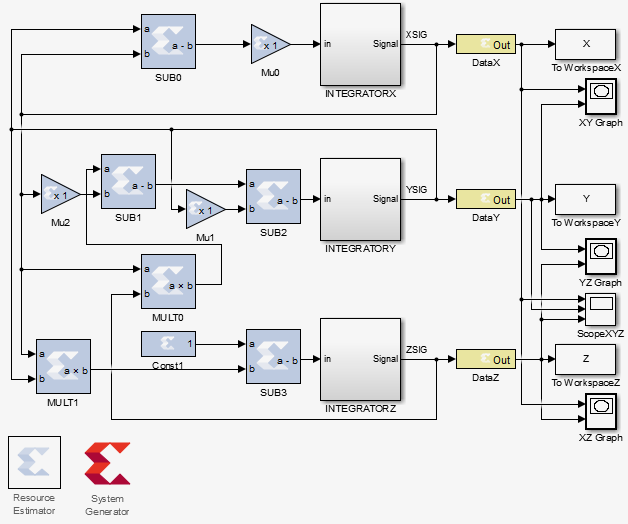
The following figure shows the Lorenz attractor system in MATLAB:
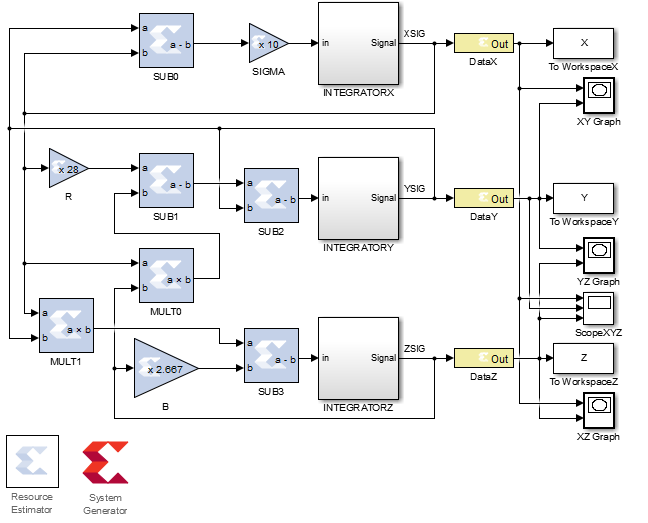
The figure uses the following notation:
In addition, the diagram shows auxiliary analysis tools, these are:
Inside each node of mathematical operations, you must specify the width of the intermediate data and their type. Unfortunately, in FPGA it is not so easy to work with a floating point and in most cases all operations are performed in a fixed-point format. Incorrect setting of parameters can lead to incorrect results and upset you when building your systems. I experimented with different values, but stopped at the following data type: 32-bit vector of signed numbers in a fixed-point format. 12 bits are allocated to the integer part, 20 bits per fractional part.
Having installed the integrator X, Y, Z in the trigger block the initial value of the system, for example, {10, 0, 0} , I launched the model. In the time base, the following three signals can be observed:
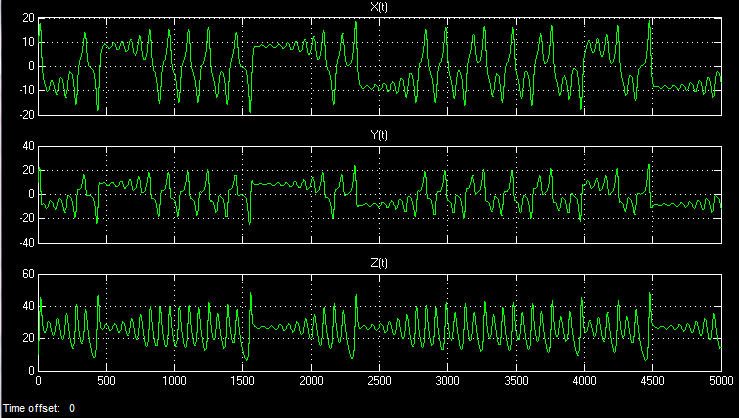
Even if the simulation time is directed to infinity, the realization in time will never be repeated. Chaotic processes are non-periodic.
In three-dimensional space, the Lorenz attractor looks like this:

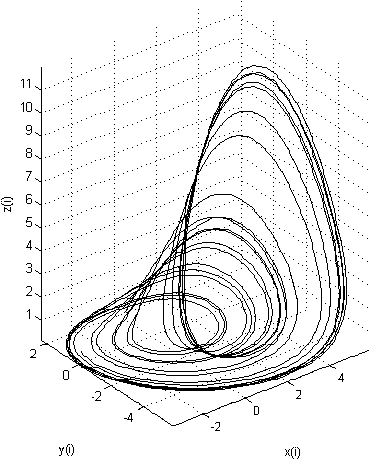
It is seen that the attractor has two points of attraction, around which the whole process occurs. With a slight change in the initial conditions, the process will also be concentrated around these points, but its trajectories will differ significantly from the previous version.
The second by the number of references in scientific articles and publications is an attractor. For the Rössler attractor , the presence of a boundary point for the manifestation of chaotic or periodic properties is characteristic. At certain parameters of the dynamic system, the oscillations cease to be periodic, and chaotic oscillations arise. One of the remarkable properties of the Rössler attractor is the fractal structure in the phase plane, that is, the self-similarity phenomenon. You can see that the other attractors, as a rule, have this property.
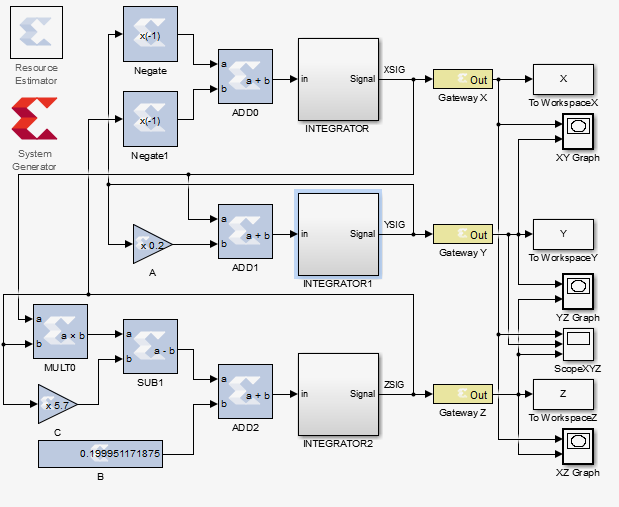
The Rossler attractor is observed in many systems. For example, it is used to describe fluid flows, as well as to describe the behavior of various chemical reactions and molecular processes. The Rössler system is described by the following differential equations:
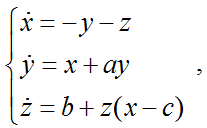
In the MATLAB environment, the attractor is constructed as follows:
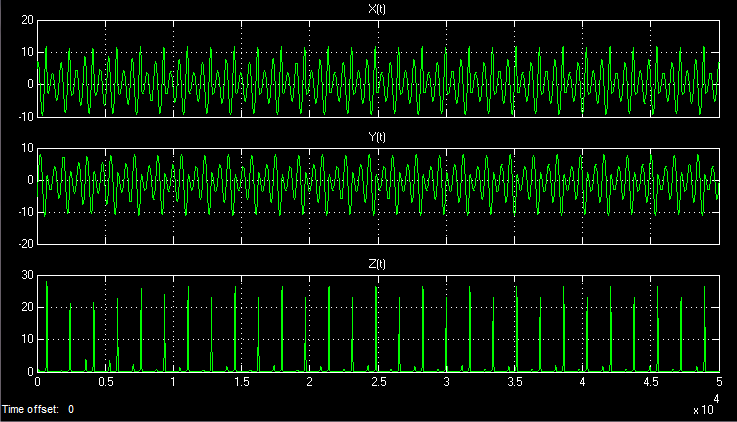
Temporal realization of spatial values:
Three-dimensional model of the Roessler attractor:
Compare pictures of three-dimensional attractors under different initial conditions and coefficients in the system of equations. See how dramatically the trajectories of movement in the first case? But one way or another they are concentrated near a single region of attraction. In the second case, the attractor in general ceased to show signs of chaos, turning into a closed periodic loop (limit cycle).
Dynamo Rikitake is one of the known third-order dynamical systems with chaotic behavior. It is a model of a two-disk dynamo and was first proposed in problems of the chaotic inversion of the geomagnetic field of the Earth. The scientist Rikitake investigated a dynamo system with two interconnected disks constructed in such a way that the current from one disk coil flowed into another and excited the second disk, and vice versa. At some point, the system began to crash and show unpredictable things. Active studies of the attractor allowed the Rikitake dynamo to be projected onto the coupling model of large magnetic field vortices in the core of the Earth.
Dynamo Rikitake is described by the following system of equations:

Model Dynamo Rikitake in MATLAB:
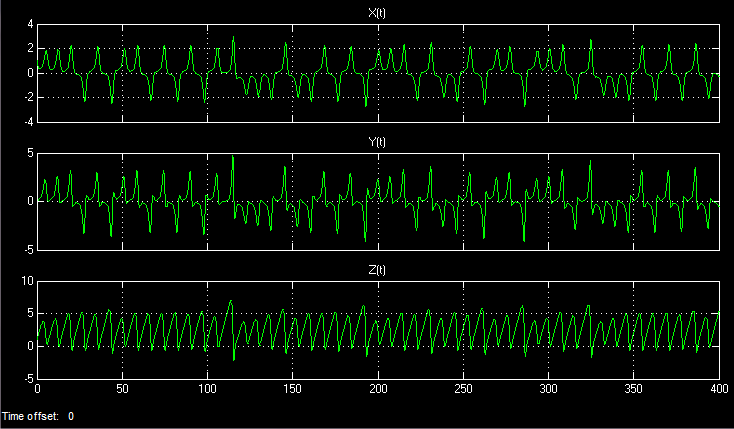
Temporary implementation:
Attractor (first version):

You may notice that the Rikitake dynamo is somewhat similar to the Lorenz attractor, but these are completely different systems and describe different physical processes!
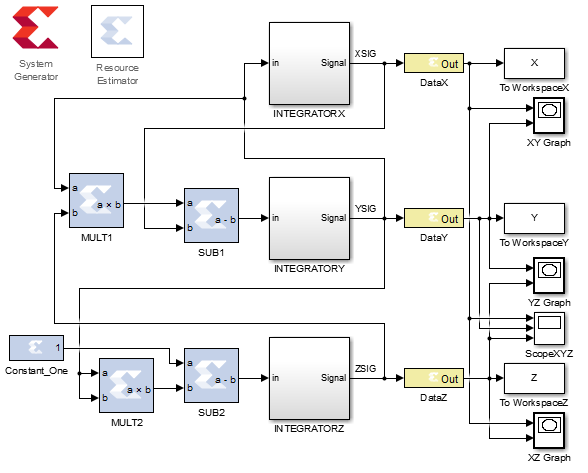
A less famous, but no less important, three-dimensional dynamic system is the Nose-Hoover thermostat . Used in molecular theory as a reversible in time thermostatic system. Unfortunately, I don’t know so much about this attractor as about the others, but I found it interesting and I included it in the review.
The Nose-Hoover thermostat is described by the following system of equations:
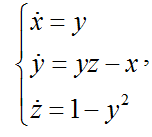
Nose Hoover model in MATLAB:
Temporary implementation:

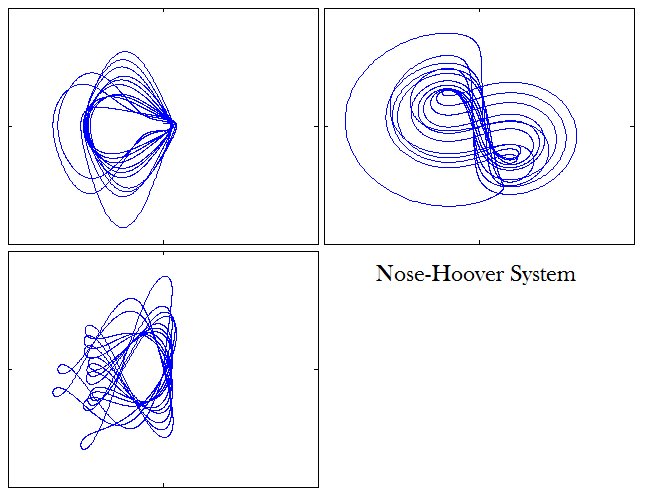
Two-dimensional projections of the attractor:
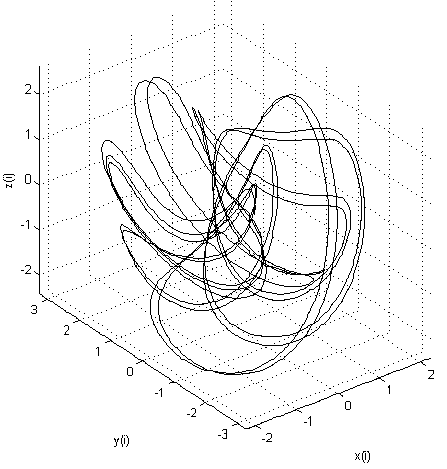
Three-dimensional model of the Nose-Hoover thermostat:
To synthesize the project, you need to click on the red “X” icon, which will launch the System Generator settings. Here you can select the FPGA family and type, the resulting file format (VHDL / Verilog - for creating source codes, NGC - for creating a kernel in the form of a list of connections), preliminary clock frequencies, etc. My typical settings are shown in the following figure:

After installing all the settings - click "Generate" and at the output we have a synthesized project for the FPGA. Then it’s easy to insert the generated kernel into the part of the project you need. (How this is done, you can find in my other articles on digital signal processing). All listed attractors occupy very few resources in modern FPGA crystals (about 10-20 DSP48 blocks and a bit of logic).
These attractors are used in many physical processes in various fields of science and technology - from physics and chemistry to mechanics and meteorology. In particular, chaos generators are used to create long sequences of pseudo-random numbers (PRS). In the tasks of radio engineering, chaos can be used to modulate a carrier when creating ultra-wideband signals by digital methods (on FPGAs or processors).
Chaos theory is an interesting and amazing science. And thanks to modern analysis and modeling tools, it becomes quite attractive for research. With the help of this article you can independently model your own dynamical systems, up to hyperchaotic systems of order higher than 3 (for example, Lorentz hyperhaos, Rossler, etc.). I hope, the material of my publication can be useful to someone, and someone will find something new and useful for themselves.
Attractor source files on Github
My articles on similar topics:
Hooray, the Hub FPGA is back for Habr. Happy New Year, everyone!
This article is dedicated to amazing features in the world of chaos. I will try to talk about how to curb such a strange and complex thing as a chaotic process and learn how to create your own simplest chaos generators. Together with you we will go from dry theory to beautiful visualization of chaotic processes in space. In particular, using the example of well-known chaotic attractors, I will show how to create dynamic systems and use them in problems related to programmable logic integrated circuits (FPGAs).

Introduction
Chaos theory is an unusual and young science that describes the behavior of nonlinear dynamical systems. In the process of its inception, the theory of chaos simply turned over modern science! It excited the minds of scientists and forced them to dive more and more into the study of chaos and its properties. Unlike noise, which is a random process, chaos is deterministic. That is, for chaos, there is a law of variation of the quantities included in the equations describing a chaotic process. It would seem that with this definition, chaos is no different from any other vibrations described as a function. But it is not. Chaotic systems are very sensitive to the initial conditions, and their slightest changes can lead to enormous differences. These differences can be so strong that it will be impossible to tell if one or more systems have been investigated. From popular science sources, this property of chaos describes a process called the " butterfly effect " best of all. Many have heard of him, and even read books and watched films that used a trick using the butterfly effect. In essence, the butterfly effect reflects the main property of chaos.
')
The American scientist Edward Lorenz, one of the pioneers in the field of chaos, once said:
A butterfly flapping in Iowa can cause an avalanche of effects that can culminate in the rainy season in Indonesia.

So, let's plunge into the theory of chaos and see what means can be used to generate chaos.
Theory
Before setting out the main material, I would like to give a few definitions that will help to understand and clarify some points in the article.
A dynamic system is a set of elements for which a functional dependence is set between the time coordinate and the position in the phase space of each element of the system. Simply put, a dynamic system is one in which the state in space changes over time.
Many physical processes in nature are described by systems of equations, which are dynamic systems. For example, these include combustion processes, the flow of liquids and gases, the behavior of magnetic fields and electrical oscillations, chemical reactions, meteorological phenomena, changes in populations in plants and animals, turbulence in sea currents, the movement of planets and even galaxies. As you can see, many physical phenomena can be described to some extent as a chaotic process.
A phase portrait is a coordinate plane in which each point corresponds to the state of a dynamic system at a certain point in time. In other words, it is a spatial model of the system (it can be two-dimensional, three-dimensional, and even four-dimensional or more).
An attractor is a set of the phase space of a dynamical system for which all trajectories over time attract themselves to this set. If it is a very simple language, then this is some area in which the behavior of the system in space is concentrated. Many chaotic processes are attractors, since they are concentrated in a certain area of space.
Implementation
In this article I would like to talk about the four main attractors - Lorenz, Ressler, Rikitake and Nose-Hoover. In addition to the theoretical description, the article reflects aspects on the creation of dynamic systems in the MATLAB Simulink environment and their further integration into the Xilinx FPGA using the System Generator tool. Why not VHDL / Verilog? Attractors can be synthesized using RTL languages, but for a better visualization of all processes, MATLAB is an ideal option. I will not touch upon the difficult moments associated with the calculation of the spectrum of Lyapunov exponents or the construction of Poincare sections. And even more, there will be no bulky mathematical formulas and conclusions. So let's get started.
To create chaos generators, we need the following software:
- MATLAB R2014 with a license for Simulink and DSP Toolbox.
- Xilinx ISE Design Suite 14.7 with a license for System-Generator (DSP Edition)
These programs are quite heavy, so be patient when installing them. It is better to start the installation with MATLAB, and then install the Xilinx software (with a different sequence, some of my friends could not integrate one application into another). When you install the latter pops up a window where you can link Simulink and System Generator. There is nothing complicated and unusual in the installation, so we omit this process.
Lorenz attractor
The Lorenz attractor is perhaps the most famous dynamical system in chaos theory. For several decades, it has attracted the attention of many researchers to describe certain physical processes. The first mention of the attractor is given in 1963 in the works of E. Lorentz, who was engaged in modeling atmospheric phenomena. The Lorenz attractor is a three-dimensional dynamic system of nonlinear autonomous differential equations of the first order. It has a complex topological structure, is asymptotically stable and Lyapunov stable. The Lorenz attractor is described by the following system of differential equations:

In the formula, the point above the parameter means taking the derivative, which reflects the rate of change of the value over time (the physical meaning of the derivative).
For the values of the parameters σ = 10, r = 28 and b = 8/3, this simple dynamic system was obtained by E. Lorentz. For a long time he could not understand what was happening with his computer, until he finally realized that the system was showing chaotic properties! It was obtained in the course of experiments for the problem of modeling fluid convection. In addition, this dynamic system describes the behavior of the following physical processes:
- - model of the single-mode laser,
- - convection in a closed loop and a flat layer,
- - rotation of the water wheel,
- - harmonic oscillator with inertial nonlinearity,
- - turbulence of cloud masses, etc.
The following figure shows the Lorenz attractor system in MATLAB:

The figure uses the following notation:
- subtracters: SUB0-3 ;
- multipliers per constant: SIGMA, B, R ;
- multipliers: MULT0-1 ;
- integrators with a cell specifying the initial condition: INTEGRATOR X, Y, Z ;
- output ports OUT: DATA X, Y, Z for signals XSIG, YSIG, ZSIG ;
In addition, the diagram shows auxiliary analysis tools, these are:
- saving calculation results to file: To Workspace X, Y, Z ;
- spatial graphing: Graph XY, YZ, XZ ;
- plotting timelines: Scope XYZ ;
- tools for estimating occupied crystal resources and generating HDL code from the Resource Estimator and System Generator models.
Inside each node of mathematical operations, you must specify the width of the intermediate data and their type. Unfortunately, in FPGA it is not so easy to work with a floating point and in most cases all operations are performed in a fixed-point format. Incorrect setting of parameters can lead to incorrect results and upset you when building your systems. I experimented with different values, but stopped at the following data type: 32-bit vector of signed numbers in a fixed-point format. 12 bits are allocated to the integer part, 20 bits per fractional part.
Having installed the integrator X, Y, Z in the trigger block the initial value of the system, for example, {10, 0, 0} , I launched the model. In the time base, the following three signals can be observed:

Even if the simulation time is directed to infinity, the realization in time will never be repeated. Chaotic processes are non-periodic.
In three-dimensional space, the Lorenz attractor looks like this:

It is seen that the attractor has two points of attraction, around which the whole process occurs. With a slight change in the initial conditions, the process will also be concentrated around these points, but its trajectories will differ significantly from the previous version.
Rössler Attractor
The second by the number of references in scientific articles and publications is an attractor. For the Rössler attractor , the presence of a boundary point for the manifestation of chaotic or periodic properties is characteristic. At certain parameters of the dynamic system, the oscillations cease to be periodic, and chaotic oscillations arise. One of the remarkable properties of the Rössler attractor is the fractal structure in the phase plane, that is, the self-similarity phenomenon. You can see that the other attractors, as a rule, have this property.
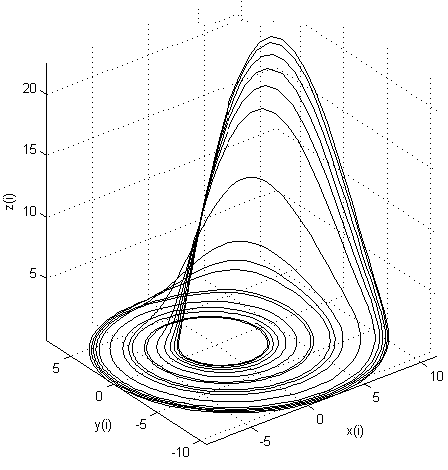
The Rossler attractor is observed in many systems. For example, it is used to describe fluid flows, as well as to describe the behavior of various chemical reactions and molecular processes. The Rössler system is described by the following differential equations:
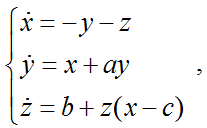
In the MATLAB environment, the attractor is constructed as follows:

Temporal realization of spatial values:

Three-dimensional model of the Roessler attractor:

Wham! Slightly changed values:
Attractor with slightly modified initial conditions (trajectories are different!)
Attractor for other coefficients in the system of equations (the chaotic process turned into a periodic one!)


Attractor for other coefficients in the system of equations (the chaotic process turned into a periodic one!)

Compare pictures of three-dimensional attractors under different initial conditions and coefficients in the system of equations. See how dramatically the trajectories of movement in the first case? But one way or another they are concentrated near a single region of attraction. In the second case, the attractor in general ceased to show signs of chaos, turning into a closed periodic loop (limit cycle).
Attractor Rikitake
Dynamo Rikitake is one of the known third-order dynamical systems with chaotic behavior. It is a model of a two-disk dynamo and was first proposed in problems of the chaotic inversion of the geomagnetic field of the Earth. The scientist Rikitake investigated a dynamo system with two interconnected disks constructed in such a way that the current from one disk coil flowed into another and excited the second disk, and vice versa. At some point, the system began to crash and show unpredictable things. Active studies of the attractor allowed the Rikitake dynamo to be projected onto the coupling model of large magnetic field vortices in the core of the Earth.
Dynamo Rikitake is described by the following system of equations:

Model Dynamo Rikitake in MATLAB:

Temporary implementation:

Attractor (first version):

Dynamo (second version)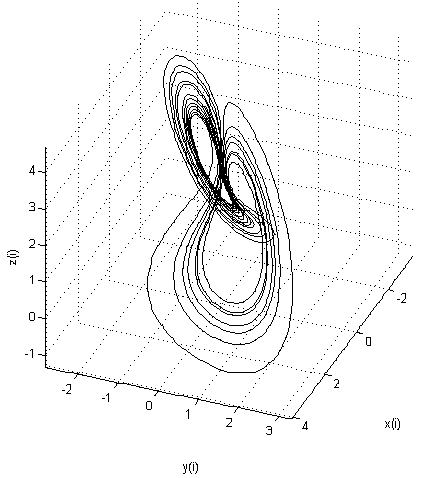

You may notice that the Rikitake dynamo is somewhat similar to the Lorenz attractor, but these are completely different systems and describe different physical processes!
Nose-Hoover Attractor
A less famous, but no less important, three-dimensional dynamic system is the Nose-Hoover thermostat . Used in molecular theory as a reversible in time thermostatic system. Unfortunately, I don’t know so much about this attractor as about the others, but I found it interesting and I included it in the review.
The Nose-Hoover thermostat is described by the following system of equations:
Nose Hoover model in MATLAB:

Temporary implementation:

Two-dimensional projections of the attractor:

Three-dimensional model of the Nose-Hoover thermostat:

Thermostat (second version)

Project Synthesis
To synthesize the project, you need to click on the red “X” icon, which will launch the System Generator settings. Here you can select the FPGA family and type, the resulting file format (VHDL / Verilog - for creating source codes, NGC - for creating a kernel in the form of a list of connections), preliminary clock frequencies, etc. My typical settings are shown in the following figure:

After installing all the settings - click "Generate" and at the output we have a synthesized project for the FPGA. Then it’s easy to insert the generated kernel into the part of the project you need. (How this is done, you can find in my other articles on digital signal processing). All listed attractors occupy very few resources in modern FPGA crystals (about 10-20 DSP48 blocks and a bit of logic).
Life examples
Lorenz attractor on the oscilloscope screen:

A system of galaxies similar to the Lorenz attractor:


A system of galaxies similar to the Lorenz attractor:

Conclusion
These attractors are used in many physical processes in various fields of science and technology - from physics and chemistry to mechanics and meteorology. In particular, chaos generators are used to create long sequences of pseudo-random numbers (PRS). In the tasks of radio engineering, chaos can be used to modulate a carrier when creating ultra-wideband signals by digital methods (on FPGAs or processors).
Chaos theory is an interesting and amazing science. And thanks to modern analysis and modeling tools, it becomes quite attractive for research. With the help of this article you can independently model your own dynamical systems, up to hyperchaotic systems of order higher than 3 (for example, Lorentz hyperhaos, Rossler, etc.). I hope, the material of my publication can be useful to someone, and someone will find something new and useful for themselves.
Attractor source files on Github
My articles on similar topics:
Literature
- Chaos on Habré!
- Chaoscope Online
- Chaos. Creating a new science
- Chaos Theory - Wiki
- Lorenz Attractor - Wiki
- Rössler Attractor - Wiki
- Elegant chaos (also sold in Russian)
Hooray, the Hub FPGA is back for Habr. Happy New Year, everyone!
Source: https://habr.com/ru/post/273915/
All Articles