On the complexity of growing sakura: how I participated in Ludum Dare 34
Hi, Habr!
This post will discuss my participation in the Ludum Dare 34 competition, which was about three weeks ago.
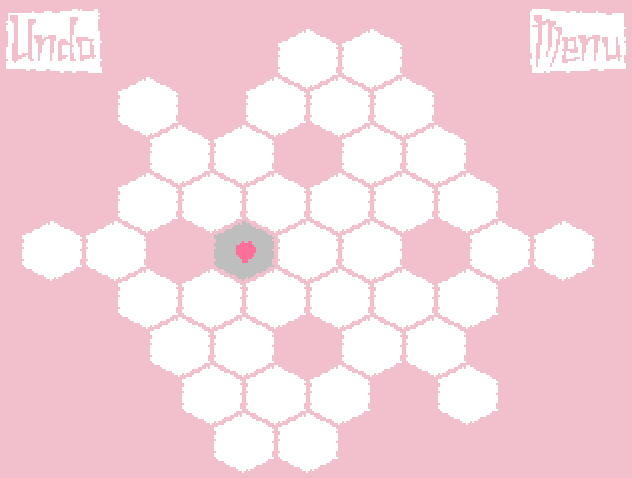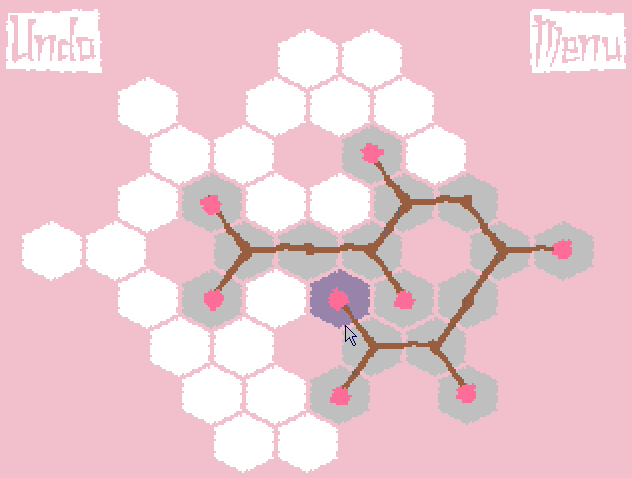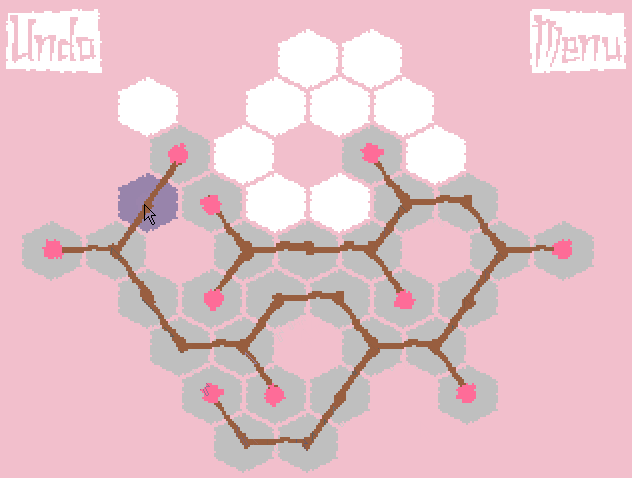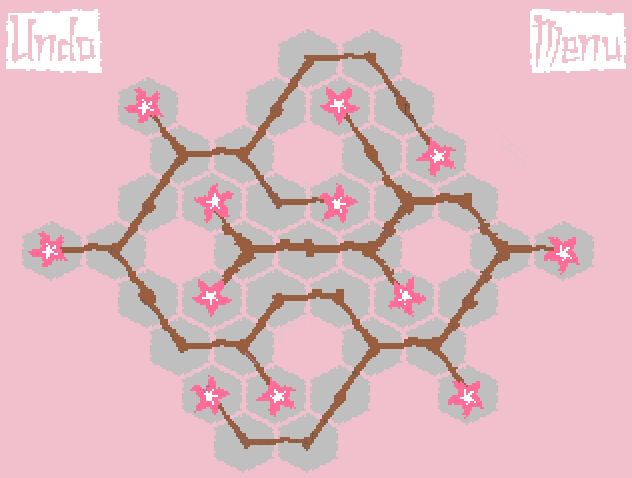
The result was a puzzle called Growing Sakura, the gameplay of which can be seen on the gif (do not worry, it weighs only 300Kb):
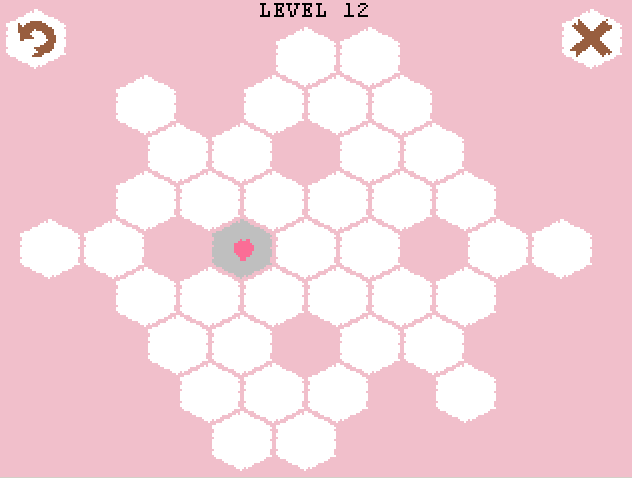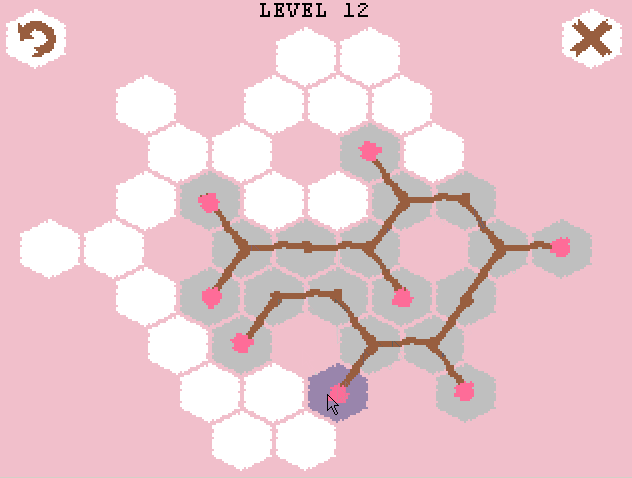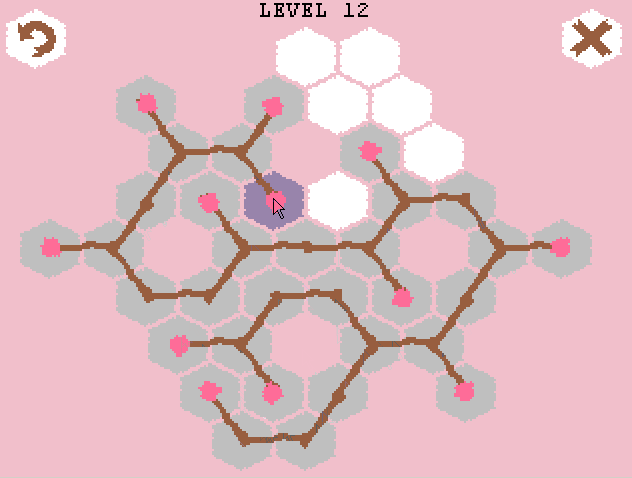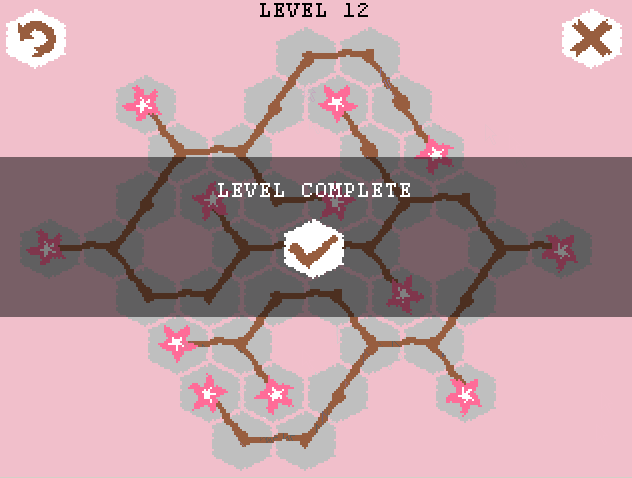
')
Briefly about the rules of the game: initially we have a hexagonal field and several root buds (or one, as in the gif above). From it you can make 3 branches (in two ways - by clicking the left or right mouse button). From each bud on a branch, you can make a Y-fork for the left click of the mouse, and just continue the branch further (I-fork) for the right one. If a branch cannot grow in any direction (the corresponding cell is busy or there is no cell in the desired direction), then the branch does not grow. In accordance with the last condition, it is necessary to choose the order of "unfolding" the branches. The result will be a tree (or several trees) such that there are no sharp corners between two adjacent branches. The goal of the game is to cover all the cells of the playing field.
Without looking under the cut try to think about 10 seconds and estimate how difficult this game can be.
This competition is held once every 4 months and this time it was already the 34th event in a row. The essence of the competition (in the Compo nomination): it takes 48 hours to create a computer game on a given topic. The theme becomes known in the first minutes of the competition. The game should be created solo and from scratch (everything from scratch: code, graphics, sounds, etc.), however, third-party programs and code developments are allowed, but they must be announced in advance (say, in my blog on Ludum Dare website). I will use Paint, Unity, C ++ and Delphi, here’s a link to the start project template ”). There is also a simplified relaxing nomination Jam, where you can play a game with the team for as much as 72 hours, use old practices and even (oh, horror!) You do not need to publish the source code at the end with the game. However, for me personally, the nomination Jam is not interesting, I sometimes go into it only if I do not have time to meet the 48 hours.
The topic of the competition is determined by voting, and this time the largest number of votes were cast at once by two topics: “Growing” and “Two Button Controls”. You could use either of these topics, or both. Interpretation of the topic is left to the discretion of the participant: for example, the first topic could be interpreted as “Growth”, “Growing Up” or “Growing Up”, and the second one - “Control of two buttons” or “Power of two buttons”. As can be seen from the description of the game above, I have in a sense connected the two topics together.
When I woke up, the contest was already going on for a couple of hours. The topic of obvious solutions is not offered. Slowly having breakfast and pouring coffee, I thought about something that would fit the interesting under this topic. Of course, I wanted to combine both topics together. Several concepts have surfaced:
All these concepts were either boring or too difficult to implement (and before this contest I had a month of hard labor for work and study, so I didn’t want to strain myself). There was also an idea to make a clone of Super Hexagon (there are two buttons on it!), But I scored on this idea, because there was no “Growing”. By the middle of the day, the following concept emerged, which was obtained by simplifying the idea of the settlers:
The rules of the game arose from the following mathematical problem:
So, I just assumed that by following such rules you can make some rather complicated puzzle.
Quickly sketched a prototype of game mechanics:
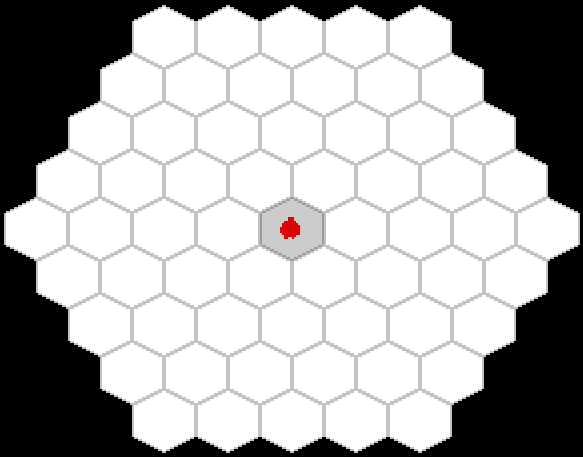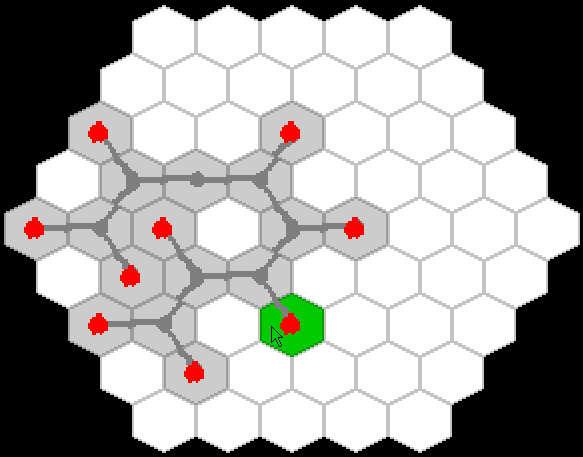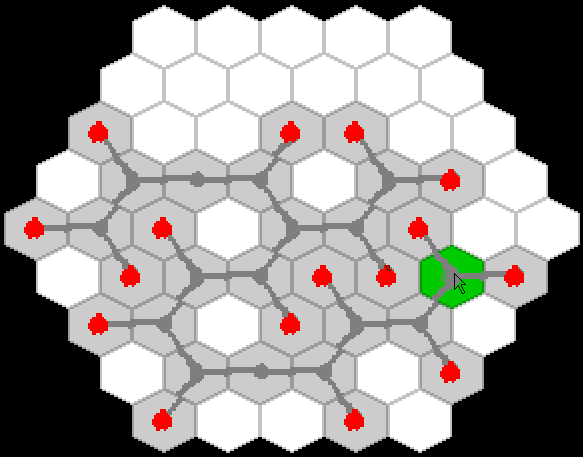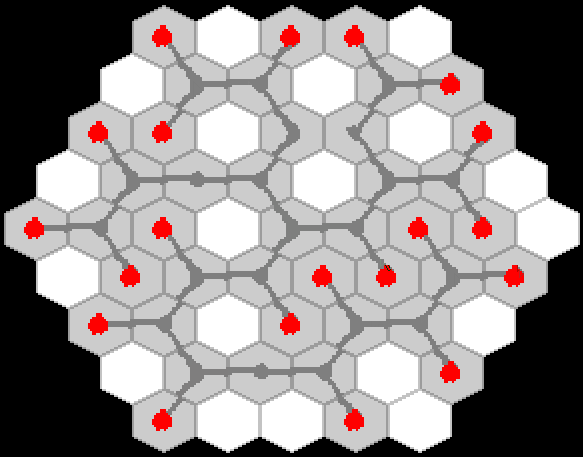
And he saw that it was good!
At the end of the first day, the idea of growing roots was transformed into the idea of growing branches of sakura (but in the game code all objects are still named according to the roots!). To simplify the game, all the numbers were thrown out and the goal was reduced to the simplest form: simply cover the entire playing field. The prototype of the game has grown to the following:
There was an idea to make the branches of the tree become thicker in accordance with the distance to the farthest leaf (and this can be seen on the gif). However, for long branches, the stretching became so large that their appearance deteriorated. I spent quite a lot of time on making everything beautiful. In the end, he scored - many more things had to be done. From now on, all branches remained the same thickness.
At this point I decided to finish the first day and went to bed.
As usual, in the dream after the first day I decided not to save, and instead not to sleep the second night. In the morning I was sitting inventing levels. He even sketched a hexagonal grid in the Word and unpacked it, waving further with a pencil and an eraser. It became clear that without an automatic solver it would be difficult to continue.
No sooner said than done. Sketched a simple puzzle solver in C ++. He recursively sorts through all the possible actions of the player and looks at whether the puzzle is solved or not. At each iteration of iteration, the current state of the game is stored in std :: set. If later there is the same state of the game - then the search is rolled back. Thus, the solver does not consider the same scenarios of events a hundred times.
It turned out that the puzzle mentioned above on two gifs (let's call it puzzle A) has already 47 different solutions. It took 93 seconds to complete a search, at that 10810446 game states were examined. This solver helped greatly in the future.
An example of the work of a solver for another level:
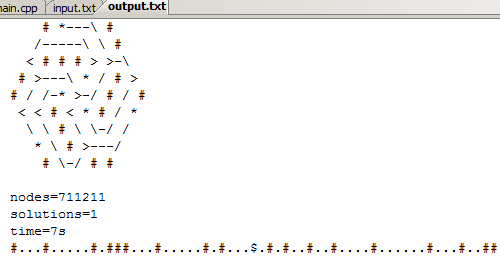
This level was resolved in 7 seconds, 711211 states were saved in std :: set and exactly one solution was found. The strange line at the very bottom is the level description, which is inserted into the game itself.
A little later, the solver was optimized by the “single cell” heuristic. Namely: if at some step one of the free cells was surrounded by occupied cells ("walls" or cells into which the sakura branches had already sprouted), and it was impossible to put a branch into this cell from neighboring ones - then it became clear that there were no solutions and bust rolled back. After adding this heuristic, puzzle A began to be processed in 5 seconds with the number of considered states only 723225.
Until the end of the second day, I used to draw interesting game grids and solve them with my program. In the meantime, I added a menu to the game (well, what else to do when the solver enumerates the solutions?), Redraw the icons. The game began to look like this:

As you can see from the gif, I set myself a rather ambitious task: to develop as many as 40 puzzles. By the time of the creation of the gifs, only 17 levels out of 40 were ready. By the end of the competition, the night remained, namely, about 10 hours.
Some of the levels were generated as follows: some symmetrical figure was drawn, a root bud poked into its random cell. After that, the solver was launched. If the resulting solutions produced too much or none at all, the level was slightly modified (slightly change the shape or transplant the root sprout somewhere else) and the solver started again, and so on until the appropriate level was built.
For other levels, the figure was intentionally asymmetric, usually there several branches of sakura converged into a common “com”, after which it was necessary to weave them carefully with each other. These levels were also created using a solver.
Next, I began to add levels that had several root buds. The game immediately became much more diverse! An example of a level with several buds:

Yes, sometimes for the passage of the level can not cover just one cell ...
At night, I added a game screen to the game with the rules of the game, created a few sounds with the help of the wonderful program Bosca Ceoil and finally finished off all 40 levels (forty, Karl!) As planned. The last levels are so complex that they are not completely amenable to my solver: he finds several solutions before him, how his memory ends, and he crashes. Therefore, I do not know exactly how many solutions are there, although it can be said with confidence that all the puzzles in the game have a solution.
The game was over at the last hour and with weak hands was withdrawn on the competition website.

After the end of the competition, the organizers allocate 3 weeks to the vote. Ludum Dare members download games from other members and rate them. I also did this for about a week, and at the same time everyone thought how much the Growing Sakura game can be difficult. As a result, everything resulted in the following:
Here I will try to present my evidence (I hope I did not screw it up anywhere in it!).
In this article, you can find evidence that the problem of checking the existence of a Hamiltonian cycle in a planar cubic 3-connected graph is NP-complete (let's call its problem X for brevity). Immediately decipher all incomprehensible words:
A graph is a few points (they are called vertices), some pairs of which are connected by lines (they are called edges). A graph is called planar if it can be positioned on a plane so that the edges do not intersect. A graph is called cubic if exactly 3 edges emanate from each of its vertices. A graph is called 3-connected , if in order to annoy it at least into 2 parts, at least 3 edges must be removed. A Hamiltonian cycle in a graph is a sequence of pairwise distinct vertices v 1 , v 2 , ..., v n such that v i and v i + 1 are connected by an edge for any 1 <= i <n, and also by an edge are connected the vertices of v n and v 1 , where n is the number of vertices in the graph. For example, the following picture shows a Hamiltonian cycle in a planar cubic 3-connected graph:

The definition of NP-difficulty and NP-completeness is not so simple. But I will try to briefly clarify the case under the spoiler.
For formality, we formulate Problem X and the Growing Sakura game as a solvability problem.
Problem X: “Given a cubic planar 3-connected graph G, is it true that there exists a Hamiltonian cycle in it?”.
Growing Sakura game: “The level from the Growing Sakura game is given, is it true that he has a solution?”.
Well, we will reduce the NP-complete task X to the game Growing Sakura. Those. according to the input data of problem X, we construct such a level for Growing Sakura that its solution will also give an answer for the initial problem X. In this way we will show that task X is no more difficult than the game Growing Sakura.
For this we need the following constructions:
Everything is simple here - a branch of sakura that comes from any of the three sides can grow further in both directions simultaneously.


For a given element, a sakura branch should choose exactly one direction out of two (in fact, no more than one, but this action is meaningless). The second direction will have to be covered later and on the other side.
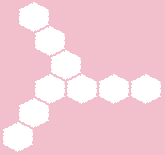

This design is a kind of diode. She skips the sakura branch in one direction only.

Those. in this direction skips:

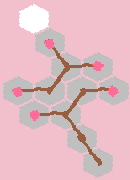
But this is not:

I was not able to come up with the same construction without additional root points, maybe you can?
The most complex element, its construction took quite a lot of time.

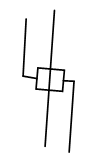
The essence of this element is as follows. It has solutions only in the following configurations:
but)
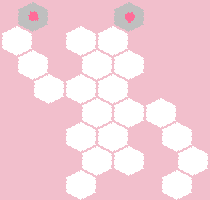

b)
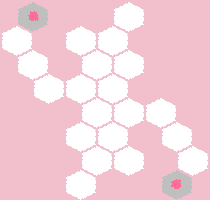

However, there are no solutions in the following configuration:

Moreover, it is impossible even to cover any of the crosses without obtaining the situation of a “single cell”.
From the OR-gadgets it is already possible to collect the first approximation to a planar cubic 3-connected graph. But, the rules of the game require that the ribs, which are not included in the Hamiltonian cycle, also be covered. And to ensure this, we need a more cumbersome design. Here she is:
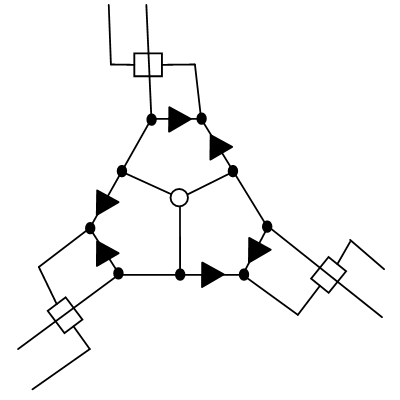
This construction corresponds to one vertex in our cubic graph.
Let's now look at how it works. Without loss of generality, let the sakura branch come from the bottom left (in two ways at once). Then the next part of the scheme will be covered:

Now, depending on which of the two options we choose, we get the following developments:
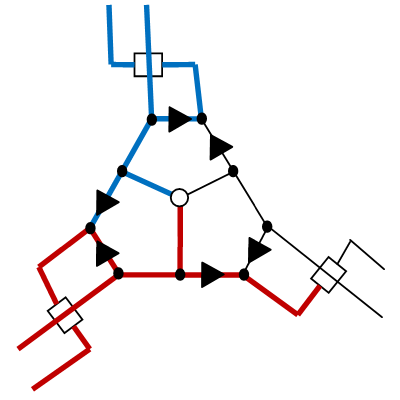

Note that in both cases we sent two sakura branches in one of the directions and exactly one of them in the other direction. Those. we painted one edge in the graph in one direction, but not in the other. Now, when our Hamiltonian path reaches the top of the graph where we haven’t painted the edge now, another branch will come from there (marked below in green), which unlocks the LOCK gadget and covers everything that needs to be covered:
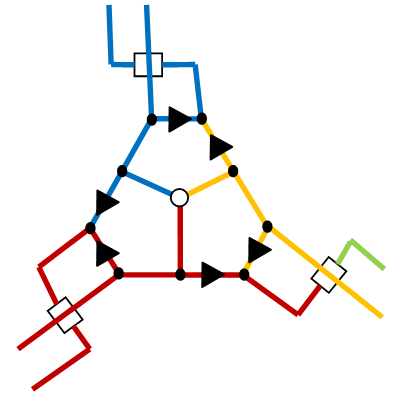

Cases when we came to the summit, for which one or two adjacent peaks have already been visited by our way, are invited to analyze the reader independently.
Well, now just for the entire planar cubic 3-connected graph, we will build a huge level, check if it has a solution.If there is - then it is easy to restore the cycle for the original graph - just look at how the branch of sakura grows in OR-gadgets (although, formally, it is not required to restore it explicitly). It is always possible to build such a level - all gadgets can be rotated and connected by a chain of cells of sufficient length. Since initially the graph is planar, there is no need to solve the problem of crossing paths.
It would seem that all proved? No, not proven. At the constructed level, there will be no solution at all - we have not initiated the process of "chain reaction" - the Hamiltonian path has no place to start. This is solved very simply. We take any edge (or rather, the corresponding LOCK gadget) and do this: The
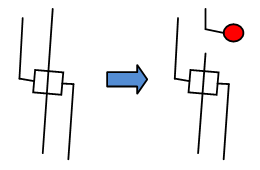
red circle is where we begin to grow our branch. And we definitely need to cover the terminating end so that the Hamiltonian cycle closes!
Now proved? No! Suddenly, in the graph there is a Hamiltonian cycle that does not pass along the edge from which we began to look for it! What to do?It is necessary to try to search for a cycle starting from another edge. Obviously, for any two edges emerging from one vertex, at least one of them will pass the desired Hamiltonian path, if it exists. Therefore, to solve problem X, no more than two levels of Growing Sakura will be needed.
“Allow me!” - you will say, “it was written a little higher that we will solve only one level of the Growing Sakura game, equivalent to the column in Problem X!” That's right, I deceived you brazenly! However, the proof of this does not spoil - I just used the Kuk data , and not Karp data .
Now the NP-difficulty of Growing Sakura is proven! Cheers, comrades!

As is known, an NP-complete problem, if it is NP-hard and lies in the class NP. The first point we proved a little higher.
The affiliation of this problem to the NP is quite obvious. Recall that a task belongs to the NP class, if the solution to this problem is one of the “yes” or “no” answers, and there is a certificate for the “yes” answer, which allows you to verify that the answer is indeed “yes” in polynomial time. Well, indeed, for the Growing Sakura game, the certificate can be written as a string of length O (n), saving in what order and button we clicked on the corresponding cells, where n is the number of cells in the field. Well, for O (n), you can verify that the certificate is “valid” by simply expanding branches according to the certificate and the rules of the game.
Cheers, Growing Sakura NP is full! If suddenly someone writes a solver for this game that works in polynomial time, you can pick up your million .
The fact that Growing Sakura is NP-complete does not mean that all levels in this game will be prohibitively difficult. It simply means that such levels can be created. And the rest is already dependent on the design levels. Many of the classic Nintendo games are known to be NP-hard, and that doesn’t stop them from enjoying them. Even such a kazualka like Candy Crush is NP-hard , not to mention Tetris , sapper and other sudoku .
Voting on Ludum Dare will end tomorrow, in the update I will publish what place I managed to get. I hope to enter the hundred best games.
Links: game page on Ludum Dare , Dropbox , Itch.io .
UPD. , . Compo 1232 . Growing Sakura 10 ( ). : #4 Theme, #5 Innovation, #22 Fun.
This post will discuss my participation in the Ludum Dare 34 competition, which was about three weeks ago.
The result was a puzzle called Growing Sakura, the gameplay of which can be seen on the gif (do not worry, it weighs only 300Kb):

')
Briefly about the rules of the game: initially we have a hexagonal field and several root buds (or one, as in the gif above). From it you can make 3 branches (in two ways - by clicking the left or right mouse button). From each bud on a branch, you can make a Y-fork for the left click of the mouse, and just continue the branch further (I-fork) for the right one. If a branch cannot grow in any direction (the corresponding cell is busy or there is no cell in the desired direction), then the branch does not grow. In accordance with the last condition, it is necessary to choose the order of "unfolding" the branches. The result will be a tree (or several trees) such that there are no sharp corners between two adjacent branches. The goal of the game is to cover all the cells of the playing field.
Without looking under the cut try to think about 10 seconds and estimate how difficult this game can be.
What is Ludum Dare?
This competition is held once every 4 months and this time it was already the 34th event in a row. The essence of the competition (in the Compo nomination): it takes 48 hours to create a computer game on a given topic. The theme becomes known in the first minutes of the competition. The game should be created solo and from scratch (everything from scratch: code, graphics, sounds, etc.), however, third-party programs and code developments are allowed, but they must be announced in advance (say, in my blog on Ludum Dare website). I will use Paint, Unity, C ++ and Delphi, here’s a link to the start project template ”). There is also a simplified relaxing nomination Jam, where you can play a game with the team for as much as 72 hours, use old practices and even (oh, horror!) You do not need to publish the source code at the end with the game. However, for me personally, the nomination Jam is not interesting, I sometimes go into it only if I do not have time to meet the 48 hours.
The topic of the competition is determined by voting, and this time the largest number of votes were cast at once by two topics: “Growing” and “Two Button Controls”. You could use either of these topics, or both. Interpretation of the topic is left to the discretion of the participant: for example, the first topic could be interpreted as “Growth”, “Growing Up” or “Growing Up”, and the second one - “Control of two buttons” or “Power of two buttons”. As can be seen from the description of the game above, I have in a sense connected the two topics together.
The first day
When I woke up, the contest was already going on for a couple of hours. The topic of obvious solutions is not offered. Slowly having breakfast and pouring coffee, I thought about something that would fit the interesting under this topic. Of course, I wanted to combine both topics together. Several concepts have surfaced:
- A puzzle that emulates a window manager: there are a lot of windows on the screen (with two buttons each!), They all need to be closed, but everything is complicated by the fact that both available buttons sometimes perform very tricky actions (say, close the window to the right of this). As a joke, there was an idea to make windows with the title “Agreement” filled with text like “Bla-bla-bla-bla” with two buttons “Agree” and “Disagree”, which simply close this window.
- Strategy-bagel: the development of an underground base. The base consists of square tiles, with each of which you can do one of two actions, thus expanding (growing!) The base.
- Some strange mechanism, consisting of a heap of units, on each unit there are two buttons "On" and "Off".
- Again a strategy, this time a minimalistic clone of Settlers II. Hexagonal tiles, again, you can do one of two actions (more roads or build a house). The idea was that in order to build steeper buildings, several roads had to be led to the tile. But experiments on a piece of paper showed that the roads somehow ended quickly, which stopped the growth of the settlement.
All these concepts were either boring or too difficult to implement (and before this contest I had a month of hard labor for work and study, so I didn’t want to strain myself). There was also an idea to make a clone of Super Hexagon (there are two buttons on it!), But I scored on this idea, because there was no “Growing”. By the middle of the day, the following concept emerged, which was obtained by simplifying the idea of the settlers:
- There is a hexagonal field, in some cells - stones, in some - beans. And we have to grow the roots of some plants from beans. The roots are grown according to the rules that were described at the very beginning of this post. For each bean, it is known how many cells the root system has to cover in order for the bean tree to grow large and healthy. Well, the player's task is to grow the roots so that all the beans grow.
The rules of the game arose from the following mathematical problem:
Math problem
The plane is tiled with equal regular triangles (or, in other words, a triangular parquet is given). The points where the vertices of the triangles meet are called nodes, 6 edges emanate from each node. Some edges are colored red, and between any two adjacent red edges on the top is either 120 degrees or 180 (there are no sharp corners). Prove that there are two nodes such that one of them cannot get into the other, moving along the red edges.
So, I just assumed that by following such rules you can make some rather complicated puzzle.
Quickly sketched a prototype of game mechanics:

And he saw that it was good!
At the end of the first day, the idea of growing roots was transformed into the idea of growing branches of sakura (but in the game code all objects are still named according to the roots!). To simplify the game, all the numbers were thrown out and the goal was reduced to the simplest form: simply cover the entire playing field. The prototype of the game has grown to the following:

There was an idea to make the branches of the tree become thicker in accordance with the distance to the farthest leaf (and this can be seen on the gif). However, for long branches, the stretching became so large that their appearance deteriorated. I spent quite a lot of time on making everything beautiful. In the end, he scored - many more things had to be done. From now on, all branches remained the same thickness.
At this point I decided to finish the first day and went to bed.
Second day
As usual, in the dream after the first day I decided not to save, and instead not to sleep the second night. In the morning I was sitting inventing levels. He even sketched a hexagonal grid in the Word and unpacked it, waving further with a pencil and an eraser. It became clear that without an automatic solver it would be difficult to continue.
No sooner said than done. Sketched a simple puzzle solver in C ++. He recursively sorts through all the possible actions of the player and looks at whether the puzzle is solved or not. At each iteration of iteration, the current state of the game is stored in std :: set. If later there is the same state of the game - then the search is rolled back. Thus, the solver does not consider the same scenarios of events a hundred times.
It turned out that the puzzle mentioned above on two gifs (let's call it puzzle A) has already 47 different solutions. It took 93 seconds to complete a search, at that 10810446 game states were examined. This solver helped greatly in the future.
An example of the work of a solver for another level:

This level was resolved in 7 seconds, 711211 states were saved in std :: set and exactly one solution was found. The strange line at the very bottom is the level description, which is inserted into the game itself.
A little later, the solver was optimized by the “single cell” heuristic. Namely: if at some step one of the free cells was surrounded by occupied cells ("walls" or cells into which the sakura branches had already sprouted), and it was impossible to put a branch into this cell from neighboring ones - then it became clear that there were no solutions and bust rolled back. After adding this heuristic, puzzle A began to be processed in 5 seconds with the number of considered states only 723225.
Until the end of the second day, I used to draw interesting game grids and solve them with my program. In the meantime, I added a menu to the game (well, what else to do when the solver enumerates the solutions?), Redraw the icons. The game began to look like this:

As you can see from the gif, I set myself a rather ambitious task: to develop as many as 40 puzzles. By the time of the creation of the gifs, only 17 levels out of 40 were ready. By the end of the competition, the night remained, namely, about 10 hours.
Some of the levels were generated as follows: some symmetrical figure was drawn, a root bud poked into its random cell. After that, the solver was launched. If the resulting solutions produced too much or none at all, the level was slightly modified (slightly change the shape or transplant the root sprout somewhere else) and the solver started again, and so on until the appropriate level was built.
For other levels, the figure was intentionally asymmetric, usually there several branches of sakura converged into a common “com”, after which it was necessary to weave them carefully with each other. These levels were also created using a solver.
Next, I began to add levels that had several root buds. The game immediately became much more diverse! An example of a level with several buds:

Yes, sometimes for the passage of the level can not cover just one cell ...
At night, I added a game screen to the game with the rules of the game, created a few sounds with the help of the wonderful program Bosca Ceoil and finally finished off all 40 levels (forty, Karl!) As planned. The last levels are so complex that they are not completely amenable to my solver: he finds several solutions before him, how his memory ends, and he crashes. Therefore, I do not know exactly how many solutions are there, although it can be said with confidence that all the puzzles in the game have a solution.
The game was over at the last hour and with weak hands was withdrawn on the competition website.

After the end of the competition, the organizers allocate 3 weeks to the vote. Ludum Dare members download games from other members and rate them. I also did this for about a week, and at the same time everyone thought how much the Growing Sakura game can be difficult. As a result, everything resulted in the following:
Growing Sakura is NP-hard
Here I will try to present my evidence (I hope I did not screw it up anywhere in it!).
In this article, you can find evidence that the problem of checking the existence of a Hamiltonian cycle in a planar cubic 3-connected graph is NP-complete (let's call its problem X for brevity). Immediately decipher all incomprehensible words:
A graph is a few points (they are called vertices), some pairs of which are connected by lines (they are called edges). A graph is called planar if it can be positioned on a plane so that the edges do not intersect. A graph is called cubic if exactly 3 edges emanate from each of its vertices. A graph is called 3-connected , if in order to annoy it at least into 2 parts, at least 3 edges must be removed. A Hamiltonian cycle in a graph is a sequence of pairwise distinct vertices v 1 , v 2 , ..., v n such that v i and v i + 1 are connected by an edge for any 1 <= i <n, and also by an edge are connected the vertices of v n and v 1 , where n is the number of vertices in the graph. For example, the following picture shows a Hamiltonian cycle in a planar cubic 3-connected graph:

The definition of NP-difficulty and NP-completeness is not so simple. But I will try to briefly clarify the case under the spoiler.
Argument about all NP
The problem of solvability ( decision problem ) is a question formulated within the framework of a formal system, to which you can answer "yes" or "no." For example, the question “Given x and y, is it true that x is divisible by y?” Is a solvability problem. But the question “How much is A + B?” Is not a solvability problem.
The NP class is a set of such solvability problems for which the “yes” answer can be checked in polynomial time with some additional information (the so-called certificate ). Moreover, for any input parameters, if the answer is "yes", the certificate must necessarily exist (and not so that for some input data when the answer is "yes" it is, and for some it is not). For example, for the solvability problem “There is a graph G for n vertices, is it true that there is a Hamiltonian cycle in it?” The certificate is (for example!) The Hamiltonian cycle itself is a sequence of n numbers indicating in what order this Hamiltonian graph is bypassed. So it lies in the class NP.
Very similar to the NP class, the so-called co-NP class — a set of such solvability problems, for which the answer “no” can be checked in polynomial time if there is additional information (the so-called counter - example ). For example, for the solvability problem “Here is the number X, is it true that it is simple?” The counterexample is a divisor of the number X, different from 1 and X. So this problem lies in the class co-NP. Again, for each “no”, a counterexample is necessarily needed.
There is also a class P - the set of all solvability problems that can be solved in polynomial time. Note that formally in P exactly the solvability problems lie, i.e. the question "How many will be A + B?" is not included! (He enters a slightly different FP class ). But problems of this kind can always be reformulated into a series of solvability problems by adding another parameter k: “Is it true that the k-th bit of the A + B expression is 1?”. Having made a series of such queries, we, in fact, polynomially reduce, according to Cook, the question “How many are A + B?” To the solvability problem. But more about that below.
Any task from class P lies in class NP, since the answer “yes” can be checked in polynomial time using any certificate in general (for example, the certificate “ I swear by my mother! ”). The verification algorithm is as follows: throw out the certificate and just find the answer to the original question from scratch in polynomial time. For the same reason, any problem from the class P also lies in the class co-NP.
Once again about the intricacies of belonging to classes. The question “Is it true that the number X is simple?” Belongs to co-NP, and the question “Is it true that the number X is composite?” Belongs to NP. According to the three Hindus algorithm , both of these questions can be answered in polynomial time. So both of these questions, among other things, belong to the class P! However, these two questions have little in common with the following very similar question: “What is the smallest divisor of X, greater than 1?” (Which is not included in either NP or co-NP, and no one can answer for polynomial time for it (and RSA encryption is good!)). Those. Look, the question “Is it true that X is composite?” lies in NP, because for the answer “yes” there is a certificate - a divisor X between 1 and X, which allows you to check in polynomial time that the answer is really “yes”. But, thanks to the algorithm of the three Indians, the " Mom swear! " Is also a suitable certificate, i.e. the algorithm that solves the problem should not provide the certificate that indicates that the task belongs to the class NP!
By the way, there are solvability problems that do not belong to either P or NP or co-NP. For example, the classic problem of stopping : “The program code is given, is it true that it will be executed in a finite time?”. But that's another story ...
Now for polynomial reducibility. There are several schemes for reducing problems to each other.
According to Karp , problem U is considered polynomially reducible to problem V, if for any input data u for task U we can convert them into polynomial time into input data v for task V, feed them to V, and get an answer (which is "yes" or " no ", remember?), which will be the answer to the original task of U.
According to Cook , problem U is considered polynomially reducible to problem V if there exists an algorithm polynomial in time that solves problem U, while using problem V as an oracle , i.e. the algorithm can build as many (but a polynomial number!) sets of input data for task V and find out the answer for one iteration.
Both of these data show that, in a sense, task U is no more complicated than task V. That is, if we are able to solve V in a certain sense quickly, then we can also solve U in a certain sense quickly. And if we are not able to solve U in a certain sense quickly, then we cannot solve quickly in a certain sense either. Thus, the above-mentioned question “How much is A + B?” Is not more difficult than the question “Is it true that the k-th bit of A + B expression is 1?”, And since the second one is in P, the first question is easy to answer ( in polynomial time!), although it does not lie in P.
In essence, Karp information is a special case of Cook information, i.e. in the case of information on Karp, the oracle is called only once at the very end and his answer without any changes is considered to be the answer to the original problem. Well and also, in the case of information on Cook, problems U and V do not necessarily have to be problems of solvability.
A problem from the NP class is called NP-complete if any problem from the NP class (that is, any!) Polynomially reduces to it. The task of satisfiability of Boolean formulas (SAT) is the first problem for which NP-completeness was proved by explicitly reducing any problem from the class NP to the SAT. Those. SAT is a kind of universal task, which, being an oracle , allows you to quickly solve any problem from the class NP. Later it was discovered that a huge number of other tasks from the NP class are also NP-complete! Usually, this is easily proved by polynomial mixing of some other NP-complete problem (as a rule, SAT, possibly through a chain of other tasks) to this one.
A task is called NP-hard if any NP-complete problem reduces to it. If this NP-hard problem also belongs to the class NP itself, then it is obviously an NP-complete problem. An example of an NP-hard task that does not belong to the NP class is the problem of packing into containers “What is the smallest number of containers you can pack all these items?”, Because the NP-complete problem of sharing “Can you divide all these items into two equal by the total weight of the heap?
The biggest question in all this demagogy is this: is any NP-complete problem solved in polynomial time? If so, then P = NP and any task from the NP class can be solved in polynomial time and this is very good for many applied combinatorial problems and very bad for some encryption algorithms.
She: answer me, honestly, yes or no, ok?
He: ask
She: Why do men laugh at blondes?
He: yes
( bash about decision problem )
The NP class is a set of such solvability problems for which the “yes” answer can be checked in polynomial time with some additional information (the so-called certificate ). Moreover, for any input parameters, if the answer is "yes", the certificate must necessarily exist (and not so that for some input data when the answer is "yes" it is, and for some it is not). For example, for the solvability problem “There is a graph G for n vertices, is it true that there is a Hamiltonian cycle in it?” The certificate is (for example!) The Hamiltonian cycle itself is a sequence of n numbers indicating in what order this Hamiltonian graph is bypassed. So it lies in the class NP.
Very similar to the NP class, the so-called co-NP class — a set of such solvability problems, for which the answer “no” can be checked in polynomial time if there is additional information (the so-called counter - example ). For example, for the solvability problem “Here is the number X, is it true that it is simple?” The counterexample is a divisor of the number X, different from 1 and X. So this problem lies in the class co-NP. Again, for each “no”, a counterexample is necessarily needed.
There is also a class P - the set of all solvability problems that can be solved in polynomial time. Note that formally in P exactly the solvability problems lie, i.e. the question "How many will be A + B?" is not included! (He enters a slightly different FP class ). But problems of this kind can always be reformulated into a series of solvability problems by adding another parameter k: “Is it true that the k-th bit of the A + B expression is 1?”. Having made a series of such queries, we, in fact, polynomially reduce, according to Cook, the question “How many are A + B?” To the solvability problem. But more about that below.
Any task from class P lies in class NP, since the answer “yes” can be checked in polynomial time using any certificate in general (for example, the certificate “ I swear by my mother! ”). The verification algorithm is as follows: throw out the certificate and just find the answer to the original question from scratch in polynomial time. For the same reason, any problem from the class P also lies in the class co-NP.
Once again about the intricacies of belonging to classes. The question “Is it true that the number X is simple?” Belongs to co-NP, and the question “Is it true that the number X is composite?” Belongs to NP. According to the three Hindus algorithm , both of these questions can be answered in polynomial time. So both of these questions, among other things, belong to the class P! However, these two questions have little in common with the following very similar question: “What is the smallest divisor of X, greater than 1?” (Which is not included in either NP or co-NP, and no one can answer for polynomial time for it (and RSA encryption is good!)). Those. Look, the question “Is it true that X is composite?” lies in NP, because for the answer “yes” there is a certificate - a divisor X between 1 and X, which allows you to check in polynomial time that the answer is really “yes”. But, thanks to the algorithm of the three Indians, the " Mom swear! " Is also a suitable certificate, i.e. the algorithm that solves the problem should not provide the certificate that indicates that the task belongs to the class NP!
By the way, there are solvability problems that do not belong to either P or NP or co-NP. For example, the classic problem of stopping : “The program code is given, is it true that it will be executed in a finite time?”. But that's another story ...
Now for polynomial reducibility. There are several schemes for reducing problems to each other.
According to Karp , problem U is considered polynomially reducible to problem V, if for any input data u for task U we can convert them into polynomial time into input data v for task V, feed them to V, and get an answer (which is "yes" or " no ", remember?), which will be the answer to the original task of U.
According to Cook , problem U is considered polynomially reducible to problem V if there exists an algorithm polynomial in time that solves problem U, while using problem V as an oracle , i.e. the algorithm can build as many (but a polynomial number!) sets of input data for task V and find out the answer for one iteration.
Both of these data show that, in a sense, task U is no more complicated than task V. That is, if we are able to solve V in a certain sense quickly, then we can also solve U in a certain sense quickly. And if we are not able to solve U in a certain sense quickly, then we cannot solve quickly in a certain sense either. Thus, the above-mentioned question “How much is A + B?” Is not more difficult than the question “Is it true that the k-th bit of A + B expression is 1?”, And since the second one is in P, the first question is easy to answer ( in polynomial time!), although it does not lie in P.
In essence, Karp information is a special case of Cook information, i.e. in the case of information on Karp, the oracle is called only once at the very end and his answer without any changes is considered to be the answer to the original problem. Well and also, in the case of information on Cook, problems U and V do not necessarily have to be problems of solvability.
A problem from the NP class is called NP-complete if any problem from the NP class (that is, any!) Polynomially reduces to it. The task of satisfiability of Boolean formulas (SAT) is the first problem for which NP-completeness was proved by explicitly reducing any problem from the class NP to the SAT. Those. SAT is a kind of universal task, which, being an oracle , allows you to quickly solve any problem from the class NP. Later it was discovered that a huge number of other tasks from the NP class are also NP-complete! Usually, this is easily proved by polynomial mixing of some other NP-complete problem (as a rule, SAT, possibly through a chain of other tasks) to this one.
A task is called NP-hard if any NP-complete problem reduces to it. If this NP-hard problem also belongs to the class NP itself, then it is obviously an NP-complete problem. An example of an NP-hard task that does not belong to the NP class is the problem of packing into containers “What is the smallest number of containers you can pack all these items?”, Because the NP-complete problem of sharing “Can you divide all these items into two equal by the total weight of the heap?
The biggest question in all this demagogy is this: is any NP-complete problem solved in polynomial time? If so, then P = NP and any task from the NP class can be solved in polynomial time and this is very good for many applied combinatorial problems and very bad for some encryption algorithms.
For formality, we formulate Problem X and the Growing Sakura game as a solvability problem.
Problem X: “Given a cubic planar 3-connected graph G, is it true that there exists a Hamiltonian cycle in it?”.
Growing Sakura game: “The level from the Growing Sakura game is given, is it true that he has a solution?”.
Well, we will reduce the NP-complete task X to the game Growing Sakura. Those. according to the input data of problem X, we construct such a level for Growing Sakura that its solution will also give an answer for the initial problem X. In this way we will show that task X is no more difficult than the game Growing Sakura.
For this we need the following constructions:
AND-gadget
Everything is simple here - a branch of sakura that comes from any of the three sides can grow further in both directions simultaneously.


OR-gadget
For a given element, a sakura branch should choose exactly one direction out of two (in fact, no more than one, but this action is meaningless). The second direction will have to be covered later and on the other side.


ONE-WAY-gadget
This design is a kind of diode. She skips the sakura branch in one direction only.


Those. in this direction skips:


But this is not:

I was not able to come up with the same construction without additional root points, maybe you can?
LOCK-gadget
The most complex element, its construction took quite a lot of time.


The essence of this element is as follows. It has solutions only in the following configurations:
but)


b)


However, there are no solutions in the following configuration:

Moreover, it is impossible even to cover any of the crosses without obtaining the situation of a “single cell”.
Now connect all together!
From the OR-gadgets it is already possible to collect the first approximation to a planar cubic 3-connected graph. But, the rules of the game require that the ribs, which are not included in the Hamiltonian cycle, also be covered. And to ensure this, we need a more cumbersome design. Here she is:

This construction corresponds to one vertex in our cubic graph.
Let's now look at how it works. Without loss of generality, let the sakura branch come from the bottom left (in two ways at once). Then the next part of the scheme will be covered:

Now, depending on which of the two options we choose, we get the following developments:


Note that in both cases we sent two sakura branches in one of the directions and exactly one of them in the other direction. Those. we painted one edge in the graph in one direction, but not in the other. Now, when our Hamiltonian path reaches the top of the graph where we haven’t painted the edge now, another branch will come from there (marked below in green), which unlocks the LOCK gadget and covers everything that needs to be covered:


Cases when we came to the summit, for which one or two adjacent peaks have already been visited by our way, are invited to analyze the reader independently.
Well, now just for the entire planar cubic 3-connected graph, we will build a huge level, check if it has a solution.If there is - then it is easy to restore the cycle for the original graph - just look at how the branch of sakura grows in OR-gadgets (although, formally, it is not required to restore it explicitly). It is always possible to build such a level - all gadgets can be rotated and connected by a chain of cells of sufficient length. Since initially the graph is planar, there is no need to solve the problem of crossing paths.
It would seem that all proved? No, not proven. At the constructed level, there will be no solution at all - we have not initiated the process of "chain reaction" - the Hamiltonian path has no place to start. This is solved very simply. We take any edge (or rather, the corresponding LOCK gadget) and do this: The

red circle is where we begin to grow our branch. And we definitely need to cover the terminating end so that the Hamiltonian cycle closes!
Now proved? No! Suddenly, in the graph there is a Hamiltonian cycle that does not pass along the edge from which we began to look for it! What to do?It is necessary to try to search for a cycle starting from another edge. Obviously, for any two edges emerging from one vertex, at least one of them will pass the desired Hamiltonian path, if it exists. Therefore, to solve problem X, no more than two levels of Growing Sakura will be needed.
“Allow me!” - you will say, “it was written a little higher that we will solve only one level of the Growing Sakura game, equivalent to the column in Problem X!” That's right, I deceived you brazenly! However, the proof of this does not spoil - I just used the Kuk data , and not Karp data .
Now the NP-difficulty of Growing Sakura is proven! Cheers, comrades!

Growing Sakura NP-complete
As is known, an NP-complete problem, if it is NP-hard and lies in the class NP. The first point we proved a little higher.
The affiliation of this problem to the NP is quite obvious. Recall that a task belongs to the NP class, if the solution to this problem is one of the “yes” or “no” answers, and there is a certificate for the “yes” answer, which allows you to verify that the answer is indeed “yes” in polynomial time. Well, indeed, for the Growing Sakura game, the certificate can be written as a string of length O (n), saving in what order and button we clicked on the corresponding cells, where n is the number of cells in the field. Well, for O (n), you can verify that the certificate is “valid” by simply expanding branches according to the certificate and the rules of the game.
Cheers, Growing Sakura NP is full! If suddenly someone writes a solver for this game that works in polynomial time, you can pick up your million .
Conclusion
The fact that Growing Sakura is NP-complete does not mean that all levels in this game will be prohibitively difficult. It simply means that such levels can be created. And the rest is already dependent on the design levels. Many of the classic Nintendo games are known to be NP-hard, and that doesn’t stop them from enjoying them. Even such a kazualka like Candy Crush is NP-hard , not to mention Tetris , sapper and other sudoku .
Voting on Ludum Dare will end tomorrow, in the update I will publish what place I managed to get. I hope to enter the hundred best games.
Links: game page on Ludum Dare , Dropbox , Itch.io .
UPD. , . Compo 1232 . Growing Sakura 10 ( ). : #4 Theme, #5 Innovation, #22 Fun.
Source: https://habr.com/ru/post/273349/
All Articles