Covering graphs in software testing, part 1

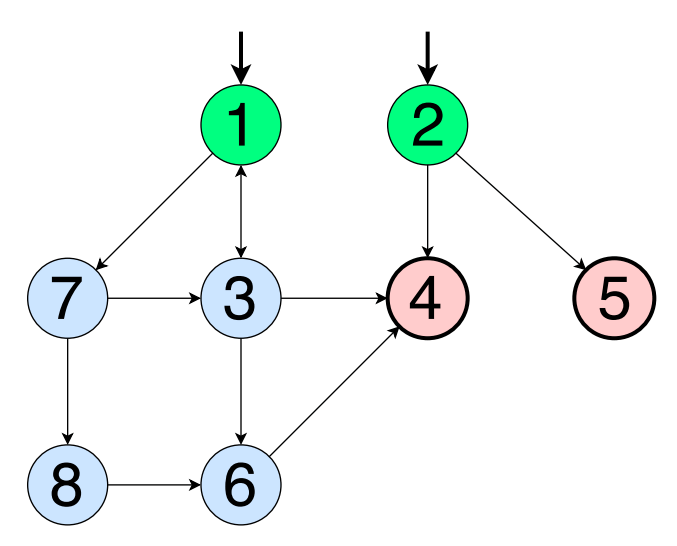
Most programs and algorithms can be represented as a graph consisting of a set of vertices ( N ) and edges ( E ). Coverage of graphs in testing is useful because you can design tests using different coverage criteria and identify errors. With regard to testing the black box, then covering graphs here can also be of great importance if you have to work with states and transitions, entity state graphs, etc. If the graph is rather complicated, different coverage criteria will allow assessing the sufficiency of the test suite.

Definitions

Counts

The formal definition of a graph is given below.

• The graph , G , consists of a set of one or more (1 .. *) vertices, N , and a set of zero and more (0 .. *) edges, .
• An initial set of vertices , N ₀ , and a finite set of vertices , N _f, must be specified. Both of these sets must be non-empty. If the graph consists of one vertex, it must be in both sets, then N ₀ = N _f will be satisfied. Starting vertices are indicated by incoming arrows (see green vertices below). The final vertices are denoted by a bold circle. Below, the colors are used simply for illustration: green - initial, red - final, blue - normal.
• Edge e can combine two vertices, n _p and n _s , where p is the source and s is the receiver. This is represented as (n _p , n _s ) . An edge can also start from one vertex and end at the same vertex: (n, n) .
• A vertex is formally denoted by lowercase n with a numeric index to denote its number. For brevity and ease of understanding, a simplified sittaxis will be used, where the vertex is simply indicated by a number (if there is any uncertainty, we use formal notation). Just keep in mind that the tests may require "long" notation.

Ways in the graph

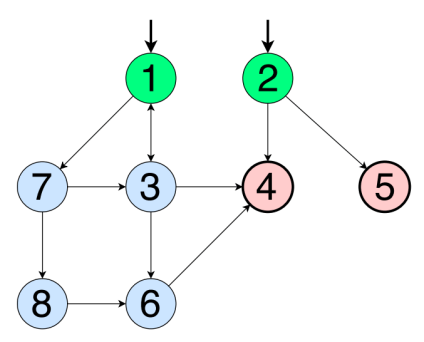
The graph below is for illustrating the definitions given.

')

• Path - a sequence of connected vertices in the graph G. The path p from vertex 1 to 3, 6, and 4 can be written as follows: p = [n ₁ , n ₃ , n ₆ , n ₄ ] (formally). I will write it like this: [1, 3, 6, 4]. The adjacent pairs of vertices in this path are edges. For example, the set of edges in this path is {(1, 3), (3, 6), (6, 4)}. Please note that this is a set of pairs, and I used an informal way of writing (you should also pay attention to the correct placement of parentheses).
• The path length is the number of edges in the path. One vertex has a path of length 0 (it is easy to understand, since, generally speaking, it has 0 edges). Path length p - 3.
• The length of the path - a subset of vertices in the path p . [1, 3] - the segment of the path [1, 3, 6, 4]. Do not confuse this with the edge (1, 3).
• The reach limit (n) can be defined as a subgraph (vertices and edges) that can be reached from vertex n. Reach limit (2) - a set containing vertices 2, 4 and 5. Note that Reach limit () can take as a parameter sets of vertices and edges. The resulting graph is simply the union of all the individual reach limits. For example, the Reach Limit ({6,2}) is the same as the union of the Reach Limit sets (6) and Reach Limit (2). To get this result, list all the vertices that can be reached from vertex 6, and all the vertices that can be reached from vertex 2, merge the lists and remove duplicates. Using the graph above, the result is: {6, 4, 2, 5}. The reach limit ({3, 2}) reaches all vertices and edges in the graph G. You can specify that the reach limit ({2, 3}) = G.
• The test path starts at the starting point and ends at the ending point. Path [1, 3, 4] is the correct test path, and [1, 3, 6] is not. Do you understand why?
• SESE (single-entry, single-exit) columns are columns with one input and one output, i.e. those with exactly one initial and one final vertex.

Vertex Coverage (PV)

The simplest coverage criteria are vertex and edge finishes. Covering the vertices assumes that your tests cover all the reachable vertices in the graph. Requirements for test coverage of vertices in a graph are the set of vertices (N) of a graph.



For this graph, the requirements and the test path satisfying them are given below.

requirements = {1, 2, 3}
path (T) = {[1, 2, 3]}

Rib Coating (PR)

The purpose of covering the edges is to go through all the edges in the graph. An edge can be expressed as a path of length 1. The requirements contain all attainable paths of length up to 1 (and inclusive). The wording “to 1” allows to take into account graphs consisting of one vertex and not having edges.

requirements = {(1, 2), (1, 3), (2, 3)}
path (T) = {[1, 2, 3], [1, 3]}

The tops of the vertices and the edges are most often the same. The exceptions are special cases, including conditional constructions (if-else). (This is the three-vertex graph in the example above: compare the required test paths and see why.)

Paired Rib Coating

Requirements include every reachable path of length up to 2 inclusive.
In fact, find all paths that include three vertices and two edges and create a set of test cases covering these paths. Paths of length 1 will be automatically covered as they will be included in one of these test paths. If there is a path of length 1 that is not a segment of the paths already listed, you need to include it in the list.



In the graph above there are five different pairs of ribs. Pairing the ribs suggests that each of these pairs is covered by at least one test path.

requirements = {[1, 3, 5], [1, 2, 3], [1, 2, 4], [2, 3, 5], [2, 4, 5]}
path (T) = {[1, 3, 5], [1, 2, 3, 5], [1, 2, 4, 5]}

Full track coverage (SPT)

Requirements include all paths in G. This is not possible if there is a cycle in the graph. As a compromise, the covering of established paths is used.

Covering specified paths (PPP)

In the PPP, the requirements are a set of S test paths, where S is the set of paths chosen by the tester. This avoids the problem of having to cover infinitely many paths in the RFP if the graph contains a cycle. In the PPP, the tester simply eliminates the cycle from S , and the requirements of the PPP can be satisfied.



S = {[1, 2, 3], [1, 3], [1, 4, 3]} (All paths in G, except those containing cycles)
requirements = {[1, 2, 3], [1, 3], [1, 4, 3]}
path (T) = {[1, 2, 3], [1, 3], [1, 4, 3]}

SPT impractical. The PPP is a weak compromise to actually satisfy the RFP without adding an infinite set of requirements for graphs with cycles. However, covering the specified paths is also imperfect. A tester can skip important paths when making a set of S , which leads to a subjective and error-resistant MFR.

Attempts to solve this problem have been made for a long time. Starting from a single cycle (1970s), passing each cycle exactly once (1980s) to a less formal description — passing each cycle 0, 1 or more times (1990s), software testers came up with the idea of ​​using basic paths to limit the total number of paths in the graph.

Note in the fields: the cyclomatic complexity of the graph determines the number of tests necessary for all the lines in the program to be executed at least once. Cyclomatic complexity can be calculated by adding 2 to the difference between the number of edges and vertices in the graph.

CA = # edges - # vertices + 2

In the next and last part: the main paths and coverage associated with them.