sin 1 ° on calculator
An important clarification - the calculator is normal, without the sin button. As in accounting or in the market.

Under the cut are three different solutions from different eras, from ancient Samarkand to the United States during the Cold War.
The first thing that comes to mind is the spell:
')
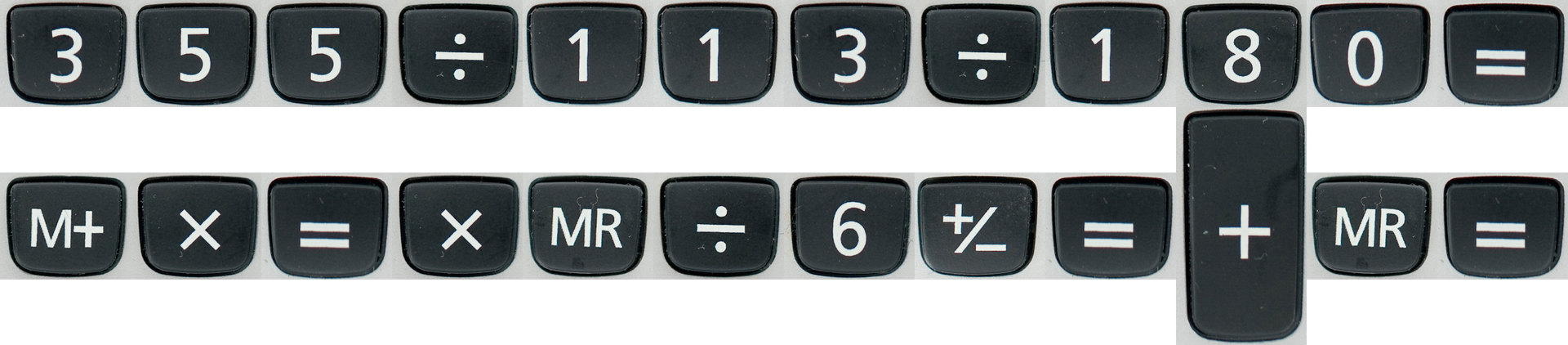
We translate this confused score for a calculator into a more understandable language bc . It is often used as a calculator in the command line of UNIX-like operating systems. We will see something like this:
The above well-known trick appeared only in 1715. Nevertheless, the values of trigonometric functions were known much earlier, and with noticeably greater accuracy.
The head of the Samarkand Observatory, Giyas-ad-Din Jamshid ibn Masood al-Kashi (غیاث الدین جمشید اشانی) compiled tables of trigonometric functions with an accuracy of up to the 16th sign before 1429. Translated from Persian to bc, his spell in relation to our task looked like this:
Note that we still only use addition, subtraction, multiplication, division, and square root. If desired, all these operations can be performed generally on a piece of paper in a column. To count the square root of a column before even taught in school. This is boring, but not very difficult.
An inquisitive reader may have a legitimate question: how does the sine value of a calculator that has such a button count?
It turns out that most calculators use a completely third method - “ figure by figure ”, born in the depths of the US military-industrial complex during the Cold War.

Under the cut are three different solutions from different eras, from ancient Samarkand to the United States during the Cold War.
A simple solution
The first thing that comes to mind is the spell:
')
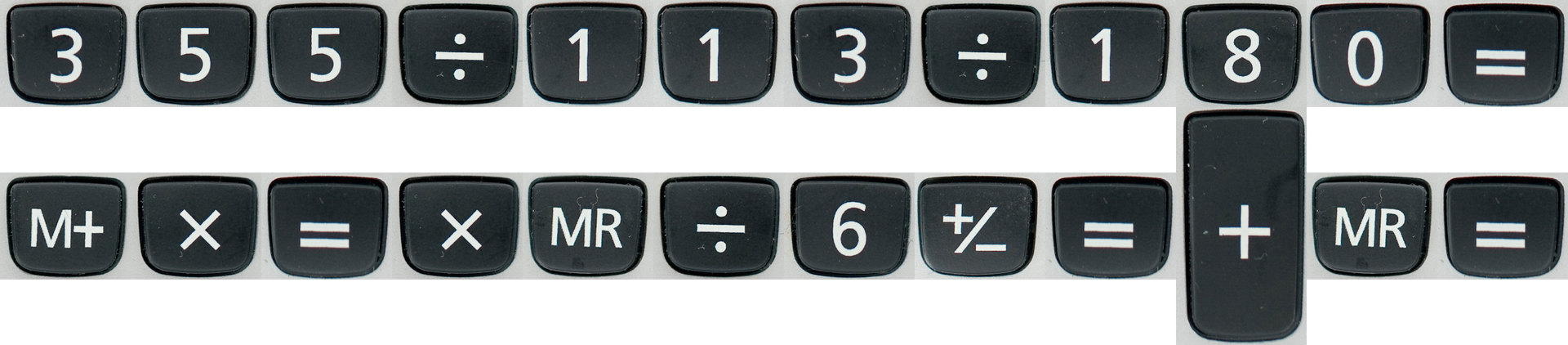
We translate this confused score for a calculator into a more understandable language bc . It is often used as a calculator in the command line of UNIX-like operating systems. We will see something like this:
scale = 7 x = 355/113/180 xx^3/6 .0174524 Where did it come from
We decompose the sine in a row near zero, take the first few members of this series and substitute one degree. In this case, the angle is small, so you can limit yourself to a third degree polynomial:
sin (x) ≅ x - x 3/6
Before substitution, the degree will have to be converted to radians by multiplying by
A separate prize is given to those who noticed strange numbers 355 and 113. They were found in our Chinese comrade Zu Chunzhi (祖 沖 之) during the time of the Qi dynasty (479-502). The ratio of 355/113 is the only approximation of the number
sin (x) ≅ x - x 3/6
Before substitution, the degree will have to be converted to radians by multiplying by
π and dividing by 180 °.A separate prize is given to those who noticed strange numbers 355 and 113. They were found in our Chinese comrade Zu Chunzhi (祖 沖 之) during the time of the Qi dynasty (479-502). The ratio of 355/113 is the only approximation of the number
π rational fraction, which is shorter than the decimal representation of similar accuracy.Interesting decision
The above well-known trick appeared only in 1715. Nevertheless, the values of trigonometric functions were known much earlier, and with noticeably greater accuracy.
The head of the Samarkand Observatory, Giyas-ad-Din Jamshid ibn Masood al-Kashi (غیاث الدین جمشید اشانی) compiled tables of trigonometric functions with an accuracy of up to the 16th sign before 1429. Translated from Persian to bc, his spell in relation to our task looked like this:
scale = 16 sin30 = .5 cos30 = sqrt(3)/2 sin45 = sqrt(2)/2 cos45 = sin45 sin75 = sin30*cos45+cos30*sin45 cos75 = sqrt(1-sin75^2) cos36 = (1+sqrt(5))/4 sin36 = sqrt(1-cos36^2) sin72 = 2*sin36*cos36 cos72 = sqrt(1-sin72^2) (sin3 = sin75*cos72-cos75*sin72) .0523359562429430 (x = sin3/3) .0174453187476476 (x = (sin3+4*x^3)/3) .0174523978055315 (x = (sin3+4*x^3)/3) .0174524064267667 (x = (sin3+4*x^3)/3) .0174524064372703 (x = (sin3+4*x^3)/3) .0174524064372831 (x = (sin3+4*x^3)/3) .0174524064372831 Note that we still only use addition, subtraction, multiplication, division, and square root. If desired, all these operations can be performed generally on a piece of paper in a column. To count the square root of a column before even taught in school. This is boring, but not very difficult.
What is this shamanism
Let's sort out the al-Kashi magic in steps.
Sine and cosine 30 ° and 45 ° were known to the ancient Greeks.
There is a sine sum of angles of 30 ° and 45 °. Before al-Kashi, this formula was derived by another Persian astronomer, Abul-Wafa Muhammad ibn Muhammad ibn Yahya ibn Ismail ibn Abbas al-Buzdjani.
Pythagorean pants are equal in all directions.
This is from a regular pentagon, known even to the ancient Greeks.
Again the sine sum and the Pythagorean theorem.
We consider the sine of the difference 75 ° and 72 ° and we get the sine of 3 °.
Now you can expand 3 ° to the sum of three angles of 1 °, but a hitch occurs - we get a cubic equation:
sin 3 ° = 3 x - 4 x 3
where x = sin 1 °. Solving cubic equations analytically then no one else knew how.
The wise al-Kashi remarked that one can express this equation in the following form:
f (x) = (sin 3 ° + 4 x 3 ) / 3
and then apply a simple iteration method to f (x). I remind you that at that time neither Newton nor Raphson were yet born.
First approach.
We get 16 characters after five iterations.
sin30 = .5 cos30 = sqrt(3)/2 sin45 = sqrt(2)/2 cos45 = sin45 Sine and cosine 30 ° and 45 ° were known to the ancient Greeks.
sin75 = sin30*cos45+cos30*sin45 There is a sine sum of angles of 30 ° and 45 °. Before al-Kashi, this formula was derived by another Persian astronomer, Abul-Wafa Muhammad ibn Muhammad ibn Yahya ibn Ismail ibn Abbas al-Buzdjani.
cos75 = sqrt(1-sin75^2) Pythagorean pants are equal in all directions.
cos36 = (1+sqrt(5))/4 sin36 = sqrt(1-cos36^2) This is from a regular pentagon, known even to the ancient Greeks.
sin72 = 2*sin36*cos36 cos72 = sqrt(1-sin72^2) Again the sine sum and the Pythagorean theorem.
(sin3 = sin75*cos72-cos75*sin72) .0523359562429430 We consider the sine of the difference 75 ° and 72 ° and we get the sine of 3 °.
Now you can expand 3 ° to the sum of three angles of 1 °, but a hitch occurs - we get a cubic equation:
sin 3 ° = 3 x - 4 x 3
where x = sin 1 °. Solving cubic equations analytically then no one else knew how.
The wise al-Kashi remarked that one can express this equation in the following form:
f (x) = (sin 3 ° + 4 x 3 ) / 3
and then apply a simple iteration method to f (x). I remind you that at that time neither Newton nor Raphson were yet born.
(x = sin3/3) First approach.
.0174453187476476 (x = (sin3+4*x^3)/3) .0174523978055315 (x = (sin3+4*x^3)/3) .0174524064267667 (x = (sin3+4*x^3)/3) .0174524064372703 (x = (sin3+4*x^3)/3) .0174524064372831 (x = (sin3+4*x^3)/3) .0174524064372831 We get 16 characters after five iterations.
According to the calculator itself
An inquisitive reader may have a legitimate question: how does the sine value of a calculator that has such a button count?
It turns out that most calculators use a completely third method - “ figure by figure ”, born in the depths of the US military-industrial complex during the Cold War.
And here the bomber B-58
Jack Walder came up with this algorithm, who then worked for Convair on the navigation calculator of the aforementioned bomber.
The main advantage of the “digit by digit” method is that it uses only the operations of addition and division by two (which is easy to implement by shifting to the right).
In addition, the algorithm can be made to work directly in the binary-decimal code, which is used in most calculators, but in the example below, we will not get into this jungle.
The algorithm is iterative and uses an arc tangent table, one per iteration. The table must be calculated in advance:
At the same time is considered the scaling factor
After that, you can calculate the notorious sin 1 ° as follows:
Result:
There are 32 iterations, so a small error remains. Calculators typically use 40 iterations.
The main advantage of the “digit by digit” method is that it uses only the operations of addition and division by two (which is easy to implement by shifting to the right).
In addition, the algorithm can be made to work directly in the binary-decimal code, which is used in most calculators, but in the example below, we will not get into this jungle.
The algorithm is iterative and uses an arc tangent table, one per iteration. The table must be calculated in advance:
#include <stdio.h> #include <math.h> int main(int argc, char **argv) { int bits = 32; int cordic_one = 1 << (bits - 2); printf("// , \n"); printf("static const int cordic_one = 0x%08x;\n", cordic_one); printf("static const int cordic_table[] = {\n"); double k = 1; for (int i = 0; i < bits; i++) { printf("0x%08x, // 0x%08x * atan(1/%.0f) \n", (int)(atan(pow(2, -i)) * cordic_one), cordic_one, pow(2, i)); k /= sqrt(1 + pow(2, -2 * i)); } printf("};\n"); printf("static const int cordic_k = 0x%08x; // %.16f * 0x%08x\n", (int)(k * cordic_one), k, cordic_one); } At the same time is considered the scaling factor
cordic_k .After that, you can calculate the notorious sin 1 ° as follows:
#include <stdio.h> #include <math.h> // , static const int cordic_one = 0x40000000; static const int cordic_table[] = { 0x3243f6a8, // 0x40000000 * atan(1/1) 0x1dac6705, // 0x40000000 * atan(1/2) 0x0fadbafc, // 0x40000000 * atan(1/4) 0x07f56ea6, // 0x40000000 * atan(1/8) 0x03feab76, // 0x40000000 * atan(1/16) 0x01ffd55b, // 0x40000000 * atan(1/32) 0x00fffaaa, // 0x40000000 * atan(1/64) 0x007fff55, // 0x40000000 * atan(1/128) 0x003fffea, // 0x40000000 * atan(1/256) 0x001ffffd, // 0x40000000 * atan(1/512) 0x000fffff, // 0x40000000 * atan(1/1024) 0x0007ffff, // 0x40000000 * atan(1/2048) 0x0003ffff, // 0x40000000 * atan(1/4096) 0x0001ffff, // 0x40000000 * atan(1/8192) 0x0000ffff, // 0x40000000 * atan(1/16384) 0x00007fff, // 0x40000000 * atan(1/32768) 0x00003fff, // 0x40000000 * atan(1/65536) 0x00001fff, // 0x40000000 * atan(1/131072) 0x00000fff, // 0x40000000 * atan(1/262144) 0x000007ff, // 0x40000000 * atan(1/524288) 0x000003ff, // 0x40000000 * atan(1/1048576) 0x000001ff, // 0x40000000 * atan(1/2097152) 0x000000ff, // 0x40000000 * atan(1/4194304) 0x0000007f, // 0x40000000 * atan(1/8388608) 0x0000003f, // 0x40000000 * atan(1/16777216) 0x0000001f, // 0x40000000 * atan(1/33554432) 0x0000000f, // 0x40000000 * atan(1/67108864) 0x00000008, // 0x40000000 * atan(1/134217728) 0x00000004, // 0x40000000 * atan(1/268435456) 0x00000002, // 0x40000000 * atan(1/536870912) 0x00000001, // 0x40000000 * atan(1/1073741824) 0x00000000, // 0x40000000 * atan(1/2147483648) }; static const int cordic_k = 0x26dd3b6a; // 0.6072529350088813 * 0x40000000 void cordic(int theta, int& s, int& c) { c = cordic_k; s = 0; for (int k = 0; k < 32; ++k) { int d = (theta >= 0) ? 0 : -1; int tx = c - (((s >> k) ^ d) - d); int ty = s + (((c >> k) ^ d) - d); c = tx; s = ty; theta -= ((cordic_table[k] ^ d) - d); } } int main(void) { double alpha = M_PI / 180; int sine, cosine; cordic(alpha * cordic_one, sine, cosine); printf("CORDIC: %.8f\nExpected: %.8f\n", (double)sine / cordic_one, sin(alpha)); } Result:
CORDIC: 0.01745240 Expected: 0.01745241 There are 32 iterations, so a small error remains. Calculators typically use 40 iterations.
Source: https://habr.com/ru/post/271889/
All Articles