Gravitational field on the surface of bodies of irregular shape on the example of the comet Churyumov-Gerasimenko
It is known from the law of world wideness that on the surface of spherical bodies the acceleration of free fall is constant in magnitude and is directed to the center of the ball. For bodies of irregular shape, this rule is obviously not satisfied. In this article I will show the method of calculating and visualizing the acceleration of free fall for such bodies. The calculation will be done in JavaScript, visualized - in WebGL using the library three.js .
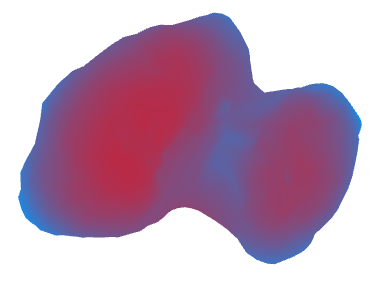
As a result, we get the following (in red, areas with high acceleration of gravity are marked, blue - with small):
To calculate the gravitational potential of the planets, the following formula is used :

But, unfortunately, at small r, this series converges slowly, and at very small r, it generally diverges. Therefore, this formula is not suitable for calculating the gravitational potential on the surface of celestial bodies. In general, it is necessary to integrate over the entire volume of the body.
A three-dimensional body can be represented as a set of triangular faces, with given coordinates of the vertices. Further we will assume that the density of the body is constant (for a comet, this approximately corresponds to the truth). The gravitational potential at a given point will be equal to the sum of the potentials of all tetrahedra, with a base in these faces and with a vertex at a given point (we are not looking for the gravitational potential, but the gravitational acceleration, which is the potential gradient, but the reasoning remains the same).
First we need to find the acceleration that the mass of the tetrahedron produces to the point at its top. To do this, integrate over the entire volume of the tetrahedron. Unfortunately, this integral is not taken in elementary functions, so you have to go for a trick.
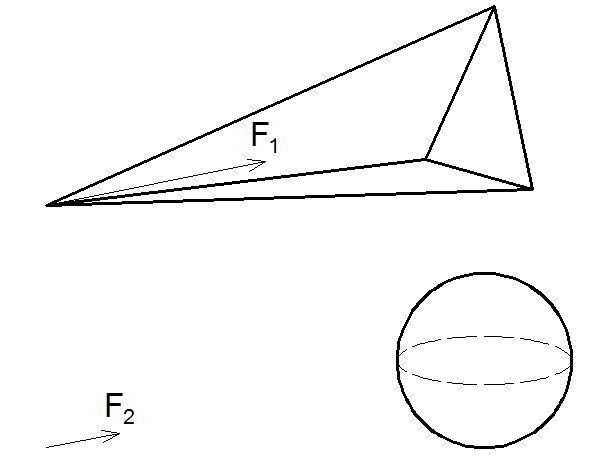
The force acting on a point at the top of a tetrahedron is approximately three times greater than the force caused by the gravity of a ball placed in the middle of the base of the tetrahedron (the mass of the ball is equal to the mass of the tetrahedron). That is, F 1 ≈3 * F 2 . This equality is better fulfilled with a small angle of the tetrahedron solution. To estimate the value of the deviation of equality from the strict one, I generated several thousand random tetrahedra and calculated this value for them.

The graph on the abscissa axis shows the ratio of the perimeter of the triangular base to the distance from the top to the center of the base. The ordinate is the magnitude of the error. As you can see, the magnitude of the error can be represented by a quadratic function. With rare exceptions, all points are below the parabola (exceptions will not spoil the weather for us).
The magnitude of the gravitational acceleration will be calculated with a given relative error. If the calculation error exceeds this error, then we divide our tetrahedron into four parts along the base and calculate the acceleration for these parts separately, then sum it up.
Acceleration we find up to a certain constant, for a given body, a coefficient depending on the mass (or density) of the body, the gravitational constant, and some other parameters. We will take this factor into account later.
We calculate the acceleration from a three-dimensional body by summing over all tetrahedra formed by the edges of the body and a given point (which I wrote earlier).
We calculate the gravitational and centrifugal accelerations on the comet (the rotation of the comet causes an acceleration of about 25% of the gravitational acceleration, therefore, it cannot be neglected). I set the relative error to 0.01. It would seem a lot, but in fact, the error is calculated three times less and the difference is not noticeable when visualizing (since the minimum difference in the color of the pixels is 1 / 256≈0.004). And if you set the error less, the calculation time increases.
With an error of 0.01, the calculation is performed for 1-2 seconds, so we make it through setInterval, in order to avoid browser hangs.
Now it's worth talking about the format of working with a 3D body. It's simple. This is an object consisting of three arrays: vertices, normals, and triangular faces.
A vertex array stores vertex coordinate objects. The array of normals is the vertex normal vectors. An array of faces is an array of three numbers that store vertex numbers.
I downloaded the model of comet Churyumov-Gerasimenko from the ESA website and simplified it in 3Ds Max. In the original model there were several tens of thousands of vertices and faces, but for our task this is too much, because the computational complexity of the algorithm depends on the product of the number of vertices and the number of faces. The model is saved in obj format.
In the library three.js there is an OBJLoader function for loading this format, but only the information about the vertices remains at loading, and the information about the faces is lost, which is not suitable for our task. Therefore, I modified it somewhat.
So, we loaded the object from the file, then we calculated the acceleration vector at each of its vertices, now we need to visualize it. To do this, you need to create a scene, adjust the camera and the light, add and color our model.
The scene is created simply.
There are no problems with the camera either.
To create a camera, we used the THREE.PerspectiveCamera function (fov, aspect, near, far), where:
fov is the height of the field of view of the camera in degrees;
aspect - the ratio of the horizontal angle of view of the camera to the vertical;
near - distance to the near plane (the one that is closer will not be rendered);
far - distance to the far plan.
We put the light.
Create a visualizer.
For working with models in three.js it is convenient to use the BufferGeometry class.
We set the material.
Load the vertex coordinates.
Calculate the color of the vertices.
We will also need to display the directions of the acceleration of free fall at each vertex.
With visualization finished. We look what happened.
Demo 1 .
As we see, the acceleration of free fall on a comet is from 40 to 80 thousand times less than on Earth. The maximum deviation of the acceleration vector from the normal is about 60-70 degrees. Small and large stones in these areas probably do not linger and slowly roll into areas where the angle is not so large.
You can play with the bodies of another form. Demo 2 .
We see that for a cube the maximum acceleration (in the center of the face) is 1.002 acceleration for a ball of the same mass, but in fact this value is slightly less than one (what we considered with a relative error of 0.01 played a role). For a cube, unlike a tetrahedron, there are exact formulas for calculating accelerations and the exact value for the center of the face is (for a cube with a side equal to 1):
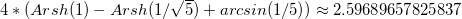
For a ball of the same volume:
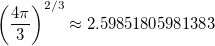
Their ratio is 0.999376 and only slightly less than one.
In conclusion, the question. Are there any bodies that have at least one point the ratio of the absolute value of the gravitational acceleration to the acceleration on the surface of the ball of the same mass and volume greater than one? If so, for which body is this relationship maximal? How many times is this ratio greater than one, at times or by percent?
As a result, we get the following (in red, areas with high acceleration of gravity are marked, blue - with small):

Gif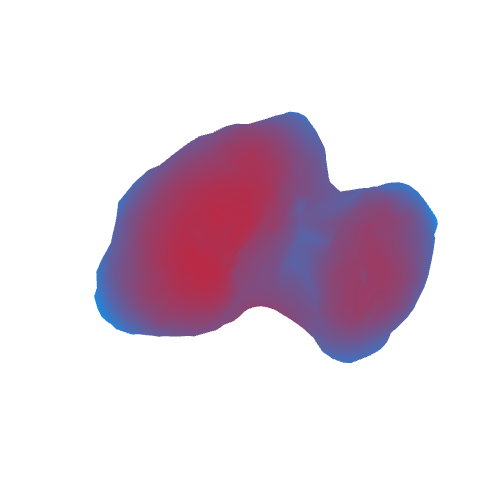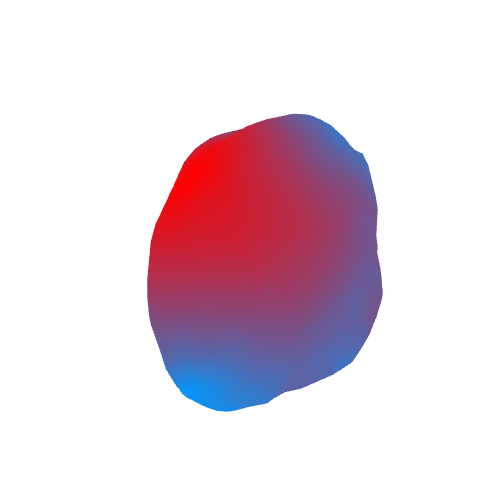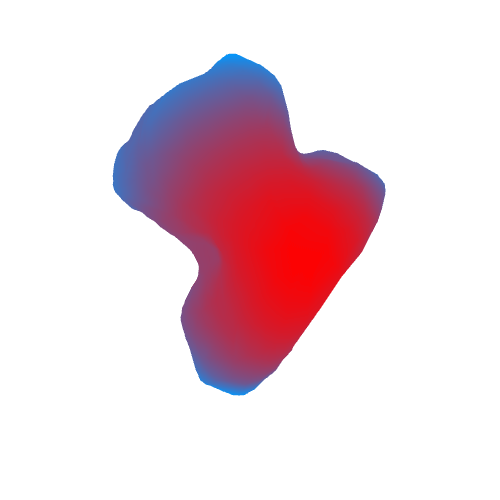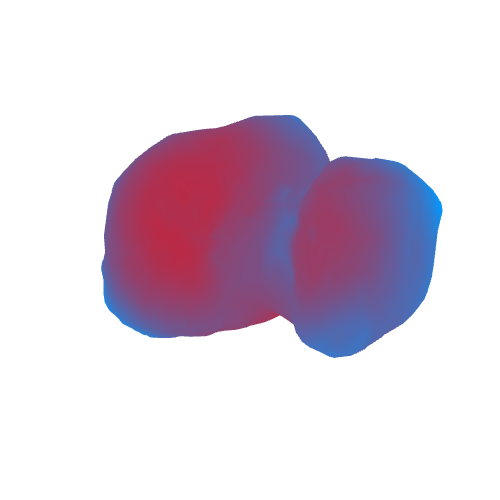
')
The axis of rotation on the gif is conditional. It does not coincide with the axis of rotation of the comet.
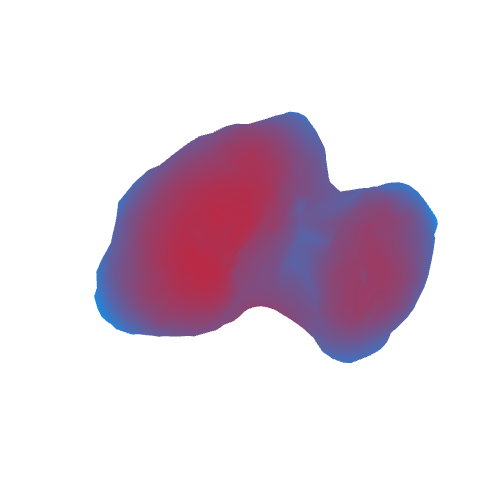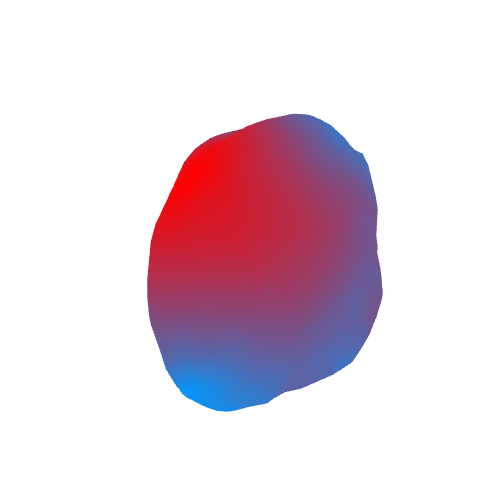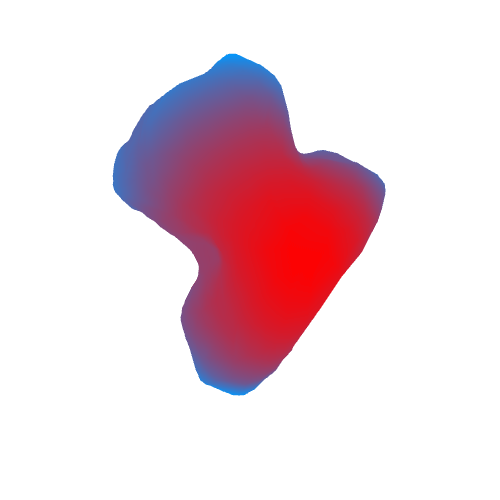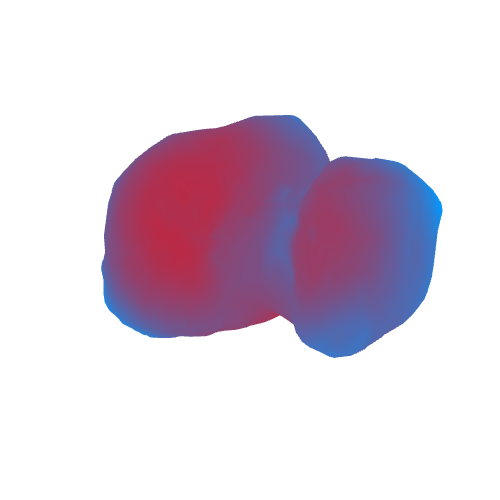
')
The axis of rotation on the gif is conditional. It does not coincide with the axis of rotation of the comet.
To calculate the gravitational potential of the planets, the following formula is used :

But, unfortunately, at small r, this series converges slowly, and at very small r, it generally diverges. Therefore, this formula is not suitable for calculating the gravitational potential on the surface of celestial bodies. In general, it is necessary to integrate over the entire volume of the body.
A three-dimensional body can be represented as a set of triangular faces, with given coordinates of the vertices. Further we will assume that the density of the body is constant (for a comet, this approximately corresponds to the truth). The gravitational potential at a given point will be equal to the sum of the potentials of all tetrahedra, with a base in these faces and with a vertex at a given point (we are not looking for the gravitational potential, but the gravitational acceleration, which is the potential gradient, but the reasoning remains the same).
First we need to find the acceleration that the mass of the tetrahedron produces to the point at its top. To do this, integrate over the entire volume of the tetrahedron. Unfortunately, this integral is not taken in elementary functions, so you have to go for a trick.

The force acting on a point at the top of a tetrahedron is approximately three times greater than the force caused by the gravity of a ball placed in the middle of the base of the tetrahedron (the mass of the ball is equal to the mass of the tetrahedron). That is, F 1 ≈3 * F 2 . This equality is better fulfilled with a small angle of the tetrahedron solution. To estimate the value of the deviation of equality from the strict one, I generated several thousand random tetrahedra and calculated this value for them.

The graph on the abscissa axis shows the ratio of the perimeter of the triangular base to the distance from the top to the center of the base. The ordinate is the magnitude of the error. As you can see, the magnitude of the error can be represented by a quadratic function. With rare exceptions, all points are below the parabola (exceptions will not spoil the weather for us).
The magnitude of the gravitational acceleration will be calculated with a given relative error. If the calculation error exceeds this error, then we divide our tetrahedron into four parts along the base and calculate the acceleration for these parts separately, then sum it up.

Acceleration we find up to a certain constant, for a given body, a coefficient depending on the mass (or density) of the body, the gravitational constant, and some other parameters. We will take this factor into account later.
The time has come for the code
function force_pyramide(p1, p2, p3, rel) { // (0, 0, 0) // rel - var volume = (1/6) * triple_product(p1, p2, p3); // if (volume == 0) return new vector3(0, 0, 0); if (!rel) rel = 0.01; var p0 = middleVector(p1, p2, p3); // var len = p0.length(); var per = perimeter(p1, p2, p3); // var tan_per = per / len; var error = 0.015 * sqr(tan_per); // if (error > rel) { var p12 = middleVector(p1, p2); var p13 = middleVector(p1, p3); var p23 = middleVector(p2, p3); return sumVector( force_pyramide(p1, p12, p13, rel), force_pyramide(p2, p23, p12, rel), force_pyramide(p3, p13, p23, rel), force_pyramide(p12, p23, p13, rel) ); } var ratio = 3 * volume * Math.pow(len, -3); return new vector3(p0.x, p0.y, p0.z).multiplyScalar(ratio); } We calculate the acceleration from a three-dimensional body by summing over all tetrahedra formed by the edges of the body and a given point (which I wrote earlier).
Hidden text
function force_object(p0, obj, rel) { var result = new vector3(0, 0, 0); for (var i = 0; i < obj.faces.length; i++) { p1 = subVectors(obj.vertices[obj.faces[i][0] - 1], p0); p2 = subVectors(obj.vertices[obj.faces[i][1] - 1], p0); p3 = subVectors(obj.vertices[obj.faces[i][2] - 1], p0); var f = force_pyramide(p1, p2, p3, rel); result = addVectors(result, f); } return result; } We calculate the gravitational and centrifugal accelerations on the comet (the rotation of the comet causes an acceleration of about 25% of the gravitational acceleration, therefore, it cannot be neglected). I set the relative error to 0.01. It would seem a lot, but in fact, the error is calculated three times less and the difference is not noticeable when visualizing (since the minimum difference in the color of the pixels is 1 / 256≈0.004). And if you set the error less, the calculation time increases.
With an error of 0.01, the calculation is performed for 1-2 seconds, so we make it through setInterval, in order to avoid browser hangs.
Code
var rel = 0.01; // var scale = 1000; // , var grav_ratio = 6.672e-11 * 1.0e+13 / (sqr(scale) * volume); // 1+13 var omega2 = sqr(2 * Math.PI / (12.4 * 3600)); // 12,4 function computeGrav() { info.innerHTML = ': ' + (100 * item / object3d.vertices.length).toFixed() + '%'; for (var i = 0; i < 50; i++) { var p0 = object3d.vertices[item]; grav_force[item] = force_object(p0, object3d, rel).multiplyScalar(grav_ratio); // circular_force[item] = new vector3(omega2 * p0.x * scale, omega2 * p0.y * scale, 0); // , z abs_grav_force[item] = grav_force[item].length(); abs_circular_force[item] = circular_force[item].length(); item++; if (item >= object3d.vertices.length) { console.timeEnd('gravity calculate'); clearInterval(timerId); accelSelect(); init(); animate(); break; } } } var item = 0; console.time('gravity calculate'); var timerId = setInterval(computeGrav, 1); Now it's worth talking about the format of working with a 3D body. It's simple. This is an object consisting of three arrays: vertices, normals, and triangular faces.
var obj = { vertices: [], normals: [], faces: [] }; A vertex array stores vertex coordinate objects. The array of normals is the vertex normal vectors. An array of faces is an array of three numbers that store vertex numbers.
I downloaded the model of comet Churyumov-Gerasimenko from the ESA website and simplified it in 3Ds Max. In the original model there were several tens of thousands of vertices and faces, but for our task this is too much, because the computational complexity of the algorithm depends on the product of the number of vertices and the number of faces. The model is saved in obj format.
In the library three.js there is an OBJLoader function for loading this format, but only the information about the vertices remains at loading, and the information about the faces is lost, which is not suitable for our task. Therefore, I modified it somewhat.
Code
function objLoad(url) { var result; var xhr = new XMLHttpRequest(); xhr.open('GET', url, false); xhr.onreadystatechange = function(){ if (xhr.readyState != 4) return; if (xhr.status != 200) { result = xhr.status + ': ' + xhr.statusText + ': ' + xhr.responseText; } else { result = xhr; } } xhr.send(null); return result; } function objParse(url) { var txt = objLoad(url).responseText; var lines = txt.split('\n'); var result; // v float float float var vertex_pattern = /v( +[\d|\.|\+|\-|e|E]+)( +[\d|\.|\+|\-|e|E]+)( +[\d|\.|\+|\-|e|E]+)/; // f vertex vertex vertex ... var face_pattern1 = /f( +-?\d+)( +-?\d+)( +-?\d+)( +-?\d+)?/; // f vertex/uv vertex/uv vertex/uv ... var face_pattern2 = /f( +(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+))?/; // f vertex/uv/normal vertex/uv/normal vertex/uv/normal ... var face_pattern3 = /f( +(-?\d+)\/(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+)\/(-?\d+))?/; // f vertex//normal vertex//normal vertex//normal ... var face_pattern4 = /f( +(-?\d+)\/\/(-?\d+))( +(-?\d+)\/\/(-?\d+))( +(-?\d+)\/\/(-?\d+))( +(-?\d+)\/\/(-?\d+))?/; var obj = { vertices: [], normals: [], faces: [] }; for (var i = 0; i < lines.length; i++) { var line = lines[i].trim(); if ((result = vertex_pattern.exec(line)) !== null) { obj.vertices.push(new vector3( parseFloat(result[1]), parseFloat(result[2]), parseFloat(result[3]) )); }else if ((result = face_pattern1.exec(line)) !== null) { obj.faces.push([ parseInt(result[1]), parseInt(result[2]), parseInt(result[3]) ]); if (result[4]) obj.faces.push([ parseInt(result[1]), parseInt(result[3]), parseInt(result[4]) ]); }else if ((result = face_pattern2.exec(line)) !== null) { obj.faces.push([ parseInt(result[2]), parseInt(result[5]), parseInt(result[8]) ]); if (result[11]) obj.faces.push([ parseInt(result[2]), parseInt(result[8]), parseInt(result[11]) ]); }else if ((result = face_pattern3.exec(line)) !== null) { obj.faces.push([ parseInt(result[2]), parseInt(result[6]), parseInt(result[10]) ]); if (result[14]) obj.faces.push([ parseInt(result[2]), parseInt(result[10]), parseInt(result[14]) ]); }else if ((result = face_pattern4.exec(line)) !== null) { obj.faces.push([ parseInt(result[2]), parseInt(result[5]), parseInt(result[8]) ]); if (result[11]) obj.faces.push([ parseInt(result[2]), parseInt(result[8]), parseInt(result[11]) ]); } } obj.normals = computeNormalizeNormals(obj); return obj; } So, we loaded the object from the file, then we calculated the acceleration vector at each of its vertices, now we need to visualize it. To do this, you need to create a scene, adjust the camera and the light, add and color our model.
The scene is created simply.
scene = new THREE.Scene(); There are no problems with the camera either.
var fieldWidth = 500; // var fieldHeight = 500; camera = new THREE.PerspectiveCamera(50, fieldWidth / fieldHeight, 0.01, 10000); scene.add(camera); cameraZ = 3 * boundingSphereRadius; // boundingSphereRadius - , camera.position.x = 0; camera.position.y = 0; camera.position.z = cameraZ; camera.lookAt(new THREE.Vector3(0, 0, 0)); // To create a camera, we used the THREE.PerspectiveCamera function (fov, aspect, near, far), where:
fov is the height of the field of view of the camera in degrees;
aspect - the ratio of the horizontal angle of view of the camera to the vertical;
near - distance to the near plane (the one that is closer will not be rendered);
far - distance to the far plan.
We put the light.
var ambientLight = new THREE.AmbientLight(0xffffff); scene.add(ambientLight); Create a visualizer.
renderer = new THREE.WebGLRenderer({antialias: true}); renderer.setClearColor(0xffffff); // renderer.setPixelRatio(window.devicePixelRatio); renderer.setSize(fieldWidth, fieldHeight); // container.appendChild(renderer.domElement); // Together
var container; var camera, scene, renderer; var axis; var mesh; var boundingSphereRadius, cameraZ; var lines = []; var angleGeneral = 0; function init() { container = document.getElementById('container'); scene = new THREE.Scene(); var fieldWidth = 500; var fieldHeight = 500; camera = new THREE.PerspectiveCamera(50, fieldWidth / fieldHeight, 0.01, 10000); scene.add(camera); var ambientLight = new THREE.AmbientLight(0xffffff); scene.add(ambientLight); loadModel(); cameraZ = 3 * boundingSphereRadius; camera.position.x = 0; camera.position.y = 0; camera.position.z = cameraZ; camera.lookAt(new THREE.Vector3(0, 0, 0)); axis = new THREE.Vector3(0.6, 0.8, 0); // renderer = new THREE.WebGLRenderer({antialias: true}); renderer.setClearColor(0xffffff); renderer.setPixelRatio(window.devicePixelRatio); renderer.setSize(fieldWidth, fieldHeight); container.appendChild(renderer.domElement); } For working with models in three.js it is convenient to use the BufferGeometry class.
var geometry = new THREE.BufferGeometry(); We set the material.
var material = new THREE.MeshLambertMaterial( { side: THREE.FrontSide, // vertexColors: THREE.VertexColors // }); Load the vertex coordinates.
var vertices = new Float32Array(9 * object3d.faces.length); for (var i = 0; i < object3d.faces.length; i++) { for (var j = 0; j < 3; j++) { vertices[9*i + 3*j ] = object3d.vertices[object3d.faces[i][j] - 1].x; vertices[9*i + 3*j + 1] = object3d.vertices[object3d.faces[i][j] - 1].y; vertices[9*i + 3*j + 2] = object3d.vertices[object3d.faces[i][j] - 1].z; } } geometry.addAttribute('position', new THREE.BufferAttribute(vertices, 3)); Calculate the color of the vertices.
var colors = addColor(); geometry.addAttribute('color', new THREE.BufferAttribute(colors, 3)); function addColor() { var colorMin = [0.0, 0.6, 1.0]; // var colorMax = [1.0, 0.0, 0.0]; // var colors = new Float32Array(9 * object3d.faces.length); for (var i = 0; i < object3d.faces.length; i++) { for (var j = 0; j < 3; j++) { var intensity = (abs_force[object3d.faces[i][j] - 1] - forceMin) / (forceMax - forceMin); colors[9*i + 3*j ] = colorMin[0] + (colorMax[0] - colorMin[0]) * intensity; colors[9*i + 3*j + 1] = colorMin[1] + (colorMax[1] - colorMin[1]) * intensity; colors[9*i + 3*j + 2] = colorMin[2] + (colorMax[2] - colorMin[2]) * intensity; } } return colors; } We will also need to display the directions of the acceleration of free fall at each vertex.
Code
var lines; function addLines() { lines = new Array(); for (var i = 0; i < object3d.vertices.length; i++) { var color; var ratio; if (angle_force[i] < 90) { color = 0x000000; // ratio = -0.2 * boundingSphereRadius / forceMax; } else { color = 0xdddddd; // ratio = 0.2 * boundingSphereRadius / forceMax; } var material = new THREE.LineBasicMaterial({ color: color }); var geometry = new THREE.Geometry(); var point1 = object3d.vertices[i]; var point2 = new THREE.Vector3(); point2.copy(force[i]); point2.addVectors(point1, point2.multiplyScalar(ratio)); geometry.vertices.push( new THREE.Vector3(point1.x, point1.y, point1.z), new THREE.Vector3(point2.x, point2.y, point2.z) ); var line = new THREE.Line(geometry, material); rotateAroundWorldAxis(line, axis, angleGeneral); if (hair.checked) scene.add(line); lines.push(line); } } With visualization finished. We look what happened.
Demo 1 .
As we see, the acceleration of free fall on a comet is from 40 to 80 thousand times less than on Earth. The maximum deviation of the acceleration vector from the normal is about 60-70 degrees. Small and large stones in these areas probably do not linger and slowly roll into areas where the angle is not so large.
You can play with the bodies of another form. Demo 2 .
We see that for a cube the maximum acceleration (in the center of the face) is 1.002 acceleration for a ball of the same mass, but in fact this value is slightly less than one (what we considered with a relative error of 0.01 played a role). For a cube, unlike a tetrahedron, there are exact formulas for calculating accelerations and the exact value for the center of the face is (for a cube with a side equal to 1):
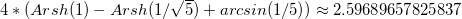
For a ball of the same volume:
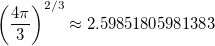
Their ratio is 0.999376 and only slightly less than one.
In conclusion, the question. Are there any bodies that have at least one point the ratio of the absolute value of the gravitational acceleration to the acceleration on the surface of the ball of the same mass and volume greater than one? If so, for which body is this relationship maximal? How many times is this ratio greater than one, at times or by percent?
Source: https://habr.com/ru/post/271451/
All Articles