Assembling a 4-dimensional Rubik's Cube
We are familiar with the Rubik's cube puzzle, but, living in three-dimensional space, it is difficult to imagine such in four-dimensional. Of course, Rubik did not patent four-dimensional cubes, and we are talking only about the similarity of the Rubik's cube.
Therefore, first I will talk about how I imagine a four-dimensional puzzle.
To begin with, imagine how a three-dimensional cube is obtained. Let's take one-dimensional space: everything that we can depict in it is limited to one-dimensional objects, such as a point, a segment, a ray, a straight line. Draw a segment of unit length AB [0,1]. Now we will add the second dimension: the ordinate axis will be directed upwards, and our unit segment AB lies on the x-axis, in the Cartesian coordinate system.
')
Perhaps the two-dimensional space is most familiar to human understanding, because neither the sphere, nor the cube, will not work, we are accustomed to depict them as a projection on a plane. Well, with two-dimensional space, we have no problems, so let's think about how to get a square. So, we take the segment AB (vertices A (0,0) and B (1,0)) on the abscissa axis, retreat exactly one on the ordinate axis and duplicate the segment, let's call it CD, with points C (0,1) and D (1,1).
To get a square, we now need to connect the corresponding vertices, that is, connect the vertex A (0,0) with its duplicate C (0,1), and connect the vertex B (1,0) with D (1,1). Now we have an ACDB square. Having understood how it works in two-dimensional space, it will be quite easy to understand how a cube is made in three-dimensional. So the points:
1. Add the third dimension, the axis of applicat will be directed into depth.
2. Duplicate ACDB by retreating by one along the axis of applicate, the vertices are transformed as follows:
A (0,0,0) -> H (0,0,1)
C (0,1,0) -> F (0,1,1)
D (1,1,0) -> G (1,1,1)
B (1,0,0) -> E (1,0,1)
3. Connect the corresponding vertices of the squares.
Now the reader is mentally prepared to see the tesseract:
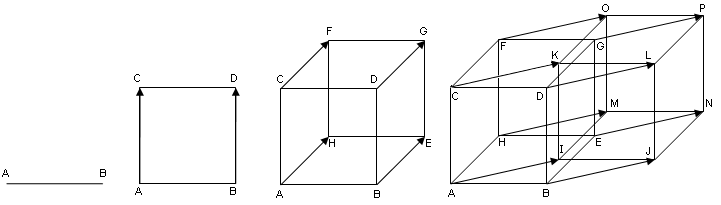
In fact, we duplicate the cube, shifting along the axis of the fourth dimension, and connect the corresponding vertices - you can’t think of something easier. For clarity, we will increase the duplicate cube by placing the original cube inside it. This image is most often used when trying to project a tesseract onto a plane:

To emphasize that all the segments at tesseract are single and to show equal projection, the 4-D cube can be animated:

But this is all a saying, and the tale is ahead!
Now let's see what there is a four-dimensional puzzle, and most importantly how to portray it.
As is known, a cube has six faces, therefore, a three-dimensional puzzle of 6 colors. To simplify our life, we will work with a 2x2x2 cube, in particular, it will be very useful for us that the permutations of such a cube are only 3 ^ 6 * 7! = 3674160.

We list the faces:
- On the abscissa axis Left-Right, color green-blue.
- On the y-axis Down-Up, color yellow-white.
- On the axis of the front-back applique, color red-orange.
Turn on the warp drive and open the wormhole in the fourth dimension!
This is how foreign mathematicians depict a four-dimensional puzzle:
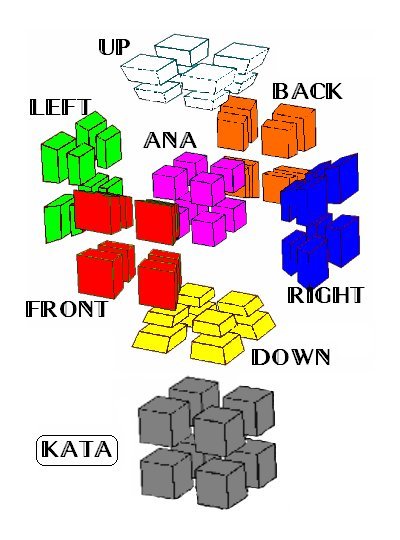
That is, in fact, we just took a three-dimensional cube 2x2x2, added an axis to the fourth dimension and got the fourth line:
- Along the axis of the fourth dimension Ana-Kata, color purple-gray.
It should be noted that now all groups of 8 colors are three-dimensional facets, and not two-dimensional faces (which had 4 colors each). Now, how to imagine exactly the same (mathematically equivalent) four-dimensional cube I:

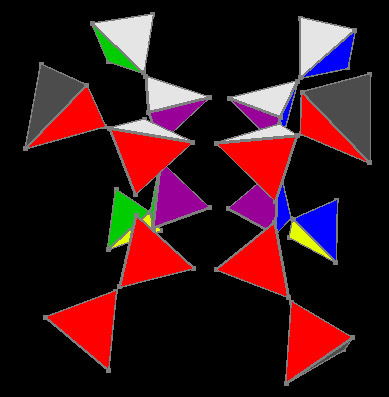
If we take the inner part of the puzzle (that is, the cube consisting of 8 three-color corners), we simply cut out the octahedron from the three-dimensional cube and paint the inner cut surface in purple, as a result the corners of the cube became tetrahedrons painted in 4 colors. Then we duplicated all the corners of the cube, turned the inner edge of the tetrahedra outward and painted it gray, resulting in my charm.
Of course, the main difficulty of my work was not to use Delphi to write a program depicting a four-dimensional puzzle, but to develop an algorithm for solving such a puzzle. That is, I had an idea, a mathematical representation, and OpenGL was the only means I was familiar with for depicting three-dimensional graphics.
Now we will consider what the hyperface rotation is. In the puzzle described there are only 8 hyperfaces, each of them is a cube. The rotation of the hyper face is essentially the rotation of one cube relative to another. For example, the left cube is relative to the right, or internal to external. The options to rotate the cube 24, because each of the 6 faces can be rotated by one of 4 sides. We have 8 such cubes, so in one move we have 192 invariant arrangement of the puzzle elements. I will cite a few of them below, under the spoiler.
The main assembly sequence was as follows:
1. The heuristic method, which places the elements with gray colors at the position of the outer hyper face, called Kata, respectively, all elements with purple colors after this stage will be in the inner hyper face Ana.
2. Orientation of gray colors of the outer facet outward.
3. Orientation of the purple colors of the inner hyperface inward.
4. Placement of elements of the outer hyper face according to the solution table of a three-dimensional cube 2x2x2 (of which there are only 3674160).
5. Placing the elements of the inner hyper face according to the same decision table.
On the first point, there were no special difficulties to place the gray outside, the purple inside was just a simple brute force, well, maybe slightly optimized, the whole essence of the algorithm looks like we twist this sideways, we twist the other, rearrange a couple of times, oh, that's it!
The second stage had the algorithmic complexity O (192 ^ 3), but only 256 invariants, so it was decided to create a permanent table with pre-computed combinations of solutions (essentially an analogue of OLL in the Friedrich method for the Rubik's cube). Makes a maximum of 6 moves.
The third stage, although it was decided exactly as the second, but the exponential complexity of the order O (192 ^ 4) led to two-day searches, and the number of invariants was already 65536. Makes a maximum of 8 moves.
But after orientation of colors on the Ana-Kata facets, we reduce the problem to a three-dimensional cube. The fourth stage uses a table of 3674160 invariants, the solution of a three-dimensional cube is a maximum of 11 moves. So the outside hypercube is assembled.
For the fifth stage, we use the same solutions of the three-dimensional cube, with the only exception that for each rotation of any face, the inner cube rotates with the necessary side relative to the exterior for each rotation, as a result, the outer, already assembled, facet rotates only its right-hand side and remains always almost collected.
That is, using the tables, the computer now managed the microseconds to search, but now only caching the table from the HDD to the RAM takes a few minutes when initializing the program. Well, if there are three pre-calculation tables at once, the assembly algorithm no longer seems complicated.
Therefore, first I will talk about how I imagine a four-dimensional puzzle.

Tesseract
To begin with, imagine how a three-dimensional cube is obtained. Let's take one-dimensional space: everything that we can depict in it is limited to one-dimensional objects, such as a point, a segment, a ray, a straight line. Draw a segment of unit length AB [0,1]. Now we will add the second dimension: the ordinate axis will be directed upwards, and our unit segment AB lies on the x-axis, in the Cartesian coordinate system.
')
Perhaps the two-dimensional space is most familiar to human understanding, because neither the sphere, nor the cube, will not work, we are accustomed to depict them as a projection on a plane. Well, with two-dimensional space, we have no problems, so let's think about how to get a square. So, we take the segment AB (vertices A (0,0) and B (1,0)) on the abscissa axis, retreat exactly one on the ordinate axis and duplicate the segment, let's call it CD, with points C (0,1) and D (1,1).
To get a square, we now need to connect the corresponding vertices, that is, connect the vertex A (0,0) with its duplicate C (0,1), and connect the vertex B (1,0) with D (1,1). Now we have an ACDB square. Having understood how it works in two-dimensional space, it will be quite easy to understand how a cube is made in three-dimensional. So the points:
1. Add the third dimension, the axis of applicat will be directed into depth.
2. Duplicate ACDB by retreating by one along the axis of applicate, the vertices are transformed as follows:
A (0,0,0) -> H (0,0,1)
C (0,1,0) -> F (0,1,1)
D (1,1,0) -> G (1,1,1)
B (1,0,0) -> E (1,0,1)
3. Connect the corresponding vertices of the squares.
Now the reader is mentally prepared to see the tesseract:
In fact, we duplicate the cube, shifting along the axis of the fourth dimension, and connect the corresponding vertices - you can’t think of something easier. For clarity, we will increase the duplicate cube by placing the original cube inside it. This image is most often used when trying to project a tesseract onto a plane:

To emphasize that all the segments at tesseract are single and to show equal projection, the 4-D cube can be animated:

But this is all a saying, and the tale is ahead!
From tesseract to puzzle
Now let's see what there is a four-dimensional puzzle, and most importantly how to portray it.
As is known, a cube has six faces, therefore, a three-dimensional puzzle of 6 colors. To simplify our life, we will work with a 2x2x2 cube, in particular, it will be very useful for us that the permutations of such a cube are only 3 ^ 6 * 7! = 3674160.

We list the faces:
- On the abscissa axis Left-Right, color green-blue.
- On the y-axis Down-Up, color yellow-white.
- On the axis of the front-back applique, color red-orange.
Turn on the warp drive and open the wormhole in the fourth dimension!
This is how foreign mathematicians depict a four-dimensional puzzle:

That is, in fact, we just took a three-dimensional cube 2x2x2, added an axis to the fourth dimension and got the fourth line:
- Along the axis of the fourth dimension Ana-Kata, color purple-gray.
It should be noted that now all groups of 8 colors are three-dimensional facets, and not two-dimensional faces (which had 4 colors each). Now, how to imagine exactly the same (mathematically equivalent) four-dimensional cube I:

If we take the inner part of the puzzle (that is, the cube consisting of 8 three-color corners), we simply cut out the octahedron from the three-dimensional cube and paint the inner cut surface in purple, as a result the corners of the cube became tetrahedrons painted in 4 colors. Then we duplicated all the corners of the cube, turned the inner edge of the tetrahedra outward and painted it gray, resulting in my charm.
Of course, the main difficulty of my work was not to use Delphi to write a program depicting a four-dimensional puzzle, but to develop an algorithm for solving such a puzzle. That is, I had an idea, a mathematical representation, and OpenGL was the only means I was familiar with for depicting three-dimensional graphics.
Hyperface
Now we will consider what the hyperface rotation is. In the puzzle described there are only 8 hyperfaces, each of them is a cube. The rotation of the hyper face is essentially the rotation of one cube relative to another. For example, the left cube is relative to the right, or internal to external. The options to rotate the cube 24, because each of the 6 faces can be rotated by one of 4 sides. We have 8 such cubes, so in one move we have 192 invariant arrangement of the puzzle elements. I will cite a few of them below, under the spoiler.
Faces Turns
Rotate the inner hyperline.

Rotate front facet.

Notice that this is only one turn: first, the cube is directed down with the desired face, then rotates around the vertical axis with the desired side. This is how 24 turns on each facet are formed.

Rotate the inner hyperline.

Rotate front facet.

Notice that this is only one turn: first, the cube is directed down with the desired face, then rotates around the vertical axis with the desired side. This is how 24 turns on each facet are formed.
Assembly
Mixed cube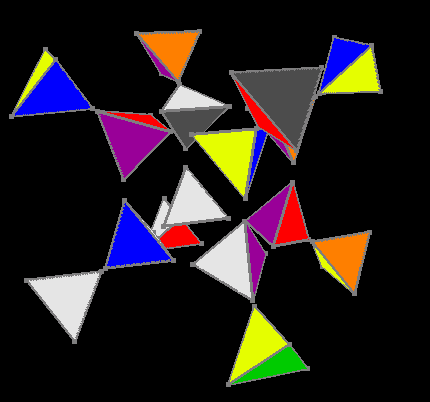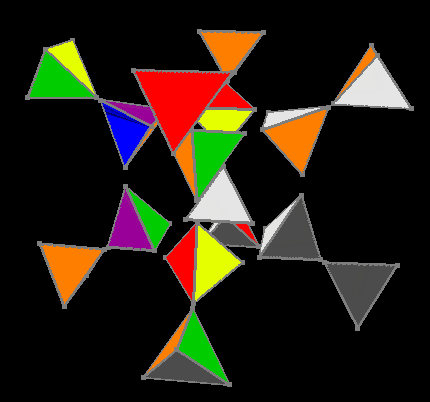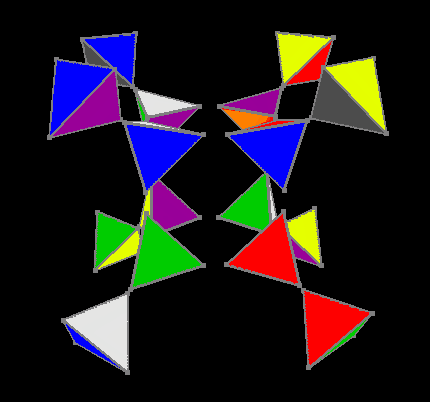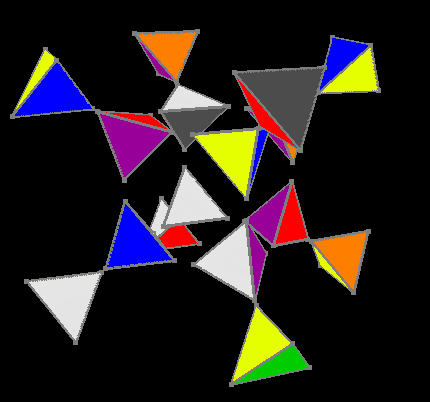
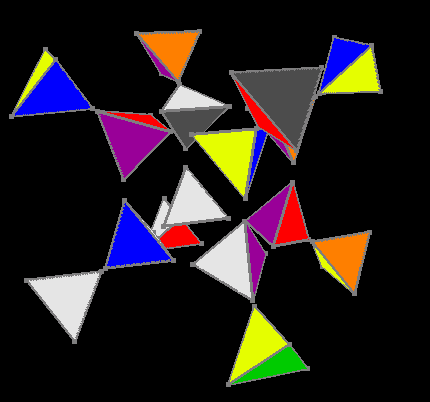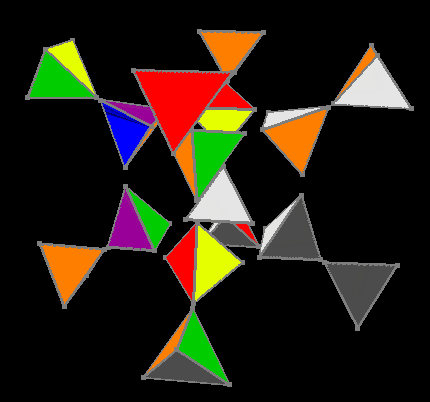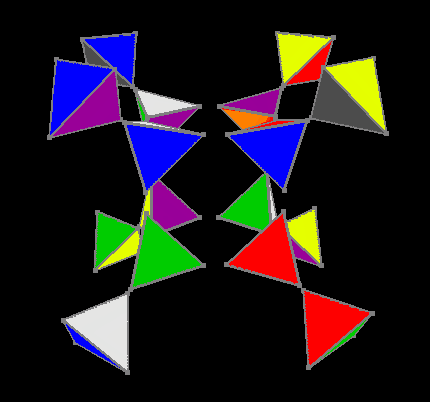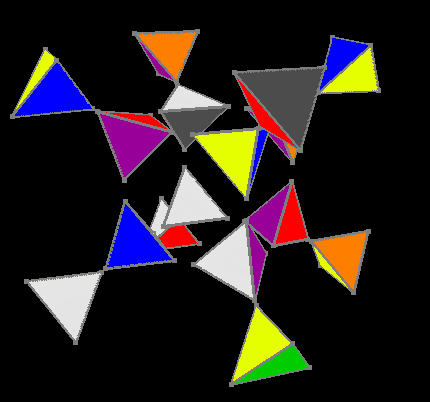
The main assembly sequence was as follows:
1. The heuristic method, which places the elements with gray colors at the position of the outer hyper face, called Kata, respectively, all elements with purple colors after this stage will be in the inner hyper face Ana.
2. Orientation of gray colors of the outer facet outward.
3. Orientation of the purple colors of the inner hyperface inward.
4. Placement of elements of the outer hyper face according to the solution table of a three-dimensional cube 2x2x2 (of which there are only 3674160).
5. Placing the elements of the inner hyper face according to the same decision table.
On the first point, there were no special difficulties to place the gray outside, the purple inside was just a simple brute force, well, maybe slightly optimized, the whole essence of the algorithm looks like we twist this sideways, we twist the other, rearrange a couple of times, oh, that's it!
The second stage had the algorithmic complexity O (192 ^ 3), but only 256 invariants, so it was decided to create a permanent table with pre-computed combinations of solutions (essentially an analogue of OLL in the Friedrich method for the Rubik's cube). Makes a maximum of 6 moves.
The third stage, although it was decided exactly as the second, but the exponential complexity of the order O (192 ^ 4) led to two-day searches, and the number of invariants was already 65536. Makes a maximum of 8 moves.
Oriented external and internal colors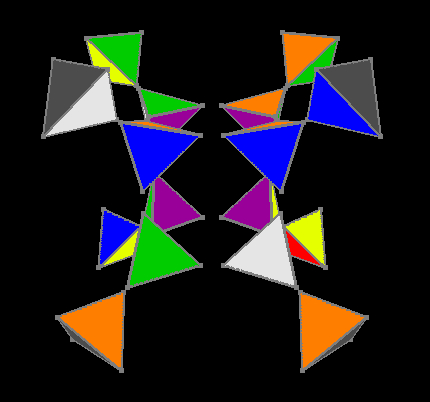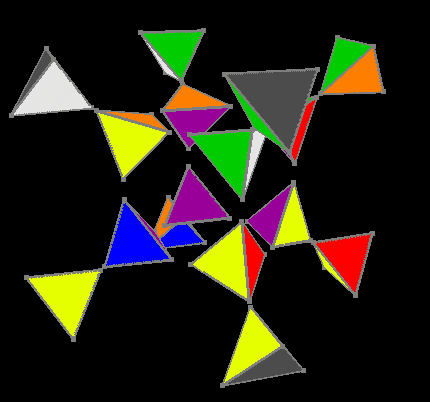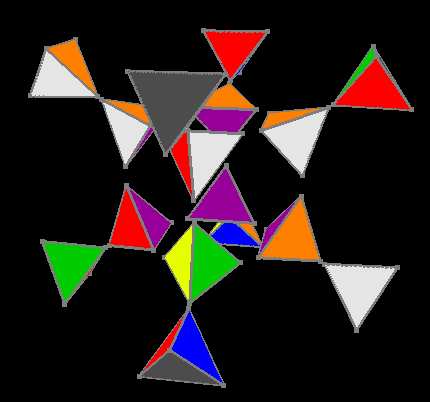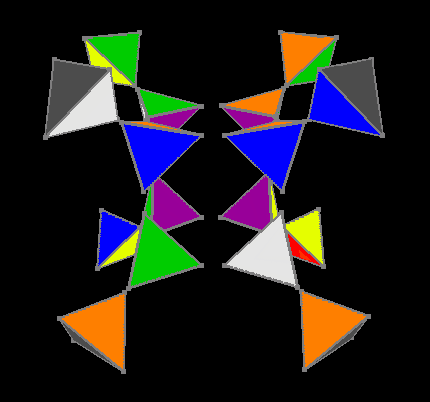
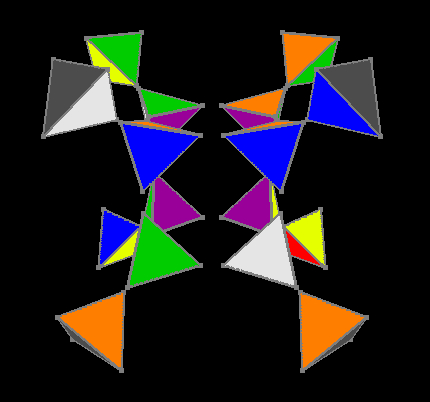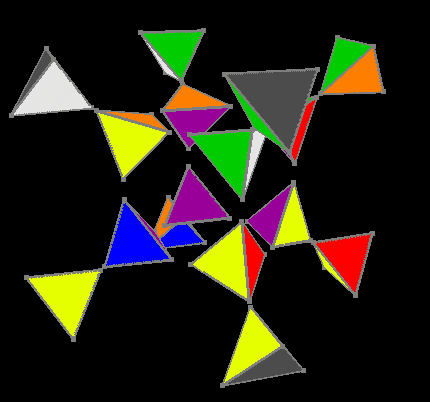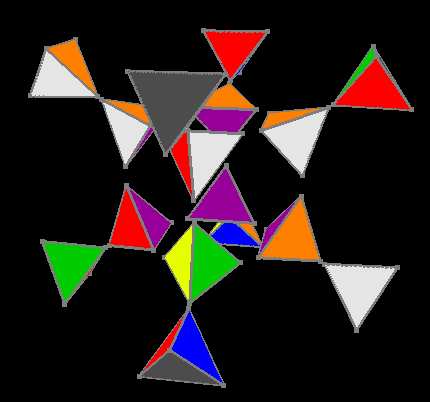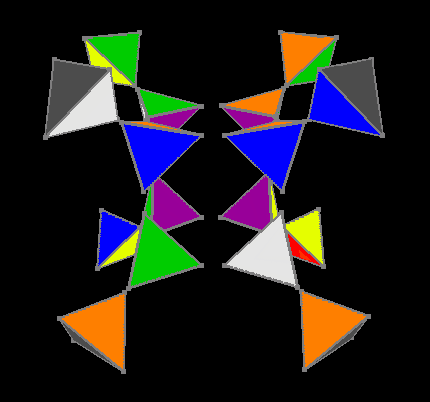
But after orientation of colors on the Ana-Kata facets, we reduce the problem to a three-dimensional cube. The fourth stage uses a table of 3674160 invariants, the solution of a three-dimensional cube is a maximum of 11 moves. So the outside hypercube is assembled.
External facet assembled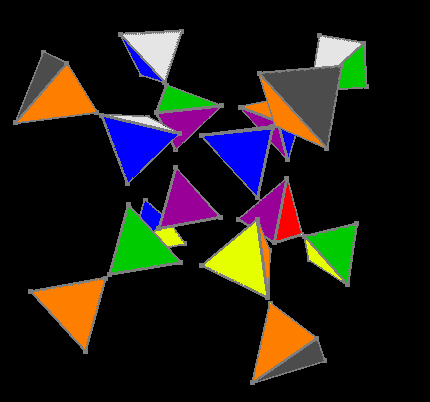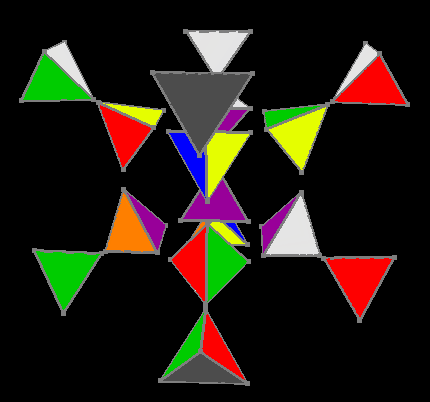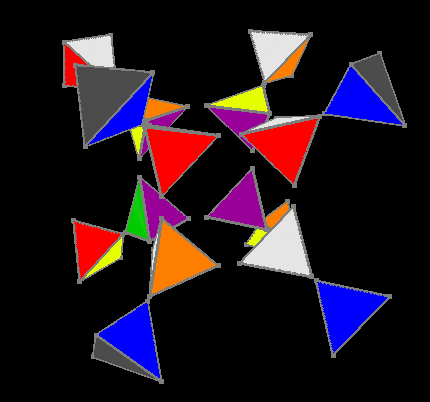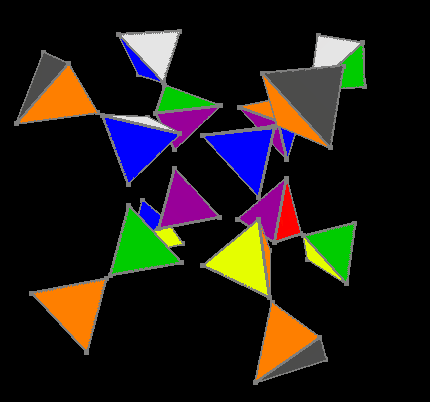
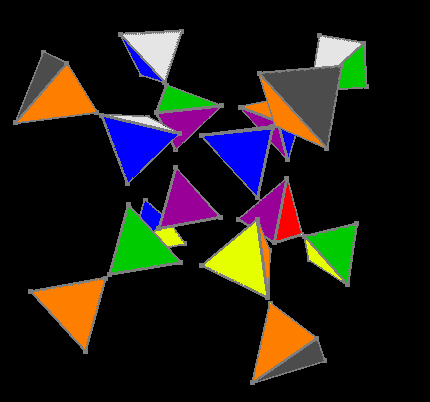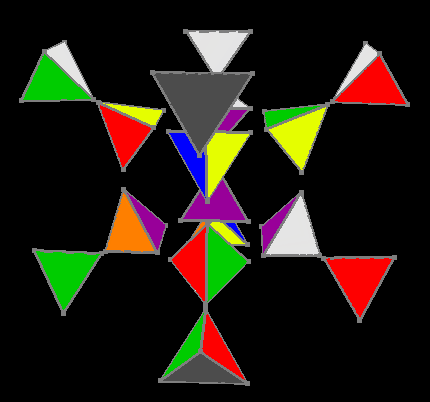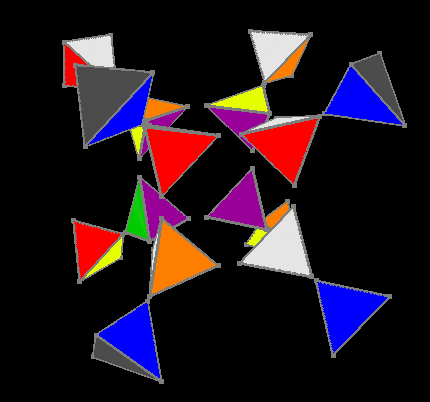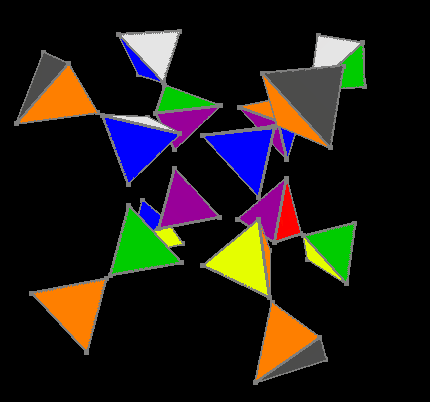
For the fifth stage, we use the same solutions of the three-dimensional cube, with the only exception that for each rotation of any face, the inner cube rotates with the necessary side relative to the exterior for each rotation, as a result, the outer, already assembled, facet rotates only its right-hand side and remains always almost collected.
Fifth stage
At the outer edge, the same right side rotates, and at the inner edge, we always turn the side to be turned.

At the outer edge, the same right side rotates, and at the inner edge, we always turn the side to be turned.
That is, using the tables, the computer now managed the microseconds to search, but now only caching the table from the HDD to the RAM takes a few minutes when initializing the program. Well, if there are three pre-calculation tables at once, the assembly algorithm no longer seems complicated.
Whole dice assembly

Source: https://habr.com/ru/post/270935/
All Articles