Online algorithms in high-frequency trading: problems of competition

High Frequency Trading [eng. High-frequency trading, HFT-trading] today has a big impact on modern financial markets. Twenty years ago, most of the trading took place on stock exchanges, for example, on the New York Stock Exchange, where people dressed in bright costumes actively gesticulated and shouted their offers to buy or sell securities. Today, trading is usually carried out using electronic servers in data centers, where computers exchange offers to buy and sell by sending messages over the network. This transition from trading in the operational building of the exchange to electronic platforms was especially beneficial for HFT companies, which invested a lot in the necessary infrastructure for trading.

In spite of the fact that the place and participants of trade externally changed a lot, the goal of traders - both electronic and ordinary - remained unchanged - to acquire an asset from one company / trader and sell it to another company / trader at a higher price. The main difference between a traditional trader and a HFT trader is that the latter can trade faster and more often, and the retention time of such a trader’s portfolio is very low. One operation of a standard HFT algorithm takes a fraction of a millisecond, which traditional traders cannot match, since a person blinks about once every 300 milliseconds. As HFT algorithms compete with each other, they face two problems:
')

• Every microsecond they process a large amount of data;
• They need to be able to react very quickly on the basis of these data, because the profit they can extract from the signals they receive decreases very quickly.

Online algorithms are a common class of algorithms that can be used in HFT trading. In such algorithms, new input variables arrive sequentially. After each new input variable is processed, the algorithm must make a specific decision, for example, whether to place a buy / sell request. This is the main difference between online algorithms and offline algorithms, in which it is assumed that all input data is available at the time of decision making. Most of the problems of practical optimization in such areas as computer science and methods of research of operations are exactly online tasks [1].

In addition to solving online problems, HFT algorithms also need to respond extremely quickly to market changes. To respond to a situation faster, an online trading algorithm must work efficiently with memory. Storing a large amount of data reduces the speed of any computer, so it is important that the algorithm uses the minimum amount of data and parameters that can be stored in high-speed memory, for example, in the first-level cache memory (L1). In addition, this set of parameters should reflect the current state of the market and be updated as new variables become available in real time. Thus, the smaller the number of parameters that need to be stored in memory, and the less calculations need to be made for each of these parameters, the faster the algorithm will be able to respond to market changes.

Given the speed requirements and the online nature of HFT trading tasks, the class of single-pass algorithms can be successfully applied in HFT trading. At each selected point in time, these input algorithms receive one data element and use it to update the set of available parameters. After the update, one of the data elements is discarded, and thus only the updated parameters are stored in memory.

When developing an HFT algorithm, three problems may arise. The first is to estimate the moving average liquidity: solving this problem can help the HFT algorithm determine the size of the order that is most likely to be successfully executed on this electronic exchange. The second is to estimate rolling volatility: solving this problem helps determine the short-term risk for a given position. The third problem is based on the concept of linear regression, which can be used in pair trading of related assets.
Each of these problems can be easily solved with the help of a single-pass online algorithm. This article describes how to back-test a single-pass algorithm based on data taken from the book of limit orders for highly liquid stock investment funds, and gives recommendations on how to regulate the operation of these algorithms.

Online algorithms in HFT trading

One of the advantages of HFT traders over other market participants is the speed of reaction. HFT companies can track any movement in the market - that is, the information contained in the book of limit orders - and on its basis make an appropriate decision within a few microseconds. Although the actions of some HFT algorithms may be based on data from a source outside the market (say, when analyzing news reports, measuring temperature, or evaluating market trends), most make decisions solely on the basis of messages received directly from the market. According to some estimates, quotes on the New York Stock Exchange are updated approximately 215,000 times per second [2]. The main task of HFT algorithms is to process the received data so that you can make the right decisions, for example, when you need to set a position or reduce risk. The examples in this article take into account that HFT algorithms can see any price updates of the best bid or ask, including data on their sizes. Such a subclass of data contained in the book of limit orders is often called information from the book of orders of the first level (Level-1).

This article details three examples of online algorithms, each of which is intended for use in HFT trading:

• Online algorithm for calculating the expectation . Designed to find a parameter based on which you can predict the available liquidity, calculated as the sum of the size of the best bid and ask, over a fixed period of time in the future. Determining this value can help estimate the size of the application, which will most likely be executed at the best price given this delay.
• Online algorithm for calculating variance . It is intended to find a parameter, on the basis of which the realized volatility can be predicted at a fixed time interval in the future. Determining this value can help assess the short-term risk of stockpiling.
• Online algorithm for calculating the regression coefficient . Designed to find a parameter based on which you can predict the expected profit from holding the long and short positions of a pair of related assets. Determining this value can help in creating a signal that is supplied in the case when a long and short position is most likely to be profitable.

In each of the three cases, the algorithm contains a single parameter, "alpha", that regulates the speed with which unnecessary information is discarded. In Figure 1, blue indicates the approximate change in liquidity (the sum of the bid and ask values). Red and green are the changes in the liquidity parameter with the values ​​of the parameter “alpha” equal to 0.9 and 0.99, respectively. Please note that as the alpha approaches unity, the signal level becomes more uniform and more accurately reflects the trend in the source data.



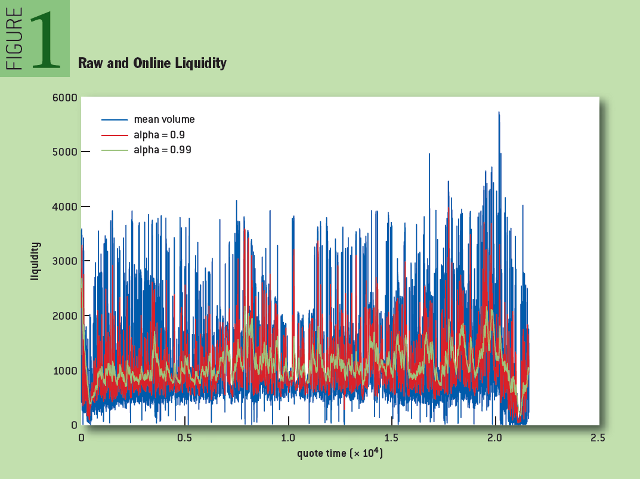
Fig. 1: Crude and online liquidity

Figure 2 shows the change in volatility for different values ​​of the alpha parameter in real time. Note that, as in the previous case, as the alpha increases, the graph curve becomes smoother. A higher alpha value gives a more even signal, but a high load of past data causes a lag from the current trend. As will be shown later, the choice of a suitable alpha value will either give a more even signal, or reduce the lag from the trend.



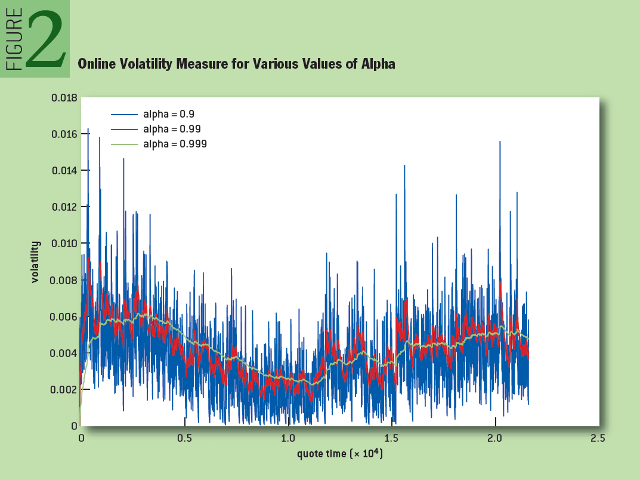
Fig. 2: Online volatility measurement for different alpha values

To show how the online regression algorithm works, we looked at time series composed of average prices for SPY and SSO shares — two related exchange-traded investment funds (SSO — the same SPY, but the amount of its borrowed funds is twice as large). As shown in Figure 3, the relationship between these two assets in the process of their change during the day is close to linear. Figure 4 shows the change in the expectation and the free term for two values ​​of "alpha".



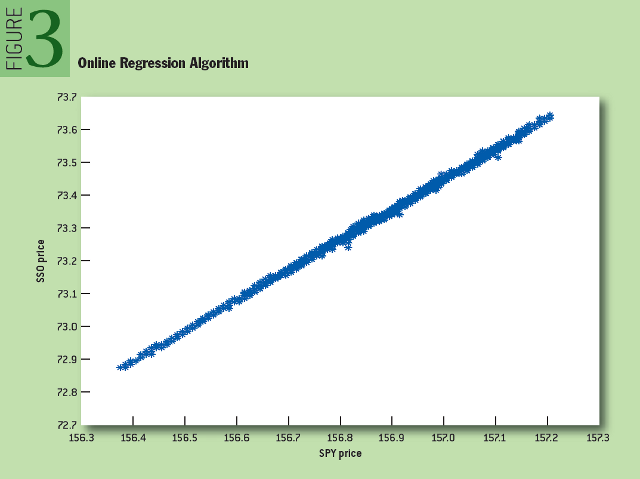
Fig. 3: Online Regression Algorithm



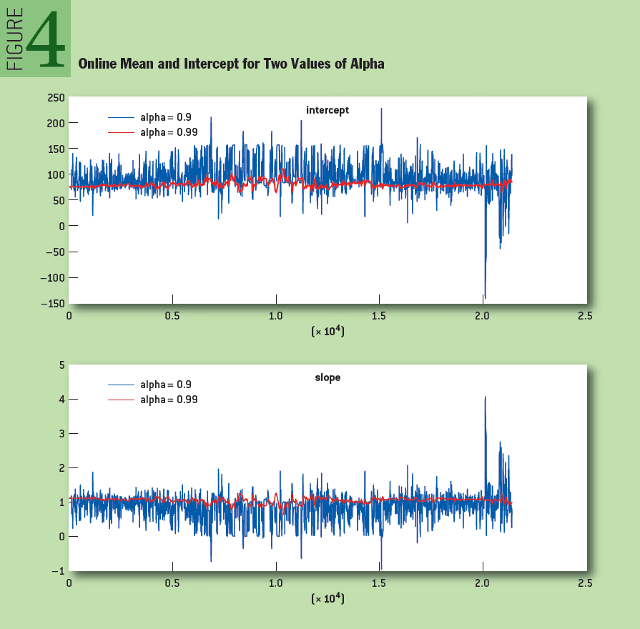
Fig. 4: Change in expectation and idle for two alpha values

Single Pass Algorithms

As the name implies, the single-pass algorithm reads an input variable exactly once and then discards it. This type of algorithm effectively allocates memory, as it saves the minimum amount of data. This section provides three important examples of single-pass algorithms: an exponentially moving average, an exponentially weighted variance, and an exponentially weighted regression. The next section will discuss the use of these algorithms in HFT trading.

To begin with, let's briefly review the concept of a simple moving average for a given time series. It is an estimate of the mathematical expectation for a time series with a “sliding” window of constant size. In the financial sphere, this estimate is often used to determine the price trend, in particular, when comparing two values ​​of a simple moving average - in the case of a “long” window and in the case of a “short” window. As an application, you can also consider a situation where the average trade volume over the past five minutes helps to predict the trade volume in the next minute. In contrast to the exponential moving average, a simple moving average cannot be determined using a single-pass algorithm.

Let (X _t ) _t = X ₀ , X ₁ , X ₂ , ... be the sequence of received input variables.

For each individual point in time t, we need to predict the value of the next variable X _{t + 1} . For M> 0 and t ≥ M, a simple moving average with a window of size M is defined as the mathematical expectation of the last M observations for the time series (X _t ) _t , i.e. 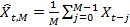. The moving average can also be calculated using the following recursion:

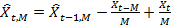. (one)

Although it is an online algorithm, however, it is not one-pass, because it has to process each input element twice: when it should be taken into account when calculating the moving average and when it should be excluded from the estimate. Such an algorithm is called a two-pass algorithm and requires storage in memory of an entire array of size M.

Example 1: Single-pass algorithm of exponentially weighted average

Unlike the average 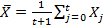The exponentially weighted average determines the exponentially decreasing values ​​of the weighting factors of previous observations: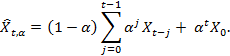



Here α is a weighted parameter that is chosen by the user and must satisfy the condition 0 <α ≤ 1. Due to the fact that the most recent input parameters play an important role for an exponentially weighted average, compared to earlier data elements, it is often considered to be quite accurate approximation of a simple moving average.

Unlike a simple moving average, the exponentially weighted average takes into account all previous data, not just the latest M observations. Moreover, if we continue to compare simple moving average and exponentially weighted average, in Figure 5 you can see how many data elements 80%, 90%, 95%, 99% and 99.9% of the weight function depends on α are obtained during the assessment. For example, if α = 0.95, then the last M = 90 received data elements constitute 99% of the estimated value. It should be noted that if the time series of (Xt) t is very “heavy tails”, then the exponentially smoothed average may consist mainly of extreme observations, while the moving average less often depends on extreme observations, since they are ultimately excluded from the observation window. Frequent repetition of the evaluation procedure can solve the problem of long-term data storage in memory with exponential smoothing.



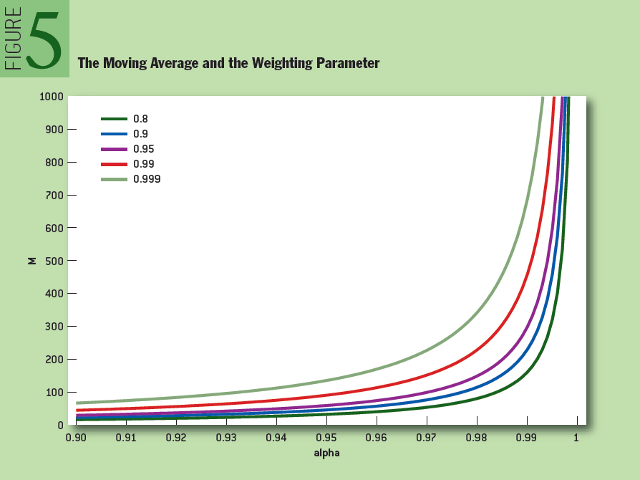
Fig. 5: Moving average and weight parameter

The reason for choosing an exponentially moving average instead of a simple moving average for use in the HFT algorithm is that it can be determined using the single-pass algorithm first mentioned in the work of R.G. Brown (1956) [3].

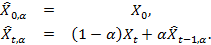. (2)

This formula also indicates that using the parameter α you can adjust the weights of the last observations by comparing them with the previous ones.

Example 2: One-pass algorithm of exponentially weighted variance

The exponential smoothing described in the previous section allows us to estimate the moving average for time series. In finance, the volatility of time series often plays an important role. In other words, volatility should reflect the frequency of fluctuations of time series relative to their average level. In the financial theory of HFT trading there is no unique definition of volatility. In this section, the volatility is treated as the standard deviation (square root of the variance) of the data element for time series (X _t ) _t . As in the case of the exponentially weighted moving average from the previous section, you can develop a single-pass online algorithm that will estimate the volatility for time series based on a scheme of exponentially weighted coefficients.

The variance of a random variable is determined by the formula Var (X) = E [X - E [X]) ² ]. In order to estimate the exponentially weighted variance of time series, it is necessary first to estimate two parameters - the expectation E [X] and the variance:



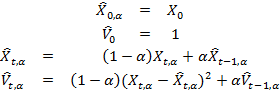
The standard deviation of each subsequent control point X _{t + 1} is estimated as 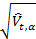. In this example, the input parameter α ∈ (0,1) is also selected by the user and determines the values ​​of the weights of the past data, which are compared with the last of the received input data. In this case, we take the initial value of the statistical estimate to be 1 - it [estimate], generally speaking, can take any value. Another way is to enter a trial period during which the time series is monitored and, as an initial estimate, use the standard deviation estimate for time series in this “test” window. Of course, a similar method can also be used in determining the evaluation of an exponentially weighted average.

Example 3: Single-pass exponentially weighted linear regression algorithm

The latest example is a single-pass online algorithm based on an exponentially weighted linear regression model. This model is similar to the model of ordinary linear regression, but unlike it, it focuses more attention (in accordance with exponential weighting) on ​​recent observations than on earlier ones. As already shown, such regression methods play an important role in HFT strategies and help determine the relationship between different assets, in particular, they can be used in pair trading strategies.

In our model, we consider two-dimensional time series (X _t , Y _t ) _t and assume that the variables X and Y are related by a linear relationship, which also includes the random error ε _t with zero expectation, that is:

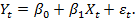. (3)

The variable Y is called the response variable, and the variable X is the explanatory variable. For simplicity, we assume that we have one explanatory variable, although a generalization to several explanatory variables is not so difficult to make. With the standard approach to the definition of linear regression using an offline algorithm, the parameters β ₀ and β _{1 are} selected after all the observations. The data elements of each individual observation are recorded in a separate vector Y = (Y ₀ , Y ₁ , ..., Y _t ) ^T or matrix



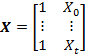
A column of units in the matrix X corresponds to the free term in equation 3. If we write the parameters β ₀ and β ₁ as the vector β = (β ₀ , β ₁ ) ^T , then the ratio between Y and X can be compactly written in the matrix form:

Y = Xβ + ε

where ε is the vector of stochastic errors, each of which has zero expectation.

The most common approach to estimating the parameter β is to use the standard method of least squares, that is, β is chosen so that the sum of the squares of the remainder terms 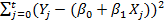was minimal. The solution to this minimization problem will be .

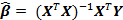As in the estimation of the expectation and variance, later observations should play an important role in the estimation of the parameter β. In addition, a single-pass algorithm for finding β values ​​is necessary for performing calculations.

Next, consider a recursive method that sequentially updates the values ​​of the vector β and minimizes the expression:



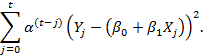
Recall that the parameter must be in the interval (0,1) and selected by the user. The β _{0 and} β ₁ parameters using the weighted least squares method can be calculated using an efficient one-pass online algorithm. At each step of the algorithm, the matrix M _{t of} dimension 2 × 2 and the vector V _{t of} dimension 2 × 1 must be stored in memory and updated as new data is received in accordance with the following recursive expressions:



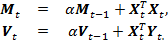
As for the estimation of the expectation and variance, for them the initialization of recursion variables can be carried out in a trial period. As a result, by the time t, the best estimate of β will be calculated by the formula 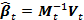. In the literature, this method is called the recursive least squares method with exponential forgetting [2].

Alpha score

How to determine the optimal value of "alpha", the only parameter used in each of the above models of online algorithms? Our approach in each of the three models was to determine the response function, the value of which we want to predict, and to minimize the square of the difference between the response ri and our parameter f _i :



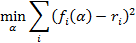
This method allows you to determine the optimal value of "alpha" on the basis of historical time series. Another approach is to estimate the optimal value of "alpha", which is also carried out in real time. However, it requires more work and is beyond the scope of this article.

Now let's take a closer look at the described estimates of online algorithms and estimate the optimal value of “alpha” on a particular data set.
1. The estimate of the average liquidity is calculated by the formula:



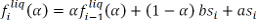
where the index i denotes the point in time when the quote was set. The response function is defined as liquidity, which is observed after ten seconds:



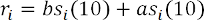
where the term b _si (10) is the bid size ten seconds after setting the i-th quotation. After the optimization with the alpha parameter, it was shown that the optimal alpha value for our data is 0.97. It is presented in Figure 6 as a scatterplot for the desired parameter and response function:



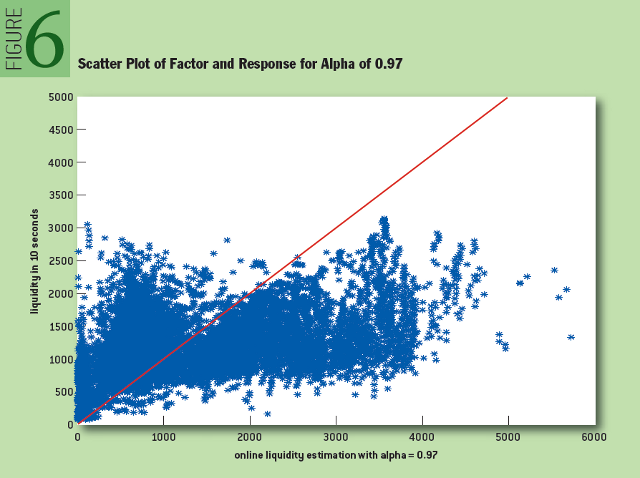
Fig. 6: The scatterplot for the desired parameter and the response function for the value of "alpha" 0.97

2. The estimation of volatility is determined by the formulas:







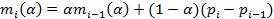
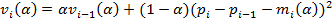
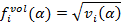
where the index i denotes the current time in seconds. The magnitude of the response is defined as the realized volatility for the last minute:



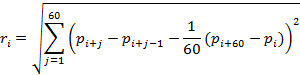
As in the previous case, as a result of sorting the values ​​of the alpha parameter, the optimal value for our data set turned out to be 0.985. Figure 7 shows the scatterplot for the desired parameter and response function:



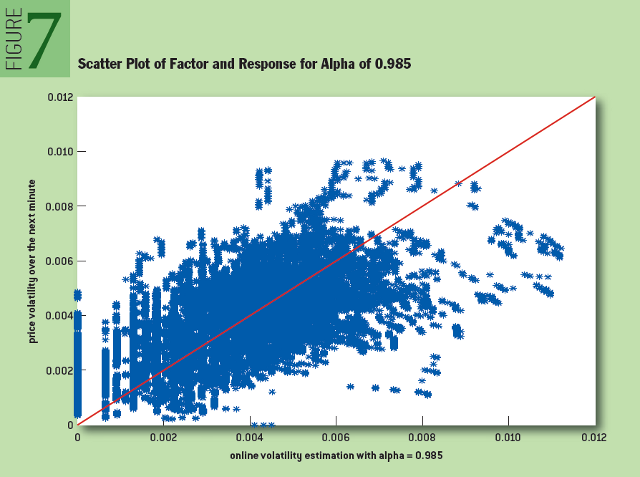
Fig. 7: Scatterplot and Response Function for Alpha 0.985

3. The regression estimate for pair trading is found by the formulas:









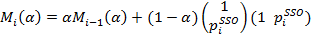
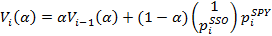
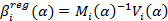
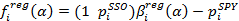
where the index i denotes the point in time when the quote was set. Parameter 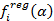denotes the value of SPY stocks compared to SSO stocks, that is, if their difference is positive, then SPY stocks are relatively cheaper, and holding a long position on SPY is likely to be profitable.

The response function is defined as the profit received in the last minute from the transaction, which consists of holding a long position per SPY share and a short position on β SSO shares:



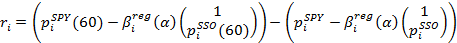
Where 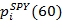represents the value of the SPY stock 60 seconds after setting the value 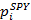. The response r _i indicates the profitability of the following strategy for holding a long and short position: “Buy one share of SPY and sell β shares of SSO at time i, close the position after 60 seconds”.

The alpha value of 0.996 turned out to be optimal on the studied data set. Figure 8 shows the scatterplot for the desired parameter and response function:



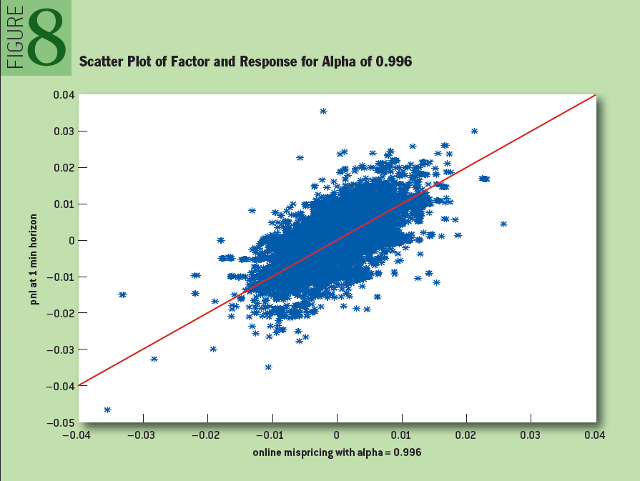
Fig. 8: Scatter diagram and response function for alpha 0.996

Conclusion

Single-pass online algorithms are an effective tool in HFT trading, where every microsecond they have to process large amounts of data and make decisions based on them very quickly. In this article, three problems faced by HFT algorithms were considered: the estimation of the moving average liquidity needed to determine the size of the order that is most likely to be executed successfully on a specific electronic exchange; estimation of volatility required to calculate the short-term risk of a transaction; sliding linear regression, which can be used in pair trade related assets. Single-pass online algorithms can play a key role in solving these problems.

Another important factor for HFT merchants, which we often write about in a blog on Habré, is the speed of work. One of the frequently used technologies to increase the speed of data acquisition and processing is direct access to the exchange , which is organized using various financial information transfer protocols. We considered the technology of direct access in this article , and wrote about data transfer protocols here ( one , two , three ).

Notes:

1. Albres S. 2003. Online Algorithms: Analysis. Mathematical programming 97 (1-2): 3-26.
2. Clark K. 2011. Improving the speed and transparency of market data. Exchange. whatheheckaboom.wordpress.com/2013/10/20/acm-articles-on-hft-technology-and-algorithms , www.utpplan.com .
3. Brown, R. G. 1956. Exponential smoothing for demand forecasting. Arthur D. Little Inc., p. 15.
4. Astrom A., Wittenmark B. 1994. Adaptive management, second edition. Addison Wesley.

About the authors:

Jacob Loveless is the executive director of Lucera and former head of high-frequency trading at Cantor Fitzgerald. Over the past ten years, Mr. Loveless managed to try himself in electronic commerce with virtually every asset in various HFT companies and on various exchanges. Prior to his career in the financial field, Mr. Lavless was in the position of a special contractor for the US Department of Defense, where he specialized in heuristic analysis of secret data. Prior to that, he was also the Chief Technical Officer (CTO) and founder of Data Scientific. The founder of the analysis of distributed systems.

Sasha Stoikov is a senior researcher at Cornell Financial Engineering Manhattan (CFEM) and a former vice president of high frequency trading at Cantor Fitzgerald. He worked as a consultant to the Galleon Group and Morgan Stanley, and also lectured at the Institute. Courant at New York University and at the Department of Production Management and Operations Research at Columbia University. He received a Ph.D. at the University of Texas and a bachelor's degree from the Massachusetts Institute of Technology.

Rolf Waeber is a quantitative analyst at Lucera, and in the past he was engaged in quantitative research in the high-frequency trading department of Cantor Fitzgerald. He participated in liquidity risk management research as part of the development of Basel II / III documents at the German Federal Bank. In 2013, Rolf received a Ph.D. degree in Operations Research and Information Engineering from Cornell University. In addition, he received bachelor's and master's degrees in mathematics from the higher technical school in Zurich, Switzerland.