I2P: Signature and EdDSA Signature Verification
In the previous article , the implementation of the Ed25519 curve itself, the addition and multiplication operations by number, the restoration of the second coordinate was considered. This article discusses how to effectively use these operations to digitally sign messages and work in I2P.
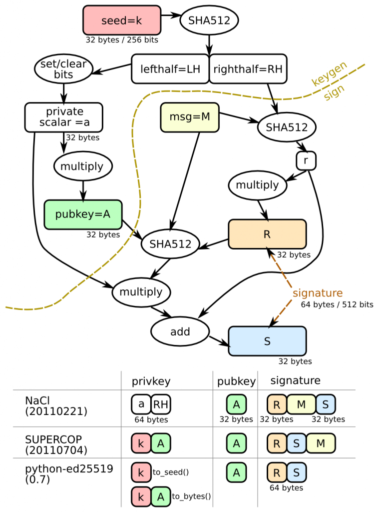
Unlike RSA, where the secret and public key can be used directly, here you have to use a more complex scheme and enter some additional object. EdDSA conceptually implements the DSA algorithm, extending it to the case of curves. The signature is a pair of numbers (R, S), for EdDSA, each is 32 bytes in length, total signature length is 64 bytes. It is not the data itself that is signed, but the hash of them. SHA512 is used as a hash function. Further, in small letters, numbers will be designated, and in capital letters - the corresponding point on the curve, obtained by multiplying the number by the base point B.
Let h be the hash of the message being signed, a the secret key, and A the corresponding public key (A = a * B). Take a random number r, and calculate R = r * B and s = r + h * a. The pair (R, s) will be the signature where R is represented by its y coordinate.
When verifying the signature, the recipient knows A and h, and it is necessary to verify the truth (R, s). For this, the equality is checked: s * B = R + h * A.
Indeed (r + h * a) * B = r * B + h * a * B = R + h * A.
Note that s is calculated directly on the basis of the secret key, and not the point generated by it, because errors in the implementation can lead to its immediate compromise. In particular, the bad choice r. To avoid this, Bernstein suggests calculating r as a hash from half of the secret key hash combined with the data being signed, but choosing r in some other way will not break the algorithm, that is, the signature values themselves will be different, but the result will be the same. We will calculate r, as suggested by Bernstein and how it is done in the official I2P.
For further calculations, we will need the previously unused curve parameter l =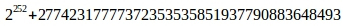
such that l * b = 0.
From this equality immediately follows that the values of the multiplier in front of the point should not exceed l, otherwise it will only lead to an increase in the amount of calculations. If the multiplier exceeds l, then it should be taken modulo, in particular the value of h, which is a SHA512 hash of 64 bytes in length.
From this, in turn, it follows that the multiplier in the multiplication operation does not exceed 32 bytes and the most significant bit is always zero.
As you can see from the formulas, one multiplication per base point is required for the signature, and two for verification of the signature: one for the base point and the second for the public key.
For a base point, it makes sense to calculate the result of multiplying by different factors in advance. The simplest is a series (B, 2 * B, 4 * B, 8 * B, ...) of only 255 points, which allows eliminating the doubling operation at each step. You can go further and expand the factor not in powers of two, but in powers of 16 and for each 4 bits of the multiplier add to the result a calculated point from the array. For this you need to calculate and store 32 * 2 * 16 points, but this is done once during the whole work. Thus, multiplication by B reduces to exactly 64 additions and the message is signed quickly. Here is how it looks in code.
Here Bi16 is an array of 64x16 pixels, and e is a 32-byte multiplier in Little Endian. Instead of the degrees 16, you can use the decomposition in powers of 256, this will lead to some acceleration, at the same time you will need to store 32 * 256 points.
To verify the signature, you will also need to multiply the public key, although it is the result of multiplying B, the factor is unknown to us, since this is the secret key. If you apply this method, you will have to keep such an array for each of them, and in I2P there are a lot of public keys - for each node from netdb its own, which are of the order of several thousand, which would lead to unnecessary memory consumption. Therefore, in order to achieve a work speed comparable to other elliptic curves, it will be necessary to improve the operation of addition.
')
As noted in the previous article , the slowest operation is division with each addition, which can be eliminated by going to homogeneous coordinates. The implementation becomes less visual, but all the implementations of elliptical cryptography are arranged there. Instead of the two coordinates of the point (x, y), a third coordinate is entered that stores the common denominator, and instead of x and y their numerators are stored, that is, from the homogeneous coordinates (X, Y, Z), the true coordinates are obtained as (X / Z, Y / Z ). In addition, the fourth coordinate T = X * Y / Z is introduced. The coordinates of the result of the addition are calculated by the following formulas:
X = (X1 * Y2 + Y1 * X2) * (Z1 * Z2-d * T1 * T2)
Y = (Y1 * Y2 + X1 * X2) * (Z1 * Z2 + d * T1 * T2)
Z = (Z1 * Z2-d * T1 * T2) * (Z1 * Z2 + d * T1 * T2)
T = (Y1 * Y2 + X1 * X2) * (X1 * Y2 + Y1 * X2)
As can be seen, the laborious operation of exponentiation in the process of addition and multiplication no longer applies.
Another disadvantage of homogeneous coordinates is the complexity of comparing two points: the X and Y coordinates cannot be directly compared - they need to be brought to a common denominator in one way or another, which requires additional calculations. To verify the signature is required to compare the points.
Rewrite the expression to verify the signature s * B = R + h * A in the form R = s * Bh * A.
Then, instead of restoring the X coordinate of the point along the Y coordinate from the signature, you can take the Y coordinate from (s * Bh * A), thereby saving another exponentiation and comparing numbers instead of points. This method requires a subtraction operation, which is implemented through additions and unary minus, defined as (-X, Y, Z, -T). Thus, the subtraction operation is performed at the same speed as the addition, and can be used to decompose in powers with negative coefficients, which allows to reduce the memory size by 2 times.
The length of the I2P address from EdDSA is 391 bytes, the signature type code is 7, denoted in the documentation as EdDSA_SHA512_Ed25519.
The length of the secret and public keys is 32 bytes, the length of the signature is 64 bytes, the first 32 bytes are R in the form of the y coordinate, the second 32 bytes are s.
All numbers are transferred to Little Endian.
Currently EdDSA is the recommended signature type for RouterInfo.
Thus, in two articles, a complete and transparent implementation of EdDSA over a library for working with large numbers from the openssl library, operating at high speed and practically used in i2pd, is described .
EdDSA Signature Algorithm
Unlike RSA, where the secret and public key can be used directly, here you have to use a more complex scheme and enter some additional object. EdDSA conceptually implements the DSA algorithm, extending it to the case of curves. The signature is a pair of numbers (R, S), for EdDSA, each is 32 bytes in length, total signature length is 64 bytes. It is not the data itself that is signed, but the hash of them. SHA512 is used as a hash function. Further, in small letters, numbers will be designated, and in capital letters - the corresponding point on the curve, obtained by multiplying the number by the base point B.
Let h be the hash of the message being signed, a the secret key, and A the corresponding public key (A = a * B). Take a random number r, and calculate R = r * B and s = r + h * a. The pair (R, s) will be the signature where R is represented by its y coordinate.
When verifying the signature, the recipient knows A and h, and it is necessary to verify the truth (R, s). For this, the equality is checked: s * B = R + h * A.
Indeed (r + h * a) * B = r * B + h * a * B = R + h * A.
Note that s is calculated directly on the basis of the secret key, and not the point generated by it, because errors in the implementation can lead to its immediate compromise. In particular, the bad choice r. To avoid this, Bernstein suggests calculating r as a hash from half of the secret key hash combined with the data being signed, but choosing r in some other way will not break the algorithm, that is, the signature values themselves will be different, but the result will be the same. We will calculate r, as suggested by Bernstein and how it is done in the official I2P.
Effective multiplication implementation
For further calculations, we will need the previously unused curve parameter l =
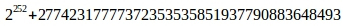such that l * b = 0.
From this equality immediately follows that the values of the multiplier in front of the point should not exceed l, otherwise it will only lead to an increase in the amount of calculations. If the multiplier exceeds l, then it should be taken modulo, in particular the value of h, which is a SHA512 hash of 64 bytes in length.
From this, in turn, it follows that the multiplier in the multiplication operation does not exceed 32 bytes and the most significant bit is always zero.
As you can see from the formulas, one multiplication per base point is required for the signature, and two for verification of the signature: one for the base point and the second for the public key.
For a base point, it makes sense to calculate the result of multiplying by different factors in advance. The simplest is a series (B, 2 * B, 4 * B, 8 * B, ...) of only 255 points, which allows eliminating the doubling operation at each step. You can go further and expand the factor not in powers of two, but in powers of 16 and for each 4 bits of the multiplier add to the result a calculated point from the array. For this you need to calculate and store 32 * 2 * 16 points, but this is done once during the whole work. Thus, multiplication by B reduces to exactly 64 additions and the message is signed quickly. Here is how it looks in code.
EDDSAPoint res {zero, one}; for (int i = 0; i < 32; i++) { uint8_t x = e[i] & 0x0F; // 4 low bits if (x > 0) res = Sum (res, Bi16[i*2][x-1], ctx); x = e[i] >> 4; // 4 high bits if (x > 0) res = Sum (res, Bi16[i*2+1][x-1], ctx); } Here Bi16 is an array of 64x16 pixels, and e is a 32-byte multiplier in Little Endian. Instead of the degrees 16, you can use the decomposition in powers of 256, this will lead to some acceleration, at the same time you will need to store 32 * 256 points.
To verify the signature, you will also need to multiply the public key, although it is the result of multiplying B, the factor is unknown to us, since this is the secret key. If you apply this method, you will have to keep such an array for each of them, and in I2P there are a lot of public keys - for each node from netdb its own, which are of the order of several thousand, which would lead to unnecessary memory consumption. Therefore, in order to achieve a work speed comparable to other elliptic curves, it will be necessary to improve the operation of addition.
')
Addition in homogeneous coordinates
As noted in the previous article , the slowest operation is division with each addition, which can be eliminated by going to homogeneous coordinates. The implementation becomes less visual, but all the implementations of elliptical cryptography are arranged there. Instead of the two coordinates of the point (x, y), a third coordinate is entered that stores the common denominator, and instead of x and y their numerators are stored, that is, from the homogeneous coordinates (X, Y, Z), the true coordinates are obtained as (X / Z, Y / Z ). In addition, the fourth coordinate T = X * Y / Z is introduced. The coordinates of the result of the addition are calculated by the following formulas:
X = (X1 * Y2 + Y1 * X2) * (Z1 * Z2-d * T1 * T2)
Y = (Y1 * Y2 + X1 * X2) * (Z1 * Z2 + d * T1 * T2)
Z = (Z1 * Z2-d * T1 * T2) * (Z1 * Z2 + d * T1 * T2)
T = (Y1 * Y2 + X1 * X2) * (X1 * Y2 + Y1 * X2)
As can be seen, the laborious operation of exponentiation in the process of addition and multiplication no longer applies.
Another disadvantage of homogeneous coordinates is the complexity of comparing two points: the X and Y coordinates cannot be directly compared - they need to be brought to a common denominator in one way or another, which requires additional calculations. To verify the signature is required to compare the points.
Subtract two curve points
Rewrite the expression to verify the signature s * B = R + h * A in the form R = s * Bh * A.
Then, instead of restoring the X coordinate of the point along the Y coordinate from the signature, you can take the Y coordinate from (s * Bh * A), thereby saving another exponentiation and comparing numbers instead of points. This method requires a subtraction operation, which is implemented through additions and unary minus, defined as (-X, Y, Z, -T). Thus, the subtraction operation is performed at the same speed as the addition, and can be used to decompose in powers with negative coefficients, which allows to reduce the memory size by 2 times.
I2P Addresses with EdDSA
The length of the I2P address from EdDSA is 391 bytes, the signature type code is 7, denoted in the documentation as EdDSA_SHA512_Ed25519.
The length of the secret and public keys is 32 bytes, the length of the signature is 64 bytes, the first 32 bytes are R in the form of the y coordinate, the second 32 bytes are s.
All numbers are transferred to Little Endian.
Currently EdDSA is the recommended signature type for RouterInfo.
Thus, in two articles, a complete and transparent implementation of EdDSA over a library for working with large numbers from the openssl library, operating at high speed and practically used in i2pd, is described .
Source: https://habr.com/ru/post/270753/
All Articles