Regular expression searches can be quick and easy.
In this article, we will look at two ways to search using regular expressions. One is widely distributed and used in standard interpreters of many languages. The second is used in few places, mainly in awk and grep implementations. Both approaches vary greatly in their performance:
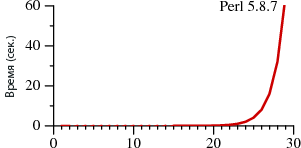
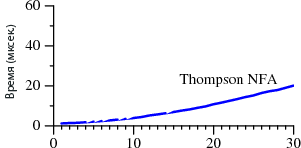
In the first case, the search takes A? n A n of time, in the second - A n .
')
The degrees denote the repeatability of rows, that is, A? 3 A 3 is the same as A? A? A? AAA. Charts reflect the time required to search through regular expressions.
Note that in Perl it takes more than 60 seconds to search for a string of 29 characters. And with the second method - 20 microseconds . It's not a mistake. When searching for the 29-character string, Thompson NFA runs about a million times faster. If you need to find a 100-character string, Thompson NFA can handle in less than 200 microseconds, and Perl will need more than 10 to 15 years. Moreover, it is taken only as an example, in many other languages the same picture is observed - in Python, PHP, Ruby, etc. Below we consider this question in more detail.
Surely you find it hard to believe the given data. If you’ve worked with Perl, you’d hardly notice its poor performance when working with regular expressions. The fact is that in most cases, Perl handles them fairly quickly. However, as follows from the graph, you can encounter the so-called pathological regular expressions, on which Perl begins to slip. At the same time, Thompson NFA has no such problem.
A logical question arises: why not use the Thompson NFA method in Perl? This is possible and should be done, and this will be discussed further.
Previously, regular expressions were a vivid illustration of how the use of the “good theory” can lead to the creation of good programs. Originally, they were created as a simple theoretical computational model, and then Ken Thompson implemented them in one of the versions of the QED text editor for CTSS. Dennis Ritchie did the same in his own version of QED for GE-TSS. Later, Thompson and Ritchie had a hand in creating UNIX, moving regular expressions there as well. In the late 1970s, they were one of the main features of this OS and were used in tools such as ed, sed, grep, egrep, awk and lex.
Today, regular expressions provide a no less vivid illustration of how ignoring the “good theory” leads to the creation of bad programs. Implementations of regular expressions in many modern tools work much slower than those used 30 years ago in UNIX tools.
In this article, we will look at various aspects of the “good theory”, as well as its practical implementation of the Thompson algorithm. It consists of less than 400 lines of C and is very close to that used in Perl, Python, PCRE and a number of other languages.
This is the name used to describe string data patterns. If a certain set of string data is similar to that described by a regular expression (RV), then we are talking about the coincidence of the RV with this string data.
The simplest case of a regular expression is a single letter character. With the exception of metacharacters - *, +,?, (,), And |, - all characters are equal to themselves. To search for matches with metacharacters, you need to add a backslash: the combination of characters \ + is similar to +.
Two regular expressions can be transformed or combined, creating a new regular expression: if E 1 matches S, and E 2 matches t, then E 1 | E 2 matches S or T, and E 1 E 2 corresponds to ST.
Metacharacters *, + and? are loop operators:
Operators are prioritized by increasing the degree of binding (binding): first, alternation, then concatenation, and, finally, repetition operators. Parentheses can be used to distinguish subexpressions, like arithmetic ones: AB | cd corresponds to (AB) | (cd), AB * corresponds to A (B *).
The syntax described is a subset of the syntax used in egrep. This is enough to describe all regular languages (regular languages). Roughly speaking, a regular language is a set of lines that can be found in the text in one pass using a fixed amount of memory. Modern implementations of regular expressions (in Perl and several other languages) use numerous new operators and control sequences . This makes PB more concise, and sometimes quite incomprehensible. But efficiency is not added, since almost all of these new expressions can be expressed using the “traditional” syntax, just in a longer form.
Additional features provide so-called feedbacks (backreferences). The back reference \ 1 or \ 2 corresponds to a line similar to the previous expression enclosed in parentheses. (cat | dog) \ 1 matches catcat and dogdog, not catdog or dogcat.
From the point of view of the theory, regular expressions with feedback are no longer regular expressions. The use of backlinks has its considerable price: in different implementations it is necessary to use exponential search algorithms. Of course, Perl (like other languages) cannot be relieved of feedback support. But in their absence, you can use much faster algorithms.
State machines can be used to describe patterns. They are also known as state machines. In this article, the concepts of "automatic" and "machine" will be interchangeable.
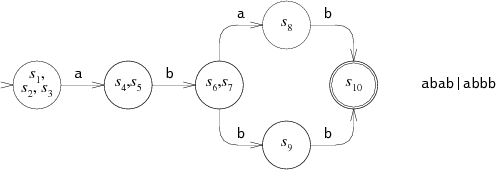
An example of recognition by the machine of a pattern corresponding to the regular expression A (BB) + A:

The state machine is always in one of the states designated as S 0 ... S 4 . When the machine reads the data, it enters the next state. There are two special states: S 0 - initial, S 4 - matching state (matching state).
The machine reads incoming data one character at a time, sequentially moving from one state to another, depending on the current character. Take the ABBBBA set. When the machine reads the first A, it is in the S0 state. Then goes to S1. Then the process is repeated as the rest of the characters are read: B - S 2 , B - S 3 , B - S 2 , B - S 3 and, finally, A - S 4 .
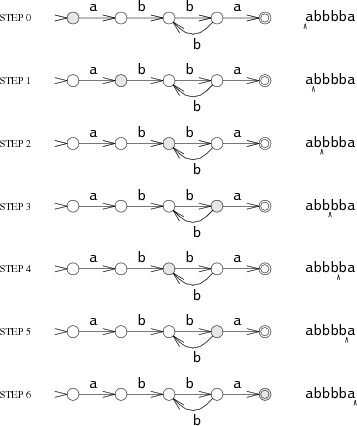
If the car stops in state S 4 , then the symbol is found; if in a different state - not found.
This type of machine is called a deterministic finite automaton (DFA, deterministic finite automaton), because regardless of the current state, each new input symbol leads to a transition to the next state. You can create a machine that will choose exactly what state to go to it.

This machine is similar to the previous one, but is not deterministic, because if B is read in the S 2 state, then the machine can go back to S 1 (hoping to get another BB) and S 3 (hoping to get the last A) . Since the machine does not know what other characters are included in the pattern, it cannot evaluate which decision will be correct. That is, she always guesses . Such machines are called non-deterministic (NFA or NDFA, nondeterministic finite automata). NFA finds a match if it can read a character and go into a matching state.
It is sometimes more convenient to allow NFA to change state at any time without reading incoming data. In the diagram, this is indicated by an unmarked transition (arrow without signatures). For example, this option will be the most advantageous in the case of the template A (BB) + A:
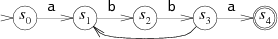
Functionally, they are absolutely equivalent. Each regular expression can be matched with equivalent NFA (they will look for the same patterns), and vice versa. There are different ways to convert regular expressions to NFA. One of these, described below, was proposed by Thompson in 1968.
Regular expression NFA is collected from partial NFA for each of the subexpressions, with a different construction for each operator. Partial NFA does not have a matching state; instead, it contains one or more "hanging" transitions. The build process is completed when these transitions result in a match state.
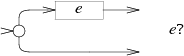
NFA search for single characters look like this:
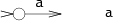
The NFA for the concatenation of E 1 E 2 consists of the machine E 1 , whose final transition is connected to the beginning of the machine E 2 :
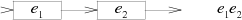
In NFA, for alternation E 1 | E 2 , a new initial state is added with the choice of following through the machine E 1 or E 2 :
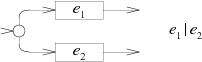
In NFA for E? Machine E alternates with a blank transition:
In NFA, for E *, the same rotation is used, but the E machine loops to the initial state:
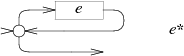
There is also a loop in NFA for E +, but in this case you need to go through E at least once:
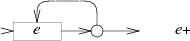
If you analyze the above schemes, you can see that for each character or metacharacter in a regular expression (except for parentheses) a separate state is created. Thus, the number of states of the resulting NFA is at least equal to the length of the original regular expression.
As in the case of the previously considered example of NFA, unmarked transitions can either not be used from the very beginning, or they can be removed after assembly. But their presence makes it easier for us to read and understand NFA, so we will keep them further.
Now we have a way to check if the PB contains a string: transform the regular expression into NFA and run it using the string as input. Remember that NFAs can well guess what state they should go to. To use NFA on a regular computer, you must select the appropriate algorithm.
For example, you can go through the options until you find the right one. Consider the NFA for ABAB | ABBB, performing a search on ABBB:
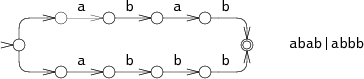
During action 0, the NFA must decide whether it should look for ABAB or ABBB. In our example, he chose the first option and failed during action 3. Then he tries to search for the second combination and finds during action 4. This approach has a recursive implementation and allows you to repeatedly read the data for a successful search. The machine should try all possible options before stopping the execution. In this example, only two branches are shown, but in life their number can grow exponentially, which greatly reduces the search performance.
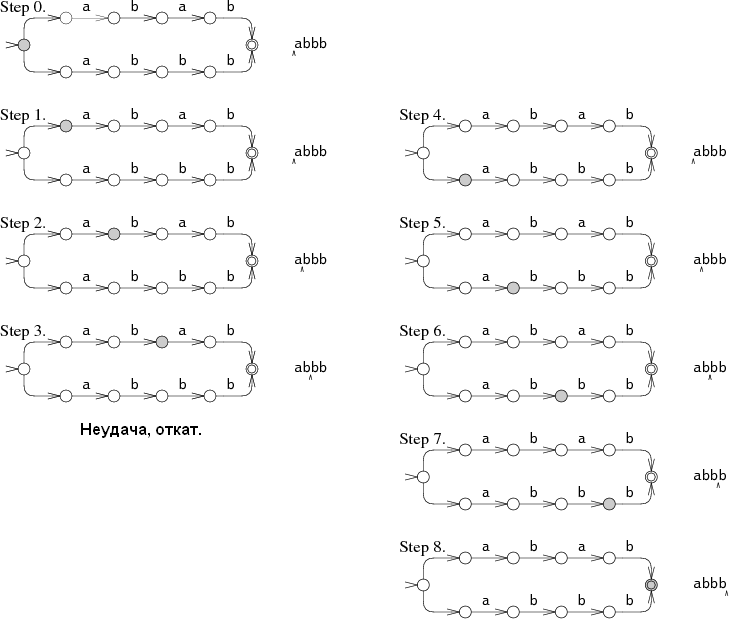
Another approach is more complicated, but more effective. We are talking about the simultaneous search for both templates. In this case, the machine can be in several different states at once. When processing each character, it goes through all the relevant states.
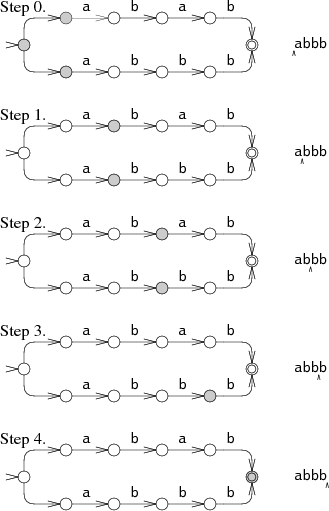
The execution of the machine begins simultaneously with the initial state and all other states to which unmarked transitions lead. During actions 1 and 2, the NFA is in two states at once. With this approach, data is read only once, and the machine simultaneously tries to go along two branches. In the most "neglected" cases, NFA can be in all states at the same time during each action. As a result, the search duration is very long regardless of the length of the template and templates of any size can be processed during linear time. This is a kind of compensation for the exponential operating time when using backtracking. Efficiency depends on the set of simultaneously available states, and not on the paths to them. If NFA consists of N nodes, then during each action a maximum of N states can be simultaneously, and the number of transitions can reach 2 N.
This approach — when the machine is simultaneously in several states — was proposed by Thompson in 1968. In his interpretation, each state was described by small pieces of machine code, and the list of possible states was a sequence of instructions for calling functions. In essence, Thompson compiled regular expressions into literate machine code. Today, 40 years later, computers are much more powerful, and it is not necessary to use machine code. Therefore, below is an implementation variant on ANSI C. The full code (less than 400 lines) and benchmark scripts can be downloaded from here: http://swtch.com/~rsc/regexp/ . If you are not friends with the C language, you can read the descriptions.
To begin with, compiling RVs to NFA equivalent. In our C code, NFA is represented as a related collection of State structures:
Each of them corresponds to one of the three subsequent NFA fragments:
lastlist is used at run time, its role will be explained below.
The compiler creates NFA from a regular expression in postfix notation with the addition of a dot (.), An explicit concatenation operator. The separate function re2post rewrites regular infix expressions like A (BB) + A in the form of equivalent postfix ABB expressions. +. A ...
In the "real" implementation, the dot should be used as a metacharacter "any character", and not as a concatenation operator. It is also possible that in a real situation NFA will have to be compiled during parsing, rather than creating an explicit postfix expression. But the postfix variant is more convenient and more in line with the approach proposed by Thompson.
As the postfix expression is scanned, the compiler creates a stack of computed NFA fragments. The presence of a literal constant leads to the addition of a new fragment, and each statement requires first removing the fragment from the stack, and then adding a new one. For example, after compiling ABB to ABB. +. A. NFA fragments for A, B and B appear on the stack. Compiling a point removes two fragments for B and adds a fragment for the BB ... concatenation. Each fragment is determined by the initial state and outgoing transitions:
Start denotes the initial state of the fragment, and out denotes a list of pointers to State * pointers, which do not yet lead anywhere. In the NFA fragment, they look like hanging transitions.
The list of pointers can be manipulated with the help of auxiliary instructions:
List1 creates a new list containing a single outp pointer. Append merges two lists and returns the result. Patch connects the trailing transitions in the list l with the state s: for each outp pointer in the list l is set * outp = s.
Based on these elements and the stack of fragments, a simple loop is created from the postfix expression. Finally, it remains to add one fragment: the state change completes the NFA.
Compilation steps corresponding to the conversion steps described earlier:
Character literals:
Catenation:
Alternation:
Zero or more:
One or more:
After creating the NFA, we need to model it. To do this, it is necessary to keep track of the sets of Sets, which are stored as a simple array list:
In the simulation uses two lists:
At the beginning of the run loop, only the initial state is entered into clist and the operation of the machine is initialized, one action at a time.
In order not to distribute at each iteration, match uses two predistributed lists l1 and l2 as clist and nlist.
If in the list of final states there is a coincidence state, then we have found the required set of characters:
A state is added to the list using addstate, but only if it is not yet in it. Scanning the list with each addition would be inefficient; instead, the listid variable is used to control the version of the list. When addstate adds the S state to the list, the listid value is written to s-> lastlist. If their values are equal, then, therefore, S is already in the list. If S is a Split state, from which unmarked transitions to new states are possible, then addstate adds these states to the list instead of S.
The list of initial states is created using the startlist:
Finally, step tells NFA to begin processing the next character, using the current clist to create the nlist:
The implementation described above cannot boast of high performance. But it happens that the slow implementation of the linear time algorithm easily circumvents the fast implementation of the exponential time algorithm if the exponent is large enough. This is well demonstrated when testing various popular engines on so-called pathological regular expressions.
Let's consider RV A? N A N. If a? allows you not to look for matches for any characters, then this PB will correspond to A N. In implementations of RV with backtracking when searching for 1-or-0? first, 1 will be searched, and then 0. The number of such choices can reach N, and the number of possibilities - 2 N. And only the most recent opportunity - the choice of 0 for all? - will lead to a coincidence. When using the backtracking method, execution takes O (2 N ) time, so that if N ≥ 25, the degree of scaling becomes small.
For comparison, with the length of the character set N, the Thompson algorithm also implies about N possible states, but performs a search in O (N 2 ) time. Since the constant RV is not preserved when the input data is increased, the execution time is described by a superlinear function. If the length of the PB is M, and the search is performed on the text of length N, then using the Thompson algorithm, the execution time is O (MN).
Match search A? N A N to A N (the size of the PB and the text is equal to N):
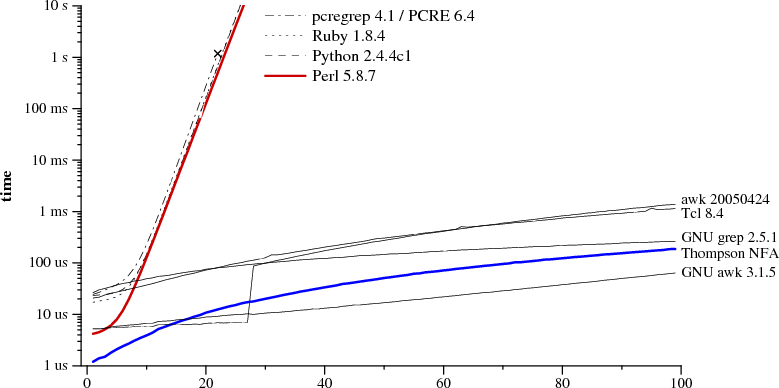
Note that the Y axis has a logarithmic scale. This is done for the convenience of displaying various implementations.
As you can see, recursive backtracking is used in Perl, Python, PCRE and Ruby. In PCRE, the correct result cannot be obtained already at N = 23 due to the interruption of backtracking due to the achievement of the maximum number of actions. In the Perl engine, the search is memorized , which can significantly reduce the time cost due to a slight increase in memory usage, despite the use of backlinks. But, as can be seen from the graph, the memoization here is incomplete: the execution time grows exponentially even in the absence of backlinks in expressions. In Java, although it is not depicted in the graph, backtracking implementation is also used. The java.util.regex interface requires backtracking, since arbitrary Java code can be inserted into the search path. And PHP uses the PCRE library.
The blue line on the graph shows the performance of the Thompson algorithm implemented in the C language. In awk, Tcl, GNU grep and GNU awk, the DFA is assembled and rendered on the fly, we will discuss this later.
Some would argue that this test is unfair to the implementation with backtracking, since the comparison is made on the example of a non-standard deadlock situation. But another thing is important: when there is a choice between a method that has a predictable execution time (and a short one) with all types of input data, and a method that usually has good performance, but in some cases may require thousands of machine hours, the solution should be obvious .
Yes, in practice, situations rarely occur in which search performance is so depressing. But there are still a lot of tasks in which the search speed is quite low. For example, when to get the five fields separated by a space, use (. *) (. *) (. *) (. *) (. *) Or alternations, where frequently encountered options are not at the beginning. As a result, programmers often have to learn which constructions are not too successful to avoid their use, or to use so-called optimizers . But when using the Thompson NFA algorithm, this is not required, there are no “expensive” regular expressions.
In terms of efficiency, DFA is superior to NFA, since they can only be in one state at a time. Any NFA can be converted to an equivalent DFA, in which each state corresponds to a list of NFA states.
Here is the above NFA for ABAB | ABBB:
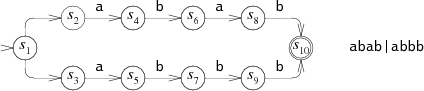
Equivalent DFA looks like this:
In some ways, Thompson NFA is equivalent to DFA: each List corresponds to one of the DFA states, and the step function, based on the list of states and the next search character, calculates the next DFA state. Thompson's algorithm models DFA, reconstructing each of the states as necessary. But instead of doing this after every action, we can cache all lists in the backup memory. This helps to further avoid redundant calculations, especially the calculations of the equivalent DFA. Let's look at this approach.
We need to add less than 100 lines to the above described NFA to make DFA. Before you implement the caching mechanism, you must first declare a new data type to describe the state of the DFA:
DState is a cached copy of the list l. The next array stores pointers to the next state for each possible input data character: if the current state is D and the next character is C, then the next state is d-> next [c]. If d-> next [c] is null, then the next state is not yet calculated. Nextstate is responsible for calculating, writing, and returning the next state.
When searching for a regular expression, d-> next [c] is processed cyclically, calling nextstate to compute the new state as needed.
All calculated DState must be saved as a structure that will allow to find them by the List criterion. For this, a binary tree is used, where sorted List is used as keys. By key, the dstate function returns the desired value:
Nextstate initializes the step NFA and returns the corresponding DState:
As with NFA, l1 is a predefined List.
Although DState values correspond to certain DFA states, DFA itself is built only when the need arises. If during the search the DFA status is detected, it means that it is not yet in the cache. As an alternative solution, the entire DFA can be calculated once. This will speed up the work of match somewhat, since the conditional transition will be eliminated, but it will increase the launch time and the amount of memory used.
When building a DFA on the fly, note the following point: memory allocation. Since DState is the step function cache, as dstate grows, the cache can decide to destroy the entire DFA. To implement such a cache replacement policy, only a few extra lines of code in dstate and nextstate are required, as well as another 50 lines for memory management. Download an example here: http://swtch.com/~rsc/regexp/ . By the way, awk uses a similar strategy, there are no more than 32 states stored in the cache. This explains the drop in its performance since N = 28, as was shown in the graph.
NFA obtained from regular expressions is distinguished by good locality: in most tests they take the same states and follow the same transitions over and over again. This further increases the importance of caching, because after the first pass, it is no longer necessary to calculate the states, it is enough to take them from memory. In DFA-based implementations, additional optimization can be applied, further increasing execution speed.
In these applications, it is somewhat harder to use regular expressions than in the implementations described above. Here we look at the characteristic difficulties encountered by developers.
Character classes They are a simplified representation of alternation - 0-9, \ w or. (point). At compile time, they can be converted to interlaces, although for their explicit representation it would be more efficient to add a new type of NFA node. POSIX defines special character classes like [[: upper:]], which change their meaning depending on the current node. The difficulty of working with them lies in defining their values, and not in putting these values into NFA.
Control sequences Regular expression syntax should handle escape sequences so that you can search for metacharacters (\ (, \), \\, etc.), as well as specify special characters like \ n.
Repeat (Counted repetition) . In many implementations of regular expressions, the repetition operator {N} is used, where N is the exact number of matches of the pattern. Writing {N, M} means that the pattern must be found from N to M times. {N,} - N and more times. In recursive backtracking implementations, repetitions can be performed using loops. In implementations based on NFA and DFA, repetitions should be presented in expanded form: instead of E {3} - EEE, instead of E {3,5} - EEEE? E?, Instead of E {3,} - EEE +.
Subexpressions (Submatch extraction) . If RVs are used to split or parse strings, it can be helpful to find out if there are matches with subexpressions in the input data. If in the text there is a coincidence with ([0-9] + - [0-9] + - [0-9] +) ([0-9] +: [0-9] +), then in many realizations of RT you can will find matches for each of the subexpressions enclosed in parentheses. For example, in Perl:
Extraction of subexpressions was largely ignored by theorists. Perhaps this is one of the main reasons for using recursive backtracking. However, variations of the Thompson algorithm can be adapted to work with subexpressions without losing performance. This was implemented as early as 1985, in the regexp library in the eighth version of UNIX, but was not widely used.
Unanchored matches . The information in this article is based on the fact that the search for PB is performed on all input data. But in life often there are situations when we need to find only part of the line that coincides with PB. In UNIX, the longest substring of matches found traditionally returns, starting closest to the beginning of the input data. Search without binding is a special case of subexpressions. It’s like looking for. * (E). *, Where the first sequence. * Limits the search to the shortest match.
Nasty operators . In the traditional UNIX implementation, using the repetition operators?, * And +, the maximum possible number of matches of the RVs is searched for. For example, if ABCD is searched with operators (. +) (. +), Then the first sequence (. +) Finds ABC and the second matches D. Such operators are called greedy.
Perl uses non-greedy versions ??, *? and + ... . Operator's greed does not affect the compliance of the RV with the entire line. It depends only on the choice of boundaries subexpressions. The backtracking algorithm allows the use of a simple implementation of non-operator operators: first, a shorter match is sought, then a longer one. For example, in the standard implementation, the algorithm with backtracking when searching for E? first tries to find E, and after detection tries not to use it anymore; with E ?? another procedure is applied. Variants of the Thompson algorithm using subexpressions can be adapted for the use of non-greedy operators.
Assertions (Assertions) . The ^ and $ metacharacters can be used as statements with respect to the text to the right and to the left of them. ^ says that the character in front of it is the beginning of a new line. $ states that the next character is the end of a line. Other statements have been added to Perl, for example, \ b - the previous character is alphanumeric, and the next is not, or vice versa. Also, Perl summarizes the idea of arbitrary conditions called preliminary statements (lookahead assertions): (? = Re) states that the text after the current position coincides with re, but does not change the position itself. (?! re) states that the text does not coincide with re, otherwise it works the same way. The statements (? <= Re) and (? <! Re) are equivalent and speak about the coincidence of the text before the current position.
Simple statements like ^, $ and \ b can be easily applied to NFA by delaying the matching procedure for preliminary statements by one byte. General statements are more difficult to apply in NFA, but still possible.
Backlinks (Backreferences). As mentioned above, no one has yet succeeded in effectively implementing RT with backlinks. On the other hand, no one has yet proved that this is impossible to do. This is an NP-complete task , and if someone finds a solution, he can get a prize of one million dollars . The easiest way is not to use backlinks at all, as did the awk and egrep developers. : , . POSIX . Thompson NFA, . .
. Perl . , , , . , . , :
. ASCII- Unicode. Plan 9 Unicode: NFA Unicode-. NFA , UTF-8 , Unicode.
, . Perl, PCRE, Python, Ruby, Java , , . ( ), .
[ 1 ] L. Peter Deutsch and Butler Lampson. An online editor // Communications of the ACM. Vol. 10, Iss. 12 (December 1967). P. 793–799. doi.acm.org/10.1145/363848.363863
[ 2 ] Ville Laurikari. NFAs with Tagged Transitions, their Conversion to Deterministic Automata and Application to Regular Expressions // Proceedings of the Symposium on String Processing and Information Retrieval. September 2000. laurikari.net/ville/spire2000-tnfa.pdf
[ 3 ] M. Douglas McIlroy. Enumerating the strings of regular languages // Journal of Functional Programming. 2004. № 14. P. 503–518. www.cs.dartmouth.edu/~doug/nfa.ps.gz (preprint)
[ 4 ] R. McNaughton and H. Yamada. Regular expressions and state graphs for automata // IRE Transactions on Electronic Computers. Vol. EC-9 (1) (March 1960). P. 39–47.
[ 5 ] Paul Pierce. CTSS source listings. www.piercefuller.com/library/ctss.html (Thompson's QED is in the file com5 in the source listings archive and is marked as 0QED)
[ 6 ] Rob Pike/ The text editor sam // Software — Practice & Experience. Vol. 17, № 11 (November 1987. P. 813–845. plan9.bell-labs.com/sys/doc/sam/sam.html
[ 7 ] Michael Rabin and Dana Scott. Finite automata and their decision problems // IBM Journal of Research and Development. 1959. № 3. P. 114–125. www.research.ibm.com/journal/rd/032/ibmrd0302C.pdf
[ 8 ] Dennis Ritchie. An incomplete history of the QED text editor. www.bell-labs.com/usr/dmr/www/qed.html
[ 9 ] Ken Thompson. Programming Techniques: Regular expression search algorithm // Communications of the ACM. Vol. 11, Iss. 6 (June 1968). P. 419–422. doi.acm.org/10.1145/363347.363387 ( PDF )
[ 10 ] Tom Van Vleck. The IBM 7094 and CTSS. www.multicians.org/thvv/7094.html


In the first case, the search takes A? n A n of time, in the second - A n .
')
The degrees denote the repeatability of rows, that is, A? 3 A 3 is the same as A? A? A? AAA. Charts reflect the time required to search through regular expressions.
Note that in Perl it takes more than 60 seconds to search for a string of 29 characters. And with the second method - 20 microseconds . It's not a mistake. When searching for the 29-character string, Thompson NFA runs about a million times faster. If you need to find a 100-character string, Thompson NFA can handle in less than 200 microseconds, and Perl will need more than 10 to 15 years. Moreover, it is taken only as an example, in many other languages the same picture is observed - in Python, PHP, Ruby, etc. Below we consider this question in more detail.
Surely you find it hard to believe the given data. If you’ve worked with Perl, you’d hardly notice its poor performance when working with regular expressions. The fact is that in most cases, Perl handles them fairly quickly. However, as follows from the graph, you can encounter the so-called pathological regular expressions, on which Perl begins to slip. At the same time, Thompson NFA has no such problem.
A logical question arises: why not use the Thompson NFA method in Perl? This is possible and should be done, and this will be discussed further.
Previously, regular expressions were a vivid illustration of how the use of the “good theory” can lead to the creation of good programs. Originally, they were created as a simple theoretical computational model, and then Ken Thompson implemented them in one of the versions of the QED text editor for CTSS. Dennis Ritchie did the same in his own version of QED for GE-TSS. Later, Thompson and Ritchie had a hand in creating UNIX, moving regular expressions there as well. In the late 1970s, they were one of the main features of this OS and were used in tools such as ed, sed, grep, egrep, awk and lex.
Today, regular expressions provide a no less vivid illustration of how ignoring the “good theory” leads to the creation of bad programs. Implementations of regular expressions in many modern tools work much slower than those used 30 years ago in UNIX tools.
In this article, we will look at various aspects of the “good theory”, as well as its practical implementation of the Thompson algorithm. It consists of less than 400 lines of C and is very close to that used in Perl, Python, PCRE and a number of other languages.
Regular expressions
This is the name used to describe string data patterns. If a certain set of string data is similar to that described by a regular expression (RV), then we are talking about the coincidence of the RV with this string data.
The simplest case of a regular expression is a single letter character. With the exception of metacharacters - *, +,?, (,), And |, - all characters are equal to themselves. To search for matches with metacharacters, you need to add a backslash: the combination of characters \ + is similar to +.
Two regular expressions can be transformed or combined, creating a new regular expression: if E 1 matches S, and E 2 matches t, then E 1 | E 2 matches S or T, and E 1 E 2 corresponds to ST.
Metacharacters *, + and? are loop operators:
- E 1 * says that E 1 can occur 0 or more times;
- E 1 + says that E 1 can occur 1 or more times;
- E 1 ? says that E 1 can occur 0 or 1 times.
Operators are prioritized by increasing the degree of binding (binding): first, alternation, then concatenation, and, finally, repetition operators. Parentheses can be used to distinguish subexpressions, like arithmetic ones: AB | cd corresponds to (AB) | (cd), AB * corresponds to A (B *).
The syntax described is a subset of the syntax used in egrep. This is enough to describe all regular languages (regular languages). Roughly speaking, a regular language is a set of lines that can be found in the text in one pass using a fixed amount of memory. Modern implementations of regular expressions (in Perl and several other languages) use numerous new operators and control sequences . This makes PB more concise, and sometimes quite incomprehensible. But efficiency is not added, since almost all of these new expressions can be expressed using the “traditional” syntax, just in a longer form.
Additional features provide so-called feedbacks (backreferences). The back reference \ 1 or \ 2 corresponds to a line similar to the previous expression enclosed in parentheses. (cat | dog) \ 1 matches catcat and dogdog, not catdog or dogcat.
From the point of view of the theory, regular expressions with feedback are no longer regular expressions. The use of backlinks has its considerable price: in different implementations it is necessary to use exponential search algorithms. Of course, Perl (like other languages) cannot be relieved of feedback support. But in their absence, you can use much faster algorithms.
Finite automata
State machines can be used to describe patterns. They are also known as state machines. In this article, the concepts of "automatic" and "machine" will be interchangeable.
An example of recognition by the machine of a pattern corresponding to the regular expression A (BB) + A:

The state machine is always in one of the states designated as S 0 ... S 4 . When the machine reads the data, it enters the next state. There are two special states: S 0 - initial, S 4 - matching state (matching state).
The machine reads incoming data one character at a time, sequentially moving from one state to another, depending on the current character. Take the ABBBBA set. When the machine reads the first A, it is in the S0 state. Then goes to S1. Then the process is repeated as the rest of the characters are read: B - S 2 , B - S 3 , B - S 2 , B - S 3 and, finally, A - S 4 .

If the car stops in state S 4 , then the symbol is found; if in a different state - not found.
This type of machine is called a deterministic finite automaton (DFA, deterministic finite automaton), because regardless of the current state, each new input symbol leads to a transition to the next state. You can create a machine that will choose exactly what state to go to it.

This machine is similar to the previous one, but is not deterministic, because if B is read in the S 2 state, then the machine can go back to S 1 (hoping to get another BB) and S 3 (hoping to get the last A) . Since the machine does not know what other characters are included in the pattern, it cannot evaluate which decision will be correct. That is, she always guesses . Such machines are called non-deterministic (NFA or NDFA, nondeterministic finite automata). NFA finds a match if it can read a character and go into a matching state.
It is sometimes more convenient to allow NFA to change state at any time without reading incoming data. In the diagram, this is indicated by an unmarked transition (arrow without signatures). For example, this option will be the most advantageous in the case of the template A (BB) + A:
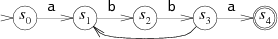
Converting Regular Expressions to NFA
Functionally, they are absolutely equivalent. Each regular expression can be matched with equivalent NFA (they will look for the same patterns), and vice versa. There are different ways to convert regular expressions to NFA. One of these, described below, was proposed by Thompson in 1968.
Regular expression NFA is collected from partial NFA for each of the subexpressions, with a different construction for each operator. Partial NFA does not have a matching state; instead, it contains one or more "hanging" transitions. The build process is completed when these transitions result in a match state.
NFA search for single characters look like this:
The NFA for the concatenation of E 1 E 2 consists of the machine E 1 , whose final transition is connected to the beginning of the machine E 2 :
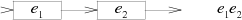
In NFA, for alternation E 1 | E 2 , a new initial state is added with the choice of following through the machine E 1 or E 2 :

In NFA for E? Machine E alternates with a blank transition:

In NFA, for E *, the same rotation is used, but the E machine loops to the initial state:

There is also a loop in NFA for E +, but in this case you need to go through E at least once:

If you analyze the above schemes, you can see that for each character or metacharacter in a regular expression (except for parentheses) a separate state is created. Thus, the number of states of the resulting NFA is at least equal to the length of the original regular expression.
As in the case of the previously considered example of NFA, unmarked transitions can either not be used from the very beginning, or they can be removed after assembly. But their presence makes it easier for us to read and understand NFA, so we will keep them further.
Regular expression search algorithms
Now we have a way to check if the PB contains a string: transform the regular expression into NFA and run it using the string as input. Remember that NFAs can well guess what state they should go to. To use NFA on a regular computer, you must select the appropriate algorithm.
For example, you can go through the options until you find the right one. Consider the NFA for ABAB | ABBB, performing a search on ABBB:


During action 0, the NFA must decide whether it should look for ABAB or ABBB. In our example, he chose the first option and failed during action 3. Then he tries to search for the second combination and finds during action 4. This approach has a recursive implementation and allows you to repeatedly read the data for a successful search. The machine should try all possible options before stopping the execution. In this example, only two branches are shown, but in life their number can grow exponentially, which greatly reduces the search performance.
Another approach is more complicated, but more effective. We are talking about the simultaneous search for both templates. In this case, the machine can be in several different states at once. When processing each character, it goes through all the relevant states.

The execution of the machine begins simultaneously with the initial state and all other states to which unmarked transitions lead. During actions 1 and 2, the NFA is in two states at once. With this approach, data is read only once, and the machine simultaneously tries to go along two branches. In the most "neglected" cases, NFA can be in all states at the same time during each action. As a result, the search duration is very long regardless of the length of the template and templates of any size can be processed during linear time. This is a kind of compensation for the exponential operating time when using backtracking. Efficiency depends on the set of simultaneously available states, and not on the paths to them. If NFA consists of N nodes, then during each action a maximum of N states can be simultaneously, and the number of transitions can reach 2 N.
Implementation
This approach — when the machine is simultaneously in several states — was proposed by Thompson in 1968. In his interpretation, each state was described by small pieces of machine code, and the list of possible states was a sequence of instructions for calling functions. In essence, Thompson compiled regular expressions into literate machine code. Today, 40 years later, computers are much more powerful, and it is not necessary to use machine code. Therefore, below is an implementation variant on ANSI C. The full code (less than 400 lines) and benchmark scripts can be downloaded from here: http://swtch.com/~rsc/regexp/ . If you are not friends with the C language, you can read the descriptions.
Implementation: Compiled in NFA
To begin with, compiling RVs to NFA equivalent. In our C code, NFA is represented as a related collection of State structures:
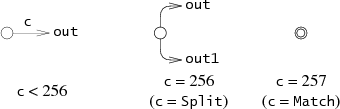
struct State { int c; State *out; State *out1; int lastlist; }; Each of them corresponds to one of the three subsequent NFA fragments:

lastlist is used at run time, its role will be explained below.
The compiler creates NFA from a regular expression in postfix notation with the addition of a dot (.), An explicit concatenation operator. The separate function re2post rewrites regular infix expressions like A (BB) + A in the form of equivalent postfix ABB expressions. +. A ...
In the "real" implementation, the dot should be used as a metacharacter "any character", and not as a concatenation operator. It is also possible that in a real situation NFA will have to be compiled during parsing, rather than creating an explicit postfix expression. But the postfix variant is more convenient and more in line with the approach proposed by Thompson.
As the postfix expression is scanned, the compiler creates a stack of computed NFA fragments. The presence of a literal constant leads to the addition of a new fragment, and each statement requires first removing the fragment from the stack, and then adding a new one. For example, after compiling ABB to ABB. +. A. NFA fragments for A, B and B appear on the stack. Compiling a point removes two fragments for B and adds a fragment for the BB ... concatenation. Each fragment is determined by the initial state and outgoing transitions:
struct Frag { State *start; Ptrlist *out; }; Start denotes the initial state of the fragment, and out denotes a list of pointers to State * pointers, which do not yet lead anywhere. In the NFA fragment, they look like hanging transitions.
The list of pointers can be manipulated with the help of auxiliary instructions:
Ptrlist *list1(State **outp); Ptrlist *append(Ptrlist *l1, Ptrlist *l2); void patch(Ptrlist *l, State *s); List1 creates a new list containing a single outp pointer. Append merges two lists and returns the result. Patch connects the trailing transitions in the list l with the state s: for each outp pointer in the list l is set * outp = s.
Based on these elements and the stack of fragments, a simple loop is created from the postfix expression. Finally, it remains to add one fragment: the state change completes the NFA.
State* post2nfa(char *postfix) { char *p; Frag stack[1000], *stackp, e1, e2, e; State *s; #define push(s) *stackp++ = s #define pop() *--stackp stackp = stack; for(p=postfix; *p; p++){ switch(*p){ /* compilation cases, described below */ } } e = pop(); patch(e.out, matchstate); return e.start; } Compilation steps corresponding to the conversion steps described earlier:
Character literals:
default: s = state(*p, NULL, NULL); push(frag(s, list1(&s->out)); break; Catenation:
case '.': e2 = pop(); e1 = pop(); patch(e1.out, e2.start); push(frag(e1.start, e2.out)); break; Alternation:
case '|': e2 = pop(); e1 = pop(); s = state(Split, e1.start, e2.start); push(frag(s, append(e1.out, e2.out))); break; Zero or more:
case '*': e = pop(); s = state(Split, e.start, NULL); patch(e.out, s); push(frag(s, list1(&s->out1))); break; One or more:
case '+': e = pop(); s = state(Split, e.start, NULL); patch(e.out, s); push(frag(e.start, list1(&s->out1))); break; Implementation: NFA simulation
After creating the NFA, we need to model it. To do this, it is necessary to keep track of the sets of Sets, which are stored as a simple array list:
struct List { State **s; int n; }; In the simulation uses two lists:
- clist - the current set of states in which the NFA is located;
- nlist is the next set of states that NFA will go to after processing the current symbol.
At the beginning of the run loop, only the initial state is entered into clist and the operation of the machine is initialized, one action at a time.
int match(State *start, char *s) { List *clist, *nlist, *t; /* l1 and l2 are preallocated globals */ clist = startlist(start, &l1); nlist = &l2; for(; *s; s++){ step(clist, *s, nlist); t = clist; clist = nlist; nlist = t; /* swap clist, nlist */ } return ismatch(clist); } In order not to distribute at each iteration, match uses two predistributed lists l1 and l2 as clist and nlist.
If in the list of final states there is a coincidence state, then we have found the required set of characters:
int ismatch(List *l) { int i; for(i=0; i<l->n; i++) if(l->s[i] == matchstate) return 1; return 0; } A state is added to the list using addstate, but only if it is not yet in it. Scanning the list with each addition would be inefficient; instead, the listid variable is used to control the version of the list. When addstate adds the S state to the list, the listid value is written to s-> lastlist. If their values are equal, then, therefore, S is already in the list. If S is a Split state, from which unmarked transitions to new states are possible, then addstate adds these states to the list instead of S.
void addstate(List *l, State *s) { if(s == NULL || s->lastlist == listid) return; s->lastlist = listid; if(s->c == Split){ /* follow unlabeled arrows */ addstate(l, s->out); addstate(l, s->out1); return; } l->s[l->n++] = s; } The list of initial states is created using the startlist:
List* startlist(State *s, List *l) { listid++; l->n = 0; addstate(l, s); return l; } Finally, step tells NFA to begin processing the next character, using the current clist to create the nlist:
void step(List *clist, int c, List *nlist) { int i; State *s; listid++; nlist->n = 0; for(i=0; i<clist->n; i++){ s = clist->s[i]; if(s->c == c) addstate(nlist, s->out); } } Performance
The implementation described above cannot boast of high performance. But it happens that the slow implementation of the linear time algorithm easily circumvents the fast implementation of the exponential time algorithm if the exponent is large enough. This is well demonstrated when testing various popular engines on so-called pathological regular expressions.
Let's consider RV A? N A N. If a? allows you not to look for matches for any characters, then this PB will correspond to A N. In implementations of RV with backtracking when searching for 1-or-0? first, 1 will be searched, and then 0. The number of such choices can reach N, and the number of possibilities - 2 N. And only the most recent opportunity - the choice of 0 for all? - will lead to a coincidence. When using the backtracking method, execution takes O (2 N ) time, so that if N ≥ 25, the degree of scaling becomes small.
For comparison, with the length of the character set N, the Thompson algorithm also implies about N possible states, but performs a search in O (N 2 ) time. Since the constant RV is not preserved when the input data is increased, the execution time is described by a superlinear function. If the length of the PB is M, and the search is performed on the text of length N, then using the Thompson algorithm, the execution time is O (MN).
Match search A? N A N to A N (the size of the PB and the text is equal to N):

Note that the Y axis has a logarithmic scale. This is done for the convenience of displaying various implementations.
As you can see, recursive backtracking is used in Perl, Python, PCRE and Ruby. In PCRE, the correct result cannot be obtained already at N = 23 due to the interruption of backtracking due to the achievement of the maximum number of actions. In the Perl engine, the search is memorized , which can significantly reduce the time cost due to a slight increase in memory usage, despite the use of backlinks. But, as can be seen from the graph, the memoization here is incomplete: the execution time grows exponentially even in the absence of backlinks in expressions. In Java, although it is not depicted in the graph, backtracking implementation is also used. The java.util.regex interface requires backtracking, since arbitrary Java code can be inserted into the search path. And PHP uses the PCRE library.
The blue line on the graph shows the performance of the Thompson algorithm implemented in the C language. In awk, Tcl, GNU grep and GNU awk, the DFA is assembled and rendered on the fly, we will discuss this later.
Some would argue that this test is unfair to the implementation with backtracking, since the comparison is made on the example of a non-standard deadlock situation. But another thing is important: when there is a choice between a method that has a predictable execution time (and a short one) with all types of input data, and a method that usually has good performance, but in some cases may require thousands of machine hours, the solution should be obvious .
Yes, in practice, situations rarely occur in which search performance is so depressing. But there are still a lot of tasks in which the search speed is quite low. For example, when to get the five fields separated by a space, use (. *) (. *) (. *) (. *) (. *) Or alternations, where frequently encountered options are not at the beginning. As a result, programmers often have to learn which constructions are not too successful to avoid their use, or to use so-called optimizers . But when using the Thompson NFA algorithm, this is not required, there are no “expensive” regular expressions.
NFA caching to build DFA
In terms of efficiency, DFA is superior to NFA, since they can only be in one state at a time. Any NFA can be converted to an equivalent DFA, in which each state corresponds to a list of NFA states.
Here is the above NFA for ABAB | ABBB:

Equivalent DFA looks like this:

In some ways, Thompson NFA is equivalent to DFA: each List corresponds to one of the DFA states, and the step function, based on the list of states and the next search character, calculates the next DFA state. Thompson's algorithm models DFA, reconstructing each of the states as necessary. But instead of doing this after every action, we can cache all lists in the backup memory. This helps to further avoid redundant calculations, especially the calculations of the equivalent DFA. Let's look at this approach.
We need to add less than 100 lines to the above described NFA to make DFA. Before you implement the caching mechanism, you must first declare a new data type to describe the state of the DFA:
struct DState { List l; DState *next[256]; DState *left; DState *right; }; DState is a cached copy of the list l. The next array stores pointers to the next state for each possible input data character: if the current state is D and the next character is C, then the next state is d-> next [c]. If d-> next [c] is null, then the next state is not yet calculated. Nextstate is responsible for calculating, writing, and returning the next state.
When searching for a regular expression, d-> next [c] is processed cyclically, calling nextstate to compute the new state as needed.
int match(DState *start, char *s) { int c; DState *d, *next; d = start; for(; *s; s++){ c = *s & 0xFF; if((next = d->next[c]) == NULL) next = nextstate(d, c); d = next; } return ismatch(&d->l); } All calculated DState must be saved as a structure that will allow to find them by the List criterion. For this, a binary tree is used, where sorted List is used as keys. By key, the dstate function returns the desired value:
DState* dstate(List *l) { int i; DState **dp, *d; static DState *alldstates; qsort(l->s, l->n, sizeof l->s[0], ptrcmp); /* look in tree for existing DState */ dp = &alldstates; while((d = *dp) != NULL){ i = listcmp(l, &d->l); if(i < 0) dp = &d->left; else if(i > 0) dp = &d->right; else return d; } /* allocate, initialize new DState */ d = malloc(sizeof *d + l->n*sizeof l->s[0]); memset(d, 0, sizeof *d); d->ls = (State**)(d+1); memmove(d->ls, l->s, l->n*sizeof l->s[0]); d->ln = l->n; /* insert in tree */ *dp = d; return d; } Nextstate initializes the step NFA and returns the corresponding DState:
DState* nextstate(DState *d, int c) { step(&d->l, c, &l1); return d->next[c] = dstate(&l1); } NFA, DFA DState: DState* startdstate(State *start) { return dstate(startlist(start, &l1)); } As with NFA, l1 is a predefined List.
Although DState values correspond to certain DFA states, DFA itself is built only when the need arises. If during the search the DFA status is detected, it means that it is not yet in the cache. As an alternative solution, the entire DFA can be calculated once. This will speed up the work of match somewhat, since the conditional transition will be eliminated, but it will increase the launch time and the amount of memory used.
When building a DFA on the fly, note the following point: memory allocation. Since DState is the step function cache, as dstate grows, the cache can decide to destroy the entire DFA. To implement such a cache replacement policy, only a few extra lines of code in dstate and nextstate are required, as well as another 50 lines for memory management. Download an example here: http://swtch.com/~rsc/regexp/ . By the way, awk uses a similar strategy, there are no more than 32 states stored in the cache. This explains the drop in its performance since N = 28, as was shown in the graph.
NFA obtained from regular expressions is distinguished by good locality: in most tests they take the same states and follow the same transitions over and over again. This further increases the importance of caching, because after the first pass, it is no longer necessary to calculate the states, it is enough to take them from memory. In DFA-based implementations, additional optimization can be applied, further increasing execution speed.
Real examples of regular expressions
In these applications, it is somewhat harder to use regular expressions than in the implementations described above. Here we look at the characteristic difficulties encountered by developers.
Character classes They are a simplified representation of alternation - 0-9, \ w or. (point). At compile time, they can be converted to interlaces, although for their explicit representation it would be more efficient to add a new type of NFA node. POSIX defines special character classes like [[: upper:]], which change their meaning depending on the current node. The difficulty of working with them lies in defining their values, and not in putting these values into NFA.
Control sequences Regular expression syntax should handle escape sequences so that you can search for metacharacters (\ (, \), \\, etc.), as well as specify special characters like \ n.
Repeat (Counted repetition) . In many implementations of regular expressions, the repetition operator {N} is used, where N is the exact number of matches of the pattern. Writing {N, M} means that the pattern must be found from N to M times. {N,} - N and more times. In recursive backtracking implementations, repetitions can be performed using loops. In implementations based on NFA and DFA, repetitions should be presented in expanded form: instead of E {3} - EEE, instead of E {3,5} - EEEE? E?, Instead of E {3,} - EEE +.
Subexpressions (Submatch extraction) . If RVs are used to split or parse strings, it can be helpful to find out if there are matches with subexpressions in the input data. If in the text there is a coincidence with ([0-9] + - [0-9] + - [0-9] +) ([0-9] +: [0-9] +), then in many realizations of RT you can will find matches for each of the subexpressions enclosed in parentheses. For example, in Perl:
if(/([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+)/){ print "date: $1, time: $2\n"; } Extraction of subexpressions was largely ignored by theorists. Perhaps this is one of the main reasons for using recursive backtracking. However, variations of the Thompson algorithm can be adapted to work with subexpressions without losing performance. This was implemented as early as 1985, in the regexp library in the eighth version of UNIX, but was not widely used.
Unanchored matches . The information in this article is based on the fact that the search for PB is performed on all input data. But in life often there are situations when we need to find only part of the line that coincides with PB. In UNIX, the longest substring of matches found traditionally returns, starting closest to the beginning of the input data. Search without binding is a special case of subexpressions. It’s like looking for. * (E). *, Where the first sequence. * Limits the search to the shortest match.
Nasty operators . In the traditional UNIX implementation, using the repetition operators?, * And +, the maximum possible number of matches of the RVs is searched for. For example, if ABCD is searched with operators (. +) (. +), Then the first sequence (. +) Finds ABC and the second matches D. Such operators are called greedy.
Perl uses non-greedy versions ??, *? and + ... . Operator's greed does not affect the compliance of the RV with the entire line. It depends only on the choice of boundaries subexpressions. The backtracking algorithm allows the use of a simple implementation of non-operator operators: first, a shorter match is sought, then a longer one. For example, in the standard implementation, the algorithm with backtracking when searching for E? first tries to find E, and after detection tries not to use it anymore; with E ?? another procedure is applied. Variants of the Thompson algorithm using subexpressions can be adapted for the use of non-greedy operators.
Assertions (Assertions) . The ^ and $ metacharacters can be used as statements with respect to the text to the right and to the left of them. ^ says that the character in front of it is the beginning of a new line. $ states that the next character is the end of a line. Other statements have been added to Perl, for example, \ b - the previous character is alphanumeric, and the next is not, or vice versa. Also, Perl summarizes the idea of arbitrary conditions called preliminary statements (lookahead assertions): (? = Re) states that the text after the current position coincides with re, but does not change the position itself. (?! re) states that the text does not coincide with re, otherwise it works the same way. The statements (? <= Re) and (? <! Re) are equivalent and speak about the coincidence of the text before the current position.
Simple statements like ^, $ and \ b can be easily applied to NFA by delaying the matching procedure for preliminary statements by one byte. General statements are more difficult to apply in NFA, but still possible.
Backlinks (Backreferences). As mentioned above, no one has yet succeeded in effectively implementing RT with backlinks. On the other hand, no one has yet proved that this is impossible to do. This is an NP-complete task , and if someone finds a solution, he can get a prize of one million dollars . The easiest way is not to use backlinks at all, as did the awk and egrep developers. : , . POSIX . Thompson NFA, . .
. Perl . , , , . , . , :
$ perl -e '("a" x 100000) =~ /^(ab?)*$/;' Segmentation fault (core dumped) $ . ASCII- Unicode. Plan 9 Unicode: NFA Unicode-. NFA , UTF-8 , Unicode.
Conclusion
, . Perl, PCRE, Python, Ruby, Java , , . ( ), .
[ 1 ] L. Peter Deutsch and Butler Lampson. An online editor // Communications of the ACM. Vol. 10, Iss. 12 (December 1967). P. 793–799. doi.acm.org/10.1145/363848.363863
[ 2 ] Ville Laurikari. NFAs with Tagged Transitions, their Conversion to Deterministic Automata and Application to Regular Expressions // Proceedings of the Symposium on String Processing and Information Retrieval. September 2000. laurikari.net/ville/spire2000-tnfa.pdf
[ 3 ] M. Douglas McIlroy. Enumerating the strings of regular languages // Journal of Functional Programming. 2004. № 14. P. 503–518. www.cs.dartmouth.edu/~doug/nfa.ps.gz (preprint)
[ 4 ] R. McNaughton and H. Yamada. Regular expressions and state graphs for automata // IRE Transactions on Electronic Computers. Vol. EC-9 (1) (March 1960). P. 39–47.
[ 5 ] Paul Pierce. CTSS source listings. www.piercefuller.com/library/ctss.html (Thompson's QED is in the file com5 in the source listings archive and is marked as 0QED)
[ 6 ] Rob Pike/ The text editor sam // Software — Practice & Experience. Vol. 17, № 11 (November 1987. P. 813–845. plan9.bell-labs.com/sys/doc/sam/sam.html
[ 7 ] Michael Rabin and Dana Scott. Finite automata and their decision problems // IBM Journal of Research and Development. 1959. № 3. P. 114–125. www.research.ibm.com/journal/rd/032/ibmrd0302C.pdf
[ 8 ] Dennis Ritchie. An incomplete history of the QED text editor. www.bell-labs.com/usr/dmr/www/qed.html
[ 9 ] Ken Thompson. Programming Techniques: Regular expression search algorithm // Communications of the ACM. Vol. 11, Iss. 6 (June 1968). P. 419–422. doi.acm.org/10.1145/363347.363387 ( PDF )
[ 10 ] Tom Van Vleck. The IBM 7094 and CTSS. www.multicians.org/thvv/7094.html
Source: https://habr.com/ru/post/270507/
All Articles