Java Gauss Method
The article is devoted to the implementation of the Gauss algorithm for solving a system of linear algebraic equations in the Java language.
Consider the mathematical theory. A system of linear equations can have one solution, infinitely many solutions, or be inconsistent (not have solutions). Not all methods of solving SLAE can cope with the second case when the system has infinitely many solutions. For example, the Kramer method and the matrix method are not applicable, but the Gauss method may well be used.
The algorithm can be divided into two stages:
')
In the first stage, zeros are formed below or above the main diagonal, due to the use of elementary matrix transformations . At the second stage, unknowns are found starting from the end. Detailed theory can be viewed at the link: Gauss method , so with theory, perhaps all. Let's turn to implementation.
Let's start with the problem statement:
Let's start by writing an interface that should implement each equation:
Everything should be clear here, N is some successor to Number 'a, T is some type that implements this interface (recursive generics). The addEquation (T item) method allows you to add each element of the item equation to each of its elements. The remaining methods work similarly.
Now consider the class of the system of equations. As can be seen in the listing below, it is genericized in the same way as the Gauss interface and contains methods for conveniently accessing a private list of the containing equations.
Now we can begin to implement the "special case" of the structure of the equation. Create a class MyEquation that implements our interface. Let the Number’s successor be theultra-precise Float class (in practice, it’s better to take a Double ). Notice that the addEquation (MyEquation item) method uses a ListIterator class object that allows you to change the elements of the enumerated list.
Now we have a complete data structure that implements the system of equations. We create an algorithm that will take some object that implements the Gauss interface, then calling the necessary methods will lead the matrix to the desired form.
The algorithm is simple, find the desired coefficient, multiply the ith row (i = 0..n-1), and add it to the jth row (j = i..n). Note that the algorithm does not know exactly how the methods findCoefficient , mul and addEquation are implemented , this gives the code more flexibility, since if it is necessary to change the ways of manipulating equations (strings), only the implementations of the three aforementioned methods will be changed, and the main algorithm will remain intact.
Almost all. It remains to run all this in the main method:
Let's launch this miracle to check the correctness of the work ...
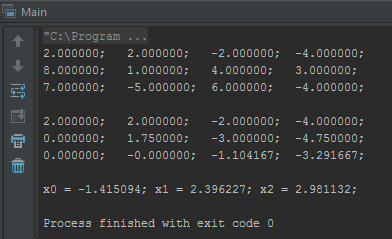
It's all. Sources can be downloaded on github.
The Gauss method is not very amenable to generalized programming (as you can see, the reverse is done separately), but there was a kind of implementation that I hope will help someone better understand the art of using interfaces and generics.
Theoretical information
Consider the mathematical theory. A system of linear equations can have one solution, infinitely many solutions, or be inconsistent (not have solutions). Not all methods of solving SLAE can cope with the second case when the system has infinitely many solutions. For example, the Kramer method and the matrix method are not applicable, but the Gauss method may well be used.
The algorithm can be divided into two stages:
')
- Direct move
- Reverse
In the first stage, zeros are formed below or above the main diagonal, due to the use of elementary matrix transformations . At the second stage, unknowns are found starting from the end. Detailed theory can be viewed at the link: Gauss method , so with theory, perhaps all. Let's turn to implementation.
Implementation
Let's start with the problem statement:
- we need to create a program that implements a system of linear equations in the form of a certain data structure using the techniques of generalized programming. The system should contain coefficients of the derived type from the Number class (i.e. Float , Integer , Double , etc.)
- Program the algorithm that, when inputting the data structure of the system, forms zeros below the main diagonal
Let's start by writing an interface that should implement each equation:
package gauss; public interface Gauss<N extends Number, T extends Gauss<N, T>> { public void addEquation(T item); public void mul(N coefficient); public N findCoefficient(N a, N b); public N at(int index); public int size(); } Everything should be clear here, N is some successor to Number 'a, T is some type that implements this interface (recursive generics). The addEquation (T item) method allows you to add each element of the item equation to each of its elements. The remaining methods work similarly.
Now consider the class of the system of equations. As can be seen in the listing below, it is genericized in the same way as the Gauss interface and contains methods for conveniently accessing a private list of the containing equations.
package gauss; import java.util.ArrayList; import java.util.List; public class LinearSystem<N extends Number, T extends Gauss<N, T>> { private List<T> list = new ArrayList<T>(); public T get(int index){ return list.get(index); } public void push(T elem){ list.add(elem); } public int size(){ return list.size(); } public N itemAt(int i, int j){ return list.get(i).at(j); } } Now we can begin to implement the "special case" of the structure of the equation. Create a class MyEquation that implements our interface. Let the Number’s successor be the
package gauss; import java.util.ArrayList; import java.util.List; import java.util.ListIterator; import java.util.Random; public class MyEquation implements Gauss<Float, MyEquation> { private List<Float> equation = new ArrayList<Float>(); public List<Float> getEquation(){ return equation; } public void generate(int size){ if (size < 2) size = 2; this.equation.clear(); for (int i = 0; i < size; i++){ Random random = new Random(); this.equation.add((float) (random.nextInt()%10) + 1); } } @Override public int size(){ return equation.size(); } @Override public void addEquation(MyEquation item){ ListIterator<Float> i = equation.listIterator(); ListIterator<Float> j = item.getEquation().listIterator(); for(; i.hasNext() && j.hasNext();){ Float a = i.next(); Float b = j.next(); i.set(a + b); } } @Override public void mul(Float coefficient){ for(ListIterator<Float> i = equation.listIterator(); i.hasNext();){ Float next = i.next(); i.set(next * coefficient); } } @Override public Float findCoefficient(Float a, Float b){ if (a == 0.0f) return 1.0f; return -b/a; } @Override public Float at(int index){ return equation.get(index); } } Now we have a complete data structure that implements the system of equations. We create an algorithm that will take some object that implements the Gauss interface, then calling the necessary methods will lead the matrix to the desired form.
package gauss; public class Algorithm<N extends Number, T extends Gauss<N, T>> { LinearSystem<N, T> list = null; public Algorithm(LinearSystem<N, T> system){ list = system; } public void calculate() throws NullPointerException, ArithmeticException{ if (list == null){ throw new NullPointerException("LinearSystem<N, T> instance equal null"); } if (!checkSystem(list)){ throw new ArithmeticException("Incorrect system for Gauss Method"); } for(int i = 0; i < list.size() - 1; i++){ for(int j = i + 1; j < list.size(); j++){ N k = list.get(j).findCoefficient(list.get(j).at(i), list.get(i).at(i)); list.get(j).mul(k); list.get(j).addEquation(list.get(i)); } } } private boolean checkSystem(LinearSystem<N, T> system){ if (system.size() < 2) return false; for(int i = 0; i < system.size(); i++){ if (system.get(i).size() != (system.size() + 1)){ return false; } } return true; } } The algorithm is simple, find the desired coefficient, multiply the ith row (i = 0..n-1), and add it to the jth row (j = i..n). Note that the algorithm does not know exactly how the methods findCoefficient , mul and addEquation are implemented , this gives the code more flexibility, since if it is necessary to change the ways of manipulating equations (strings), only the implementations of the three aforementioned methods will be changed, and the main algorithm will remain intact.
Almost all. It remains to run all this in the main method:
import gauss.Algorithm; import gauss.MyEquation; import gauss.LinearSystem; public class Main { private static final int DEFAULT_EQUATIONS_NUMBER = 2; private static final int DEFAULT_VARIABLES_NUMBER = 2; public static void main(String args[]){ LinearSystem<Float, MyEquation> list = generateSystem(); printSystem(list); int i, j; Algorithm<Float, MyEquation> alg = new Algorithm<Float, MyEquation>(list); try{ alg.calculate(); }catch (NullPointerException e){ System.out.println(e.getMessage()); System.exit(0); }catch (ArithmeticException e){ System.out.println(e.getMessage()); System.exit(0); } Float [] x = new Float[DEFAULT_EQUATIONS_NUMBER]; for(i = list.size() - 1; i >= 0; i--) { Float sum = 0.0f; for(j = list.size() - 1; j > i; j--) { sum += list.itemAt(i, j) * x[j]; } x[i] = (list.itemAt(i, list.size()) - sum) / list.itemAt(i, j); } printSystem(list); printVector(x); } public static LinearSystem<Float, MyEquation> generateSystem(){ LinearSystem<Float, MyEquation> list = new LinearSystem<Float, MyEquation>(); int i; for (i = 0; i < DEFAULT_EQUATIONS_NUMBER; i++){ MyEquation eq = new MyEquation(); eq.generate(DEFAULT_VARIABLES_NUMBER + 1); list.push(eq); } return list; } public static void printSystem(LinearSystem<Float, MyEquation> system){ for (int i = 0; i < system.size(); i++){ MyEquation temp = system.get(i); String s = ""; for (int j = 0; j < temp.size(); j++){ s += String.format("%f; %s", system.itemAt(i, j), "\t"); } System.out.println(s); }System.out.println(""); } public static void printVector(Float [] x){ String s = ""; for (int i = 0; i < x.length; i++){ s += String.format("x%d = %f; ", i, x[i]); }System.out.println(s); } } Let's launch this miracle to check the correctness of the work ...

It's all. Sources can be downloaded on github.
Conclusion
The Gauss method is not very amenable to generalized programming (as you can see, the reverse is done separately), but there was a kind of implementation that I hope will help someone better understand the art of using interfaces and generics.
References:
Source: https://habr.com/ru/post/270289/
All Articles