Surfaces and bodies of revolution: using the “virtual potter's wheel” in Wolfram | Alpha

Translation of the Peter Barendse post " Surfaces and Solids of the Revolution: Using Wolfram | Alpha's" Virtual Potter's Wheel " ".
The code given in the article can be downloaded here .
Many thanks to Kirill Guzenko KirillGuzenko for his help in translating and preparing the publication.

---

Even before the advent of 3D printing technology, we had the opportunity to create objects of almost any shape, and the only limitations for humanity were associated only with the accuracy that we can provide. And on the way to overcome these limitations, various devices have been developed that are capable of producing products of very complex shapes; The culmination of this process (before the advent of 3D printers) was the emergence of CNC machines and a large number of degrees of freedom:



Historically, one of the first such devices was, perhaps, the potter's wheel, with the help of which we had the opportunity to create highly accurate axisymmetric products of an arbitrary profile. I still see it as magic, depending on how the potter forms the curve with his own hands; how this curve sets the shape for the whole vase through wheel spin:
')


A simple generalization of the potter's wheel is a lathe. In fact, it is a potter's wheel for wood or metal. Lathes are similar to pottery wheels, but the workpiece is horizontal, and the curve is formed by some sharp cutting tools. The cutting tool can also be attached to a guide with a certain outline, as a result of which it is possible to produce products of the same shape.



The machine and the potter's wheel can produce a certain class of bodies, which are called bodies of revolution. The surface of the body of revolution is the surface of rotation.

From the point of view of mathematics, the surface of revolution is the result of the rotation of some curve defined on a plane, around an axis (the axis must lie on the same plane). The resulting surface of rotation is located in three-dimensional space. The body of rotation is the result of the rotation of some two-dimensional region around the axis.

Surfaces and bodies of revolution are usually studied in the second semester of the course of mathematical analysis - as one of the applications of integration. I remember that this topic seemed to me a very useful educational material, because this is the next most intuitive example of the concept of integration after the area under the graph, in which, however, a single integral is used.

Together with 3D printing and Wolfram Language, students have the opportunity to add a visual representation and design experience to the theory and mathematical intuition that they already have. And, as will be shown later, it is not at all necessary to know something from the programming area or to be able to make calculations in order to use the “virtual potter's wheel” in Wolfram | Alpha! And, obeying the call of the potter's wheel, let's make some cup!

After some study of various functions in Wolfram | Alpha (well, I confess, I used Wolfram Language here to be able to interactively control the shape of the curve) I found an interesting candidate for the role of the curve for our cup - it should make something like a cocktail glass:



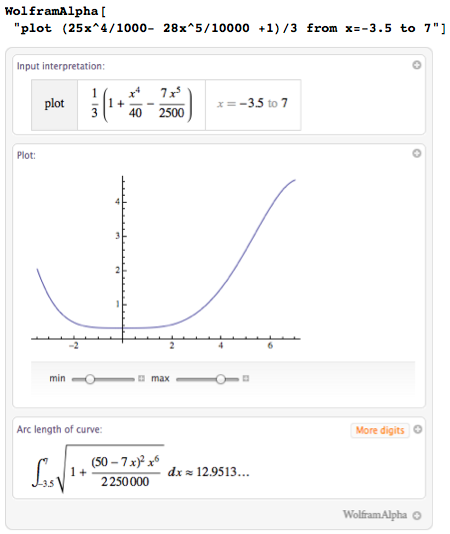
Now I can simply change the plot (build) to revolve (turn), and Wolfram | Alpha will tell me about my glass and show its image:





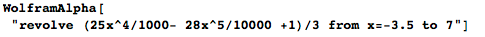
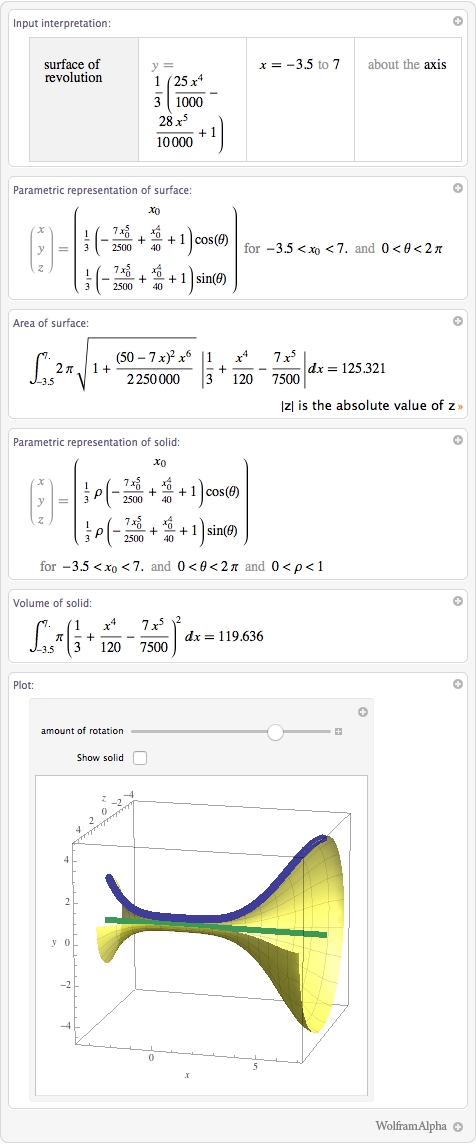
In addition to the equations that define the body and the surface, I get the value of the volume inside the body and the area of ​​its surface. A volume of about 120 - this means that if we used centimeters as a unit of measurement, then my glass will hold 120 ml (120 cc).

However, this volume includes what is contained in the stem of the glass and at its base. A part of this space must be reserved for glass (or another material from which the glass will be made). So let's add an internal curve - I set it by moving the original curve 1/6 down and taking it between 3 and 7:



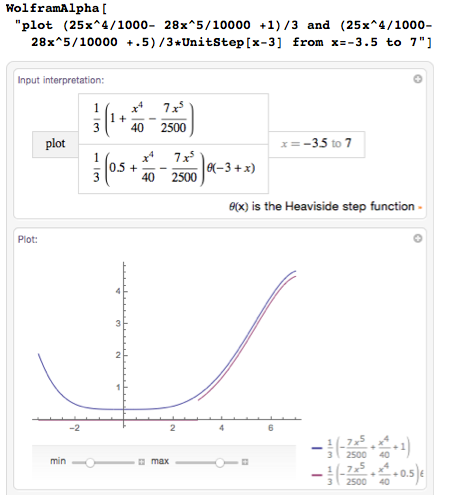
Now I could either print this chart to use it as a template on my lathe (if I had one), or continue working with the “virtual potter's wheel”:





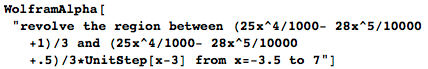
Now I know how much material I need to produce one glass - about 20 cubic cm, that is, we still have about 100 ml of space for drinking in a glass. You can also calculate how much paint we need to spend for staining a glass. Its surface area is approximately 233 cm², and on cans of paint it is usually indicated what painting will be enough for painting.

To print this cup through the Shapeways website, I used the simplified method that Vitaly Kaurov wrote about last year.

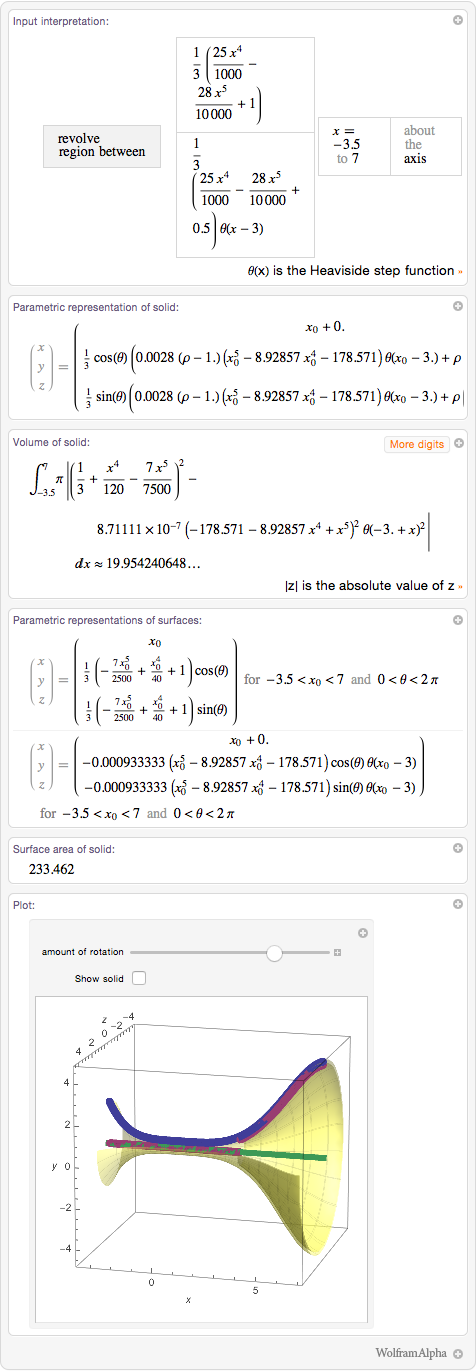
Although I can build any rotation surface in Wolfram Language using RevolutionPlot3D , instead I simply copied the Parametric Surface Representation and used it in ParametricPlot3D (and if you want to implement this through Wolfram | Alpha, then copy the Text Input into Wolfram Language "From the" Parametric Surface Representation "- part of the Wolfram | Alpha output). It turned out that I needed to change something to meet the requirements of Shapeways: first, it was necessary to convert centimeters to millimeters, which I achieved by increasing all dimensions 10 times (using the ScalingTransform ), and secondly I had to set 1.6 mm thickness, which I implemented with PlotStyle :



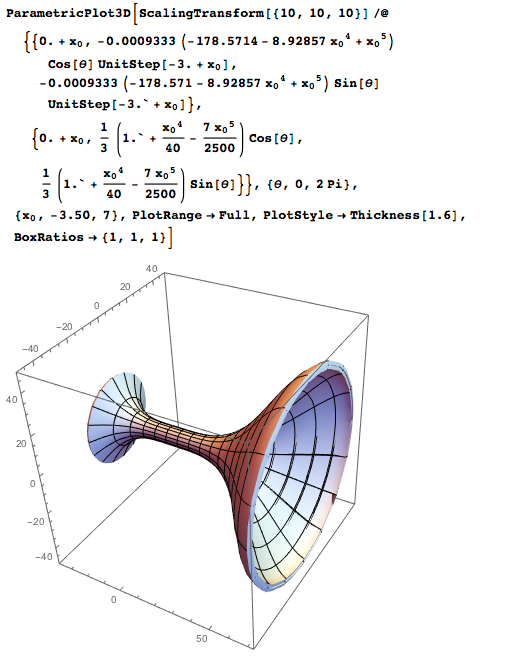
The only thing that was needed after that was to upload the cup in the .stl format on their website:



And ... voila! Here is an image of the finished glass, embodied in plastic (it cost all $ 23):



In Wolfram | Alpha, you can create a wide variety of surfaces and rotation bodies using various functions, axes and rotation parameters:





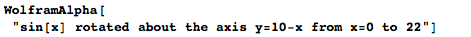
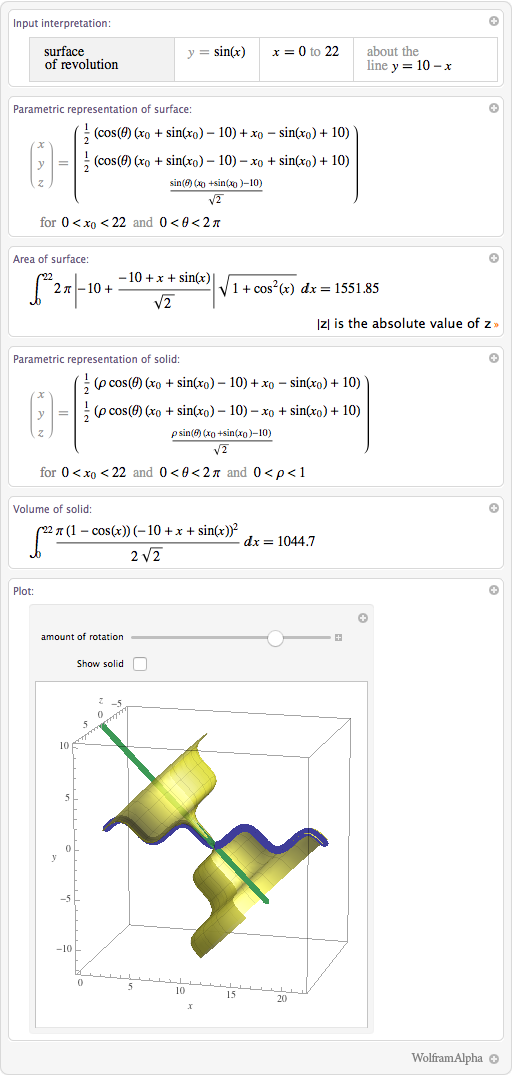
I can even rotate an infinitely long part of the curve, which will lead us to a mathematical “paradox” called the horns of Gabriel (or the Torricelli tube):



Wolfram | Alpha reports that the resulting volume is π, but the surface area is infinite! It seems that it follows from this that I can fill the horn with a finite amount of paint, but this amount should not be enough to cover the entire inner surface - some kind of absurdity is obtained. Of course, the layer of paint is actually not two-dimensional, and at some point the tube narrows so much that no molecule can pass through it anymore, so from the point of view of physics we have no paradox.

Soon, Wolfram | Alpha Pro users will be able to access step-by-step solutions for finding the surface area and volume of rotation, showing how you can calculate individual components of a surface or volume and combine them together. I would be happy to hear from you ideas on how you can still use this technique.

And now, holding this glass in my hands now (partly because I did not take into account his tendency to toppling over), I propose a toast: for creativity and for those tools that allow us to realize our ideas. We will!