Practical application of Fourier transform for signal analysis. Introduction for beginners

1. Fourier transform and signal spectrum

In many cases, the problem of obtaining (calculating) the spectrum of a signal is as follows. There is an A / D converter, which, with a sampling frequency Fd, converts a continuous signal arriving at its input during time T, into digital samples there are N pieces. Next, the array of samples is fed into a program that produces N / 2 of some numerical values ​​(the programmer, who pulled the program from the Internet , says that it does the Fourier transform).

To check whether the program is working correctly, we will form an array of samples as the sum of two sinusoids sin (10 * 2 * pi * x) + 0.5 * sin (5 * 2 * pi * x) and drop the program. The program has drawn the following:


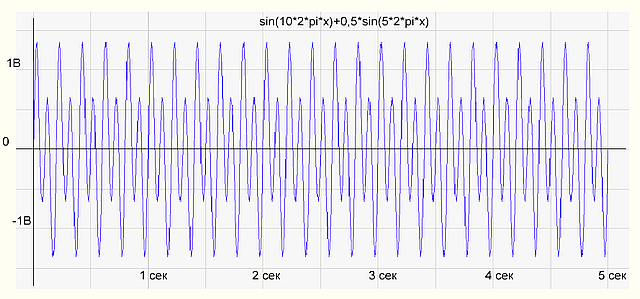
Fig.1 Graph of the time function of the signal
')

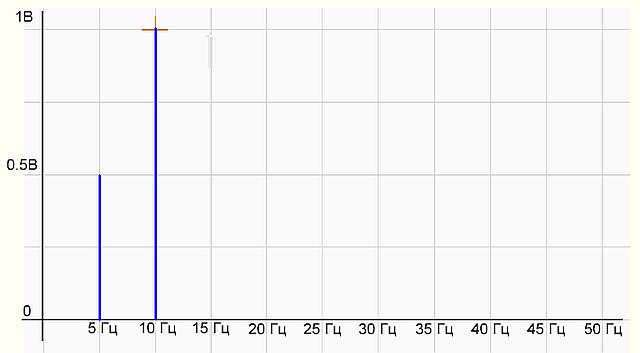
Fig.2 Graph of the signal spectrum

On the spectrum graph there are two sticks (harmonics) of 5 Hz with an amplitude of 0.5 V and 10 Hz - with an amplitude of 1 V, all as in the formula of the original signal. Everything is fine, the programmer is well done! The program works correctly.

This means that if we apply a real signal from a mixture of two sinusoids to the input of the ADC, we will get a similar spectrum consisting of two harmonics.

Total, our real measured signal, with a duration of 5 seconds , digitized by the ADC, that is, represented by discrete readings, has a discrete non-periodic spectrum.

From a mathematical point of view - how many errors in this phrase?

Now the bosses decided we decided that 5 seconds is too long, let's measure the signal in 0.5 seconds.


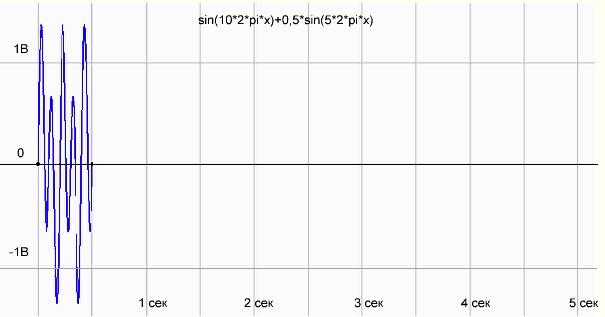
Fig.3 Graph of the function sin (10 * 2 * pi * x) + 0.5 * sin (5 * 2 * pi * x) on the measurement period 0.5 sec


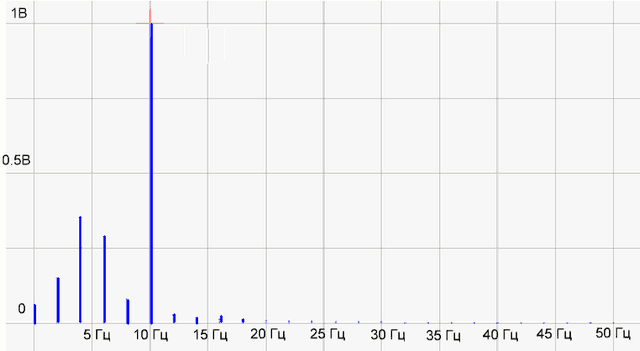
Fig.4 Spectrum function

Something as if not that! The harmonica of 10 Hz is drawn normally, but instead of a stick at 5 Hz, some kind of incomprehensible harmonics appeared. We look on the Internet, that yes how ...

In, they say that you need to add zeros to the end of the sample and the spectrum will be drawn normal.


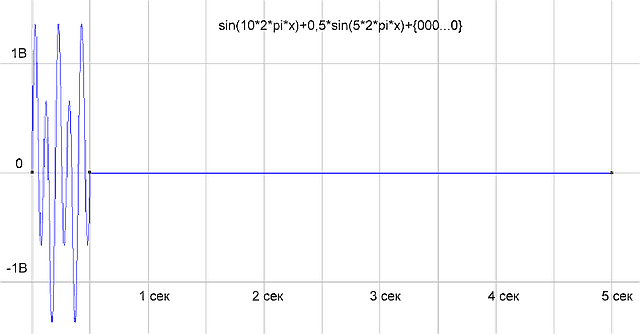
Fig.5 Finish zeros up to 5 seconds


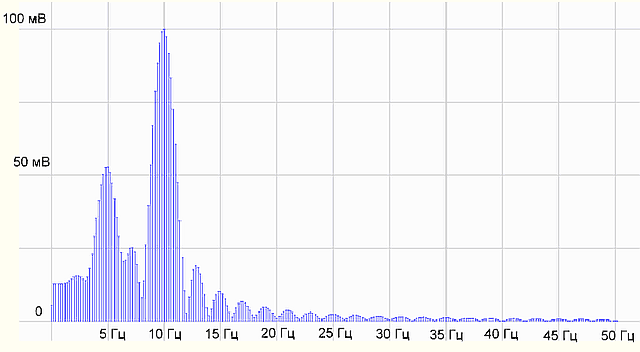
Fig.6 Received spectrum

All the same, not what was 5 seconds. We'll have to deal with the theory. We go to Wikipedia - the source of knowledge.

2. Continuous function and its representation by Fourier series

Mathematically, our signal with a duration of T seconds is some function f (x) defined on the interval {0, T} (X in this case is time). Such a function can always be represented as a sum of harmonic functions (sine waves or cosine curves) of the form:

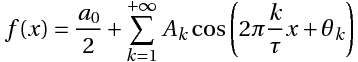(1) where:

k is the number of the trigonometric function (the number of the harmonic component, the number of the harmonic)
T - the segment where the function is defined (signal duration)
Ak is the amplitude of the k-th harmonic component,
θk is the initial phase of the kth harmonic component

What does it mean to “present a function as a sum of a series”? This means that by adding the values ​​of the harmonic components of the Fourier series at each point, we obtain the value of our function at this point.

(More strictly, the standard deviation of the series from the function f (x) will tend to zero, but despite the mean square convergence, the Fourier series of a function, generally speaking, does not have to converge to it point by point. See https://ru.wikipedia.org/ wiki / Row_Fourier .)

This series can also be written in the form:

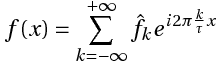(2)
Where 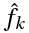, kth complex amplitude.

or

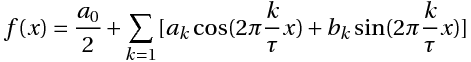(3)

The relationship between the coefficients (1) and (3) is expressed by the following formulas:



and



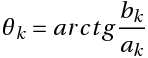
Note that all these three representations of the Fourier series are completely equivalent. Sometimes when working with Fourier series, it is more convenient to use instead of sines and cosines the exponents of an imaginary argument, that is, to use the Fourier transform in a complex form. But it is convenient for us to use the formula (1), where the Fourier series is represented as a sum of cosine curves with the corresponding amplitudes and phases. In any case, it is wrong to say that the result of the Fourier transform of a real signal will be the complex amplitudes of the harmonics. As correctly stated in the Wiki, “Fourier Transform (ℱ) is an operation that associates one function of a real variable with another function, also a real variable.”

Total:
The mathematical basis of the spectral analysis of signals is the Fourier transform.

The Fourier transform allows you to represent a continuous function f (x) (signal) defined on the interval {0, T} as the sum of an infinite number (infinite series) of trigonometric functions (sinusoids and / or cosine waves) with certain amplitudes and phases, also considered on the segment {0, T}. This series is called the Fourier series.

Note some more points, the understanding of which is required for the correct application of the Fourier transform to the analysis of signals. If we consider the Fourier series (the sum of sinusoids) on the whole X axis, then we can see that outside the segment {0, T} the function represented by the Fourier series will periodically repeat our function.

For example, in the graph in Fig. 7, the original function is defined on the segment {-T \ 2, + T \ 2}, and the Fourier series represents a periodic function defined on the entire x axis.

This happens because the sinusoids themselves are periodic functions, respectively, and their sum will be a periodic function.


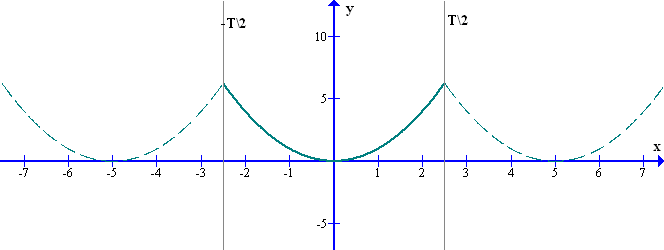
Fig.7 Representation of non-periodic source function near Fourier

In this way:

Our initial function is continuous, non-periodic, defined on some segment of length T.
The spectrum of this function is discrete, that is, presented in the form of an infinite series of harmonic components — the Fourier series.
In fact, some periodic function is determined by the Fourier series, which coincides with ours on the segment {0, T}, but for us this periodicity is not significant.

Further.

The periods of the harmonic components are multiples of the segment {0, T}, on which the initial function f (x) is defined. In other words, the periods of harmonics are multiples of the signal measurement duration. For example, the period of the first harmonic of the Fourier series is equal to the interval T, on which the function f (x) is defined. The period of the second harmonic of the Fourier series is equal to the interval T / 2. And so on (see fig. 8).


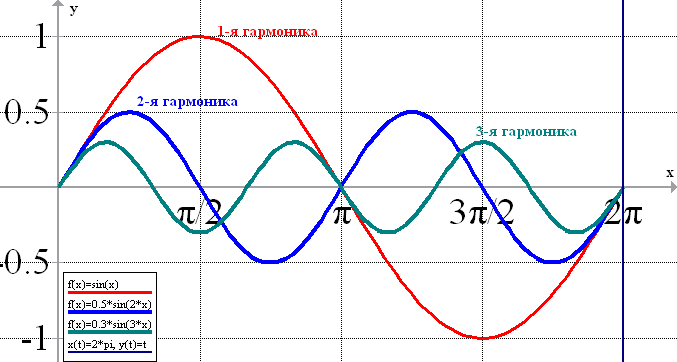
Fig.8 Periods (frequencies) of the harmonic components of the Fourier series (here T = 2π)

Accordingly, the frequencies of the harmonic components are multiples of 1 / T. That is, the frequencies of the harmonic components Fk are equal to Fk = \ T, where k runs through values ​​from 0 to ∞, for example, k = 0 F0 = 0; k = 1 F1 = 1 \ T; k = 2 F2 = 2 \ T; k = 3 F3 = 3 \ T; ... Fk = k \ T (at zero frequency there is a constant component).

Let our original function, is a signal recorded for T = 1 sec. Then the period of the first harmonic will be equal to the duration of our signal T1 = T = 1 sec and the frequency of the harmonic is 1 Hz. The period of the second harmonic will be equal to the duration of the signal divided by 2 (T2 = T / 2 = 0.5 sec) and the frequency is equal to 2 Hz. For the third harmonic T3 = T / 3 sec and the frequency is 3 Hz. And so on.

The pitch between the harmonics in this case is 1 Hz.

Thus, a signal with a duration of 1 s can be decomposed into harmonic components (to obtain a spectrum) with a resolution of 1 Hz.
To increase the resolution by 2 times to 0.5 Hz - it is necessary to increase the measurement time by 2 times - up to 2 seconds. A signal with a duration of 10 seconds can be decomposed into harmonic components (to obtain a spectrum) with a resolution of 0.1 Hz. There are no other ways to increase the frequency resolution.

There is a way to artificially increase the duration of a signal by adding zeros to an array of samples. But it does not increase the actual frequency resolution.

3. Discrete signals and discrete Fourier transform

With the development of digital technology, the ways of storing measurement data (signals) have changed. If before the signal could be recorded on a tape recorder and stored on a tape in analog form, now the signals are digitized and stored in files in the computer's memory as a set of numbers (counts).

The usual scheme of measuring and digitizing the signal is as follows.


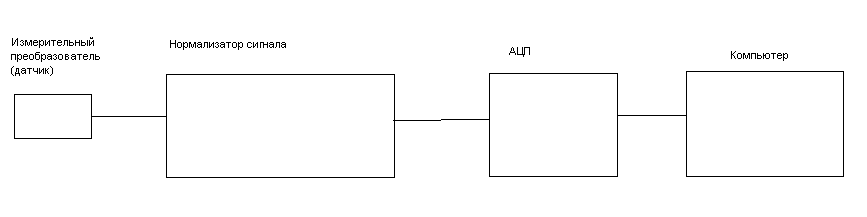
Fig.9 Measuring channel diagram

The signal from the transmitter is fed to the ADC over a period of time T. The signal samples (sampling) obtained at time T are transmitted to a computer and stored in memory.


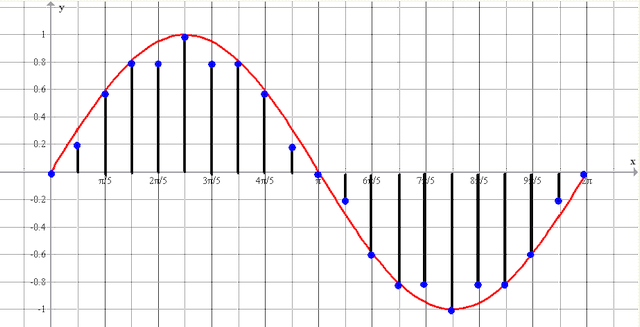
Fig.10 Digitized signal - N samples received during T

What are the requirements for signal digitization parameters? A device that converts an input analog signal to a discrete code (digital signal) is called an analog-to-digital converter (ADC, English Analog-to-digital converter, ADC) (Wiki).

One of the main parameters of the ADC is the maximum sampling frequency (or sampling frequency, English sample rate) - the sampling rate of a continuous signal in time when it is sampled. Measured in hertz. ((Wiki))

According to the Kotelnikov theorem, if a continuous signal has a spectrum limited by the frequency Fmax, then it can be completely and unambiguously reconstructed from its discrete readings taken at time intervals 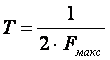i.e. with frequency Fd ≥ 2 * Fmax, where Fd is the sampling frequency; Fmax is the maximum frequency of the signal spectrum. In other words, the signal digitization frequency (ADC sampling frequency) should be at least 2 times higher than the maximum frequency of the signal that we want to measure.

And what will happen if we take the samples with a smaller frequency than that required by the Kotelnikov theorem?

In this case, an “aliasing” effect occurs (aka the stroboscopic effect, the moire effect), in which the high-frequency signal after digitization turns into a low-frequency signal, which actually does not exist. In fig. 11 red high frequency sine wave is a real signal. The blue sinusoid of a lower frequency is a fictitious signal, arising due to the fact that during the time of taking the reference it has time to pass more than a half-period of a high-frequency signal.


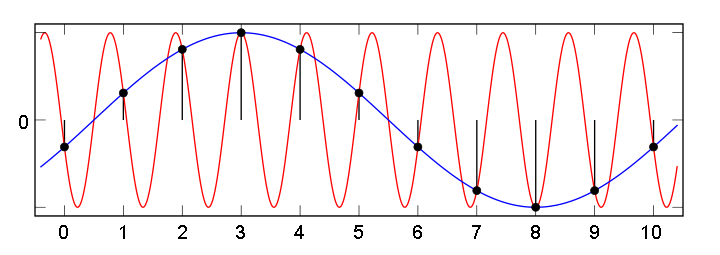
Fig. 11. The appearance of a false low frequency signal at an insufficiently high sampling rate

To avoid the aliasing effect, a special anti-aliasing filter is put in front of the ADC - a low-pass filter (low-pass filter), which passes frequencies lower than half of the ADC sampling frequency, and kills higher frequencies.

In order to calculate the spectrum of the signal from its discrete samples, the discrete Fourier transform (DFT) is used. Note again that the spectrum of a discrete signal "by definition" is limited to the frequency Fmax, less than half the sampling frequency Fd. Therefore, the spectrum of a discrete signal can be represented by a sum of a finite number of harmonics, in contrast to an infinite sum for a Fourier series of a continuous signal, the spectrum of which can be unlimited. According to the Kotelnikov theorem, the maximum harmonic frequency must be such that it has at least two readings, so the number of harmonics is equal to half the number of readings of a discrete signal. That is, if there are N samples in the sample, then the number of harmonics in the spectrum will be N / 2.

We now consider the discrete Fourier transform (DFT).



Comparing with the Fourier series



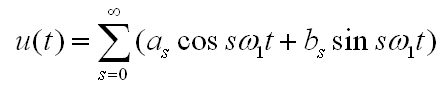
we see that they coincide, except that the time in the DFT is discrete in nature and the number of harmonics is limited to N / 2 - half the number of samples.

The DFT formulas are written in dimensionless integer variables k, s, where k is the number of signal samples, s is the number of spectral components.
The value s shows the number of total harmonic oscillations on the period T (the duration of the signal measurement). The discrete Fourier transform is used to find amplitudes and phases of harmonics by a numerical method, i.e. "on the computer"

Returning to the results obtained at the beginning. As mentioned above, when decomposing a non-periodic function (our signal) into a Fourier series, the resulting Fourier series actually corresponds to a periodic function with a period T. (Fig. 12).


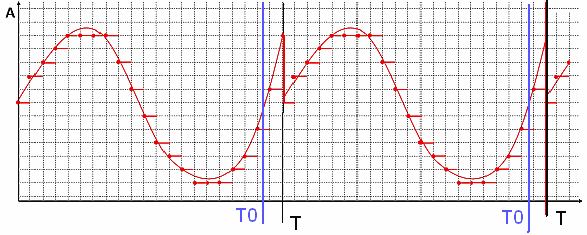
Fig.12 Periodic function f (x) with a period T0, with a measurement period T> T0

As can be seen in Figure 12, the function f (x) is periodic with a period T0. However, due to the fact that the duration of the measuring sample T does not coincide with the period of the function T0, the function obtained as a Fourier series has a discontinuity at the point T. As a result, the spectrum of this function will contain a large number of high-frequency harmonics. If the duration of the measurement sample T coincided with the period of the function T0, then only the first harmonic (a sinusoid with a period equal to the sample duration) would be present in the spectrum obtained after the Fourier transform, since the function f (x) is a sinusoid.

In other words, the DFT program “does not know” that our signal is a “piece of a sine wave”, but tries to present a periodic function in the form of a series, which has a discontinuity due to the inconsistency of individual pieces of the sinusoid.

As a result, harmonics appear in the spectrum, which should summarize the shape of the function, including this discontinuity.

Thus, in order to obtain a “correct” signal spectrum, which is the sum of several sinusoids with different periods, it is necessary that an integer number of periods of each sinusoid fit into the signal measurement period. In practice, this condition can be met with a sufficiently long duration of the signal measurement.


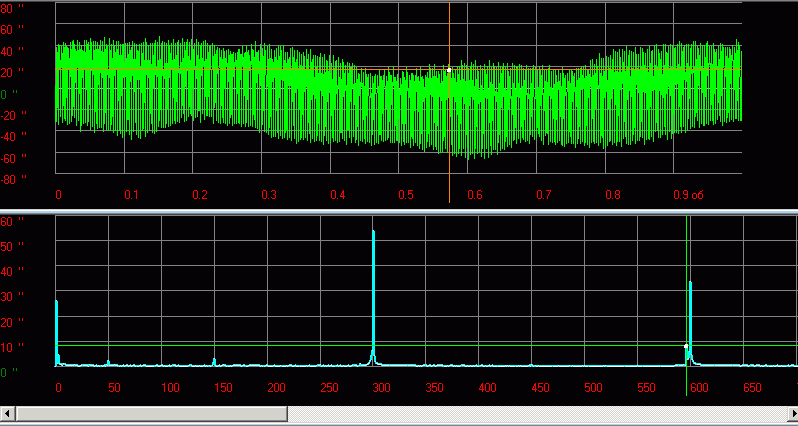
Fig.13 An example of the function and spectrum of the signal kinematic error gear

With a shorter duration, the picture will look “worse”:


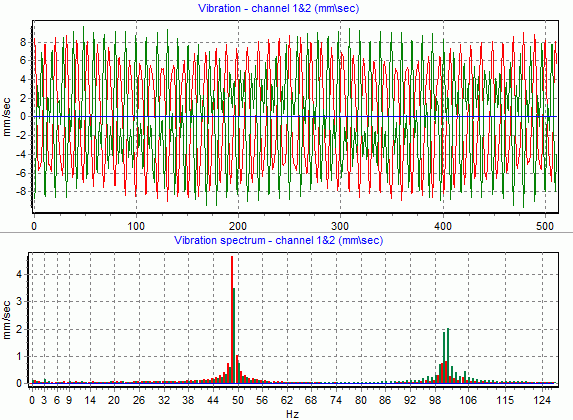
Fig.14 An example of the function and spectrum of the vibration signal of the rotor

In practice, it is difficult to understand where the “real components” and where are the “artifacts” caused by the inconsistency of the periods of the components and the duration of the signal sampling or “jumps and breaks” of the waveform. Of course, the words “real components” and “artifacts” were not quoted in vain. The presence in the spectrum of a spectrum of many harmonics does not mean that our signal in reality “consists of”. It is the same as to assume that the number 7 "consists" of the numbers 3 and 4. The number 7 can be represented as the sum of the numbers 3 and 4 - this is correct.

Similarly, our signal ... or rather, not even “our signal”, but a periodic function compiled by repeating our signal (sampling) can be represented as a sum of harmonics (sinusoids) with certain amplitudes and phases. But in many cases that are important for practice (see the figures above), it is really possible to associate the harmonics obtained in the spectrum and with real processes that are cyclical in nature and make a significant contribution to the waveform.

Some results

1. The real measured signal, with a duration of T s, digitized by the ADC, that is, represented by a set of discrete samples (N pieces), has a discrete non-periodic spectrum represented by a set of harmonics (N / 2 pieces).

2. The signal is represented by a set of real values ​​and its spectrum is represented by a set of real values. The harmonic frequencies are positive. The fact that it is more convenient for mathematicians to present the spectrum in a complex form with the use of negative frequencies does not mean that “this is right” and “this is always the case”.

3. The signal measured at the time interval T is determined only at the time interval T. What happened before we started measuring the signal and what happens after that - science does not know. And in our case - uninteresting. The DFT of a time-limited signal gives its “real” spectrum, in the sense that, under certain conditions, it makes it possible to calculate the amplitude and frequency of its components.

Used materials and other useful materials.

FourierScope is a program for building radio signals and their spectral analysis.
Graph is an open source program designed to build mathematical graphs.
DISCRETE FOURIER TRANSFORMATION - HOW IT DOES IT
Discrete Fourier Transform (DFT)