Algorithm of search of object displacement in the image
In the last article I described a simple algorithm for recognizing moving objects in a dynamic picture. And now I will describe a slightly different situation. Suppose we already have the coordinates of the object and we need to determine in which direction it has shifted. By coordinates, I mean the coordinates of a conditional point on an object, for simplicity, assuming that the object does not change its orientation in space. The fact that the object itself has shifted can be determined by subtracting a specific area of the frame from the area of another frame. In the last article I did just that, just for the whole frame.
It may be tempting to solve this problem "head on" by going through the whole picture. However, such an operation may be too time consuming. Some other algorithm suggests itself.
So, a small experiment, the same pictures, I assume that the car was moving in a straight line. I take an area of 25 by 25 pixels in size, shift it along the intended trajectory of the vehicle and calculate the total deviation of pixel brightness, here's the program code:
See the resulting graph:
')
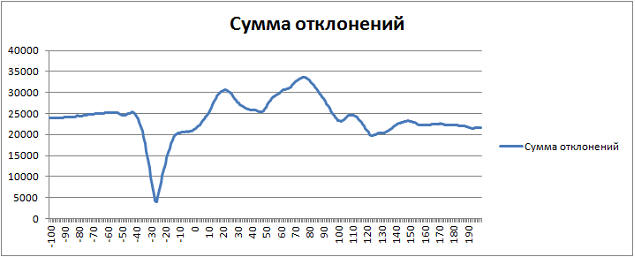
What do we get? At some point, this sum of deviations is minimal, but not zero. Why not zero? Perhaps the direction of the car was not quite straight, it could also be various noises (for example, raindrops, hand tremors, and so on). To test this hypothesis, I nevertheless conducted an experiment with a head-on search, by sorting the coordinates over a large area of the picture. It turned out my assumption was true, the car really moved in a straight line, since the smallest value of the objective function turned out to be exactly at zero displacement along the y axis, that is, only horizontally moving. It remains to write off all the noises. Although, it would not hurt to look at the frame subtraction mask at the point found:

In the field of subtraction, the edges of the headlights are visible, apparently, just some kind of glare.
The question arises: is it possible to apply something like descending a gradient or finding a minimum of an objective function to search for a new position of an object? If you look closely at the graph, we see that the function has quite a few local extremes, and it is not yet clear how to make the algorithm not confuse the local extremum with the main one.
There is such an idea: what if we use a binary search? We first take the function along the x axis, then along y, find the quadrant where the function is minimal, divide it into four such quadrants, and so on until we find the desired point. This is much faster than bypassing all points of the search area.
For the experiment, another picture was chosen: an ellipse, shifting simultaneously both horizontally and diagonally:
Build a graph of the objective function on the x axis:
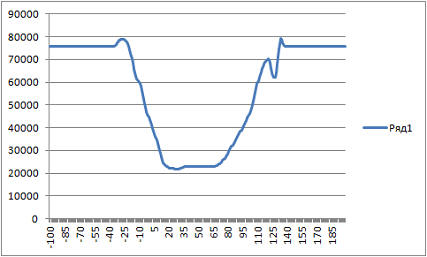
Extremum of the function when dx = 24
And on the y axis:
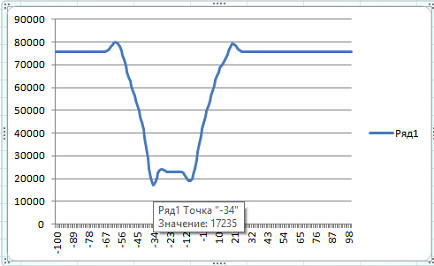
Extremum at -34.
As we see. on the dy axis, the extremum was found correctly, and in x - we found that the object is displaced in a completely different quadrant, the extremum in the region dx> 0, although in fact the displacement was in the direction of decreasing x. So, we need some other algorithm.
You can try to hold a perpendicular line through the extremum point and look for an extremum along it. And then through a point to an extremum on the same straight line, draw a perpendicular line. Thus, we have a straight line on which we are looking for an extremum, which will then be parallel to the axis Ox, then Oy. So, try, find the extremum at Ox, look for an axis parallel to Oy with dx = 24:
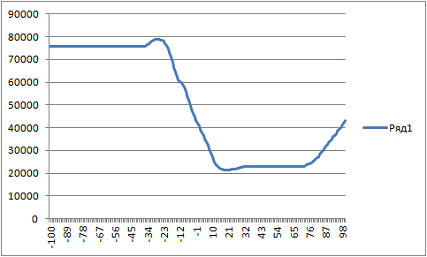
Extremum with dy = -1. Draw a line through the point dx = 24, dy = -1, parallel to the axis Ox. we get the following result:

Now we have an extremum already at the point dx = 18. Already a little closer to the truth. The only question is: will the extremum be found in this way and how much more effectively will it be than by a “blunt brute force”?
So, first blunt bust. The algorithm found an extremum at the point dx = -12, dy = -23 for 15556 iterations:
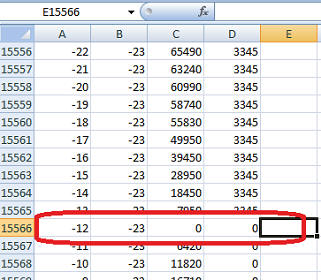
The total number of iterations in this example is 40401. The execution time on my laptop is approximately 0.7 seconds. For processing streaming video, this speed is, of course, unacceptable.
Now we will try to implement the above idea with a gradual approximation:
This algorithm found the offset for 12600 iterations (63 to 200):
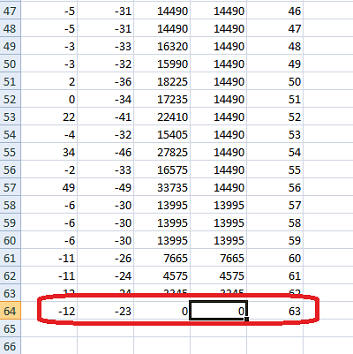
It is somewhat faster. True, the algorithm itself is not the most optimal, it can be further optimized. Another disadvantage is that if you choose the wrong starting points, it will freeze and find nothing. For example, I first chose -100, -100, and the search did not work.
If this topic is interesting to you, then I will discuss how to further improve this algorithm and eliminate its drawbacks, as well as how to work with it on real, rather than hand-drawn, pictures.
It may be tempting to solve this problem "head on" by going through the whole picture. However, such an operation may be too time consuming. Some other algorithm suggests itself.
So, a small experiment, the same pictures, I assume that the car was moving in a straight line. I take an area of 25 by 25 pixels in size, shift it along the intended trajectory of the vehicle and calculate the total deviation of pixel brightness, here's the program code:
private void tsmiFindShift_Click(object sender, EventArgs e) { ImageMatrix matrix1 = create_matrix("D:\\3\\1.png"); ImageMatrix matrix2 = create_matrix("D:\\3\\2.png"); Bitmap picture = new Bitmap(matrix1.picture); using (var wrapper = new ImageWrapper(picture, true)) { int x1 = 110; int x2 = x1+25; int y1 = 140; int y2 = y1+25; int dx = 0; int dy = 0; StringBuilder sb = new StringBuilder(); for (dx = -100; dx < 200; dx++) { Int64 res = 0; for (int i = x1; i < x2; i++) { for (int j = y1; j < y2; j++) { int light1 = matrix1.matrix[i, j]; int light2 = matrix2.matrix[i + dx, j + dy]; int light = Math.Abs(light2 - light1); res = res + light; } } sb.AppendFormat("{0}; {1};\n", res, dx); } System.IO.File.WriteAllText("D:\\3\\1.txt", sb.ToString()); pbImage.Image = picture; } See the resulting graph:
')

What do we get? At some point, this sum of deviations is minimal, but not zero. Why not zero? Perhaps the direction of the car was not quite straight, it could also be various noises (for example, raindrops, hand tremors, and so on). To test this hypothesis, I nevertheless conducted an experiment with a head-on search, by sorting the coordinates over a large area of the picture. It turned out my assumption was true, the car really moved in a straight line, since the smallest value of the objective function turned out to be exactly at zero displacement along the y axis, that is, only horizontally moving. It remains to write off all the noises. Although, it would not hurt to look at the frame subtraction mask at the point found:

In the field of subtraction, the edges of the headlights are visible, apparently, just some kind of glare.
The question arises: is it possible to apply something like descending a gradient or finding a minimum of an objective function to search for a new position of an object? If you look closely at the graph, we see that the function has quite a few local extremes, and it is not yet clear how to make the algorithm not confuse the local extremum with the main one.
There is such an idea: what if we use a binary search? We first take the function along the x axis, then along y, find the quadrant where the function is minimal, divide it into four such quadrants, and so on until we find the desired point. This is much faster than bypassing all points of the search area.
For the experiment, another picture was chosen: an ellipse, shifting simultaneously both horizontally and diagonally:

Build a graph of the objective function on the x axis:

Extremum of the function when dx = 24
And on the y axis:

Extremum at -34.
As we see. on the dy axis, the extremum was found correctly, and in x - we found that the object is displaced in a completely different quadrant, the extremum in the region dx> 0, although in fact the displacement was in the direction of decreasing x. So, we need some other algorithm.
You can try to hold a perpendicular line through the extremum point and look for an extremum along it. And then through a point to an extremum on the same straight line, draw a perpendicular line. Thus, we have a straight line on which we are looking for an extremum, which will then be parallel to the axis Ox, then Oy. So, try, find the extremum at Ox, look for an axis parallel to Oy with dx = 24:

Extremum with dy = -1. Draw a line through the point dx = 24, dy = -1, parallel to the axis Ox. we get the following result:

Now we have an extremum already at the point dx = 18. Already a little closer to the truth. The only question is: will the extremum be found in this way and how much more effectively will it be than by a “blunt brute force”?
So, first blunt bust. The algorithm found an extremum at the point dx = -12, dy = -23 for 15556 iterations:

The total number of iterations in this example is 40401. The execution time on my laptop is approximately 0.7 seconds. For processing streaming video, this speed is, of course, unacceptable.
Now we will try to implement the above idea with a gradual approximation:
private ResStruct search(ImageMatrix matrix1, ImageMatrix matrix2, int x1, int y1, int x2, int y2, StringBuilder sb, int x_beg, int y_beg, int x_end, int y_end) { Int64 min_res = 999999999999999999; ResStruct result = new ResStruct(); int min_dx = 999999999; int min_dy = 999999999; for (int dy = y_beg; dy <= y_end; dy++) { for (int dx = x_beg; dx <= x_end; dx++) { Int64 res = 0; for (int i = x1; i < x2; i++) { for (int j = y1; j < y2; j++) { int light1 = matrix1.matrix[i, j]; int light2 = matrix2.matrix[i + dx, j + dy]; int light = Math.Abs(light2 - light1); res = res + light; } } if (res < min_res) { min_res = res; min_dx=dx; min_dy=dy; } //sb.AppendFormat("{0}; {1}; {2}; {3};\n", dx, dy, res, min_res); } } result.dx = min_dx; result.dy = min_dy; result.res = min_res; return result; } private void tsmiFastFindShift_Click(object sender, EventArgs e) { ImageMatrix matrix1 = create_matrix("D:\\3\\11.png"); ImageMatrix matrix2 = create_matrix("D:\\3\\12.png"); Bitmap picture = new Bitmap(matrix1.picture); using (var wrapper = new ImageWrapper(picture, true)) { int x1 = 140; int x2 = x1 + 25; int y1 = 110; int y2 = y1 + 25; Random rnd=new Random(); StringBuilder sb = new StringBuilder(); DateTime dt1 = DateTime.Now; Int64 min_res = 999999999999999999; int min_dx = 0; int min_dy = 0; int k=0; bool flag = false; do { ResStruct res; if (flag) { res = search(matrix1, matrix2, x1, y1, x2, y2, sb, min_dx, -100, min_dx, 100); } else { res = search(matrix1, matrix2, x1, y1, x2, y2, sb, -100, min_dy, 100, min_dy); } flag = !flag; if (res.res < min_res) { min_res = res.res; min_dx = res.dx; min_dy = res.dy; } else { // ( ) // if (flag) min_dy = min_dy + rnd.Next(10) - 5; else min_dx=min_dx + rnd.Next(10) - 5; } sb.AppendFormat("{0}; {1}; {2}; {3}; {4}\n", res.dx, res.dy, res.res, min_res, k); k++; } while (k < 1000 && min_res>=1); DateTime dt2 = DateTime.Now; MessageBox.Show(dt1.ToString() + " " + dt2.ToString()); System.IO.File.WriteAllText("D:\\3\\1.txt", sb.ToString()); for (int i = x1; i < x2; i++) { for (int j = y1; j < y2; j++) { int light1 = matrix1.matrix[i, j]; int light2 = matrix2.matrix[i + min_dx, j + min_dy]; int light = Math.Abs(light2 - light1); wrapper[i, j] = Color.FromArgb(light, light, light); } } pbImage.Image = picture; } } This algorithm found the offset for 12600 iterations (63 to 200):

It is somewhat faster. True, the algorithm itself is not the most optimal, it can be further optimized. Another disadvantage is that if you choose the wrong starting points, it will freeze and find nothing. For example, I first chose -100, -100, and the search did not work.
If this topic is interesting to you, then I will discuss how to further improve this algorithm and eliminate its drawbacks, as well as how to work with it on real, rather than hand-drawn, pictures.
Source: https://habr.com/ru/post/269685/
All Articles