I2P: Transparent EdDSA Signature Implementation
Recently, the electronic signature Ed25519, based on the type of elliptic curve proposed by Bernstein, is gaining increasing popularity. As the number of I2P nodes with this type of signature increased, it became necessary to support it in its I2P implementation, since Ed25519 is not part of popular cryptographic libraries. As a rule, varieties of ref10 from the SUPERCOP library, implemented by Bernstein himself in assembler, and then ported to other languages, are used. This implementation works well and quickly, but it has a major drawback - it is incomprehensible. Indeed, if you look at the source code, you can see a large number of lines of the same type operating with many “magic” numbers, and it’s impossible to understand what they mean without going into theory. The purpose of this article is a mathematically transparent implementation of Ed22519, using only standard operations with large numbers that are present in any cryptographic library, at a speed sufficient for practical use in I2P.
An implicit equation of a flat curve of a special type, called an elliptic curve, is given. Sets a prime number that forms a modulo residue field. The coordinates of the points of the curve belong to this field, i.e. are non-negative integer numbers not exceeding the modulus. Above the two points of the curve, the addition operation is defined so that the new point also belongs to the curve. If we add the point to itself, we get multiplication by 2, if we add it again, then by 3, and so on, multiplication by an arbitrary number n. Also together with the curve is set the base point belonging to the curve, operations on which are used in cryptography.
For cryptography, an arbitrary large number n is selected, which is the secret key, the base point is multiplied by it and the new point serves as a public key, which is then multiplied by the opposite side to another number in order to agree on the key or verify the signature. Persistence is based on the current lack of a known method for determining a multiplier by a point in a reasonable time.
Bershtein proposed to use an elliptic curve with the following parameters.
Curve equation:
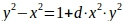 where
where 
Module:
q =
hence the name of the curve.
')
Base point :
(x, 4/5), where x is obtained by solving the equation (see below)
Its coordinates are explicitly:
x = 15112221349535400772501151409588531511454012693041857206046113283949847762202,
y = 46316835694926478169428394003475163141307993866256225615783033603165251855960.
Addition:
 where
where 
It should be noted that division here is not an ordinary division with a remainder, but multiplication by an inverse modulo element, calculated according to Fermat’s small theorem using the formula i.e. the operation of exponentiation modulo.
i.e. the operation of exponentiation modulo.
As a public key, it is proposed to use only the y coordinate, if necessary, solve the equations of the curve with respect to x, and calculate it using the formula .
.
Since q is representable as 8 * k + 5 , to calculate the square root of x , use the formula . Indeed q =
. Indeed q =  =
=  , hence the square root
, hence the square root  .
.
The code is completely located at the address in the Signature.cpp file. To work with large numbers, the BN library functions from openssl are used.
Create the class Ed25519, which implements the curve itself, and contains the curve parameters calculated in its constructor. First of all, 3 methods are needed: addition, multiplication by a number and calculation of x for a given y.
Due to private use, the operation of addition and the laboriousness of the operation of division, we bring x and y to a common denominator (1 + m) * (1-m), thereby getting rid of one division. As a result, the code for addition looks like this:
Also for doubling (adding a point with itself) a separate method Double is implemented, since in this case p1.x = p2.x and p1.y = p2.y, which allows reducing the number of multiplications. In addition, faster BN_sqr is used instead of BN_mul.
Multiplication is released by the simplest method of doubling and adding , i.e. go along the number of bits from senior to junior, at each step double the value of the result, and if the bit is one, then add the multiplying point.
Calculating x over y is trivial.
First, a radical expression:
Then, the square root is calculated using the formula
This topic is quite interesting and extensive, because this issue will be devoted to a separate article . At the same time, the Sign and Verify methods are implemented and used in practice. Therefore, anyone interested, you can look at the code. Some features will be listed here.
Like other electronic signature systems, the EdDSA signature is a pair of 32-byte numbers (R, S), because the signature length is 64 bytes.
Numbers are represented in Little Endian.
SHA-512 is used as a hash function.
When signing, a random number is not generated; instead, the right half of the SHA-512 hash from the secret key, combined with the data being signed, is used.
Also a prime number is used.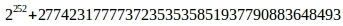 used to select a base point, so that multiplying the base point with it gives zero.
used to select a base point, so that multiplying the base point with it gives zero.
Obviously, the slowest point of this implementation is the division in the operation of addition. In fact, using modern advances in number theory and the specifics of the parameters of EdDSA, you can eliminate it completely, as is done in ref10. However, this will significantly complicate the implementation and make it less understandable, therefore, this should be addressed only if a real practical necessity arises. Currently, EdDSA signature verification in I2P is a rather rare event compared to, say, El-Gamal encryption.
It is believed that the implementation of their own cryptography is a very bad idea. However, the use of unclear how a working implementation seems a little better. In addition, this article may be useful to those who are interested to get to the bottom of it, and working practical code will help with this.
The principle of operation of elliptical cryptography
An implicit equation of a flat curve of a special type, called an elliptic curve, is given. Sets a prime number that forms a modulo residue field. The coordinates of the points of the curve belong to this field, i.e. are non-negative integer numbers not exceeding the modulus. Above the two points of the curve, the addition operation is defined so that the new point also belongs to the curve. If we add the point to itself, we get multiplication by 2, if we add it again, then by 3, and so on, multiplication by an arbitrary number n. Also together with the curve is set the base point belonging to the curve, operations on which are used in cryptography.
For cryptography, an arbitrary large number n is selected, which is the secret key, the base point is multiplied by it and the new point serves as a public key, which is then multiplied by the opposite side to another number in order to agree on the key or verify the signature. Persistence is based on the current lack of a known method for determining a multiplier by a point in a reasonable time.
Ed25519
Bershtein proposed to use an elliptic curve with the following parameters.
Curve equation:
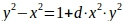 where
where 
Module:
q =

hence the name of the curve.
')
Base point :
(x, 4/5), where x is obtained by solving the equation (see below)
Its coordinates are explicitly:
x = 15112221349535400772501151409588531511454012693041857206046113283949847762202,
y = 46316835694926478169428394003475163141307993866256225615783033603165251855960.
Addition:
 where
where 
It should be noted that division here is not an ordinary division with a remainder, but multiplication by an inverse modulo element, calculated according to Fermat’s small theorem using the formula
 i.e. the operation of exponentiation modulo.
i.e. the operation of exponentiation modulo.As a public key, it is proposed to use only the y coordinate, if necessary, solve the equations of the curve with respect to x, and calculate it using the formula
 .
.Since q is representable as 8 * k + 5 , to calculate the square root of x , use the formula
 . Indeed q =
. Indeed q =  =
=  , hence the square root
, hence the square root  .
.Implementation
The code is completely located at the address in the Signature.cpp file. To work with large numbers, the BN library functions from openssl are used.
Create the class Ed25519, which implements the curve itself, and contains the curve parameters calculated in its constructor. First of all, 3 methods are needed: addition, multiplication by a number and calculation of x for a given y.
class Ed25519 { //... EDDSAPoint Sum (const EDDSAPoint& p1, const EDDSAPoint& p2) const EDDSAPoint Mul (const EDDSAPoint& p, const BIGNUM * e) const BIGNUM * RecoverX (const BIGNUM * y) const //... } Due to private use, the operation of addition and the laboriousness of the operation of division, we bring x and y to a common denominator (1 + m) * (1-m), thereby getting rid of one division. As a result, the code for addition looks like this:
// m = d*p1.x*p2.x*p1.y*p2.y BN_mul (xx, p1.x, p2.x, m_Ctx); //p1.x*p2.x BN_mul (yy, p1.y, p2.y, m_Ctx); //p1.y*p2.y BIGNUM * m = BN_dup (d); BN_mul (m, m, xx, m_Ctx); BN_mul (m, m, yy, m_Ctx); // x = (p1.x*p2.y + p2.x*p1.y)*inv(1 + m) // y = (p1.y*p2.y + p1.x*p2.x)*inv(1 - m) // m1 = 1-m BN_one (m1); BN_sub (m1, m1, m); // m = m+1 BN_add_word (m, 1); // y = (p1.y*p2.y + p1.x*p2.x)*m BN_add (y, xx, yy); BN_mod_mul (y, y, m, q, m_Ctx); // x = (p1.x*p2.y + p2.x*p1.y)*m1 BN_mul (yy, p1.x, p2.y, m_Ctx); BN_mul (xx, p2.x, p1.y, m_Ctx); BN_add (x, xx, yy); // denominator m = m*m1 BN_mod_mul (m, m, m1, q, m_Ctx); Inv (m); BN_mod_mul (x, x, m, q, m_Ctx); // x = x/m BN_mod_mul (y, y, m, q, m_Ctx); // y = y/m Also for doubling (adding a point with itself) a separate method Double is implemented, since in this case p1.x = p2.x and p1.y = p2.y, which allows reducing the number of multiplications. In addition, faster BN_sqr is used instead of BN_mul.
Multiplication is released by the simplest method of doubling and adding , i.e. go along the number of bits from senior to junior, at each step double the value of the result, and if the bit is one, then add the multiplying point.
EDDSAPoint res {zero, one}; if (!BN_is_zero (e)) { int bitCount = BN_num_bits (e); for (int i = bitCount - 1; i >= 0; i--) { res = Double (res); if (BN_is_bit_set (e, i)) res = Sum (res, p); } } Calculating x over y is trivial.
First, a radical expression:
BN_sqr (y2, y, m_Ctx); // y^2 // xx = (y^2 -1)*inv(d*y^2 +1) BN_mul (xx, d, y2, m_Ctx); BN_add_word (xx, 1); Inv (xx); BN_sub_word (y2, 1); BN_mul (xx, y2, xx, m_Ctx); Then, the square root is calculated using the formula

// x = srqt(xx) = xx^(2^252-2) BN_mod_exp (x, xx, two_252_2, q, m_Ctx); Signature and signature verification
This topic is quite interesting and extensive, because this issue will be devoted to a separate article . At the same time, the Sign and Verify methods are implemented and used in practice. Therefore, anyone interested, you can look at the code. Some features will be listed here.
Like other electronic signature systems, the EdDSA signature is a pair of 32-byte numbers (R, S), because the signature length is 64 bytes.
Numbers are represented in Little Endian.
SHA-512 is used as a hash function.
When signing, a random number is not generated; instead, the right half of the SHA-512 hash from the secret key, combined with the data being signed, is used.
Also a prime number is used.
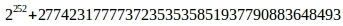 used to select a base point, so that multiplying the base point with it gives zero.
used to select a base point, so that multiplying the base point with it gives zero.Conclusion
Obviously, the slowest point of this implementation is the division in the operation of addition. In fact, using modern advances in number theory and the specifics of the parameters of EdDSA, you can eliminate it completely, as is done in ref10. However, this will significantly complicate the implementation and make it less understandable, therefore, this should be addressed only if a real practical necessity arises. Currently, EdDSA signature verification in I2P is a rather rare event compared to, say, El-Gamal encryption.
It is believed that the implementation of their own cryptography is a very bad idea. However, the use of unclear how a working implementation seems a little better. In addition, this article may be useful to those who are interested to get to the bottom of it, and working practical code will help with this.
Source: https://habr.com/ru/post/269579/
All Articles