Cryptanalysis "Enigma"

All specialists unanimously agreed to read.
Admiral Kurt Fricke, Chief of Naval War Command
Enigma is a rotary ciphering machine used by Nazi Germany during the Second World War. Thanks to the influence exerted on the course of the war, the breaking of the Enigma was perhaps the highlight of the centuries-old history of cryptanalysis. In this topic, I would like to talk about the hacking method used in Bletchley Park, as well as describe the device of the machine itself.
Rotary machines
For the first time cryptographic rotary machines began to be used in the early 20th century. The main component of such devices is a disk (aka the rotor) with 26 electrical contacts on both sides of the disk. Each contact corresponded to the letter of the English alphabet. The contact connection of the left and right sides implemented a simple replacement cipher. When the disk was rotated, the contacts shifted, thereby changing the substitution for each letter. One disc provided 26 different substitutions. This means that when encrypting the same character, the resulting sequence begins to repeat after 26 steps.
To increase the sequence period, you can use several rotors connected in series. When making a full turn of one of the disks, the next disk moves one position. This increases the length of the sequence to 26 n , where n is the number of rotors connected in series.
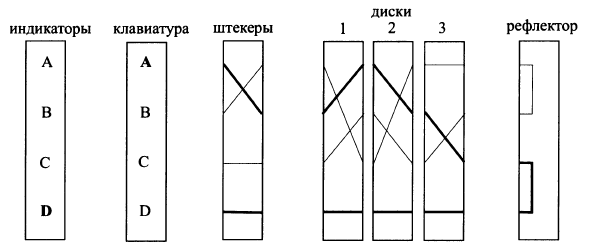
As an example, consider the following image of a simplified rotary machine:

The given machine consists of a keyboard (for entering a character), three disks, an indicator (for displaying a cryptotext) and implements 4 characters encryption: A, B, C, D. In the initial position, the first disk implements a substitution: AC; BA; CB; DD The substitutions of the second and third disks are equal to AB; BC; CA; DD and AA; BC; CB; DD, respectively.
When you press the letter B on the keyboard closes the electrical circuit, depending on the current position of the rotors, and the light on the indicator lights up. In the example above, the letter B will be encrypted in C. Then the first rotor will move one position and the machine settings will take the following form:

Enigma
Enigma is the most popular representative of the world of cryptographic rotary machines. It was used by German troops during the Second World War and was considered practically unbreakable.
The Enigma encryption procedure is implemented as in the example above, with the exception of some additional strokes.
First, the number of rotors in different versions of the Enigma could be different. The most common was the Enigma with three rotors, but the four-disk version was also used.
Secondly, the decryption process of the demo rotary machine described above is different from the encryption process. Each time, for decryption, the left and right rotor will have to be replaced in places, which may not be very convenient. To solve this problem, another disk was added to the Enigma, called a reflector. In the reflector, all contacts were connected in pairs, thereby realizing the repeated passage of the signal through the rotors, but by a different route. Unlike the other rotors, the reflector was always in a fixed position and did not rotate.

Add a replacement reflector (AB; CD) to our demo encryption machine. When you press the key B, the signal passes through the rotors and enters the reflector through the contact C. Here the signal "reflects" and returns, passing through the rotors in the reverse order and in a different way. As a result, the letter B on the output is converted to D.
Note that if you press the D key, the signal will go along the same circuit, converting D to B. Thus, the presence of a reflector made the encryption and decryption processes identical.
Another property of the Enigma associated with the reflector is the impossibility of encrypting any letter in itself. This property has played a very important role in hacking Enigma.
')
The resulting device is already very similar to the real Enigma. With one minor caveat. The resistance of such a machine rests on the secrecy of the internal switching of the rotors. If the device rotors will be disclosed, then hacking is reduced to the selection of their initial positions.
Since each rotor can be in one of 26 positions, for three rotors we get 26 3 = 17476 variants. At the same time, the rotors themselves can also be arranged in an arbitrary order, which increases the difficulty by 3! time. Those. the key space of such a machine will be 6 * 17576 = 105456. This is clearly not enough to ensure a high level of security. Therefore, the Enigma was equipped with another additional tool: a patch panel . Connecting letters on the patch panel in pairs could add one more additional step to encryption.
For example, suppose that the letter B is connected to the letter A on the switching panel. Now when you press A, AB is first substituted, and the letter B is fed to the input of the first rotor
Similarly, the message is decrypted. When the D key is pressed, the rotors and the reflector convert the DDDDCBAB. After which the patch panel converts B to A.
Enigma Resistance Analysis
The real Enigma was different from the one described in the demonstration machine. Namely, the device rotors. In our example, the rotor changes its position only when a full turn is made by the previous disc. In the present Enigma, each disc had a special notch that, in a certain position, hooked the next rotor and shifted it by one position.
The location of the groove for each of the rotors could be adjusted using special external rings. The initial position of the rings did not affect the switching of the rotors and the result of encrypting a single letter, so the rings are not taken into account when calculating the key space of the Enigma.
So, the base model of the Enigma had 3 different rotors, numbered in roman numerals I, II, III and implementing the following substitutions:
Entry = ABCDEFGHIJKLMNOPQRSTUVWXYZ
I = EKMFLGDQVZNTOWYHXUSPAIBRCJ
II = AJDKSIRUXBLHWTMCQGZNPYFVOE
III = BDFHJLCPRTXVZNYEIWGAKMUSQO
When encrypting, the rotors could be arranged in any sequence, which for 6 rotors gives 6 different combinations.
In addition, each rotor could be installed in one of the 26 possible starting positions. Those. the initial position of the rotors has a total
6 * 26 3 = 105456 combinations.
The number of all possible connections on the switching panel is calculated by the formula n! / ((n-2m)! m! 2 m ), where n is the number of letters of the alphabet, m is the number of connected pairs.
For 26 letters of the English alphabet and 10 pairs, this is 150738274937250 = 2 47 different combinations.
Thus, the basic version of the Enigma with three rotors had a solid key space even by modern standards:
150738274937250 * 105456 = 15.896,255,521,782,636,000≈2 64 .
Such a huge number of options inspired a deceptive feeling of invulnerability.
Enigma Cryptanalysis
A large key space provides the Enigma cipher with a rather serious level of resistance to attacks using a well-known ciphertext.
A complete search of 2 64 options, even on modern computers, is not a simple matter.
However, everything changes if you apply the attack with known plaintext. For such a case, there is a very clever method that allows you to neglect the settings of the switching panel in the process of searching for a key combination, which reduces the key space of the Enigma to only 105,456 combinations and makes the entire cipher fatally vulnerable.
The method exploits the presence of a pair of open-closed text of the so-called "cycles". To explain the concept of "cycle", consider the following open message P and its corresponding cryptotext C, encoded by the Enigma.
P = WETTERVORHERSAGEBISKAYA
C = RWIVTYRESXBFOGKUHQBAISE
We write each symbol of the pair in the form of a table:
| one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 | 15 | sixteen | 17 | 18 | nineteen | 20 | 21 | 22 | 23 |
| w | e | t | t | e | r | v | o | r | h | e | r | s | a | g | e | b | i | s | k | a | y | a |
| r | w | i | v | t | y | r | e | s | x | b | f | o | g | k | u | h | q | b | a | i | s | e |
Pay attention to the substitutions implemented by the enigma in 14, 15 and 20 positions. At step 14, the letter A is encrypted in G. The latter, in turn, is encrypted in K at step 15. And then the letter K is encrypted in A in step 20, thereby looping the AGKA chain. Such looped chains are called cycles. The presence of cycles allows you to divide the task of breaking Enigma into two simple components: 1) search for the starting position of the rotors and 2) search for connections of the patch panel with known rotor installations.
We know that several transformations occur during encryption in the Enigma. First, the signal passes through the patch panel. The result of the conversion on the switching panel enters the rotors. After that, the signal reaches the reflector and returns through the rotors to the switching panel, where the last substitution is performed. All these operations can be represented by a mathematical formula:
E i = S -1 R -1 TRS, where
S and S -1 , - conversion on the input and output switchboard, respectively;
R and R -1 - conversion in the rotors at the input and output;
T - conversion on the reflector.
Lowering the switch panel, we express the internal transformation of the Enigma through P i :
Pi = R -1 TR
Now encryption can be written as:
E i = S -1 P i S
Using the formula we rewrite the substitutions from the example in 14, 15 and 20 positions.
S -1 P 14 S (A) = G or that the same P 14 S (A) = S (G).
P 15 S (G) = S (K)
P 20 S (K) = S (A)
Replacing in the last expression S (K) we get:
P 20 P 15 P 14 S (A) = S (A) (1), where S (A) is the letter connected to A on the patch panel.
Now the attack is reduced to a trivial enumeration of all possible rotor settings. For each combination of rotors, it is necessary to verify the equality (1). If the equality is performed for the letter S, this means that the correct configuration of the rotors is found and that the letter A is connected to the switchboard with the letter S. The search for the remaining pairs is reduced to deciphering the cryptotext and comparing the result with known plaintext.
It should be noted that with a probability of 1/26 equality can be performed even if rotors are installed incorrectly, therefore, it is desirable to use several “cycles” to increase the reliability of the algorithm.
Another important point is that the attacker may only know part of the encrypted message. And in this case, first of all, he will need to find the location of the known text in the received cryptogram. The knowledge of the fact that Enigma never encrypts a letter into itself helps a great deal in this task. Those. To find the correct offset, you need to find such a position in the cryptotext in which none of the letters of the closed text is duplicated by the letter of the open message.
PS
A very slow, but quite working implementation of the Python attack can be viewed on GitHub .
Links
Source: https://habr.com/ru/post/269519/
All Articles