Job Search Guide for MDA Specialist (and a little about hierarchy analysis method, Xcore and Sirius)

This is the 4th article of the model-driven development cycle. In previous articles, we introduced OCL and metamodels , the Eclipse Modeling Framework, and Sirius . Today we will learn to describe metamodels in textual notation (and not in the form of diagrams as before) and get acquainted with the tabular presentation of models in Sirius. We do this on the example of the middle age crisis and the hierarchy analysis method. Perhaps this will be useful to you when developing AI in games, when making decisions or at work.

Introduction

Actually, I was planning an article on DSL development and model conversion. But my plans suddenly disturbed my thoughts about the meaning of life, about whether I was doing that at all.

The most obvious thing a model-driven development specialist can do is
')

• Choose a method that will provide answers of interest (section 1)
• Create a metamodel for this method (section 2)
• Create a model development tool in accordance with the metamodel (section 3)
• Create model (section 4)
• ...
• Profit

That is what we are going to do.

Note

If you are interested in the method of analyzing hierarchies, but you do not want to understand metamodels, etc., then an Excel calculator of priorities is available .

1 Hierarchy Analysis Method

I was interested in the following questions:

• What am I interested in doing?
• Do I have enough time for interesting things?
• What can be changed in life for the better?
• Wouldn't this change get worse?
• ...

When I studied at the university, we used the hierarchy analysis method to get answers to various questions. The essence of the method is as follows.

1. You define
   
   • target,
   • criteria for achieving the goal and
   • possible alternatives.
2. Evaluate the significance of the criteria.
3. Evaluate alternatives for each of the criteria.
4. Calculate the priorities of alternatives.
5. Make a decision.

This method is described in more detail in Thomas Saaty’s book Decision Making. The method of analyzing hierarchies "(it is easily googled). By the way, there are many examples from psychology to the global economy.

1.1 Construction hierarchy

So, in the simplest case, the hierarchy should contain a goal, criteria and alternatives.

To sum up all my questions, then, by and large, I’m wondering if I should change jobs. Therefore, the goal: to choose a job .

When choosing a job I'm interested in

• how much money I will earn
• how interesting it will be for me to do this
• will i have time to live
• career prospects
• will I be able to go to nature or will I see the sun and trees once a year,
• how close to me is the culture of colleagues, neighbors and other people.

The following alternatives are possible:

• change nothing
• move to Moscow
• move abroad,
• do freelancing or some kind of business.

In accordance with the method of analyzing hierarchies, the following hierarchy is constructed:

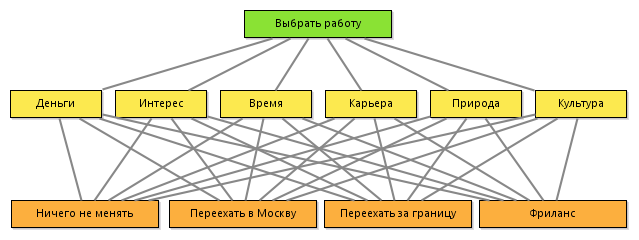
1.2 Evaluation of criteria

Different people may have approximately the same criteria when making decisions. However, their significance can vary greatly. Someone works more for the money, someone for the sake of interest, someone just likes to communicate with colleagues, etc.

In accordance with their priorities, one person will not hesitate to choose a more monetary job, and another - more interesting. There is no job that is absolutely suitable for all criteria.

Probably, when making decisions, most people explicitly or implicitly rank the criteria from the most significant to the most insignificant. The latter are discarded, and the first alternatives are compared. They put a label on every possible job: here, this work is more monetary, but not interesting, but this interesting and good team there, but dubious career prospects, etc.

If it is not possible at once to make a choice, then the person begins to overestimate the criteria: there may still be an interest not so important and you can stand for two hours in a traffic jam, but there is more salary, so I will pay the mortgage and I will do something interesting.

Such reasoning can go on for a long time, painfully and without guarantee that in the end the optimal decision will really be made.

The hierarchy analysis method proposes a formal algorithm for making such decisions: all criteria are compared in pairs with each other on a scale from 1 to 9.

For example, what is more important for me: interest or money? Interest is more important, but not to say that very much. If the maximum score is 9 to 1, then for myself I rate the priorities as 5 to 1.

Or, for example, what is more important: money or time for life, a hobby? Am I ready for extra money to work on weekends or stand for two hours in traffic jams? I for myself rate the significance of these criteria as 1 to 7.

As a result, a similar table is filled:



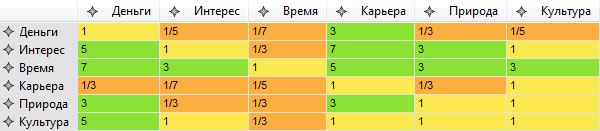
Obviously, diagonally there will always be units. It is also obvious that all estimates will be inversely symmetric with respect to the main diagonal. For example, if I estimate the importance of “interest-money” as 5 to 1, then the significance of “money-interest” will be 1 to 5. Sometimes such matrices are called back-symmetric.

In general, if we compare N criteria, then we need to make (N * (N-1)) / 2 comparisons. It would seem that everything is only complicated. If initially there were 6 criteria, now there is a whole matrix of some numbers. To return to the criteria again, calculate the eigenvector of the matrix. The elements of this vector will be the relative importance of each criterion.

The book by Thomas Saaty suggests several simplified methods for calculating the eigenvector in the mind or on paper. We will use a more accurate iterative algorithm :

N =   m =    NxN eigenvector =   N,   1/N   eigenvalue               x = m * eigenvector eigenvalue = sum(x) eigenvector = x / eigenvalue 

As a result, we obtain the following vector:

 [ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ] 

The most significant criterion is time (0.3846), the least significant is the career (0.0555).

With pairwise comparisons, some estimates may turn out to be inconsistent. For example, for me, interest is more important than money, and money is more important than a career. Obviously, interest must be significantly more important than a career. In this table it is. But if the assessment for the “interest-career” was less or not the opposite, then my estimates would not be consistent with each other.

Evaluate the measure of this inconsistency will help the eigenvalue of the matrix of comparisons. It is equal to 6.7048.

Obviously, the eigenvalue is proportional to the number of criteria. So that the assessment of consistency does not depend on the number of criteria, the so-called consistency index is calculated = (eigenvalue - N) / (N - 1).

Finally, in order for the assessment to be completely objective, it is necessary to divide this index by the average index of consistency for random matrices. If the value obtained (the ratio of consistency) is less than 0.1000, then the pairwise comparisons can be considered more or less consistent. In our example, it is 0.1137, which means that the calculated priorities can be more or less trusted.

1.3 Evaluating Alternatives

Now you need to compare all the alternatives for each of the criteria.



For example, when I move to Moscow, I will significantly win in salary. But work, most likely, will be less interesting, and also there will be less time for life. Or when moving abroad, I will have to give up my language, adjust to other people's cultural values.

For each criterion, an eigenvector and a consistency relation are calculated.

The resulting eigenvectors are written in columns:



The consistency relationship for each criterion is recorded in the following vector:

 [ 0,0337; 0,0211; 0,1012; 0,1399; 0,1270; 0,9507 ] 

Most values ​​are less or slightly higher than 0.1000. However, for the “culture” criterion, the consistency ratio was very large. This is due to the fact that I incorrectly set part of the ratings. I wanted to put 7 for “not to change anything - to move abroad”, because living in my hometown is much more comfortable. But mistakenly set 1/7.

1.4 Prioritization of Alternatives

So, we evaluated the criteria, put a label on each alternative: which option is more monetary, which is more interesting, etc. Now you need to evaluate alternatives for all criteria in the amount. To do this, simply multiply the matrix



by vector

 [ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ] 

As a result, we get the following vector:

 [ 0,3184; 0,1227; 0,2049; 0,3540 ] 

This is the relevance of alternatives to achieving the goal.

1.5 Decision Making

Now we draw all the calculated values ​​in the following image:



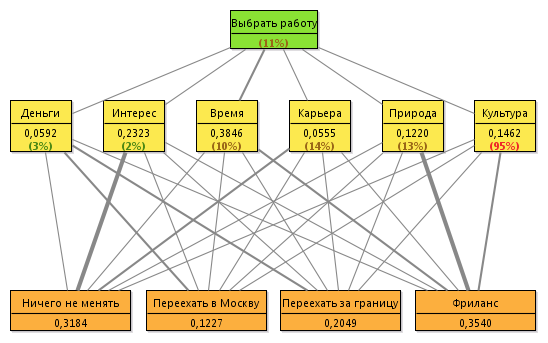
The brackets indicate the consistency of ratings.

The thickness of the lines is proportional to the priorities. The most interesting and promising career in terms of current work. Freelance would allow more to be in nature and more time to spend on life. More monetary work in Moscow and abroad.

It is evident that Moscow completely disappears. A little better abroad, but also not very much. Change nothing and freelancing about the same level.

2 Creating a metamodel

Now we will describe how all this is drawn and considered.

First, it is necessary to describe the metamodel: entity types that are used in the hierarchy analysis method. Moreover, unlike the previous article, we will not draw the metamodel in the form of a diagram, but describe it in Xcore textual notation.

As before, you will need Eclipse Modeling Tools . Install Xcore and Sirius.

You can either take the finished project or do it yourself. If on your own, create an Xcore project. In the model folder, create the file ahp.xcore with the following contents:

 @Ecore(nsURI="http://www.example.org/ahp") @GenModel( modelName="AHP", prefix="AHP", editDirectory="/xctest.edit/src-gen", editorDirectory="/xctest.editor/src-gen", testsDirectory="/xctest.tests/src-gen") package ahp class Hierarchy { contains Goal[1] goal contains Criterion[+] criteria contains Alternative[2..*] alternatives } interface Named { String[1] name } class Goal extends Named { } class Criterion extends Named { } class Alternative extends Named { } 

The meaning should be intuitive. We have described a hierarchy that contains one goal, at least one criterion, two or more alternatives. All three entities have a name.

After saving the file, the Java API for working with hierarchies in the src-gen folder is automatically generated. And also 3 additional projects will be created. We already did something similar in the EMF article . Only there were two models (ecore and genmodel), and we ran the code generation manually. Xcore does this automatically.

I think that there’s no point in describing the entire metamodel in the article, you can look at it yourself .

Let's stop only on the most interesting things. Xcore, unlike Ecore, allows describing not only the structure of the model, but also some logic in a Java-like language. We describe, for example, the type of data for storing ratings. Positive ratings will be stored as positive integers. And inverse estimates of the 1 / n type will be stored as -n. We could store the estimates as strings or as real numbers, but this is probably a bad idea.

At the same time, we need two functions to convert the estimates from or to the string representation. On Xcore, it will look like this:

 type Weight wraps int create { if (it.matches("\\d+")) { Integer.parseInt(it) } else if (it.matches("1\\s*/\\s*\\d+")) { val result = Integer.parseInt(it.replaceFirst("1\\s*/\\s*", "")) if (result <= 1) 1 else -result } else { throw new NumberFormatException("The weight must be either n or 1/n") } } convert { if (it >= 1) { it.toString } else if (it >= -1) { "1" } else { "1/" + (-it).toString } } 

Xcore also makes it possible to describe relatively complex logic.

Finally, for the Xcore model (as for the Ecore model) you can create a class diagram.



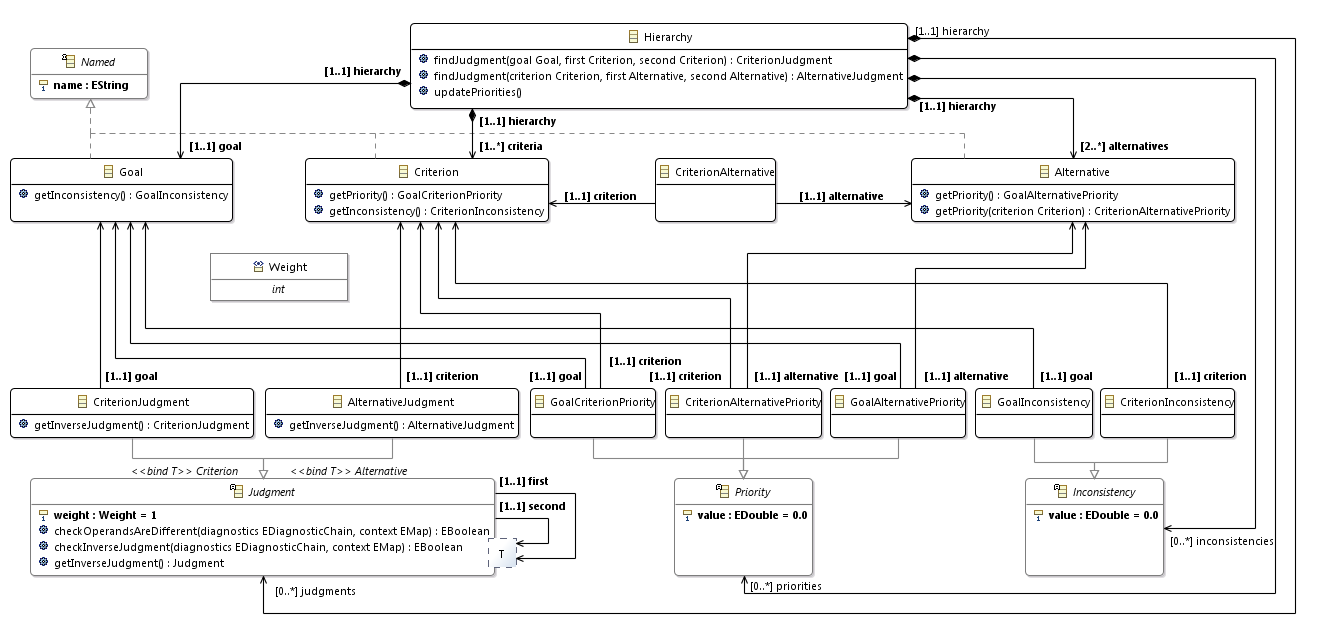
This is the meta model for the hierarchy analysis method. This is the most simplified version. In general, a hierarchy may contain more than three levels (for example, criteria may have subcriteria). Matrix connections between levels can be sparse. Ratings can put several experts, not one.

3 Development of a tool for working with models

Metamodel is ready, now you need an editor of hierarchies and matrices. Probably, it makes no sense to describe in detail how all this is done. If you're interested, you can read the previous article about Sirius and see the finished project .

This is the specification of the editor of charts and tables:



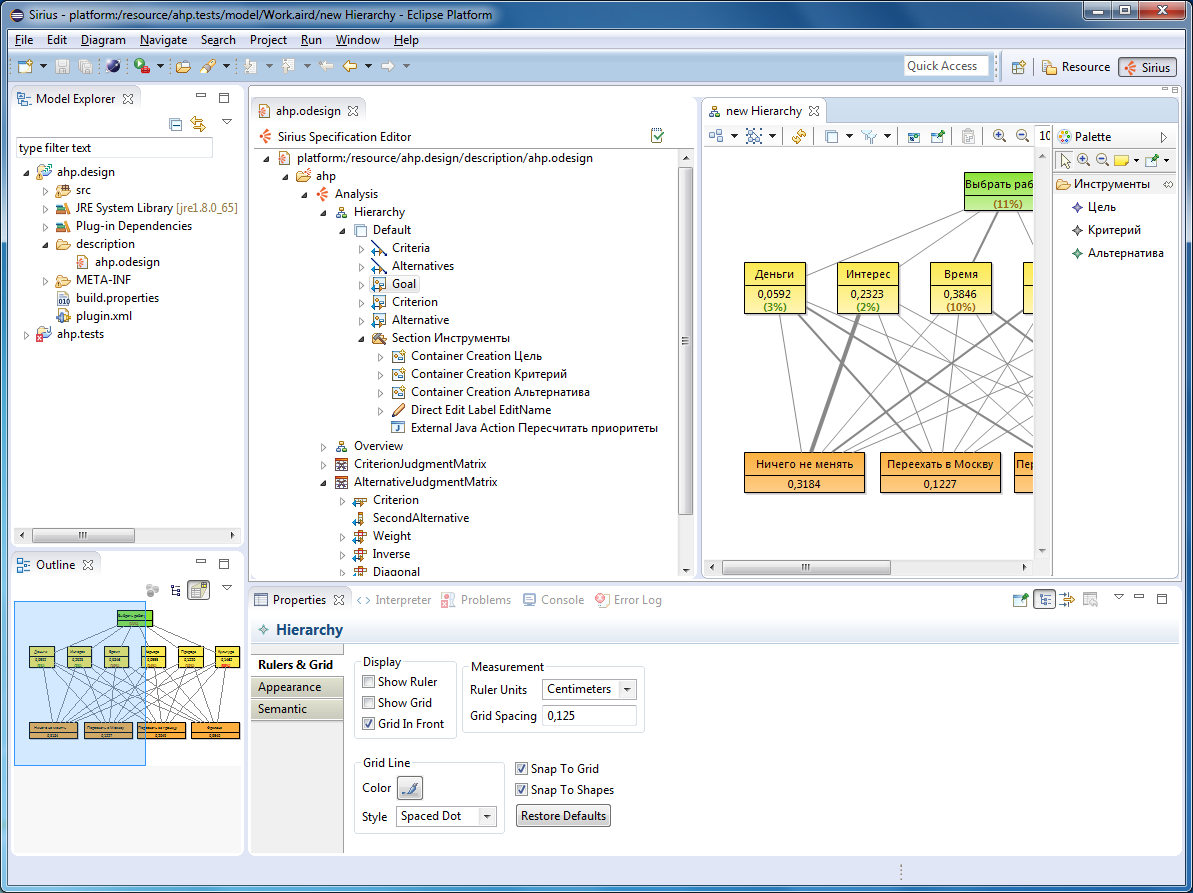
This is what the resulting editor looks like:



It was not possible to completely declare the hierarchy editor, I had to write extensions in Java. I think it is worthwhile to dwell on this in more detail. In Sirius there are at least two options for extensions: services (service) and actions (action).

Using services you can add some additional operations to the classes from the metamodel. For example, the following two operations format the priority accordingly and calculate the thickness of the connections between criteria and alternatives.

 public class Service { public String toString(Priority priority) { return String.format("%.4f", priority.getValue()); } public int getEdgeWidth(Alternative alternative, EdgeTarget targetView) { DSemanticDecorator targetNode = (DSemanticDecorator)targetView; Criterion criterion = (Criterion)targetNode.getTarget(); Priority priority = alternative.getPriority(criterion); return (int) (priority.getValue() * 7); } } 

Conveniently, you can use these operations directly in AQL expressions. However, you cannot change the model with their help.

To change the model you need to use Java actions. Actions, unlike services, can no longer be called in AQL expressions. They can be launched, for example, through the context menu or by pressing a button. Actions can be rolled back using the Undo command.

4 Creating a model

Well, actually, I have already created my model and showed it above. Try to take this project and build your hierarchy.

Profit

After reading this article, you should

• get a general idea of ​​the hierarchy analysis method,
• learn to describe metamodels in Xcore,
• learn how to create pivot tables using Sirius,
• Learn how to write extensions for Sirius in Java.