Geekly Articles each Day
📜 ⬆️ ⬇️

Blom scheme

image In June 2015, a block encryption standard was adopted in Russia - GOST R 34.12-2015. I was interested in combining this GOST (more precisely, the polynom used in it) and the Blom scheme.

Armed with the source code and the GOST itself, I got down to business. But first, a little theory.

So, the Blom Scheme is a pre-key distribution scheme for a network. The principle of its operation is as follows:

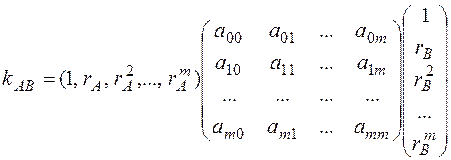
image
')
There is a symmetric square matrix T :

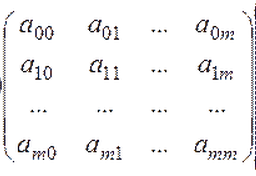
image

The matrix, as a rule, contains as many rows (and columns) as there are subscribers in the network. So, with 20 subscribers, the matrix has a size of at least 20 * 20.

Public keys of subscribers A and B :

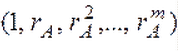
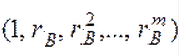
image

image

Public keys, as a rule, are formed according to the principle of the Vandermort matrix, where the first element of a row is a number to the zero degree, the second number is to the first number, and the nth number is to the nth degree. In our program, the first element of each line will be a number in the first degree, and not in zero:

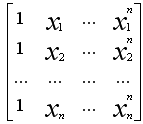image .

This is how all public keys for all obonents are formed.

If we take subscriber A's public key and multiply it by matrix T, we get subscriber A's secret key :

image

The same is done for all subscribers of the network. This is done by a trusted party, who then distributes a public and private key to each participant. Participants, exchanging among themselves only public keys via unprotected communication channels, can generate a secret session key to communicate with each other.

The reliability of the scheme depends on the size of the secret matrix used in the scheme. To recover a secret matrix, you must have a number of keys equal to the number of rows of the matrix. After that, the secret key of subscriber A is multiplied by the public key of subscriber B - this is how the session key is obtained.

For clarity, a small example on small numbers, taken here :

The trusted center selects the size of the final field and the secret matrix:

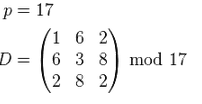
image

Subscribers choose their identifiers (usually issued by a trusted center):



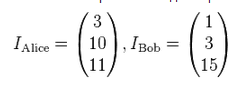
The trusted authority calculates private keys:



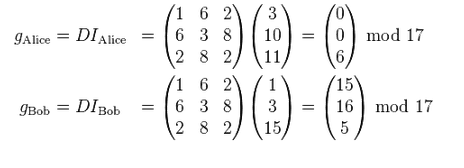
After that, each of the parties calculates the secret key, multiplying its private key by the identifier of the second party:



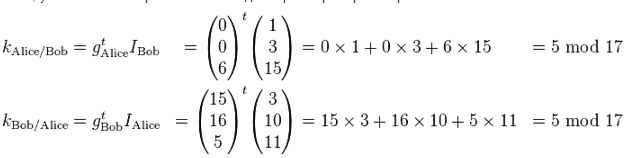
As seen in the example, the same key is obtained.

To rub we implement it in C ++


To begin with we will create and we will fill our matrix. For clarity, we will make it 8 * 8:

randomize(); for (int i = 0; i < 8; i++) { for (int j = 0; j < 8; j++) { if (j >= i) { mass[i][j] = random(255); } } } for (int i = 0; i < 8; i++) { for (int j = 0; j < 8; j++) { mass[j][i] = mass[i][j]; } }

Also we will connect to our project table.h, in which, in fact, all possible multiplications of the polynomial, which is used in GOST, on itself, just shifted, are recorded.

 #include "table.h"

We initialize variables which will be useful to us:

  int zakr3[8] = {NULL}; //  int zakr2[8] = {NULL}; //  int abon3[8] = {NULL}; //  int abon2[8] = {NULL}; //  int secret3[8] = {NULL};//  int secret2[8] = {NULL}; //

In the Edit, we enter the numbers of subscribers, which are then read:

  abon2[0] = StrToInt(Edit1->Text); abon3[0] = StrToInt(Edit2->Text);

Further, using the principle of the Vandermorta matrix, we “finish off” the lines of public keys to complete:

 for (int j = 1; j < 8; j++) { sum3 = multTable[abon3[j - 1] + 256 * StrToInt(Edit1->Text)]; sum2 = multTable[abon2[j - 1] + 256 *StrToInt(Edit2->Text)]; abon2[j] = sum2; //  abon3[j] = sum3; //  }

multTable is the same table.h that we connected earlier. It's time to generate private keys:

  for (int j = 0; j < 8; j++) { int x1= 0,x2 = 0; //  for (int y = 0; y < 8; y++) { sum3 = multTable[mass[j][y] + 256 * abon3[y]]; sum2 = multTable[mass[j][y] + 256 * abon2[y]]; x1 = x1^ sum3; x2 =x2 ^ sum2; } //  : zakr3[j] = x1; zakr2[j] = x2; }

Here the rule of multiplying a row by a matrix is ​​applied, with the exception that instead of the usual addition we use addition modulo 2. As a result, we get a row consisting of 8 elements.

Next, we have to calculate the shared secret key.

  sum3 = NULL; sum2 = NULL; for (int y = 0; y < 8; y++) { secret3[y] = multTable[256 * zakr3[y] + abon2[y]]; //  secret2[y] = multTable[256 * zakr2[y] + abon3[y]]; //  sum3 = sum3 ^ secret3[y]; //    sum2 = sum2 ^ secret2[y];//    }

This is where the row is multiplied by the column. The result is a number. If done correctly, sum2 and sum3 should be the same. That's basically it. In this example, I used int-native numbers, but no one forbids the use of numbers of higher dimension.

Sources:

Source: https://habr.com/ru/post/269229/

More articles:


All Articles