Do-it-yourself audio codec
current edition of the article on the Makeloft website
I think that for many people , lossy audio compression resembles a magical black box, where in a surprisingly complex way using mathematical alchemy, data is compressed due to loss of redundant information, poorly distinguished or inaudible human ear, and, as a result, some reduction in recording quality. However, immediately assess the materiality of such losses and understand their essence is not very easy. But today we will try to find out what is the matter there and thanks to what a similar data compression process is possible dozens of times ...
It is time to remove the curtain, open the door and take a first look at the mysterious algorithm disturbing the minds and hearts, welcome to the exposing session !
')
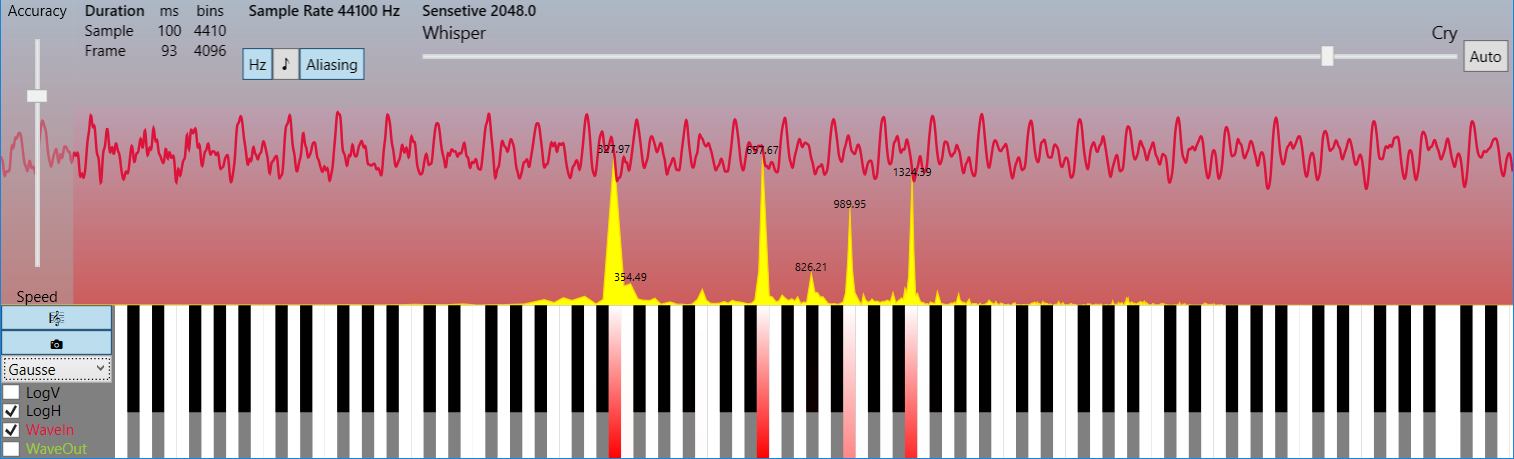
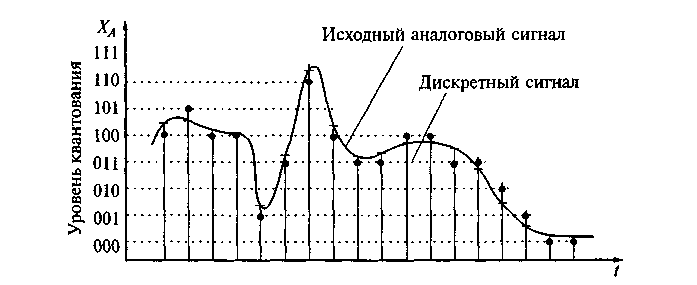
An uncompressed audio stream is an array of integers ( C # short ), for example, coming from the microphone's buffer. It is a discrete set of amplitude values of an analog signal taken at regular intervals (that is, with a certain sampling rate and level quantization).
* for simplicity, hereinafter we will consider the classic mono signal
If you immediately write this array to a file, then even a short time interval will turn out to be quite voluminous. It is clear that, apparently, in such a streaming signal contains a lot of redundant data, so the question arises how to select the right and remove the redundant? The answer is simple and harsh - use Fourier transform .
Yes, the very thing that we regularly talk about at technical universities and that, we successfully manage to forget. However, it does not matter - we study the introductory presentation and read the article , where the issue is considered in more than detail. We only need the algorithm itself, the size of which is only 32 lines of C # code.
The conversion is applied to small portions of the signal — frames with a number of samples of a power of two, which is usually 1024 , 2048 , 4096 . With a standard sampling rate of 44100 Hz , which, according to the Kotelnikov-Nyquist-Shannon theorem, allows to restore the original signal without distortion with a maximum frequency in the spectrum up to 22050 Hz , which corresponds to the maximum frequency threshold of hearing of the human ear, these passages are equivalent in duration to approximately 23 , 46 and 93 ms, respectively. Then we get an array of complex numbers (of the same length as the frame), which contains information about the phase and frequency spectra of a given fragment of the signal. The resulting array consists of two mirror parts-copies, so only half of its elements have real information content.
At this stage, just as we can remove information about quiet frequencies, retaining only loud ones , for example, in the form of a dictionary, and during playback, restore the lost elements, replacing them with zero ones, then perform the inverse Fourier transform and get a suitable playback signal. It is on this principle that the work of a huge number of audio codecs is based, since the described operation makes it possible to compress dozens and even hundreds of times (!). Of course, the method of recording information in the file also makes its own adjustments to the resulting size and the additional use of lossless archiving algorithms is far from superfluous, but the most significant contribution is provided by the silencing of inaudible frequencies .
At first, it’s hard to believe that such significant compression ratios can be achieved in such a trivial way, but if you look at the spectral image on a linear frequency scale rather than a logarithmic one, you will immediately see that only a narrow set of harmonics carrying useful information is usually present in the real spectrum. and all the rest is a slight noise that lies beyond hearing. And, paradoxically, at low degrees of compression, the signal does not spoil for perception, but, on the contrary, is only cleared of noise, that is, idealized!

* The pictures show a frame in 4096 counts (93 ms) and a frequency spectrum up to 22050 Hz (see LimitFrequency in source codes). This example demonstrates how low the harmonics in real signals are.
In order not to be unsubstantiated, I suggest testing a demo application ( Rainbow Framework ) , where the compression algorithm is trivially simple, but it is fully operational. At the same time, you can assess the distortions that occur depending on the degree of compression, as well as explore ways of visualizing sound and much more ...
Yes, of course, there are puzzling algorithms that take into account the psycho-acoustic model of perception, the likelihood of the appearance of certain frequencies in the spectrum, etc., etc., but they all only help to partially improve performance while maintaining decent quality, while the lion's share of compression is achieved by such uncomplicated in a way that literally only a few lines in C #.
So, the general scheme of compression is as follows:
1. Splitting the signal into amplitude-time frames *
2. Forward Fourier transform - obtaining amplitude-frequency frames
3. Complete silencing of silent frequencies and additional optional processing.
4. Write data to file
* often frames partially overlap each other, which helps to avoid clicks when a signal of a certain harmonic begins or ends in one frame, but is still weak and will be muffled in it, although in another frame its sound is gaining full strength and not muffled. Because of what, depending on the phase of the sinusoid, a sharp jump in amplitude at the boundaries of non-overlapped frames is possible, perceived as a click.
The reverse process includes the following steps:
1. Reading a file
2. Recovery of amplitude-frequency frames
3. The inverse Fourier transform - obtaining amplitude-time frames
4. Formation of a signal from amplitude-time frames
That's all. Perhaps you were expecting something much more complex?
References:
1. Introductory presentation
2. Fourier Transform Article
3. Demo application with source codes (Rainbow Framework)
( backup link )
I think that for many people , lossy audio compression resembles a magical black box, where in a surprisingly complex way using mathematical alchemy, data is compressed due to loss of redundant information, poorly distinguished or inaudible human ear, and, as a result, some reduction in recording quality. However, immediately assess the materiality of such losses and understand their essence is not very easy. But today we will try to find out what is the matter there and thanks to what a similar data compression process is possible dozens of times ...
It is time to remove the curtain, open the door and take a first look at the mysterious algorithm disturbing the minds and hearts, welcome to the exposing session !
')

An uncompressed audio stream is an array of integers ( C # short ), for example, coming from the microphone's buffer. It is a discrete set of amplitude values of an analog signal taken at regular intervals (that is, with a certain sampling rate and level quantization).

* for simplicity, hereinafter we will consider the classic mono signal
If you immediately write this array to a file, then even a short time interval will turn out to be quite voluminous. It is clear that, apparently, in such a streaming signal contains a lot of redundant data, so the question arises how to select the right and remove the redundant? The answer is simple and harsh - use Fourier transform .
Yes, the very thing that we regularly talk about at technical universities and that, we successfully manage to forget. However, it does not matter - we study the introductory presentation and read the article , where the issue is considered in more than detail. We only need the algorithm itself, the size of which is only 32 lines of C # code.
public static Complex[] DecimationInTime(this Complex[] frame, bool direct) { if (frame.Length == 1) return frame; var frameHalfSize = frame.Length >> 1; // frame.Length/2 var frameFullSize = frame.Length; var frameOdd = new Complex[frameHalfSize]; var frameEven = new Complex[frameHalfSize]; for (var i = 0; i < frameHalfSize; i++) { var j = i << 1; // i = 2*j; frameOdd[i] = frame[j + 1]; frameEven[i] = frame[j]; } var spectrumOdd = DecimationInTime(frameOdd, direct); var spectrumEven = DecimationInTime(frameEven, direct); var arg = direct ? -DoublePi / frameFullSize : DoublePi / frameFullSize; var omegaPowBase = new Complex(Math.Cos(arg), Math.Sin(arg)); var omega = Complex.One; var spectrum = new Complex[frameFullSize]; for (var j = 0; j < frameHalfSize; j++) { spectrum[j] = spectrumEven[j] + omega * spectrumOdd[j]; spectrum[j + frameHalfSize] = spectrumEven[j] - omega * spectrumOdd[j]; omega *= omegaPowBase; } return spectrum; } The conversion is applied to small portions of the signal — frames with a number of samples of a power of two, which is usually 1024 , 2048 , 4096 . With a standard sampling rate of 44100 Hz , which, according to the Kotelnikov-Nyquist-Shannon theorem, allows to restore the original signal without distortion with a maximum frequency in the spectrum up to 22050 Hz , which corresponds to the maximum frequency threshold of hearing of the human ear, these passages are equivalent in duration to approximately 23 , 46 and 93 ms, respectively. Then we get an array of complex numbers (of the same length as the frame), which contains information about the phase and frequency spectra of a given fragment of the signal. The resulting array consists of two mirror parts-copies, so only half of its elements have real information content.
At this stage, just as we can remove information about quiet frequencies, retaining only loud ones , for example, in the form of a dictionary, and during playback, restore the lost elements, replacing them with zero ones, then perform the inverse Fourier transform and get a suitable playback signal. It is on this principle that the work of a huge number of audio codecs is based, since the described operation makes it possible to compress dozens and even hundreds of times (!). Of course, the method of recording information in the file also makes its own adjustments to the resulting size and the additional use of lossless archiving algorithms is far from superfluous, but the most significant contribution is provided by the silencing of inaudible frequencies .
At first, it’s hard to believe that such significant compression ratios can be achieved in such a trivial way, but if you look at the spectral image on a linear frequency scale rather than a logarithmic one, you will immediately see that only a narrow set of harmonics carrying useful information is usually present in the real spectrum. and all the rest is a slight noise that lies beyond hearing. And, paradoxically, at low degrees of compression, the signal does not spoil for perception, but, on the contrary, is only cleared of noise, that is, idealized!

* The pictures show a frame in 4096 counts (93 ms) and a frequency spectrum up to 22050 Hz (see LimitFrequency in source codes). This example demonstrates how low the harmonics in real signals are.
In order not to be unsubstantiated, I suggest testing a demo application ( Rainbow Framework ) , where the compression algorithm is trivially simple, but it is fully operational. At the same time, you can assess the distortions that occur depending on the degree of compression, as well as explore ways of visualizing sound and much more ...
var fftComplexFrequencyFrame = inputComplexTimeFrame.DecimationInTime(true); var y = 0; var original = fftComplexFrequencyFrame.ToDictionary(c => y++, c => c); var compressed = original.OrderByDescending(p => p.Value.Magnitude).Take(CompressedFrameSize).ToList(); Yes, of course, there are puzzling algorithms that take into account the psycho-acoustic model of perception, the likelihood of the appearance of certain frequencies in the spectrum, etc., etc., but they all only help to partially improve performance while maintaining decent quality, while the lion's share of compression is achieved by such uncomplicated in a way that literally only a few lines in C #.
So, the general scheme of compression is as follows:
1. Splitting the signal into amplitude-time frames *
2. Forward Fourier transform - obtaining amplitude-frequency frames
3. Complete silencing of silent frequencies and additional optional processing.
4. Write data to file
* often frames partially overlap each other, which helps to avoid clicks when a signal of a certain harmonic begins or ends in one frame, but is still weak and will be muffled in it, although in another frame its sound is gaining full strength and not muffled. Because of what, depending on the phase of the sinusoid, a sharp jump in amplitude at the boundaries of non-overlapped frames is possible, perceived as a click.
The reverse process includes the following steps:
1. Reading a file
2. Recovery of amplitude-frequency frames
3. The inverse Fourier transform - obtaining amplitude-time frames
4. Formation of a signal from amplitude-time frames
That's all. Perhaps you were expecting something much more complex?
References:
1. Introductory presentation
2. Fourier Transform Article
3. Demo application with source codes (Rainbow Framework)
( backup link )
Source: https://habr.com/ru/post/268905/
All Articles