Three-Way Bitwise Quick Sort
Hello! Today we will talk about not the most famous sorting algorithm - three-way bitwise quick sorting. This algorithm is a hybrid of the well-known quick sort and bitwise sort.
Details - under the cut.
But first, remember the old one.
She knows most. If we briefly take a supporting element, we make exchanges so that on one side of it there are smaller elements in the array, on the other - larger or equal. Next, we run recursively the same procedure on the resulting parts. At the same time, the support element itself has already appeared on the place where it will be in the sorted array.
')
At the same time, they often talk about optimizations for quick sorting. The best-known optimization is to select the reference element at random. Thus, the probability of “hitting” is significantly reduced in the case when quick sorting shows the worst performance (O (n ^ 2), as we all remember).
The second most popular idea is to divide an array not into two, but into three parts. Elements less than the reference, equal to it and elements greater than the reference. This optimization significantly speeds up the execution time in cases where there are many identical elements in the source array — after all, the same support elements as well as the reference elements have already “fallen” into their place in the sorted array, and no additional procedures are needed to sort them. The number of operations performed and the depth of recursive calls decrease. In general, a good way to save a little.
Difficulty - O (nlogn) on average, O (n ^ 2) at worst, additional memory - O (logn)
If anything, here is a good and briefly written.
Slightly less popular algorithm, but quite well known. The logic of his work is simple. Suppose we have an array of numbers.
First, sort them by the first (senior) category. Sorting in this case is performed using count sorting. The complexity is o (n). We received 10 "baskets" - in which the senior level 0, 1, 2, etc. Then we run the same procedure in each of the baskets, but we only consider not the high order, but the next one, and so on.
There are as many steps as digits in numbers. Accordingly, the complexity of the algorithm is O (n * k), k is the number of digits.
There are two types of such sorting - MSD (most significant digit - first high order) and LSD (least significant digit first low end). LSD is somewhat more convenient for sorting numbers, since it is not necessary to “assign” to the left insignificant 0 to align the number of digits.
MSD is more convenient for sorting rows.
The algorithm in this implementation requires additional memory - O (n).
You can read more, for example, here .
Suppose we are sorting the rows.
Using qsort, which actively compares elements, looks too expensive - string comparison is a long operation. Yes, we can write our comparator, which will be somewhat more efficient. But still.
Using radix, which requires additional memory, is also not very motivating - the lines can be large. Yes, and a large length of lines the number of discharges, depressing effect on efficiency.
And what if in some way to combine these algorithms?
The logic of the resulting algorithm is as follows:
1. Take the supporting element.
2. We divide the array into three parts, comparing the elements with the reference one according to the senior category - into smaller, equal and larger ones.
3. In each of the three parts, we repeat the procedure, starting from step No. 1, until we reach empty parts or parts with 1 element.
Only in the middle part (i.e., where the most significant bit is equal to the highest level of the support element) proceed to the next category. In the remaining parts of the operation begins without changing the "working" discharge.
The sorting complexity is O (nlogn). Additional memory - O (1).
The disadvantage of this algorithm is that, unlike bitwise sorting, it splits the array into only three parts, which, for example, limits the capabilities of a multi-threaded implementation. The advantage over quick sorting is that we don’t need to compare the elements as a whole. The advantage over bitwise sorting is that we don’t need additional memory.
Separately, it is worth noting that this sorting is convenient to use when the element of the original array is another array. Then, if the source array is input, then, for example, the high-order bit is input [i] [0], the next one is input [i] [1], and so on. This sort is called multi-dimensional quick sort, or multikey quicksort.
More and more detailed - R. Sedgwick, Fundamental Algorithms in C ++, Part 3, Chapter 10, 10.4 “Three-Path Bitwise Sort”
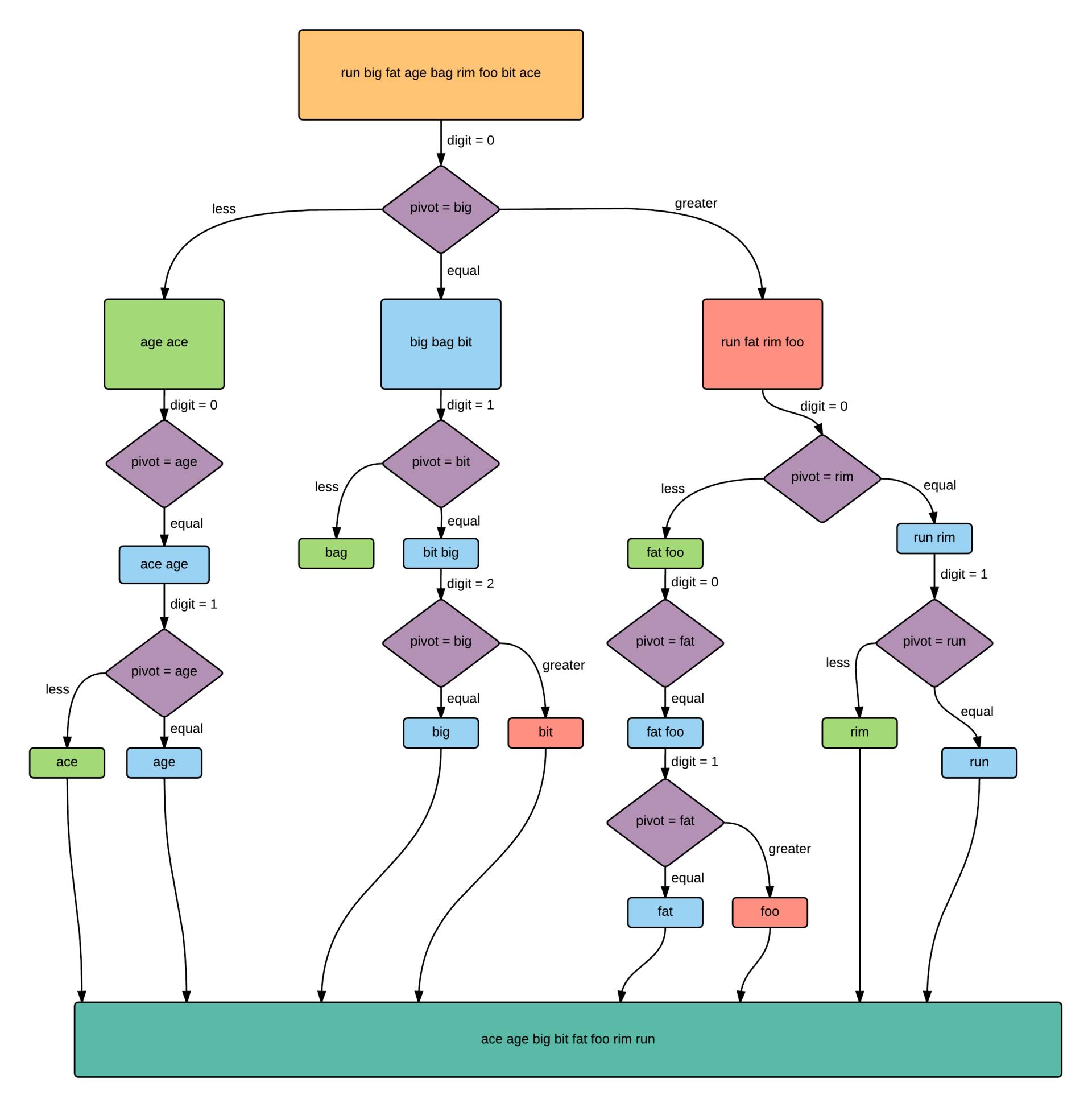
The scheme of the algorithm:
Note that the easiest way to implement the division of the array into three parts of the reference is to use the algorithm of Bentley and McIlroy. It lies in the fact that the following addition is made to the standard qsort separation procedure (immediately after the exchange of elements).
If the processed element is in the left part of the array (that is, it is not more than the reference one) and it is equal to the reference one, then it is placed in the left part of the array by exchanging with the corresponding element (which has already been completely processed and therefore less than the reference one). Similarly, if the processed element is in the right side of the array and is equal to the reference one, then it is placed in the right side of the array.
After the separation procedure is completed, when the number of elements less than the reference is already known, transfer of equal elements to the middle of the array (immediately after the elements smaller than the reference) is performed.
You can read about it in detail in R. Sedgwick - Fundamental Algorithms in C ++, p.3, ch.7, p.7.6 "Duplicate Keys".
Details - under the cut.
But first, remember the old one.
Quick sort (QSort)
She knows most. If we briefly take a supporting element, we make exchanges so that on one side of it there are smaller elements in the array, on the other - larger or equal. Next, we run recursively the same procedure on the resulting parts. At the same time, the support element itself has already appeared on the place where it will be in the sorted array.
')
At the same time, they often talk about optimizations for quick sorting. The best-known optimization is to select the reference element at random. Thus, the probability of “hitting” is significantly reduced in the case when quick sorting shows the worst performance (O (n ^ 2), as we all remember).
The second most popular idea is to divide an array not into two, but into three parts. Elements less than the reference, equal to it and elements greater than the reference. This optimization significantly speeds up the execution time in cases where there are many identical elements in the source array — after all, the same support elements as well as the reference elements have already “fallen” into their place in the sorted array, and no additional procedures are needed to sort them. The number of operations performed and the depth of recursive calls decrease. In general, a good way to save a little.
Difficulty - O (nlogn) on average, O (n ^ 2) at worst, additional memory - O (logn)
If anything, here is a good and briefly written.
Bitwise sorting (Radix Sort)
Slightly less popular algorithm, but quite well known. The logic of his work is simple. Suppose we have an array of numbers.
First, sort them by the first (senior) category. Sorting in this case is performed using count sorting. The complexity is o (n). We received 10 "baskets" - in which the senior level 0, 1, 2, etc. Then we run the same procedure in each of the baskets, but we only consider not the high order, but the next one, and so on.
There are as many steps as digits in numbers. Accordingly, the complexity of the algorithm is O (n * k), k is the number of digits.
There are two types of such sorting - MSD (most significant digit - first high order) and LSD (least significant digit first low end). LSD is somewhat more convenient for sorting numbers, since it is not necessary to “assign” to the left insignificant 0 to align the number of digits.
MSD is more convenient for sorting rows.
The algorithm in this implementation requires additional memory - O (n).
You can read more, for example, here .
Three-Way Bitwise Sorting
Suppose we are sorting the rows.
Using qsort, which actively compares elements, looks too expensive - string comparison is a long operation. Yes, we can write our comparator, which will be somewhat more efficient. But still.
Using radix, which requires additional memory, is also not very motivating - the lines can be large. Yes, and a large length of lines the number of discharges, depressing effect on efficiency.
And what if in some way to combine these algorithms?
The logic of the resulting algorithm is as follows:
1. Take the supporting element.
2. We divide the array into three parts, comparing the elements with the reference one according to the senior category - into smaller, equal and larger ones.
3. In each of the three parts, we repeat the procedure, starting from step No. 1, until we reach empty parts or parts with 1 element.
Only in the middle part (i.e., where the most significant bit is equal to the highest level of the support element) proceed to the next category. In the remaining parts of the operation begins without changing the "working" discharge.
The sorting complexity is O (nlogn). Additional memory - O (1).
The disadvantage of this algorithm is that, unlike bitwise sorting, it splits the array into only three parts, which, for example, limits the capabilities of a multi-threaded implementation. The advantage over quick sorting is that we don’t need to compare the elements as a whole. The advantage over bitwise sorting is that we don’t need additional memory.
Separately, it is worth noting that this sorting is convenient to use when the element of the original array is another array. Then, if the source array is input, then, for example, the high-order bit is input [i] [0], the next one is input [i] [1], and so on. This sort is called multi-dimensional quick sort, or multikey quicksort.
More and more detailed - R. Sedgwick, Fundamental Algorithms in C ++, Part 3, Chapter 10, 10.4 “Three-Path Bitwise Sort”
The scheme of the algorithm:

Once again about the three-way separation
Note that the easiest way to implement the division of the array into three parts of the reference is to use the algorithm of Bentley and McIlroy. It lies in the fact that the following addition is made to the standard qsort separation procedure (immediately after the exchange of elements).
If the processed element is in the left part of the array (that is, it is not more than the reference one) and it is equal to the reference one, then it is placed in the left part of the array by exchanging with the corresponding element (which has already been completely processed and therefore less than the reference one). Similarly, if the processed element is in the right side of the array and is equal to the reference one, then it is placed in the right side of the array.
After the separation procedure is completed, when the number of elements less than the reference is already known, transfer of equal elements to the middle of the array (immediately after the elements smaller than the reference) is performed.
You can read about it in detail in R. Sedgwick - Fundamental Algorithms in C ++, p.3, ch.7, p.7.6 "Duplicate Keys".
Source: https://habr.com/ru/post/268261/
All Articles