Candy Challenge (improving the result)
On September 28, viktorpanasiuk published a task , the solution of which is intended to reduce the production costs of a well-known confectionary factory, making its product more competitive in the market and more accessible to the buyer.
It was necessary to find the maximum permissible deviation of the mass of candy during its production, so that the net of a box consisting of 12 pieces of them did not go beyond 310 ± 7 grams in 90% of cases. The distribution law is considered normal.
The answer was that if the standard deviation mass of candy in the production does not exceed
mass of candy in the production does not exceed 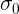 = 1.2248, this value is not limited from above.
= 1.2248, this value is not limited from above.
')
Under the cut, you can expect an improvement in the result obtained for the absolute value of some, I think - reasonable, assumptions. The following is not set out strictly enough, but still requires knowledge of mathematical analysis and probability theory in the scope of a technical college.
Let the mass of the box be a normally distributed random variable. Let the masses of candies are identical independent in the aggregate absolutely continuous random variables, with the expectation of 310/12. Let the density of the distribution is symmetric with respect to the expectation and do not increase to the right of the expectation (respectively, does not decrease to the left). Let the standard deviation of the masses of candies and
and 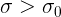 .
.
Estimate the maximum permissible deviation of the candy mass from below.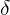 .
.
Since the mathematical expectation of the masses of candies does not affect the decision, in the future I will operate with centered random variables.
Obviously when The required condition will be fulfilled with probability 1. Below, I will show how this estimate can be improved to
The required condition will be fulfilled with probability 1. Below, I will show how this estimate can be improved to  .
.
Let f be the distribution density of the candy mass. Then, due to the definition of conditional probability, the new distribution density will be: .
.
At the same time, a new random variable should have a standard deviation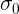 .
.
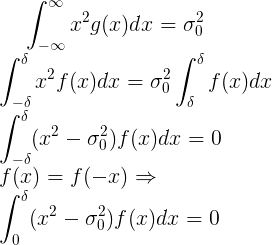
Solving the resulting equation for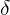 we obtain the desired estimate for a known distribution density f.
we obtain the desired estimate for a known distribution density f.
For further discussion, we need the following lemma:
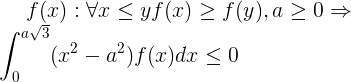
Evidence:
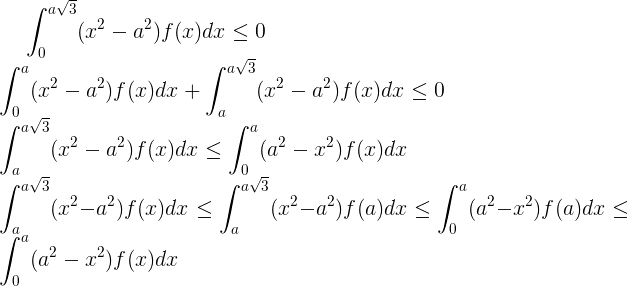
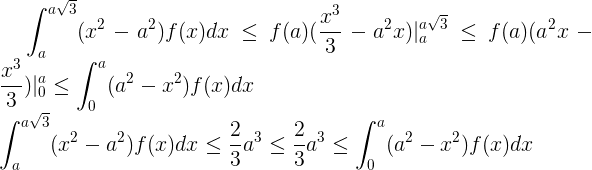
chd
Note that if for x <a there is a set of positive measure where f (x )> f (a) or for a <x <a 3 ^ (1/2) there is a set of positive measure where f (x) <f (a) then the inequality in the formulation of the lemma will be strict.
It is easy to show that if f is the distribution density of a uniform random variable with a mean of 0 and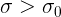 then
then  .
.
Then, applying the lemma, we find that if the distribution of the mass of candies is unknown, but belongs to the described class, then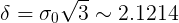 .
.
What else can be done: assess the applicability of the CLT (using the chi square test or the Berry – Esseen inequality), find how much the obtained estimate is worse than optimal with known distributions.
Thanks to those who read to the end. Love math.
It was necessary to find the maximum permissible deviation of the mass of candy during its production, so that the net of a box consisting of 12 pieces of them did not go beyond 310 ± 7 grams in 90% of cases. The distribution law is considered normal.
The answer was that if the standard deviation
 mass of candy in the production does not exceed
mass of candy in the production does not exceed 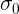 = 1.2248, this value is not limited from above.
= 1.2248, this value is not limited from above.')
Under the cut, you can expect an improvement in the result obtained for the absolute value of some, I think - reasonable, assumptions. The following is not set out strictly enough, but still requires knowledge of mathematical analysis and probability theory in the scope of a technical college.
Let the mass of the box be a normally distributed random variable. Let the masses of candies are identical independent in the aggregate absolutely continuous random variables, with the expectation of 310/12. Let the density of the distribution is symmetric with respect to the expectation and do not increase to the right of the expectation (respectively, does not decrease to the left). Let the standard deviation of the masses of candies
 and
and 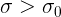 .
.Estimate the maximum permissible deviation of the candy mass from below.
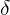 .
.Since the mathematical expectation of the masses of candies does not affect the decision, in the future I will operate with centered random variables.
Obviously when
 The required condition will be fulfilled with probability 1. Below, I will show how this estimate can be improved to
The required condition will be fulfilled with probability 1. Below, I will show how this estimate can be improved to  .
.Let f be the distribution density of the candy mass. Then, due to the definition of conditional probability, the new distribution density will be:
 .
.At the same time, a new random variable should have a standard deviation
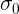 .
.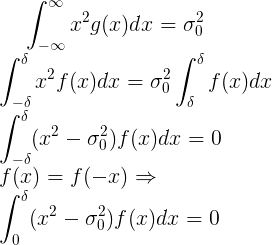
Solving the resulting equation for
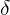 we obtain the desired estimate for a known distribution density f.
we obtain the desired estimate for a known distribution density f.For further discussion, we need the following lemma:
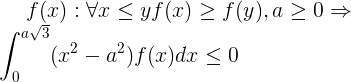
Evidence:
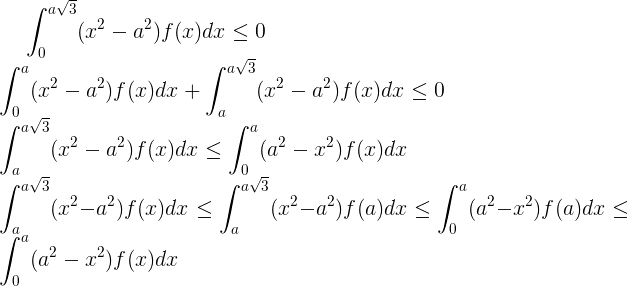
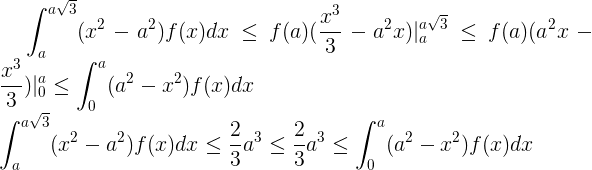
chd
Note that if for x <a there is a set of positive measure where f (x )> f (a) or for a <x <a 3 ^ (1/2) there is a set of positive measure where f (x) <f (a) then the inequality in the formulation of the lemma will be strict.
It is easy to show that if f is the distribution density of a uniform random variable with a mean of 0 and
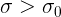 then
then  .
.Then, applying the lemma, we find that if the distribution of the mass of candies is unknown, but belongs to the described class, then
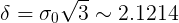 .
.What else can be done: assess the applicability of the CLT (using the chi square test or the Berry – Esseen inequality), find how much the obtained estimate is worse than optimal with known distributions.
Thanks to those who read to the end. Love math.
Source: https://habr.com/ru/post/268235/
All Articles