Financial Computing Challenge
In finance, there are tasks for evaluating investment projects, in which there are a number of indicators on the values of which are given a general assessment. These are indicators such as the payback period of a project, reduced income, net present income, etc. As a rule, to determine each of the indicators, there are formulas in which, simply, you need to substitute the source data, calculate and get the result. But there is one of the indicators that cannot be solved by simple substitution of data into a formula. This indicator is called the " internal rate of return ". Currently, there are a large number of different software for financiers, which allows you to conduct all the calculations automatically, without thinking about how everything happens inside.
So, suppose we are given a table in which the data of some investment project are given:
Where:
C - initial investment (the value is always negative);
Vj - financial income from the project in the j-th period;
j is the sequence number of the period (calendar year).
Also, we are given the annual percentage discount rate - i .
We need to determine the internal rate of return of this project - IRR .
The internal rate of return is calculated as follows: you need to choose the value of the interest rate IRR , so that the equation is solved:
In our case, the initial investment (investment) in the project was made only once, according to a given table - in the zero year, respectively, the above equation will take the following form:
To determine the internal rate of return, you still need a formula for determining the total net present value ( NPV ) for five periods of financial income:
Where PVj is the reduced income for the j-th period:
If replaced by the expression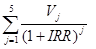
expression 
in the formula for determining the reduced income PV , which is then substituted into the formula for determining the total net present income of NPV , then we obtain the following function:
If we replace the desired value of IRR at which
the value of the interest rate r which varies in the interval from 0 to 100%, then we get the function:
the graph of which is presented in the figure below:
The graph shows that the task of finding the internal rate of return IRR (NPV (IRR) = 0) is reduced to finding the intersection point of the graph with the x -axis, which can be found using any of the numerical methods.
Take, for example, Newton's numerical method . Having the data, from the given table, let's make a power function of one variable x for the investment project:
The sequence of approximation to the value of the discount multiplier is constructed from the initial value x0 = 1 by the following formula:
Where:
k is the iteration step number;
- derivative of power function:
Each newly calculated xk value is substituted into the formula
(this formula is derived from the discount definition formula), then each newly calculated value rk , in turn, is substituted into the formula 
. The sequence of approximations is carried out until the specified accuracy is reached, that is, the discounting factor xk is selected until the condition f (rk) ≤ ε is satisfied, where ε is the specified accuracy (eg, 0.001). The value of rk at which the inequality is fulfilled is the desired internal rate of return IRR .
So, suppose we are given a table in which the data of some investment project are given:
Where:
C - initial investment (the value is always negative);
Vj - financial income from the project in the j-th period;
j is the sequence number of the period (calendar year).
Also, we are given the annual percentage discount rate - i .
We need to determine the internal rate of return of this project - IRR .
The internal rate of return is calculated as follows: you need to choose the value of the interest rate IRR , so that the equation is solved:
In our case, the initial investment (investment) in the project was made only once, according to a given table - in the zero year, respectively, the above equation will take the following form:
To determine the internal rate of return, you still need a formula for determining the total net present value ( NPV ) for five periods of financial income:
Where PVj is the reduced income for the j-th period:
If replaced by the expression
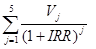expression in the formula for determining the reduced income PV , which is then substituted into the formula for determining the total net present income of NPV , then we obtain the following function:If we replace the desired value of IRR at which
the value of the interest rate r which varies in the interval from 0 to 100%, then we get the function:the graph of which is presented in the figure below:
The graph shows that the task of finding the internal rate of return IRR (NPV (IRR) = 0) is reduced to finding the intersection point of the graph with the x -axis, which can be found using any of the numerical methods.
Take, for example, Newton's numerical method . Having the data, from the given table, let's make a power function of one variable x for the investment project:
The sequence of approximation to the value of the discount multiplier is constructed from the initial value x0 = 1 by the following formula:
Where:
k is the iteration step number;
- derivative of power function:Each newly calculated xk value is substituted into the formula
(this formula is derived from the discount definition formula), then each newly calculated value rk , in turn, is substituted into the formula . The sequence of approximations is carried out until the specified accuracy is reached, that is, the discounting factor xk is selected until the condition f (rk) ≤ ε is satisfied, where ε is the specified accuracy (eg, 0.001). The value of rk at which the inequality is fulfilled is the desired internal rate of return IRR .')
Source: https://habr.com/ru/post/267879/
All Articles