Binary search trees and recursion are just
There are many books and articles on this topic. In this article I will try to clearly explain the most basic.
A binary tree is a hierarchical data structure in which each node has a value (it is also a key in this case) and references to the left and right descendant. A node at the topmost level (which is not a descendant of anyone) is called a root. Nodes that have no descendants (both descendants of which are NULL) are called leaves.
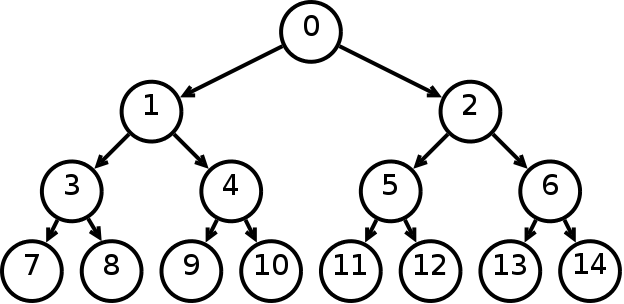
Fig. 1 Binary tree
A binary search tree is a binary tree with additional properties: the value of the left child is less than the value of the parent, and the value of the right child is greater than the value of the parent for each node of the tree. That is, data in a binary search tree is stored in sorted form. Each time you insert a new or delete an existing node, the sorted order of the tree is preserved. When searching for an element, the sought value is compared with the root. If the desired is greater than the root, then the search continues in the right descendant of the root; if less, then in the left, if equal, then the value is found and the search is terminated.
')

Fig. 2 Binary search tree
A balanced binary search tree is a binary search tree with logarithmic height. This definition is more ideological than strict. Strict definition operates with the difference of the depth of the deepest and shallowest leaf (in AVL trees) or the ratio of the depth of the deepest and shallowest leaf (in red-black trees). In a balanced binary search tree, search, insert and delete operations are performed in logarithmic time (since the path to any sheet from the root is no more than a logarithm). In the degenerate case of an unbalanced binary search tree, for example, when a sorted sequence was inserted into an empty tree, the tree would turn into a linear list, and the search, insert and delete operations would be performed in linear time. Therefore, balancing a tree is extremely important. Technically, balancing is performed by turning parts of the tree when inserting a new element, if the insertion of this element violated the balance condition.
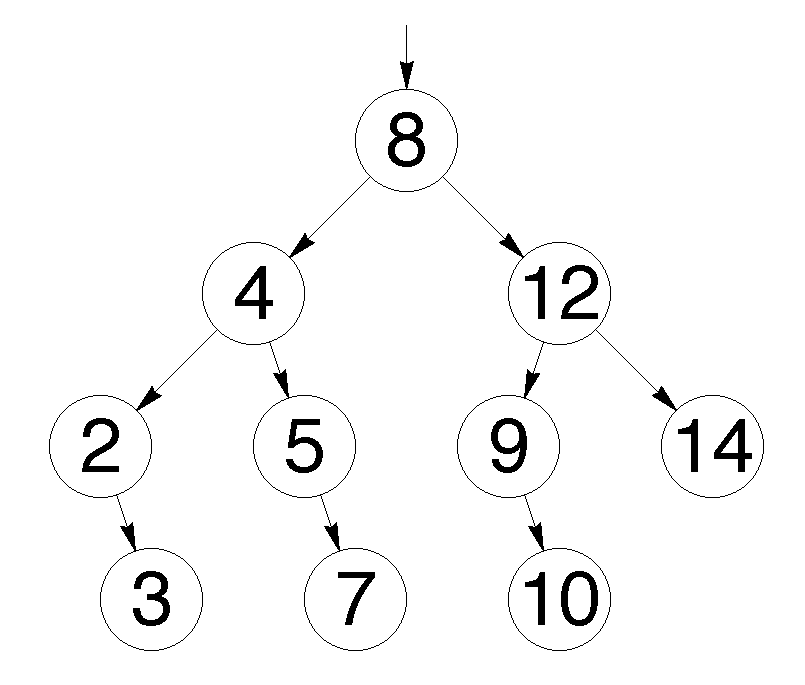
Fig. 3 Balanced Binary Search Tree
A balanced binary search tree is used when you need to quickly search for items, alternating with inserts of new items and deletions of existing ones. If the set of elements stored in the data structure is fixed and there are no new inserts and deletions, then the array is preferable. Because the search can be performed by a binary search algorithm for the same logarithmic time, but there are no additional costs for storing and using pointers. For example, in C ++, the associative containers set and map are a balanced binary search tree.
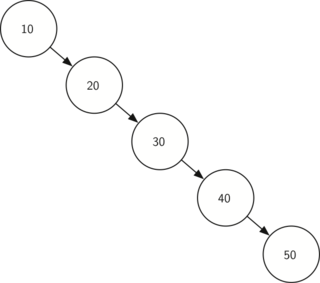
Fig. 4 Extremely unbalanced binary search tree
Now briefly discuss recursion. Recursion in programming is a function call to itself with other arguments. In principle, a recursive function can call itself with the same arguments, but in this case there will be an infinite recursion cycle that will result in a stack overflow. Inside any recursive function, there must be a base case in which the function exits, as well as a call or calls to itself with other arguments. Arguments should not just be different, but should bring the function call to the base case. For example, the call inside the recursive function of calculating factorial should come with a smaller argument, and calls within the recursive tree walk function should go with nodes farther from the root closer to the leaves. Recursion can be not only direct (direct call itself), but also indirect. For example, A calls B, and B calls A. Using recursion, you can emulate an iterative loop as well as the operation of a stack data structure (LIFO).
Let's briefly discuss trees from the point of view of graph theory. A graph is a set of vertices and edges. An edge is a connection between two vertices. The number of possible edges in a graph is quadratically dependent on the number of vertices (for understanding, you can submit a standings of played matches). A tree is a connected graph without cycles. Connectivity means that from any vertex to any other there is a path along the edges. The absence of cycles means that this path is the only one. Traversing a graph is a systematic visit to all its vertices once each. There are two types of traversal graph: 1) search in depth; 2) search wide.
The search in width (BFS) goes from the initial vertex, first visits all the vertices located at a distance of one edge from the initial one, then visits all the vertices at a distance of two edges from the initial one, and so on. The width search algorithm is non-recursive (iterative) in nature. For its implementation, the queue data structure (FIFO) is used.
Depth-first search (DFS) goes from the initial vertex, visiting not yet visited vertices without regard for the distance from the initial vertex. The depth-first search algorithm is recursive in nature. To emulate recursion in an iterative version of the algorithm, the stack data structure is used.
From a formal point of view, it is possible to make both a recursive and an iterative version of both search in width and search in depth. To bypass the width in both cases, a queue is needed. Recursion in a recursive wide bypass implementation only emulates a loop. To crawl into depth, there is a recursive implementation without a stack, a recursive implementation with a stack, and an iterative implementation with a stack. Iterative implementation of a detour in depth without a stack is impossible.
The asymptotic complexity of traversal is both in width and in depth O (V + E), where V is the number of vertices, E is the number of edges. That is, it is linear in the number of vertices and edges. From the substantive point of view, the O (V + E) record is equivalent to the O (max (V, E)) record, but the latter is not accepted. That is, the complexity will be determined by the maximum of two values. Despite the fact that the number of edges depends quadratically on the number of vertices, we cannot write the complexity as O (E), since if the graph is highly sparse, this will be an error.
DFS is used in the algorithm for finding strong connected components in a directed graph. BFS is used to find the shortest path in the graph, in the algorithms for sending messages over the network, in garbage collectors, in the indexing program - in the search engine spider. Both DFS and BFS are used in the algorithm for the search for the minimum spanning tree, when checking cycles in a graph, to check for duplicity.
A width walk in the graph corresponds to a walk through the levels of a binary tree. With this bypass, there is a visit to the nodes on the principle from top to bottom and from left to right. Three types of binary tree traversal correspond to depth traversal in a graph: direct (pre-order), symmetrical (in-order) and reverse (post-order).
The direct round goes in the following order: root, left descendant, right descendant. Symmetrical - left descendant, root, right descendant. Reverse - left descendant, right descendant, root. In the code of the recursive function of the corresponding traversal, the corresponding order of calls is retained (the order of the lines of code), where instead of the root there is a call of the given recursive function.
If we are given an image of a tree, and we need to find its rounds, then the following technique can help (see. Fig. 5). We circle the tree of the envelope of a closed curve (we start to go left down and close right up). Direct traversal will correspond to the order in which the envelope, moving from the root for the first time, passes next to the nodes to the left. For symmetric traversal, the order in which the envelope, moving from the root for the first time, passes next to the nodes below. For the reverse traversal, the order in which the envelope, moving from the root, first passes next to the nodes to the right. In the code of the recursive call, the direct bypass goes: call, left, right. Symmetric - left, call, right. Reverse - left right, call.

Fig. 5 Auxiliary pattern for crawling
For binary search trees, symmetric traversal traverses all nodes in sorted order. If we want to visit the nodes in reverse sorted order, then in the code of the recursive function of the symmetric traversal, we should swap the left and right children.
I hope you did not fall asleep, and the article was useful. Soon I hope to follow the continuation of thebanquet of the article.
A binary tree is a hierarchical data structure in which each node has a value (it is also a key in this case) and references to the left and right descendant. A node at the topmost level (which is not a descendant of anyone) is called a root. Nodes that have no descendants (both descendants of which are NULL) are called leaves.

Fig. 1 Binary tree
A binary search tree is a binary tree with additional properties: the value of the left child is less than the value of the parent, and the value of the right child is greater than the value of the parent for each node of the tree. That is, data in a binary search tree is stored in sorted form. Each time you insert a new or delete an existing node, the sorted order of the tree is preserved. When searching for an element, the sought value is compared with the root. If the desired is greater than the root, then the search continues in the right descendant of the root; if less, then in the left, if equal, then the value is found and the search is terminated.
')

Fig. 2 Binary search tree
A balanced binary search tree is a binary search tree with logarithmic height. This definition is more ideological than strict. Strict definition operates with the difference of the depth of the deepest and shallowest leaf (in AVL trees) or the ratio of the depth of the deepest and shallowest leaf (in red-black trees). In a balanced binary search tree, search, insert and delete operations are performed in logarithmic time (since the path to any sheet from the root is no more than a logarithm). In the degenerate case of an unbalanced binary search tree, for example, when a sorted sequence was inserted into an empty tree, the tree would turn into a linear list, and the search, insert and delete operations would be performed in linear time. Therefore, balancing a tree is extremely important. Technically, balancing is performed by turning parts of the tree when inserting a new element, if the insertion of this element violated the balance condition.

Fig. 3 Balanced Binary Search Tree
A balanced binary search tree is used when you need to quickly search for items, alternating with inserts of new items and deletions of existing ones. If the set of elements stored in the data structure is fixed and there are no new inserts and deletions, then the array is preferable. Because the search can be performed by a binary search algorithm for the same logarithmic time, but there are no additional costs for storing and using pointers. For example, in C ++, the associative containers set and map are a balanced binary search tree.

Fig. 4 Extremely unbalanced binary search tree
Now briefly discuss recursion. Recursion in programming is a function call to itself with other arguments. In principle, a recursive function can call itself with the same arguments, but in this case there will be an infinite recursion cycle that will result in a stack overflow. Inside any recursive function, there must be a base case in which the function exits, as well as a call or calls to itself with other arguments. Arguments should not just be different, but should bring the function call to the base case. For example, the call inside the recursive function of calculating factorial should come with a smaller argument, and calls within the recursive tree walk function should go with nodes farther from the root closer to the leaves. Recursion can be not only direct (direct call itself), but also indirect. For example, A calls B, and B calls A. Using recursion, you can emulate an iterative loop as well as the operation of a stack data structure (LIFO).
int factorial(int n) { if(n <= 1) // { return 1; } return n * factorial(n - 1); // } // factorial(1): return 1 // factorial(2): return 2 * factorial(1) (return 2 * 1) // factorial(3): return 3 * factorial(2) (return 3 * 2 * 1) // factorial(4): return 4 * factorial(3) (return 4 * 3 * 2 * 1) // n (n - int // . long long // . , // // ). void reverseBinary(int n) { if (n == 0) // { return; } cout << n%2; reverseBinary(n/2); // } // void forvardBinary(int n) { if (n == 0) // { return; } forvardBinary(n/2); // cout << n%2; } // // // void ReverseForvardBinary(int n) { if (n == 0) // { return; } cout << n%2; // ReverseForvardBinary(n/2); // cout << n%2; // } // , // int product(int x, int y) { if (y == 0) // { return 0; } return (x + product(x, y-1)); // } // x * y ( xy ) // , // Let's briefly discuss trees from the point of view of graph theory. A graph is a set of vertices and edges. An edge is a connection between two vertices. The number of possible edges in a graph is quadratically dependent on the number of vertices (for understanding, you can submit a standings of played matches). A tree is a connected graph without cycles. Connectivity means that from any vertex to any other there is a path along the edges. The absence of cycles means that this path is the only one. Traversing a graph is a systematic visit to all its vertices once each. There are two types of traversal graph: 1) search in depth; 2) search wide.
The search in width (BFS) goes from the initial vertex, first visits all the vertices located at a distance of one edge from the initial one, then visits all the vertices at a distance of two edges from the initial one, and so on. The width search algorithm is non-recursive (iterative) in nature. For its implementation, the queue data structure (FIFO) is used.
Depth-first search (DFS) goes from the initial vertex, visiting not yet visited vertices without regard for the distance from the initial vertex. The depth-first search algorithm is recursive in nature. To emulate recursion in an iterative version of the algorithm, the stack data structure is used.
From a formal point of view, it is possible to make both a recursive and an iterative version of both search in width and search in depth. To bypass the width in both cases, a queue is needed. Recursion in a recursive wide bypass implementation only emulates a loop. To crawl into depth, there is a recursive implementation without a stack, a recursive implementation with a stack, and an iterative implementation with a stack. Iterative implementation of a detour in depth without a stack is impossible.
The asymptotic complexity of traversal is both in width and in depth O (V + E), where V is the number of vertices, E is the number of edges. That is, it is linear in the number of vertices and edges. From the substantive point of view, the O (V + E) record is equivalent to the O (max (V, E)) record, but the latter is not accepted. That is, the complexity will be determined by the maximum of two values. Despite the fact that the number of edges depends quadratically on the number of vertices, we cannot write the complexity as O (E), since if the graph is highly sparse, this will be an error.
DFS is used in the algorithm for finding strong connected components in a directed graph. BFS is used to find the shortest path in the graph, in the algorithms for sending messages over the network, in garbage collectors, in the indexing program - in the search engine spider. Both DFS and BFS are used in the algorithm for the search for the minimum spanning tree, when checking cycles in a graph, to check for duplicity.
A width walk in the graph corresponds to a walk through the levels of a binary tree. With this bypass, there is a visit to the nodes on the principle from top to bottom and from left to right. Three types of binary tree traversal correspond to depth traversal in a graph: direct (pre-order), symmetrical (in-order) and reverse (post-order).
The direct round goes in the following order: root, left descendant, right descendant. Symmetrical - left descendant, root, right descendant. Reverse - left descendant, right descendant, root. In the code of the recursive function of the corresponding traversal, the corresponding order of calls is retained (the order of the lines of code), where instead of the root there is a call of the given recursive function.
If we are given an image of a tree, and we need to find its rounds, then the following technique can help (see. Fig. 5). We circle the tree of the envelope of a closed curve (we start to go left down and close right up). Direct traversal will correspond to the order in which the envelope, moving from the root for the first time, passes next to the nodes to the left. For symmetric traversal, the order in which the envelope, moving from the root for the first time, passes next to the nodes below. For the reverse traversal, the order in which the envelope, moving from the root, first passes next to the nodes to the right. In the code of the recursive call, the direct bypass goes: call, left, right. Symmetric - left, call, right. Reverse - left right, call.

Fig. 5 Auxiliary pattern for crawling
For binary search trees, symmetric traversal traverses all nodes in sorted order. If we want to visit the nodes in reverse sorted order, then in the code of the recursive function of the symmetric traversal, we should swap the left and right children.
struct TreeNode { double data; // / TreeNode *left; // TreeNode *right; // }; void levelOrderPrint(TreeNode *root) { if (root == NULL) { return; } queue<TreeNode *> q; // q.push(root); // while (!q.empty() ) // { TreeNode* temp = q.front(); // q.pop(); // cout << temp->data << " "; // if ( temp->left != NULL ) q.push(temp->left); // if ( temp->right != NULL ) q.push(temp->right); // } } void preorderPrint(TreeNode *root) { if (root == NULL) // { return; } cout << root->data << " "; preorderPrint(root->left); // preorderPrint(root->right); // } // . // // void inorderPrint(TreeNode *root) { if (root == NULL) // { return; } preorderPrint(root->left); // cout << root->data << " "; preorderPrint(root->right); // } // . // void postorderPrint(TreeNode *root) { if (root == NULL) // { return; } preorderPrint(root->left); // preorderPrint(root->right); // cout << root->data << " "; } // . // ( ). void reverseInorderPrint(TreeNode *root) { if (root == NULL) // { return; } preorderPrint(root->right); // cout << root->data << " "; preorderPrint(root->left); // } // . // void iterativePreorder(TreeNode *root) { if (root == NULL) { return; } stack<TreeNode *> s; // s.push(root); // /* . 1) 2) ! (! !) 3) ! */ while (s.empty() == false) { // TreeNode *temp = s.top(); s.pop(); cout << temp->data << " "; if (temp->right) s.push(temp->right); // if (temp->left) s.push(temp->left); // } } // // . I hope you did not fall asleep, and the article was useful. Soon I hope to follow the continuation of the
Source: https://habr.com/ru/post/267855/
All Articles