Candy Challenge
The other day I ran into an interesting puzzle, which seemed to me a decent audience for this resource. The condition is as follows:
“Find the maximum permissible deviation of the mass of candy during its production, so that the net of a box consisting of 12 pieces of them does not exceed 310 ± 7 grams in 90% of cases. The distribution law is considered normal. "
It should be said that the condition was not pulled out of the Internet or overlooked on any resource of entertaining tasks, but came from a very good friend who is an engineer in production organization and production management at a well-known confectionery factory. That is, the task has a very real origin, and its solution has practical benefits.
')
I suggested that readers solve the problem on their own and should say that they did it better than me. In my own decision, I made the wrong assumption.
Let's agree to designate in big letters the parameters for the box and small ones for the candies.
Let him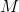 and
and  - respectively, the net weight of the box and its tolerance, such that
- respectively, the net weight of the box and its tolerance, such that 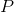 percent of cases it does not go beyond
percent of cases it does not go beyond 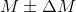 .
.
Let him and
and 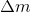 - respectively, the mass of candy and its tolerance, such that
- respectively, the mass of candy and its tolerance, such that  percent of cases it does not go beyond
percent of cases it does not go beyond 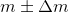 .
.
The number of candies in the box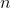 .
.
The normal distribution is described by the Gauss function:
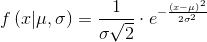
where - expected value,
- expected value, 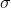 - standard deviation whose square
- standard deviation whose square 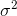 - called dispersion.
- called dispersion.
In the case of candy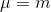 a
a 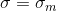 , so:
, so:
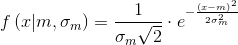
In the case of a box of chocolates a
a 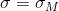 :
:
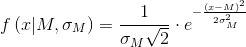
Probability the fact that the mass of candy will not go beyond
the fact that the mass of candy will not go beyond 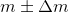 equals:
equals:
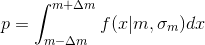
Probability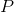 the fact that the net box will not go beyond
the fact that the net box will not go beyond 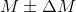 equals:
equals:
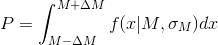
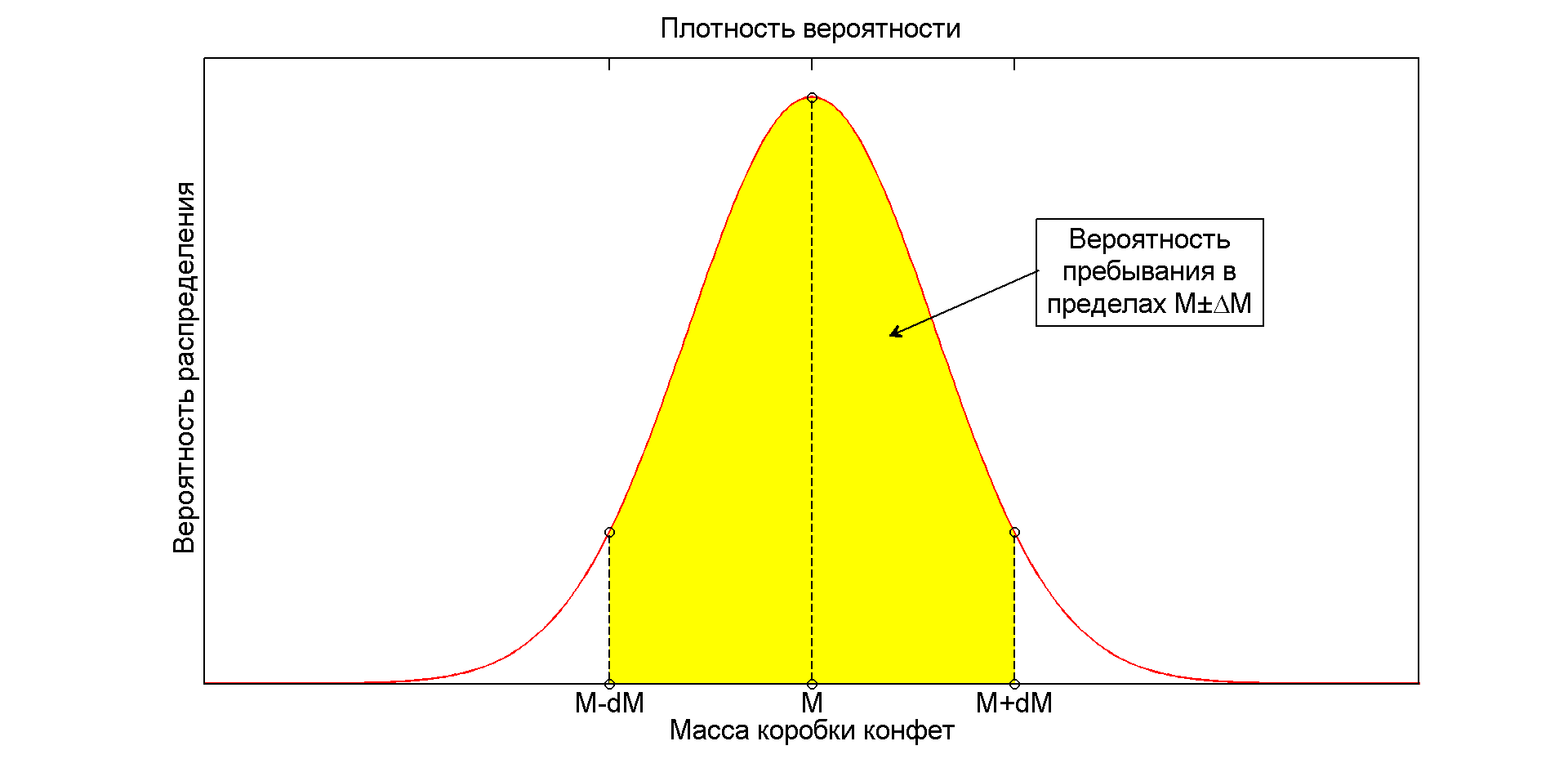
The figure below illustrates all of the above:
Find the probability for the candy:
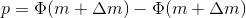
where - distribution function, and
- distribution function, and 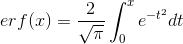 - error function.
- error function.
Thus for candy:
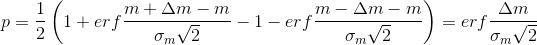
Similarly for the box:
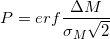
From the central limit theorem, it follows that if there are independent random variables:

, their sum is:
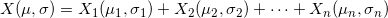
will have the parameters:
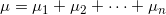
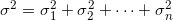
In relation to our situation, we have:
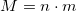

I mistakenly thought that the cumulative probability for a box is equal to the product of probabilities for individual candies. In other words:
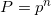
from where
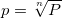
The result was a system of equations:
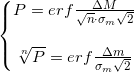
Deciding her relatively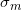 :
:
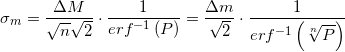
brought:
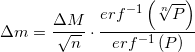
where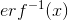 - the inverse function of errors and found quite specific numbers:
- the inverse function of errors and found quite specific numbers:
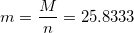
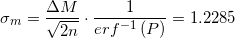
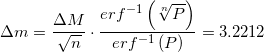
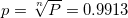
I justified such a decision as follows: it is necessary that the mass of candy does not go beyond 25.8333 ± 3.2212 in 99.13% of cases (1 to 115). And although this answer is not contradictory, the truth is that only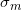 is the right answer. Since with such a smaller standard deviation, we do not need to discard anything, which many readers hinted to me for a long time and were right.
is the right answer. Since with such a smaller standard deviation, we do not need to discard anything, which many readers hinted to me for a long time and were right.
As without her. Checkout cooked up in the lab. In short, we create 1000000 sweets with the found parameters according to the normal law. In a random (equiprobable) way, we form 1,000,000 groups of them (count boxes) of 12 pieces of them. We check the number of such groups that did not go beyond 310 ± 7 and divide by the total, thus obtaining the same probability for the box. And so 1000 times.
The result was such a beautiful schedule:
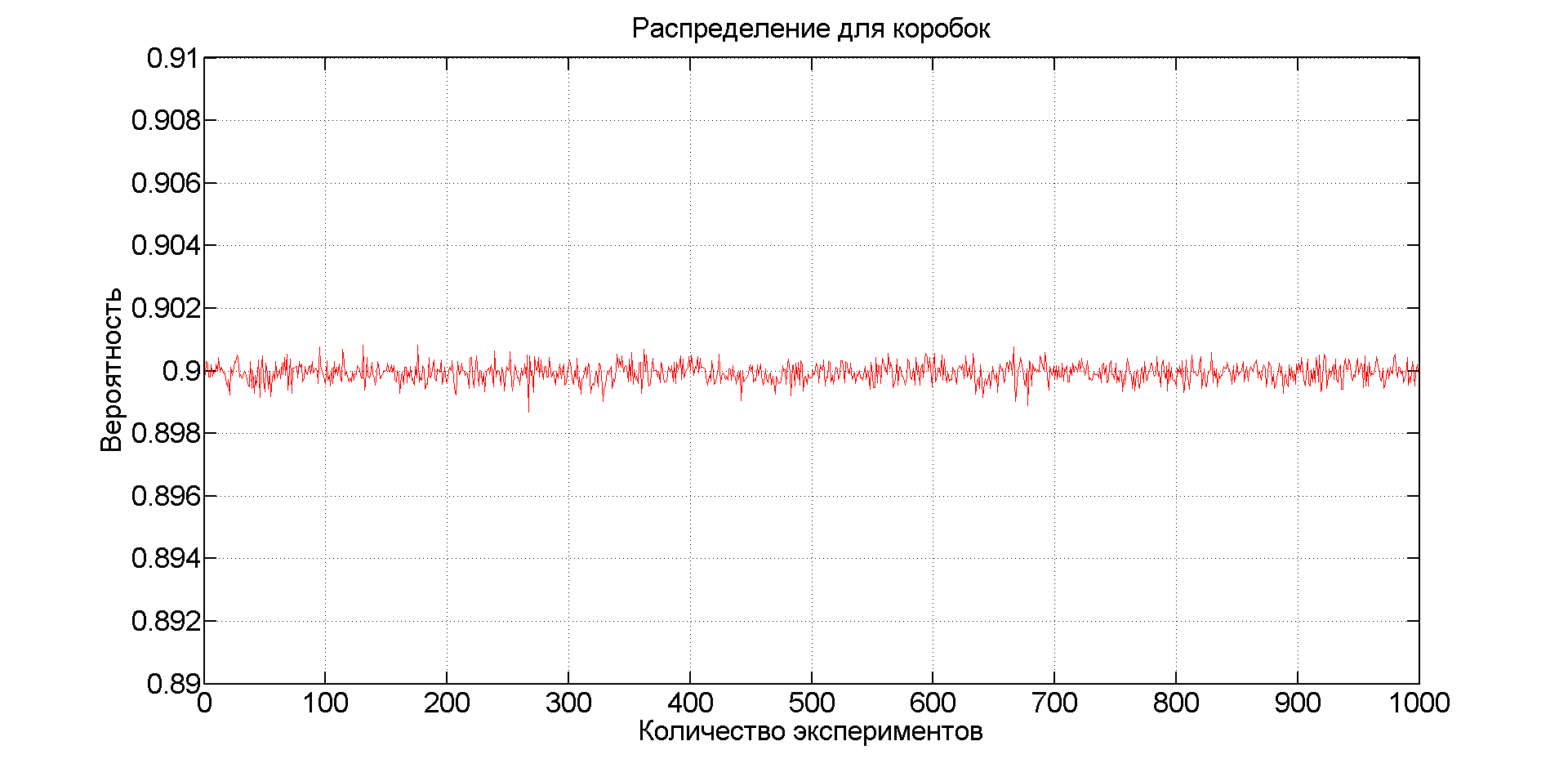
I dare to suggest that 1 million boxes are few and if we rush them to infinity, our probabilities will be exactly 90%.
Much more interesting is the case when the candy dispenser has a constant standard deviation, which is more than 1.2285 and you need to find the same boundaries.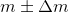 , above which, given
, above which, given 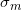 Candy must be discarded to meet the same conditions. This is a much more difficult task, to which I may devote another article.
Candy must be discarded to meet the same conditions. This is a much more difficult task, to which I may devote another article.
“Find the maximum permissible deviation of the mass of candy during its production, so that the net of a box consisting of 12 pieces of them does not exceed 310 ± 7 grams in 90% of cases. The distribution law is considered normal. "
It should be said that the condition was not pulled out of the Internet or overlooked on any resource of entertaining tasks, but came from a very good friend who is an engineer in production organization and production management at a well-known confectionery factory. That is, the task has a very real origin, and its solution has practical benefits.
')
I suggested that readers solve the problem on their own and should say that they did it better than me. In my own decision, I made the wrong assumption.
1. Conventions
Let's agree to designate in big letters the parameters for the box and small ones for the candies.
Let him
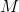 and
and  - respectively, the net weight of the box and its tolerance, such that
- respectively, the net weight of the box and its tolerance, such that 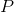 percent of cases it does not go beyond
percent of cases it does not go beyond 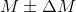 .
.Let him
 and
and 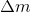 - respectively, the mass of candy and its tolerance, such that
- respectively, the mass of candy and its tolerance, such that 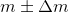 .
.The number of candies in the box
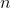 .
.2. Normal distribution
The normal distribution is described by the Gauss function:
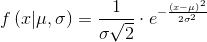
where
 - expected value,
- expected value, 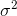 - called dispersion.
- called dispersion.In the case of candy
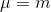 a
a 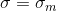 , so:
, so: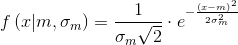
In the case of a box of chocolates
 a
a 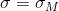 :
: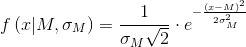
Probability
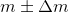 equals:
equals: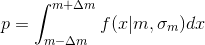
Probability
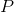 the fact that the net box will not go beyond
the fact that the net box will not go beyond 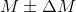 equals:
equals: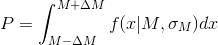
The figure below illustrates all of the above:

Find the probability for the candy:
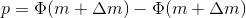
where
 - distribution function, and
- distribution function, and 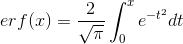 - error function.
- error function.Thus for candy:
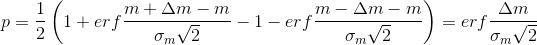
Similarly for the box:
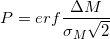
3. Central limit theorem
From the central limit theorem, it follows that if there are independent random variables:

, their sum is:
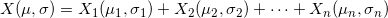
will have the parameters:
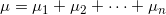
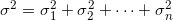
In relation to our situation, we have:
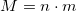

4. Probabilities and my mistake
I mistakenly thought that the cumulative probability for a box is equal to the product of probabilities for individual candies. In other words:
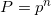
from where
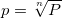
The result was a system of equations:
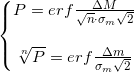
Deciding her relatively
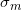 :
: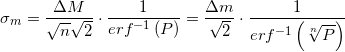
brought:
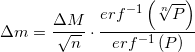
where
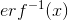 - the inverse function of errors and found quite specific numbers:
- the inverse function of errors and found quite specific numbers: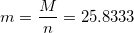
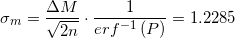
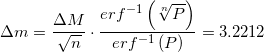
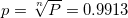
I justified such a decision as follows: it is necessary that the mass of candy does not go beyond 25.8333 ± 3.2212 in 99.13% of cases (1 to 115). And although this answer is not contradictory, the truth is that only
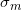 is the right answer. Since with such a smaller standard deviation, we do not need to discard anything, which many readers hinted to me for a long time and were right.
is the right answer. Since with such a smaller standard deviation, we do not need to discard anything, which many readers hinted to me for a long time and were right.5. Verification
As without her. Checkout cooked up in the lab. In short, we create 1000000 sweets with the found parameters according to the normal law. In a random (equiprobable) way, we form 1,000,000 groups of them (count boxes) of 12 pieces of them. We check the number of such groups that did not go beyond 310 ± 7 and divide by the total, thus obtaining the same probability for the box. And so 1000 times.
Code
% Number of candys nC = 1000000 ; % Mass deviation of a single candy mC = normrnd ( m , s , 1 , nC ) ; % Number of candys in the box n = 12 ; % Number of boxes nB = 1000000 ; % Number of experiments nE = 1000; pB = zeros ( 1, nE ); for k = 1 : nE % Random index of n candys i = random ( 'unid' , nC , nB, n ) ; % The mass of each boxes j = 1 : nB ; mB = sum ( mC ( i ( j , : ) ) , 2 )' ; % Mask boxes that out of range mask = ( mB < M + dM ) .* ( mB > M - dM ); % Probability of out of the range pB ( k ) = sum ( mask ) / nB; end The result was such a beautiful schedule:

I dare to suggest that 1 million boxes are few and if we rush them to infinity, our probabilities will be exactly 90%.
Much more interesting is the case when the candy dispenser has a constant standard deviation, which is more than 1.2285 and you need to find the same boundaries.
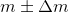 , above which, given
, above which, given 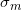 Candy must be discarded to meet the same conditions. This is a much more difficult task, to which I may devote another article.
Candy must be discarded to meet the same conditions. This is a much more difficult task, to which I may devote another article.Source: https://habr.com/ru/post/267777/
All Articles